Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
No, no se puede utilizar un rastreador para evaluar cuánto ha cambiado el mercado.
Sólo se puede evaluar en qué medida los nuevos errores de predicción han modificado la previsión con respecto a los antiguos errores.
Es decir, SSA no dice nada sobre la corrección de la previsión, la diferencia de SSA sólo nos habla de la diferencia de errores. A dónde irá el mercado, a la SSA no le importa en absoluto.
Sin la estimación del error de cada SSA, su diferencia queda en el aire, no tiene nada en qué basarse.
Lo sé desde hace mucho tiempo, pero tengo esperanza, así que estoy pensando dónde buscar :)) Quiero correr la matriz de covarianza en la historia y analizar cuán grandes son las diferencias en ella - y de repente dicen en teoría que el precio tiene en cuenta todo y así ))))
No sé, me parece que si Alejandro no ha llegado hasta el final, nada puede salvar este planteamiento. Predecir el vagabundeo aleatorio es difícil, y evaluarlo algunos estados imaginarios :)
Aquí, además de mi post anterior, sobre todo la parte anecdótica... En SSA tendré tiempo, haré un conjunto de todas las posibles matrices de covarianza y trataré de analizarlas para que no se repitan en estados cercanos, es decir, las matrices deben alternarse en orden no repetitivo
tal vez en la noche voy a limpiar el código por SSA y publicarlo, el código es sólo un puerto de Matlab, no esperaba, pero Alglib es muy útil para portar rápidamente este tipo de cosas hizo como un ejemplo a mí mismo con el fin de aprender, también puede ayudar a alguien a entender, aquí está Matlab SSA adjunto
Destacaré la pregunta por separado:
¿Sobre qué función hacer una regresión para que su último punto esté en el centro del canal de precios?
Necesito una función, como un polinomio, que pueda manejar tanto el zigzag como la media circunferencia (como puedes ver en los ejemplos, el polinomio no puede manejar estos temas).
(La figura de Maxim Dmitrievsky no puede ser considerada todavía, no se ajusta a la teoría de que el precio es un canal de trading que sigue una trayectoria determinada. esta figura es un canal de trading con una eyección al final, puede ser considerada más adelante).
Otros ejemplos de funciones no lineales son las funciones exponenciales, las funciones logarítmicas, las funciones trigonométricas, las funciones de potencia, las funciones gaussianas y las curvas de Lorenz.
Bueno Smokchy, ¡tienes a todo el mundo alborotado con tus fotos! ))
Bueno y un poco de psicología para evaluar si la búsqueda del Grial es exitosa, disfruté el video, aparentemente la chica se ve natural y convincente
Y un poco de psicología para calibrar si la búsqueda del Grial tiene éxito, me ha gustado el vídeo, aparentemente la chica parece natural y convincente
Podrías dar a luz a una oruga por la noche con esos ojos.
un poco de psicología para medir el éxito de la búsqueda del Grial, me gustó el video, aparentemente la chica se ve natural y convincente
La chica es inteligente-joven ve lo invisible para muchos.
Bueno, si la psicología es interesante, la guinda del pastel...
bueno, si la psicología es interesante, la guinda del pastel, por así decirlo...
El minuto 30 de la película es el más interesante), pero hay que verla entera para entenderla.
Ya te han dicho que es un pasatiempo inútil.
hasta que no has pasado tu tiempo, no lo entiendes.
Cómo hacer una regresión en Excel.
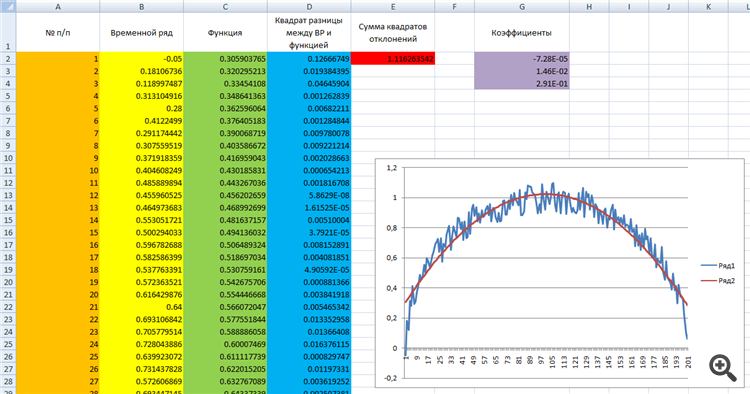
Utilizar la función de búsqueda de datos/soluciones.
En la tabla adjunta:
la primera columna es el número de la n/a.
la segunda columna es la serie temporal.
La tercera es una función (en este caso, un polinomio).
El cuarto es el CNA. el valor de la serie temporal menos el valor de la función, y al cuadrado.
en las celdas rojas es la suma sobre la columna azul, es decir, la suma de los cuadrados de las desviaciones.
en las celdas de color púrpura son los coeficientes que hay que ajustar.
La función polinómica es y=ax2+bx+c
donde x es el valor de las coordenadas en el eje x. columna naranja. de 0 a 201.
y son los valores de las coordenadas en el eje y que tendrá el polinomio elegido.
a,b,c son los coeficientes que vamos a ajustar.
En Excel, la fórmula se verá así =a*A1^2+b*A1+c. Es decir, sustituimos los valores de la columna A en lugar de las X (véase la columna verde).
Para encontrar los coeficientes de la función, haga clic en "Datos" y luego en "Buscar solución".

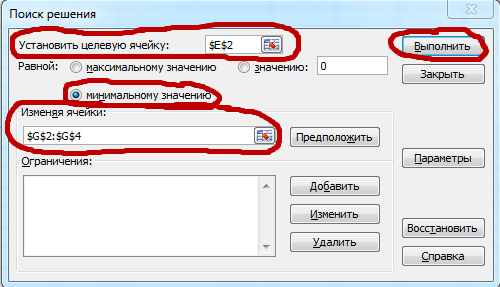
En el menú que se abre seleccione:
Establezca la celda de destino (la celda roja en nuestra tabla),
a un valor mínimo,
Cambiar las celdas (celdas moradas en nuestra tabla).
y luego haga clic en Ejecutar.
Es decir, minimizamos los cuadrados de las desviaciones de las series temporales respecto a la función.
Intenta poner tus propias funciones en la columna verde.
funcionesexponenciales, funciones logarítmicas, funciones trigonométricas, funciones de potencia, función gaussiana, curvas de Lorenz, otras...
El problema sigue siendo el mismo, el último punto de esta función debe estar en el centro del canal de precios (tanto para el zigzag como para el semicírculo).
...
Es decir, minimizamos los cuadrados de las desviaciones de la serie temporal respecto a la función.
Intenta poner tus propias funciones en la columna verde.
funcionesexponenciales, funciones logarítmicas, funciones trigonométricas, funciones de potencia, función gaussiana, curvas de Lorenz, otras...
El problema es el mismo: hay que encontrar una función cuyo último punto esté en el centro del canal de precios (tanto para las figuras en zigzag como para las de medio círculo).
Interesante. En primer lugar, es inexacto, no minimizamos "cuadrados", sino "suma de cuadrados". En segundo lugar, si se quiere dar mayor valor a los últimos puntos, se hace de forma sencilla, en la suma minimizada se toman no sólo cuadrados, sino cuadrados ponderados, que se multiplican por unos coeficientes de ponderación positivos. Sus valores al final de la matriz deben ser mayores, y al principio - menores. Por ejemplo, para números de puntos i de 1 a n, los pesos iguales a q^(n-i) con q < 1, dan multiplicadores de desviación al cuadrado similares a los pesos de los cursos en una media móvil exponencial. A menudo su suma también se hace igual a uno, si queremos comparar diferentes aproximaciones por el valor de la mínima suma ponderada de cuadrados de desviación.
¿Y cuál es el "centro" de un canal curvilíneo cuyos límites se describen con distintos tipos de fórmulas? ¿O al menos para la primera variante, por funciones exponenciales?
Si es simplemente el punto medio del segmento que va desde el penúltimo valor de la serie hasta el último, basta con que los pesos de la desviación en los dos últimos puntos de la serie sean muy grandes. O más sencillo aún, encontrar este medio y ya está.
Se necesitan otros requisitos para las desviaciones, de lo contrario se subestima el problema.
¿De qué sirve calcular el "centro" en el último punto?