Valores óptimos de las órdenes SL y TP para una TS arbitraria. - página 14
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Вот я и думаю, что постановка задачи в самом начале является узкой, в самом узком смысле этого слова. Сдается мне, что это никакого отношения к общему случаю не имеет. :о( Но возможно - ошибаюсь.
¡Bueno, querida! Estoy luchando por unirlo todo, mientras tú intentas ampliar el marco para mí :-)
Adelante, elige la postura más amplia y muéstranos cómo se hace. Aprenderemos. Mientras tanto, haremos lo que podamos.
Sigamos considerando el paso de una ST ideal con distribución de TP en forma de delta y que se encuentra en el óptimo de la doble extensión (fig. de la izquierda, en rojo) a la óptima: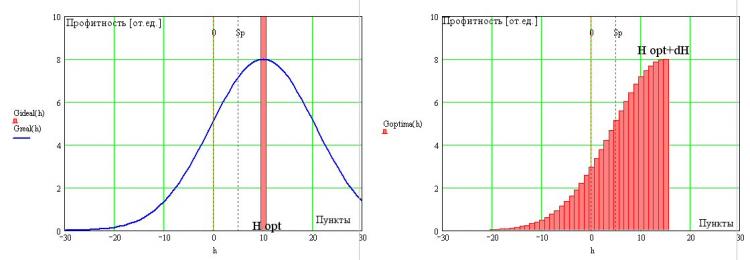
Por supuesto, hay que admitir que en la realidad, sin una oportunidad de mirar hacia el futuro (estando en el lado correcto de la BP), tenemos que aguantar los errores del funcionamiento óptimo del TP que son inevitables debido a la ausencia de milagros en la Naturaleza (ya se mencionó especialmente). En consecuencia, el FS de la TS óptima tendrá una dilución de la distribución delta-funcional de su prototipo ideal, como se muestra en la misma figura con la línea azul.
Debido al hecho de que todas las posiciones abiertas comienzan automáticamente con un valor negativo en -Sp, incluso para la TS óptima tendremos definitivamente transacciones con un resultado negativo. Además, las propias operaciones pueden cerrarse con cualquier gran menos (omitiremos el trabajo con órdenes de protección por el momento). Es una condición inevitable de la realidad. Pero podemos cambiar la forma para el borde derecho y tenemos un cierto grado de libertad. Esto se debe, obviamente, a que podemos elegir cuándo cerrar una operación rentable. Teniendo en cuenta que existe un óptimo para el valor del beneficio H, podemos suponer que existe un borde afilado en el lado derecho del TP del óptimo TS. Este requisito se debe, como ya he señalado, a la existencia de dos procesos que compiten entre sí y que afectan a la rentabilidad de la CT: la frecuencia de las transacciones y su amplitud. Por lo tanto, el límite de la derecha ciertamente existirá, pero ¿coincidirá con Н opt, como para la TS ideal. Obviamente no. Y esto se debe a la presencia de la inevitable cola apretada de la izquierda. En el caso más general, el límite derecho de FR estará en la zona detrás de Н opt (ver fig. a la derecha) y su ubicación exacta no es importante para nosotros en esta etapa de nuestro razonamiento.
De este modo, se obtiene la visión general del modelo de distribución de tomas de la ST óptima. Tendrá necesariamente un borde derecho empinado, cuya ubicación exacta está determinada por la extensión Sp y un ala derecha monótonamente decreciente con una entrada obligatoria en la zona negativa. La forma exacta de esta ala se reconstruirá más adelante. Pero ya podemos decir que la planitud (o inclinación) de la pendiente izquierda está determinada por la ausencia o presencia (su fuerza) de regularidades en la serie inicial de precios y la integral de esta montaña debería (según t. Oak) dar el cero exacto en la martingala, lo que nos permitirá después encontrar su (TS) algunas características.
ystr escribió(a) >> Si tenemos en cuenta que "para una ST ideal todas las direcciones son adivinables" entonces debo señalar que tal sistema es difícil de implementar en la práctica. Y si establecemos la condición de que "el rango de cambios de precios" esté dentro del spread, entonces es imposible.
Claro que sí. Ya lo he mencionado anteriormente.
все верно. Но плановый TP зависит от временного горизонта во многом.
Definitivamente. Simplemente no estoy de acuerdo con SL. A pesar de la ventaja de las estadísticas, no se excluyen en absoluto los picos contra nosotros, incluidos los fuertes. Hay que reducir la cuota de capital en el juego, o protegerse de la demanda de márgenes por la parada. Por lo tanto, hay un tema de optimización.
...
мы вправе предположить наличие резкой границы справа у ФР взяток оптимальной ТС. Это требование связано, как я уже отмечал, с наличием двух конкурирующих процессов влияющих на профитность ТС - частоты совершения транзакций и их амплитуды.
Me resulta difícil estar de acuerdo aquí, al menos sobre la marcha. De hecho, aquí se habla de alguna forma de cierre forzoso de la posición en función del tiempo. Este cierre no daría un corte abrupto, sino una supresión gradual de las colas.
Bien, el recorte abrupto puede considerarse una aproximación a esta supresión. Pero el tiempo aplastará ambas colas, porque las grandes pérdidas también están asociadas al tiempo, así como los grandes beneficios.
Definitivamente. Simplemente no estoy de acuerdo con SL. A pesar de la ventaja de las estadísticas, no se excluyen en absoluto los picos contra nosotros, incluidos los fuertes. Hay que reducir la cuota de capital en el juego, o protegerse de la demanda de márgenes por la parada. Ese es el tema de la optimización.
Depende de cuál de las 3 variantes. Cuando la longitud de la serie se conoce de antemano, entonces es eficiente seleccionar el tamaño de la estaca - en función de la longitud de la serie y sin utilizar SL. Si no se conoce la longitud de la serie, el SL tiene sentido, y el tamaño del lote se seleccionará según su valor. O viceversa - tamaño de la oferta - selección de SL. Es decir, sólo en combinación con la oferta de tamaño-SL.
Pero estos son ejemplos abstractos, en la práctica el SL es necesario, porque la distribución real de los precios no es estacionaria y en lugar de una ventaja estadística después de entrar es posible obtener una pérdida estadística en algún momento/después de algún evento. Eso es lo que SL está tratando de cortar.
Neutron писал(а) >>
Así que adelante, elige tu puesta en escena más amplia y muéstranos cómo se hace. Aprenderemos. Mientras tanto, haremos lo que podamos.
El tema de SL me interesa mucho, y sigue abierto, por lo que te he estado molestando con preguntas. La gravitación de la fuerza gravitacional está determinada por la cantidad de mercurio en las dos primeras semanas, pero no aumenta el valor de la gravitación. Y, por supuesto, espero que se convierta en algo común en el sentido estricto de la palabra. :о)
Depende de cuál de las 3 opciones. Cuando la longitud de la serie se conoce de antemano, el método de selección del tamaño de la estaca es eficaz, de nuevo, en función de la longitud de la serie y sin utilizar el SL. Si no se conoce la longitud de la serie, el SL tiene un significado y el lote se seleccionará en función de su tamaño. O viceversa - tamaño de la oferta - selección de SL. Es decir, sólo en combinación con la oferta de tamaño-SL.
Pero estos son ejemplos abstractos, en la práctica el SL es necesario, porque la distribución real de los precios no es estacionaria y en lugar de una ventaja estadística después de entrar es posible obtener una pérdida estadística en algún momento/después de algún evento. Eso es lo que SL está tratando de cortar.
Y en mi opinión, cuando se conoce la longitud de la serie, es conveniente elegir el SL para ella en base a la estadística, en función de la medida de riesgo aceptada por uno mismo. Salirse de esta medida se percibe como un gran pico repentino contra la posición y es cerrado por el SL.
Y en mi opinión, cuando se conoce la duración de la serie, es conveniente elegir el SL para ella en base a la estadística, en función de la medida de riesgo aceptada por uno mismo. Superar esta medida se percibe como un pico inesperado contra la posición y se cierra por SL.
Así es en las tareas reales. Lo que describí fue para una moneda con probabilidades constantes
Но существует и вторая ось координатной плоскости, где разыгрываются наши события, - ценовая, и связь между ними однозначная. Согласно выше приведённой формуде, амплитуда цены V(t) и время t в течении которого эта амплитуда наигрывается связаны следующим выражением:
La suposición de una relación de uno a uno parece poco razonable; en realidad, la relación es estadística. Pero incluso en la aproximación de la relación inequívoca, esta fórmula se aplicará tanto a las mociones "a favor" como a las "en contra".
Por lo tanto, imho, la asimetría puede ser correctamente introducido sólo mediante la introducción de condiciones adicionales. Por ejemplo, en este caso sería "recortar el beneficio, dejar que la pérdida crezca". En general, para una consideración separada de la SL se puede entrar también por este lado, pero hay que estipularlo. Por supuesto.
Предположение об однозначности связи выглядит неоправданно сильным, реально эта связь статистическая. Но даже в приближении однозначной связи эта формула будет относиться как к движениям "за нас", так и к движениям "против нас".
Поэтому, имхо, корректно ввести асимметрию можно только введя дополнительные условия. Например для данного случая это будет "режь прибыль, давай убытку расти". В общем для отдельного рассмотрения вопроса о SL можно зайти и с этой стороны, но это нужно оговорить. Имхо, разумеется.
No sé... No se me ocurre nada en este momento.
Volvamos al análisis de la FC óptima (OTS, porque estoy harto de escribir lo mismo :-).
En la fig. se ve que tenemos dos grados de libertad para determinar la posición del FS - se puede mover a la izquierda - derecha y cambiar la inclinación de la pendiente (fig. a la izquierda):
Además, las dependencias de cambio de pendiente en las series de precios son las responsables. Dado que sólo hay dos opciones (steeper-posher), podemos suponer que estas dos opciones corresponden a unas dos propiedades básicas no-mercantiles del Mercado... ¡Correcto! - El cien por cien, es una tendencia o un plano (el tercer estado estacionario - martingala). En una martingala la integral de la FR debería dar cero en el infinito. Está claro. En una serie de precios reales, obtenemos MO>0 o MO<0, y podemos operar, aunque en este último caso tendremos que "invertir" el TS para que MO vuelva a ser mayor que cero (ver fig. derecha). La posición de la frontera cortada verticalmente viene determinada, como he mencionado antes, por el diferencial y el grado de previsibilidad del mercado. Cuanto más predecible sea el mercado, más cerca estará esta frontera de su límite H opt=2Sp. Cuanto más se parece el mercado a una martingala, más se desplaza este límite hacia la zona de valores más grandes de h y menos eficaz resulta la negociación.
Obsérvese que hasta ahora en la construcción de las ecuaciones de la OTC nunca hemos especificado tipos de regularidades que puede superar en los mercados, lo que nos trae beneficios. Las dependencias en BP, como sabemos, son lineales y todas las demás dependencias (no lineales). La identificación de las dependencias lineales en las series de precios no es una tarea fácil, pero es posible, mientras que las dependencias no lineales son más difíciles - su variedad es infinita y no hay un captador universal para ellas (si no es nuestro ОТС, por supuesto). Hay que identificar claramente cada una, ajustar un mecanismo específico para ella y rezar para que (la dependencia no lineal) no cambie inadvertidamente algún coeficiente de la serie de potencias que la describe). Por lo tanto, la presencia de no linealidades en BP causará no monotónicos (estoy hablando de TP sin órdenes de protección) en forma de oleadas suaves y adelgazamiento. En otras palabras, si las dependencias lineales modificarán la pendiente de la FR, las no lineales provocarán una deformación, por ejemplo, aparecerán colas gruesas, etc. Abajo a la izquierda se muestra un ejemplo de relación lineal entre muestras vecinas en el PDF:
El sistema de la derecha es muy poco lineal:-)
Por lo tanto, sólo tenemos un parámetro ajustable en TS - H opt y sólo un parámetro que caracteriza la condición del mercado - la inclinación de la pendiente de la FR. Este último parámetro, aparentemente, apenas depende de las características no lineales de los precios, por lo que la OET pretende ser integral (en el sentido de una manipulación completa de cualquier combinación de mercado).
P.D. Mierda, el post anterior se perdió...