Evaluación del riesgo en la secuencia de transacciones con un activo

Prefacio

Nos basaremos en la idea de Ralph Vince de la gestión del volumen de posiciones (en estas condiciones, será útil recordar la fórmula de Kelly). Se conoce como la «f óptima». En esta teoría, la f es una parte del capital que se arriesga en cada transacción. Según Vince, la f se selecciona dependiendo de las condiciones de la optimización (maximización) de los beneficios. Hay dos problemas que surgen cuando esta teoría se usa en el trading:

1. Una reducción (drawdown) muy grande de la cuenta.
2. La f se sabe sólo en el historial de las transacciones.

La solución de estos problemas es sólo uno de los objetivos de este artículo. Otro objetivo no menos importante es el intento ordinario de la introducción del cálculo de probabilidades y la estadística matemática en el proceso del análisis de los sistemas comerciales. Por eso vamos a apartarnos periódicamente del tema principal. Voy a abstenerme de la exposición sistemática de los fundamentos: en caso de necesidad, el usuario podrá dirigirse, por ejemplo, al libro "The Mathematics of Technical Analysis: Applying Statistics to Trading Stocks, Options and Futures".

Los ejemplos se muestran al final del artículo. Su objetivo consiste en ilustrar la teoría expuesta, por eso no se recomienda aplicarlos en el trading real.

Introducción. Falta de ambigüedad

Para que sea más fácil, supongamos que el precio del activo expresa el coste de su unidad en unidades del capital, y no al revés. El paso mínimo del volumen de la transacción es el valor fijo en unidades del activo. El volumen mínimo no nulo de la transacción es igual a este paso. Vamos a usar un modelo simple de la transacción.

Para cada transacción se define su tipo buy/sell, volumen v y los precios de entrada, Stop Loss y salida: penter, pstop y pexit, respectivamente.

Limitaciones evidentes:

• volumen no nulo v≥0
• el precio de salida tiene que ser menos que el precio de entrada para la compra: pstop<penter
  
• el precio de salida tiene que ser más que el precio de entrada para la venta: pstop>penter. 

Vamos a introducir las siguientes denominaciones:

• C0 — capital antes de entrar en la transacción;
• C1 — capital después de salir de la transacción;
• Cs — capital después de la activación precisa de Stop Loss;
• r — parte del capital inicial que se pierde cuando se activa el Stop Loss,

es decir, C0−Cs=rC0.

Para la transacción tipo buy: C1=C0+v(pexit−penter) и Cs=C0−v(penter−pstop).

Lo mismo para la transacción tipo sell: C1=C0+v(penter−pexit) и Cs=C0−v(pstop−penter).

Después de unas sencillas transformaciones, obtenemos C1=C0(1+ra), donde a=(pexit−penter)/(penter−pstop). Estas expresiones son ciertas para las transacciones de ambos tipos: buy y sell. Vamos a llamar el valor r el riesgo de la transacción, y el valor a, su rentabilidad.

Vamos a formular el problema de la gestión del riesgo para nuestro modelo. Que tengamos n transacciones con las rentabilidades ai, donde i=1..n, y es necesario estimar los riesgos ri. Hay que tomar en cuenta que ri pueden depender sólo de los valores conocidos para el momento de la entrada en la transacción. Habitualmente, se considera que todos los riesgos son iguales unos a otros ri=r, donde 0≤r<1, y encuentran r=rmax que maximiza el valor del beneficio Cn=C0(1+ra1)(1+ra2)…(1+ran).

Vamos a actuar de la manera parecida, pero con algunas diferencias: durante la maximización tendremos en cuenta algunas limitaciones. Por ejemplo, son limitaciones de la reducción máxima y la rentabilidad media en la serie de transacciones. Vamos a introducir las siguientes denominaciones:

• A0 es el menor de todos ai,
  
• A=(a1+a2+…+an)/n — su media aritmética.

Es cierto que siempre A0≤A y la igualdad se consigue sólo si todos ai=A0. Vamos a considerar las limitaciones en r más detalladamente.

1. Cn=Cn(r)>0, de donde se deduce que 1+rA0>0. Si A0≥−1, eso es cierto para todos 0≤r<1. En caso cuendo A0<−1, obtenemos que 0≤r<−1/A0. Vemos que la limitación adicional en r aparece sólo si hay transacciones, la salida de las cuales ha sido por Stop Loss con deslizamiento. Como resultado, la limitación tendrá el aspecto 0≤r<rc, donde rc=1 si A0≥−1, y rc=−1/A0 si A0<−1.

2. Vamos a definir la rentabilidad media g de la siguiente manera: Cn=C0(1+gr)^n, desde aquí:

   

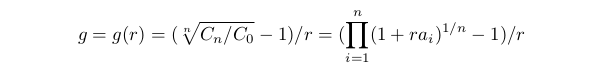
   En otras palabras, g puede ser llamado como beneficio medio de la transacción en la serie respecto al riesgo asumido. La función g(r) se define durante la ejecución de las limitaciones del punto anterior. Tiene una particularidad eliminable r=0: si r→0, entonces g(r)→A, y podemos aceptar que g(0)=A. Se puede mostrar que g(r)≡A, sólo si todos ai=A. En el mismo caso, si entre ai hay diferentes, entonces g(r) se disminuye cuando r crece. La limitación tendrá el aspecto g(r)≥G0>0. La constante G0 depende de muchos aspectos: condiciones del trading, preferencias del trader, etc. En el marco de este modelo, se puede decir que si G0>A, entonces el conjunto r que satisface a la desigualdad estará vacío. Si G0≤A, nuestra limitación tendrá el aspecto 0≤r≤rg, donde rg es la solución de la ecuación g(rg)=G0. Si esta ecuación no tiene solución, rg=1.

3. Para evaluar la reducción máxima vamos a considerar su valor opuesto:

   

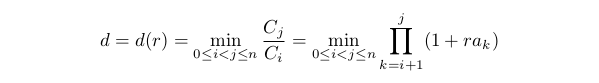
   Este valor puede ser llamado el crecimiento mínimo . Es más conveniente ya que es siempre positivo y finito, cuando se ejecuta la limitación especificada en el primer punto. Es evidente que d(0)=1. Si A0<0, entonces d(r) se disminuye cuando r crece en el área limitada por el primer punto. La limitación tendrá el siguiente aspecto: d(r)≥D0, donde 0<D0<1. Cuanto más grande sea D0, la menor reducción se permite. Vamos a reescribir nuestra limitación de la siguiente manera: 0≤r≤rd, donde rd es la solución de la ecuación d(rd)=D0 (si esta ecuación no tiene solución, rd=1).

4. Cuando entramos en la transacción, el volumen v no puede adquirir un valor aleatorio. Debe ser múltiple de algún valor Δv>0, o sea v=kΔv cuando k≥0 es entero. Luego, para la transacción i-sima:

   

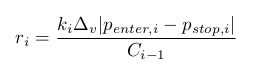
   Es evidente que la coincidencia de todos ri es poco probable. Por tanto, resulta que el problema de arriba no tiene una solución exacta. Por eso, vamos a buscar una solución aproximada. Por ahora nos limitaremos con el cálculo de un rv mínimo, para que cada ri pueda adquirir por lo menos un valor no nulo en el segmento [0,rv]

   

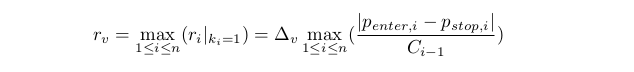
   Vamos a determinar también una evaluación más aproximada para rvr≥rv. De la ejecución de la limitación en el punto anterior se deduce que Ci≥D0C0>0. Obtenemos (nota: d0 y D0 significa lo mimso):

   

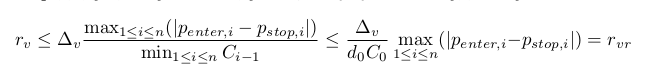
   Esta evaluación es más conveniente porque tiene una relación más simple con el capital. Depende sólo de su valor inicial.

Suponemos que el conjunto que satisface a tres primeras limitaciones no está vacío. Entonces, tiene el aspecto del segmento [0,ra], donde ra=min(rc,rg,rd).

Además, suponemos que también se ejecuta la cuarta limitación que requiere ra≥rv. Ahora, vamos a considerar el problema de la maximización Cn=Cn(r). En el caso significante para nosotros: A>0 y A0<0. Esta función crece en el segmento [0,rmax] y se disminuye en el segmento [rmax,rc]. Aquí, rmax es el punto de anulación de la primera derivada: dCn(r)/dr=0.

Ahora es más fácil encontrar ropt, que maximiza Cn(r) en el segmento [0,ra]: ropt=min(ra,rmax). Quedan dos casos: 1) A0≤A≤0 и 2) 0≤A0≤A. En el primer caso, ropt=rmax=0, y en el segundo caso,  rmax=rс и ropt=ra .

A continuación, vamos a considerar el caso cuando el conjunto definido por las limitaciones está vacío. Es posible sólo en dos ocasiones: 1) G0>A o 2) ra<rv. Aquí, sólo nos queda aceptar que ropt=0.

Ahora, encontraremos los valores aproximados ri tomando en cuenta la discreción de los volúmenes de las transacciones. Que Ri sea un conjunto finito no vacío de los números en el segmento [0,ra] apropiados para el valor del riesgo ri en la transacción i. Seleccionamos de ellos ropt,i que maximiza Cn(r) en Ri. Si ropt∈Ri, entonces ropt,i=ropt. Si ropt∉Ri, entonces son posibles dos situaciones: 1) todos los puntos Ri se encuentran por un lado de ropt y 2) los puntos Ri se encuentran por ambos lados de ropt. En el primer caso, como ropt,i cogemos de Ri el punto más próximo a ropt. En el segundo caso, cogemos de Ri dos puntos más próximos a ropt de ambos lados. Y como ropt,i, seleccionamos aquél punto cuyo valor Cn(r) es mayor.

Incertidumbre. Ejemplo introductorio

Vamos a hacer que el modelo estudiado en la introducción sea más complicado. Vamos a suponer que sabemos n números de ai, pero desconocemos su orden. Por tanto, se permite su transposición aleatoria. Veremos qué se cambiará en los resultados obtenidos antes. En dos primeros puntos, la transposición aleatoria de ai no cambiará nada. En el cuarto punto, tampoco habrá cambios si usamos la evaluación más aproximada de rvr.

Los cambios son posibles en el tercer punto. Efectivamente, se puede componer la secuencia de tal manera que entre los números negativos no habrá positivos, y entonces la reducción será máxima. Y al revés, se puede mesclar regularmente los números positivos con los negativos, y eso disminuirá la reducción. El número total de transposiciones en caso general será igual a n!. Es una cantidad muy grande ya con n estando en el rango de varias decenas. Teóricamente, podemos resolver el problema planteado en la introducción para cada una de j=1..n! transposiciones de la secuencia ai y obtener un conjunto de los números rd,j. Pero incluso en este caso se mantiene la pregunta, ¿qué transposición hay que elegir exactamente? Para trabajar con semejante incertidumbre de una manera enjundiosa, necesitamos los conceptos y los métodos de la teoría de la probabilidad y la estadística matemática.

Vamos a considerar un conjunto de números rd,j como los valores de la función ρd=ρd(j)=rd,j que depende de la transposición. Es decir, hablando en términos de la teoría de la probabilidad, ρd es un valor aleatorio, cuyo conjunto de los eventos elementales será el conjunto de transposiciones n. Vamos a considerarlas todas como diferentes, incluso si algunas ai coinciden.

Además, vamos a considerar todas las transposiciones nde igual probabilidad. Entonces, la probabilidad de cada una de ellas será igual a 1/n!, lo cual establece una medida probabilista en un conjunto de eventos elementales. Ahora podemos definir la distribución de probabilidades Pρd(x)=n(x)/n! para ρd, donde n(x) es el número de transposiciones n para las cuales rd,j<x. Ahora tenemos que especificar la condición de la limitación de la reducción. Aparte del mínimo permitido D0 , tenemos que indicar el nivel aceptable de la importancia 0<δ<<1. El valor δ muestra la probabilidad de la superación de la reducción por encima del límite que consideramos despreciable. Entonces, podemos definir rd(δ) como el cuantil δ de la distribución Pρd(x). Para encontrar una solución aproximada de este problema, vamos a generar aleatoriamente una cantidad bastante grande de nt, donde 1<<nt<<n!, transposiciones n. Encontraremos el valor rd,j para cada una de ellas, donde 1≤j≤nt. Luego, como evaluación para rd(δ), podemos coger un cuantil aleatorio δ de la población de estas rd,j.

A pesar de un cierto artificio de este modelo, se puede encontarle su aplicación. Por ejemplo, se puede coger rd calculado para una serie inicial de transacciones y definir el valor de la probabilidad pd=Pρd(rd). Obviamente, la desigualdad 0≤pd≤1 es válida. pd próximo a cero significa una reducción grande debido a la reunión de las transacciones no rentables cercanas unas a las otras; y próximo a uno indica en una mezcla uniforme de las ganancias y las pérdidas. De esta manera, no sólo descubrimos la presencia de las series de las pérdidas en una secuencia de transacciones (como por ejemplo en el método del cálculo Z), sino también el grado de su influencia en la reducción. Se puede generar otros índices, que dependen sólo de Pρd(), o también de rd.

Incertidumbre. Caso general

Supongamos que tenemos una secuencia de transacciones con beneficios ai, 1≤i≤n. También vamos a suponer que esta secuencia es una implementación concreta de la secuencia de unos valores aleatorios λi, independientes en su población y distribuidos idénticamente. Vamos a definir su función de la distribución de las probabilidades como Pλ(x). Se supone que tiene las siguientes propiedades: 

• esperanza condicional positiva Mλ
  
• limitación por debajo. Hay un número λmin≤−1, para el que Pλ(x)=0 cuando x<λmin y Pλ(x)>0 cuando x>λ0.
  

Estas condiciones significan que en promedio el rendimiento es positivo. Y aunque las transacciones con pérdidas son posibles, siempre existe la posibilidad de no perder todo el capital en una sola transacción, limitando el riesgo.

Vamos a formular nuestro problema de identificación de la magnitud del riesgo. Igual como en el ejemplo de la parte anterior del artículo, tenemos que estudiar el valor aleatorio ρopt, en vez del número ropt calculado en la inroducción. Luego, teniendo establecido el nivel de la importancia δ, calcularemos ropt=ropt(δ), como cuantil δ de la distribución Pρopt(x). En el futuro, podemos usar nuestro sistema con este riesgo, hasta que la reducción y el beneficio medio se encuentren dentro de los límites establecidos. Al salir fuera de estos límites, tenemos que rechazar este sistema. La probabilidad del error no no va a exceder δ.

Me gustaría llamar atención en la importancia de que δ tenga un valor pequeño. Si δ es grande, se pierde el sentido de usar el criterio obtenido. Sólo en el caso de un valor pequeño, dos eventos pueden considerarse como vinculados uno con otro: 1) el sistema no funciona debido al cambio del mercado y 2) ha tenido lugar una reducción demasiado grande o una rentabilidad demasiado pequeña. Aparte del error que ya ha sido discutido, se puede considerar el error de otro tipo. Cuando ocurre este error, no notamos los cambios del mercado que no influyen en la reducción y rentabilidad de nuestro sistema. Desde el punto de vista práctico, claro que no hay sentido considerar este error, ya que no afecta la rentabilidad del sistema.

En nuestra teoría, eso se refleja en que los cambios de las distribuciones Pλ(x) y Pρopt(x) no nos importan. Sólo nos importa el cambio del cuantil δ de Pρopt(x). Particularmente, eso significa la ausencia del requerimiento de la estacionaridad para la secuencia de los beneficios. Aunque la necesitamos de cualquier forma para recuperar la ley de distribuciones de rentabilidades en el muestreo final ai, 1≤i≤n. Aquí, el requerimiento de una distribución que no se cambia significativamente puede ser suficiente, en vez de una estacionaridad absoluta.

Al fin y al cabo, ρopt se expresa a través de λi, aunque de una manera bastante complicada (a través de otras variables aleatorias intermedias). Por eso tendremos que estudiar las variables aleatorias, definidas como funciones de λi, y construir sus distribuciones. Para eso, en su lugar, necesitamos saber Pλ(x). Vamos a nombrar tres variantes de la información sobre esta distribución que tenemos que poseer.

1. Se sabe una expresión exacta para Pλ(x), o hay una manera de construir una aproximación aleatoriamente exacta para el sistema comercial que se analiza. Generalmente, eso es posible sólo cuando haya unas suposiciones bastante fundamentadas sobre el comportamiento de una serie de los precios del activo. Por ejemplo, podemos considerar la teoría del «paseo aleatorio» como cierta. Pero normalmente, el uso de esta información directamente en el trading es poco probable. Las conclusiones sacadas de esta manera siempre son poco realistas, y a menudo deniegan la posibilidad de obtener los beneficios en principio. Aquí, la ventaja consiste en otra cosa. A base de estas suposiciones, se construye la hipótesis nula, como se dice en la estadística matemática. Luego, usando los datos empíricos y las pruebas de concordancia, podemos descartar esta hipótesis, o bien aceptar que es imposible descartarla con nuestros datos. En nuestro caso, esta información empírica es la secuencia ai, 1≤i≤n.
2. Se sabe que Pλ(x) pertenece o se aproxima bien a una familia paramétrica de distribuciones. Por ejemplo, es posible cuando las suposiciones sobre los precios de un activo del punto anterior no se infringen mucho. Desde luego, el tipo de la familia de distribuciones se define también por el algoritmo del sistema comercial. Los valores exactos para los parámetros de la distribución se calculan usando la secuencia ai, 1≤i≤n por los métodos de la estadística paramétrica.
3. Aparte de la secuencia ai, 1≤i≤n, se saben (o se suponen) sólo algunas propiedades comunes de Pλ(x). Por ejemplo, puede ser la suposición sobre la existencia de la esperanza condicional y dispersión finitas. En este caso, vamos a usar la función de distribución empírica como aproximación para Pλ(x). Vamos a construirla basándose en la misma secuencia ai, 1≤i≤n. Los métodos que utilizan la función de distribución empírica en vez de la exacta suelen llamarse el bootstrap. En algunos casos, no es necesario saber Pλ(x). Por ejemplo, la variable aleatoria (λ1+λ2+…+λn)/n cuando n son grandes, puede considerarse como normalmente distribuida (con la dispersión finita λi).
   

Este artículo va a continuar con el uso de las suposiciones descritas en la tercera variante. Las dos primeras variantes serán descritas en el futuro.

Estudiaremos cómo se cambiarán los cálculos realizados en la introducción. En vez de los números absolutos A0 y A, vamos a trabajar con las variables aleatorias que se expresan a través de λi de la misma manera: Λ0=min(λ1, λ2, …, λn) и Λ=(λ1+λ2+…+λn)/n.

Vamos a considerar su comportamiento asintótico cuando n crece sin restricciones. En este caso, es siempre y con una buena velocidad Λ0→λmin. Supongamos que λi  tiene una dispersión finita Dλ, entonces Λ→Mλ. Además, como ya hemos mencionado antes, se puede considerar con buen grado de precisión que Λ es normalmente distribuida con la esperanza condicional Mλ y la dispersión Dλ/n. Si los valores exactos de Mλ y Dλ se desconocen, se puede usar sus análogos de muestreo calculados por ai. Además, se puede construir las distribuciones empíricas para Λ0 y Λ, usando el bootstrap.

Antes de calcular ropt(δ) con el método de bootstrap, tomaremos en cuenta las siguientes observaciones sobre cómo se cambiarán los cálculos realizados en la intoducción:

1. En el primer punto, debido al comportamiento asintótico de Λ0, se puede simplemente ajustar la evaluación hasta el valor rc=−1/λmin. Pero para la distribución empírica, el valor λmin coincide con А0 y, por tanto, todo queda sin cambios en este punto.
   
2. Es necesario asegurarse de que la condición G0≤Λ se altera con la condición no más de δ. Para eso, el cuantil δde Λ debe ser no menos de G0. Para un cálculo aproximado de este cuantil, usaremos la aproximación normal de la distribución Λ. Como resultado, obtendremos nmin —la estimación de abajo del número de transacciones necesario para el análisis. Además, se puede ajustar un poco el método estándar del bootstrap, y construir los conjuntos de los muestreos de la longitud creciente para buscar nmin. Pero desde el punto de vista de la teoría, obtendremos más o menos lo mismo que para la aproximación con la distribución normal.
   
3. En el cuarto punto, como antes, usamos la evaluación más aproximada de rvr
   .

Establecemos nb —el número de las secuencias de los beneficios que va a generarse. En el ciclo de la ejecución del botstrap, tenemos que recorrer las limitaciones descritas en la introducción por la magnitud del riesgo para cada j=1..nb. Considerando lo mencionado arriba, sólo nos queda calcular rg(j), rd(j), rmax(j) y ropt(j). Si el conjunto para r con el que j está vacío, suponemos que ropt(j)=0.

Cuando el bootstrap termine su trabajo, tendremos un array de valores ropt[]. Después de calcular el cuantil de muestreo δ usando este array, vamos a cogerlo como solución del problema planteado.

En vez de la conclusión

Se puede decir que lo expuesto más arriba es sólo el comienzo del tema. Voy a mencionar brevemente a qué estarán dedicados los siguientes artículos.

• Para usar el modelo de las transacciones como secuencia de las distribuciones igualmente independientes, tenemos que hacer algunas suposiciones e hipótesis sobre los precios del activo y algoritmo comercial.
• Hay que concretizar la teoría para algunos modos particulares de la salida de las transacciones: 1) los stop-loss/take-profit fijos, 2) trailing stop fijo.
• Es necesario demostrar cómo se puede usar la teoría expuesta para construir los sistemas comerciales. Veremos cómo se puede usar la teoría de probabilidades para la construcción del sistema en las brechas (gaps). Tocaremos brevemente el tema del uso del aprendizaje automático.
  

Anexo a la introducción

A continuación, se muestra el texto del script r_intro.mq5 y los resultados de su trabajo, en forma de los gráficos y números.

#include <Graphics\Graphic.mqh>
#define N 30
#define NR 100
#property script_show_inputs
input int ngr=0;    // número del gráfico a mostrar en la pantalla
double G0=0.25;     // rentabilidad media mínima
double D0=0.9;      // crecimiento mínimo más pequeño
                    // se supone que el capital inicial c0 es igual a 1


void OnStart()
  {
   double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // rentabilidad de transacciones
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N;
   rc=1; if(A0<-1) rc=-1/A0;
   double c[N];
   r[0]=0; cn[0]=1; g[0]=A; d[0]=1;
   for(int i=1; i<NR;++i)
     {
      r[i]=i*rc/NR;
      cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j];
      g[i]=(MathPow(cn[i],1.0/N)-1)/r[i];
      c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c);
     }
   int nrg,nrd,nra,nrmax,nropt;
   double b[NR];
   for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0);
   nrg=ArrayMinimum(b); rg=r[nrg];
   for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
   nrd=ArrayMinimum(b); rd=r[nrd];
   nra=MathMin(nrg,nrd); ra=r[nra];
   nrmax=ArrayMaximum(cn); rmax=r[nrmax];
   nropt=MathMin(nra,nrmax); ropt=r[nropt];
   Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt,
         "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt],
         "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt],
         "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]);
   if(ngr<1 || ngr>5) return;
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   graphic.Create(0,"G",0,0,0,750,350);
   double x[2],y[2];
   switch(ngr)
     {
      case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0;
      graphic.CurveAdd(x,y,CURVE_LINES,"g=G0");
      x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rg");
      break;
      case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)");
      x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0;
      graphic.CurveAdd(x,y,CURVE_LINES,"d=D0");
      x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rd");
      break;
      case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)");
      x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)");
      x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax");
      x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)");
      x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt];
      graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt");
      break;
      case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt");
      break;
      case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]);
      graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax");
      break;
     }
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(30000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
  }

// la función dcalc() recibe el array de valores c1, c2, ... cN y
// devuelve el crecimiento mínimo d. Suponemos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }

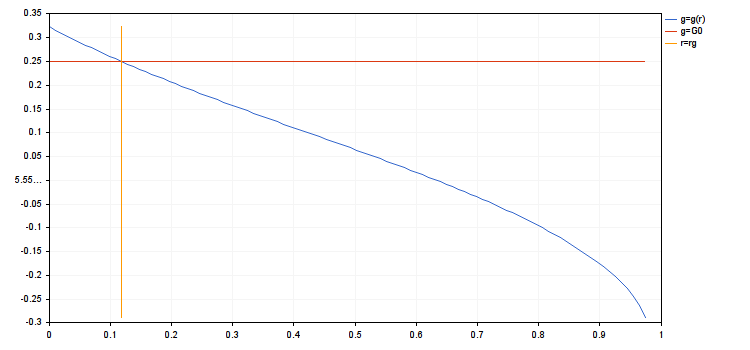
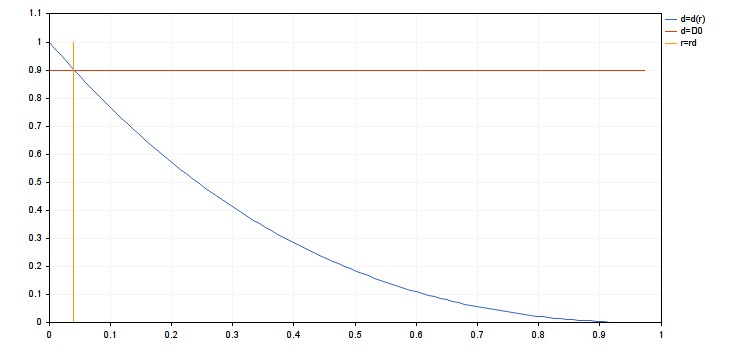
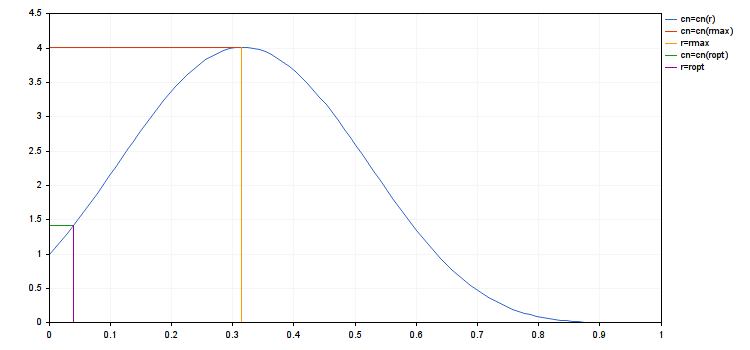
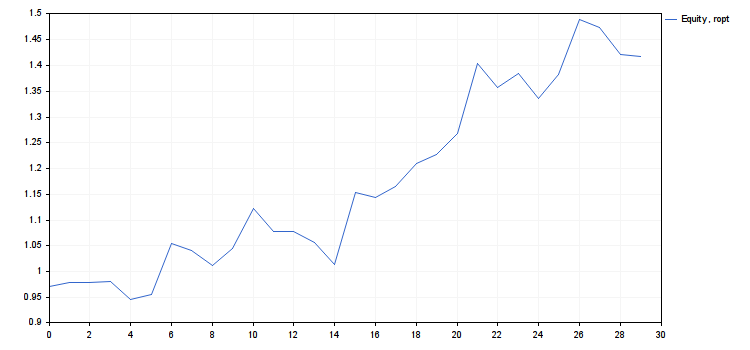
• rc = 0.9839614287119945
• rg = 0.1180753714454393
• rd = 0.03935845714847978
• ra = 0.03935845714847978
• rmax = 0.3148676571878383
• ropt = 0.03935845714847978
• g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
• d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
• cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712

Como podemos ver, si usamos rmax como el valor para el riesgo, obtenemos un beneficio mucho más grande (300% en vez de 40%). Pero eso se consigue debido una reducción mucho más grande (más de 60% en vez de 10%). Además, hay que tomar en cuenta una diferencia casi doble para la rentabilidad media. Si es más pequeña, el incremento de los gastos transaccionales llevará a la caída más grande de beneficios. Por estas razones, surgen las siguientes conclusiones:

1. Usar ropt como valor para el riesgo en este sistema.
2. El riesgo «liberado» rmax−ropt puede ser usado para añadir nuevos sistemas (diversificación).
   

Anexo al ejemplo introductorio

A continuación, se muestra el texto del script r_exmp.mq5 y los resultados numéricos de su trabajo.

#include <Math\Stat\Uniform.mqh>
#define N 30      // longitud de la serie de transacciones
#define NR 500    // número de los intervalos de la división del segmento [0,rc]
#define NT 500    // número de las transposiciones generadas
double D0=0.9;    // crecimiento mínimo más pequeño
double dlt=0.05;  // nivel de importancia

void OnStart()
  {
   double A0,rc,r[NR],d[NR],rd[NT],a[N]=//A,rg,ra,rmax,ropt,g[NR],cn[NR],
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// rentabilidad de transaciones
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   A0=a[ArrayMinimum(a)];
   rc=1; if(A0<-1) rc=-1/A0;
   for(int i=0; i<NR;++i) r[i]=i*rc/NR;
   double b[NR],c[N];
   int nrd;
   MathSrand(GetTickCount());
   for(int j=0; j<NT;++j)
     {
      trps(a,N);
      for(int i=1; i<NR;++i)
        {
         c[0]=1+r[i]*a[0];
         for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]);
         d[i]=dcalc(c);
        }
      for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0);
      nrd=ArrayMinimum(b); rd[j]=r[nrd];
     }
   double p[1],q[1]; p[0]=dlt;
   if(!MathQuantile(rd,p,q)) {Print("MathQuantile() error"); return;}
   PrintFormat("el cuantil de muestra %f de rd[] es igual a %f",p[0],q[0]);
   double rd0=0.03935845714847978;   // valor de rd obtenido en la Introducción
   double pd0=0;                     // el valor pd que le corresponde
   for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT;
   PrintFormat(" para rd = %f el valor pd = %f",rd0,pd0);
  }
// la función dcalc() recibe el array de valores c1, c2, ... cN y
// devuelve el crecimiento mínimo d. Suponemos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(int i=1; i<N;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
// transposición aleatoria de las primeras no más de min(n,ArraySize(b))
// elementos del array b[]
// en vez de trps() se puede usar MathSample() de la librería
void trps(double &b[],int n)
  {
   if(n<=1) return;
   int sz=ArraySize(b);
   if(sz<=1) return;
   if(sz<n) n=sz;
   int ner;
   double dnc=MathRandomUniform(0,n,ner);
   if(!MathIsValidNumber(dnc)) {Print("Error ",ner); ExpertRemove();}
   int nc=(int)dnc;
   if(nc>=0 && nc<n-1)
     { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;}
   trps(b,n-1);
  }

• el cuantil de muestreo 0,05 rd[] es igual a 0,021647
• para rd = 0,039358 el valor pd = 0.584

La primera línea de los resultados nos dice que tenemos que disminuir el riesgo casi dos veces, en comparación con el resultado obtenido en la Introducción. En este caso, si la reducción supera la reducción del objetivo (10%), en el futuro eso va a significar que probablemente el sistema no funcione como es debido, y habrá que dejar de tradear con él. La probabilidad del error (el sistema de trabajo es rechazado) en este caso será de δ (0,05 o 5%). La segunda línea del resultado nos dice que la reducción en la serie inicial de transacciones es un poco más pequeña que podría ser en promedio. Es muy probable que 30 transacciones no sean suficientes para evaluar este sistema. Por eso sería útil realizar semejante análisis para una cantidad mayor de transacciones y ver cómo se cambian los resultados.

Anexo al caso general

Abajo se muestra el script r_cmn.mq5, en el que intentaremos evaluar de abajo el valor nmin y los resultados de su trabajo:

#include <Math\Stat\Normal.mqh>
#include <Math\Stat\Uniform.mqh>
#include <Graphics\Graphic.mqh>
#define N 30        // longitud de la serie de transacciones
#define NB 10000    // número de los muestreos generados para el bootstrap
double G0=0.25;     // rentabilidad media mínima
double dlt=0.05;   // nivel de importancia

void OnStart()
  {
   double a[N]=
     {
      -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,   // rentabilidad de transacciones
      2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745,
      -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850,
      0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375,
      -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775
     };
   double A=MathMean(a);
   double S2=MathVariance(a);
   double Sk=MathSkewness(a);
   double Md=MathMedian(a);
   Print("parámetros de muestreo de la distribución:");
   PrintFormat("media: %f, dispersión: %f, asimetría: %f, mediana: %f",A,S2,Sk,Md);
   PrintFormat("número de transacciones: %d, valor dlt: %f, valor G0: %f",N,dlt,G0);
// aproximación por la distribución normal
   Print("aproximación por la distribución normal:");
   double q0, p0;
   int ner;
   q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
   Print("cuantil dlt: ",q0);
   p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   Print("nivel de importancia para G0: ",p0);
// bootstrap
   MathSrand(GetTickCount());
   double b[N],s[NB];
   p0=0;
   for(int i=0;i<NB;++i)
     {
      sample(a,b);
      s[i]=MathMean(b);
      if(s[i]<G0) ++p0;
     }
   p0/=NB;
   double p[1],q[1];
   p[0]=dlt;
   if(!MathQuantile(s,p,q)) {Print("MathQuantile() error"); return;}
   Print("aproximación por bootstrap");
   Print("cuantil dlt: ",q[0]);
   Print("nivel de importancia para G0: ",p0);
// definición de nmin (aproximación por la distribución normal)
   int nmin;
   for(nmin=1; nmin<1000;++nmin)
     {
      q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner);
      if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;}
      if(q0>G0) break;
     }
   Print("Número mínimo de transacciones nmin (aproximación por la distribución normal):");
   PrintFormat("no menos de %d, valor del cuantil dlt: %f",nmin,q0);
  }
  
void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   for(int i=0; i<N;++i)
     {
      dnc=MathRandomUniform(0,N,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==N) nc=N-1;
      b[i]=a[nc];
     }
  }

Parámetros de muestreo de la distribución:

• media: 0,322655
• dispersión: 1,419552
• asimetría: 0,990362
• mediana: 0,023030
• número de transacciones: 30
• valor dtl: 0,050000
• valor G0: 0.250000.
  

Aproximación por la distribución normal:

• cuantil dlt: -0,03514631247305994;
• nivel de importancia para G0: 0,3691880511783918.
  

Aproximación por bootstrap:

• cuantil dlt: -0,0136361;
• nivel de importancia para G0: 0,3727.
• número mínimo de transacciones nmin (aproximación por la distribución normal): no menos de 728
• valor del cuantil dlt: 0,250022.
  

De estos resultados, se deduce inmediatamente que ropt(δ)=0. Eso quiere decir que nuestro criterio prohíbe tradear usando este sistema con estos datos, o requiere el historial de transacciones de una longitud más grande. Y eso, a pesar de unos magníficos gráficos del capital en el primer anexo. Y eso que el bootstrap produce prácticamente los mismos resultados que la aproximación por la distribución normal. Es natural que surgen preguntas: 1) ¿por qué todo sale tan mal? y 2) ¿cómo mejorarlo? Intentaremos contestar a esas preguntas.

1. La razón consiste tanto en el criterio utilizado, como en el propio sistema. Nuestro criterio es demasiado universal. Por un lado, eso está bien: es fácil utilizarlo en la mayoría de los casos. Por otro lado, él no considera las particularidades no sólo del sistema en cuestión, mucho menos las particularidades de todos los sistemas analizados por nosotros. Por ejemplo, todos nuestros sistemas producen las distribuciones con el lado izquierdo «cortado», y algunos pueden tener teóricamente una esperanza condicional infinita. Por eso, normalmente, todas las distribuciones están abiseladas a la derecha, y su media se converge demasiado lento a la distribución simétrica normal. El sistema de nuestro ejemplo tiene precisamente esta distribución biselada, a juzgar por el coeficiente de la asimetría o por el desplazamiento de la esperanza condicional a la derecha de la mediana. En principio, precisamente este comportamiento ha de esperar del sistema que sigue la regla «recorta las pérdidas, permite que crezcan los beneficios».
2. Necesitamos los criterios que utilizan la información más completa sobre un cierto sistema de trading y sobre la serie de los precios del activo. Es decir, no se puede descartar por completo las suposiciones sobre los precios. Pero estas suposiciones no deben distorsionar demasiado la situación real. Eso quiere decir que tenemos que encontrarnos en la situación de la segunda variante de tres puntos, al principio del apartado «Caso general». Precisamente por eso tenemos que ocuparnos de los métodos paramétricos. Desde el punto de vista computacional, son más complicados y menos universales, pero pueden ser más precisos en cada caso particular.

Se puede hacer la siguiente conclusión. Las pérdidas no se deben solamente a los cambios inesperados en el comportamiento de los precios del activo (por ejemplo, el cambio de la tendencia). También pueden ser causadas por la incertidumbre propia a ellos (volatilidad, ruido). Los métodos considerados por nosotros es una de las maneras de intentar separar esta razones y reducir la influencia de la segunda. Si no se consigue realizar eso para un sistema comercial, no se recomienda utilizarlo.