Developing a Replay System — Market simulation (Part 24): FOREX (V)

Introduction

In the previous article "Developing a Replay System — Market simulation (Part 23): FOREX (IV)", we looked at the implementation of partial blocking of the simulation system. The block was necessary because the system encountered difficulties in dealing with extremely low transaction volumes. This limitation became apparent when attempting to run simulations based on the Last plotting type, where the system was at risk of crashing when attempting to generate the simulation. This problem was especially noticeable in those moments when the volume of trades represented by the 1-minute bar was insufficient. To solve this issue, today we'll look at how to adapt the implementation and follow the principles that were previously used in simulation based on Bid plotting. This approach is widely used in the forex market, so this is already the fifth article on this topic. But in this case, we will not pay attention specifically to currencies as our goal is to improve the stock market simulation system.

Let's start implementing the changes

The first step is to introduce a private structure into our class. This is because we have data that is common to both Last and Bid simulation modes. These common elements, which are essentially values, will be combined into a single structure. So we define the following structure:

struct st00
{
   bool    bHigh, bLow;
   int     iMax;
}m_Marks;

Although this looks like is a simple structure, it is robust enough to allow us to improve our code. By gathering all common values in one place we greatly increase the efficiency of our work.

After this preparation, we can begin the first real modification of the code.

inline int Simulation(const MqlRates &rate, MqlTick &tick[])
   {
      m_Marks.iMax = (int) rate.tick_volume - 1;
      m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high);
      m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low);
      Simulation_Time(rate, tick);
      if (m_IsPriceBID) Simulation_BID(rate, tick);
      else Simulation_LAST(rate, tick);
      else return -1;
      CorretTime(tick);

      return m_Marks.iMax;
   }

Today we will remove a limitation that has been preventing simulations based on the Last price and will introduce a new entry point specifically for this type of simulation. The entire operating mechanism will be based on the principles of the forex market. The main difference in this procedure is the separation of Bid and Last simulations. However, it is important to note that the methodology used to randomize the time and adjust it to be compatible with the C_Replay class remains identical in both simulations. This consistency is good because if we change one of the modes, the other one will also benefit, especially when it comes to managing time between ticks. Naturally, the modifications discussed here will also affect simulation based on the Bid plotting type. These changes are fairly easy to understand, so I won't go into the details.

Let's go back to our target code. Once we add a call to the Last-based simulation function, we can see the first point of this call. Below is the internal structure of this function:

inline void Simulation_LAST(const MqlRates &rate, MqlTick &tick[])
   {
      if (CheckViability_LAST(rate))
      {
      }else
      {
      }
      DistributeVolumeReal(rate, tick);
   }

In this context, we will perform two important steps when working with Last plotting. The first step is to test the possibility of using a random walk system for simulation, as discussed in previous articles. For those who have not studied this topic, I recommend reading the article "Developing a Replay System — Market simulation (Part 15): Birth of the SIMULATOR (V) - RANDOM WALK". The second step is to distribute trading volume between possible ticks. These steps are important when working with simulation based on the Last plotting type.

Before describing the structure in detail, let's look at two critical functions for Last-based simulatoin. The first function is shown below:

inline bool CheckViability_LAST(const MqlRates &rate)
   {
#define macro_AdjustSafetyFator(A) (A + (A * 1.4));
                                
      double  v0, v1, v2;
                                
      v0 = macro_AdjustSafetyFator(rate.high - rate.low);
      v1 = (rate.open - rate.low);
      v2 = (rate.high - rate.open);
      v0 += macro_AdjustSafetyFator(v1 > v2 ? v1 : v2);
      v1 = (rate.close - rate.low);
      v2 = (rate.high - rate.close);
      v0 += macro_AdjustSafetyFator(v1 > v2 ? v1 : v2);
      return ((int)(v0 / m_TickSize) < rate.tick_volume);
                                
#undef macro_AdjustSafetyFator
   }

This function is responsible for checking the possibility of generating a random walk within the available limits. How is it done? The method determines the number of ticks currently available for use. This information is provided by the bar we'll be working with, along with the number of ticks we need to cover, which is then calculated within the function.

Note that we will not directly use this value to determine the area to cover. This is because if we used such a direct approach, the resulting random walk would look artificial, with overly predictable movements. To mitigate this problem, we will adjust the calculations. This setting, implemented using a macro, defines a 30% larger region that acts as a safety factor for the correct generation of the random walk. Another important aspect is the need to always take into account the largest possible distance in the calculations, since randomization may require such an extension. Thus, this possibility has already been taken into account in the calculation process.

The end result indicates whether it is appropriate to use a random walk method or whether another, more direct randomization method should be used. However, this decision is made by the calling procedure, not here.

Below we describe the second function in detail:

inline void DistributeVolumeReal(const MqlRates &rate, MqlTick &tick[])
   {
      for (int c0 = 0; c0 <= m_Marks.iMax; c0++)
         tick[c0].volume_real = 1.0;
      for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--)
         tick[RandomLimit(0, m_Marks.iMax)].volume_real += 1.0;                                  
   }

Here the goal is to randomly distribute the total volume of trades on a 1-minute bar. The first loop performs the main distribution to ensure that each tick receives a minimum initial volume. The second loop is responsible for randomly distributing the remaining volume to prevent it from being concentrated in one tick. Although this possibility still exists, it is greatly reduced by the distribution methodology adopted.

These functions were already part of the original implementation and were discussed in the articles on the random walk implementation. However, this time we are taking a more modular approach to maximize the reusability of the developed code.

After further reflection, we identified elements that still remain common to the Bid and last simulations. These include the definition of entry and exit points, as well as the ability to define end points. Given this point, we strive to reuse previously developed codes. To do this, we need to change the code that was presented in the previous article. The change is as follows:

inline void Mount_BID(const int iPos, const double price, const int spread, MqlTick &tick[])
inline void MountPrice(const int iPos, const double price, const int spread, MqlTick &tick[])
   {
      if (m_IsPriceBID)
      {
         tick[iPos].bid = price;
         tick[iPos].ask = NormalizeDouble(price + (m_TickSize * spread), m_NDigits);
      }else
         tick[iPos].last = NormalizeDouble(price, m_NDigits);
   }

We start by replacing the old function name with the new one, and then insert an internal test to determine whether the simulation will be based on Bid or Last plotting type. Thus, the same function can be adapted to generate ticks based on Bid and Last values according to the data observed in the 1-minute bar file.

This change also requires two adjustments. Our goal is to integrate Bid and Last simulation in a simplified manner so that only the truly unique aspects of each are handled by the appropriate method. Other points will be handled on a general basis. Below are changes in the simulation class code:

inline void Simulation_BID(const MqlRates &rate, MqlTick &tick[])
   {
      Mount_BID(0, rate.open, rate.spread, tick);     
      for (int c0 = 1; c0 < m_Marks.iMax; c0++)
      {
         Mount_BID(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick);
         MountPrice(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick);
         m_Marks.bHigh = (rate.high == tick[c0].bid) || m_Marks.bHigh;
         m_Marks.bLow = (rate.low == tick[c0].bid) || m_Marks.bLow;
      }
      if (!m_Marks.bLow) Mount_BID(Unique(rate.high, tick), rate.low, rate.spread, tick);
      if (!m_Marks.bHigh) Mount_BID(Unique(rate.low, tick), rate.high, rate.spread, tick);
      Mount_BID(m_Marks.iMax, rate.close, rate.spread, tick);
   }

The crossed-out lines are removed to ensure the code continues to function correctly. However, to display Last, we need these crossed-out parts in a form that is common for the entire simulation system. So this common code was transfered into the function below:

inline int Simulation(const MqlRates &rate, MqlTick &tick[])
   {
      m_Marks.iMax = (int) rate.tick_volume - 1;
      m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high);
      m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low);
      Simulation_Time(rate, tick);
      MountPrice(0, rate.open, rate.spread, tick);    
      if (m_IsPriceBID) Simulation_BID(rate, tick);
      else Simulation_LAST(rate, tick);
      if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick);
      if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick);
      MountPrice(m_Marks.iMax, rate.close, rate.spread, tick);
      CorretTime(tick);

      return m_Marks.iMax;
   }

And now we have come to the decisive moment. Without significant changes, only through intelligent code reuse, we were able to integrate both simulations. Thus, we now have a simulation based on the Bid and Last plotting types. We automatically include input, output, and limit values if they were not previously specified in the randomized simulation. With this strategic adjustment, we have significantly expanded the scope of our simulation system. In addition, the complexity of the code has not increased and the code itself has not grown much. If you use the code that has been presented so far, you will get good performance for Bid-based simulation. And you will be able to play at least one bar on the chart with the Last plotting type. Well, the minimum value will be wrong as it will be zero, even though it is defined with the correct value. This is because for uninitialized ticks with only the time defined, all Last values are equal to zero. This would not be a problem if it were not for the fact that we have already distributed the volume traded. So, let's go back to our function that puts Last price values in each tick. We need to provide simulation with correct data.

Our Last price simulation function remains unchanged. However, when looking at the Bid simulation code, a thought arises: Couldn't we use the same code to simulate the Last price, especially if the number of available ticks is not enough to fully perform a random walk? I also had this question. After careful analysis, we concluded that only minor modifications to the Bid modeling function were needed. However, to avoid confusion in the future when we have to make changes to the code, we will need to carefully plan for these changes now. The Bid simulation procedure is launched by the function just mentioned. Given that the Last simulation concept is similar, we can look for a way to keep the previous call intact. Thus, we adapt the Bid simulation function so that it can also cover Last simulation in situations where a random walk is not applied.

Some may question this approach, but here's how the simulation code for Bid plotting was adapted to include simulation for Last-based plotting.

inline void Simulation_BID(const MqlRates &rate, MqlTick &tick[])
inline void Random_Price(const MqlRates &rate, MqlTick &tick[])
   {
      for (int c0 = 1; c0 < m_Marks.iMax; c0++)
      {
         MountPrice(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick);
         m_Marks.bHigh = (rate.high == (m_IsPriceBID ? tick[c0].bid : tick[c0].last)) || m_Marks.bHigh;
         m_Marks.bLow = (rate.low == (m_IsPriceBID ? tick[c0].bid : tick[c0].last)) || m_Marks.bLow;
         m_Marks.bHigh = (rate.high == tick[c0].bid) || m_Marks.bHigh;
         m_Marks.bLow = (rate.low == tick[c0].bid) || m_Marks.bLow;
      }
   }

To avoid runtime confusion, I decided to rename the function. It's a small price to pay for the benefit of getting more universal code. The idea of this adaptation is as follows. These two code elements deserve special attention. The ternary operator, although considered obscure by some, is a valuable legacy of the C language that offers a lot of useful things. These segments check the type of plotting to adjust the price accordingly. Please note that regardless of the type of plotting, randomization is performed in the same way. Thus, we were able to combine these two methods and create an effective simulation system for Bid and Last.

After the changes were made, the simulation became very similar to what was discussed in the article "Developing a Replay System — Market simulation (Part 13): Birth of the SIMULATOR (III)". However, we have not yet implemented random walk simulation in the system. This is because at the moment the code has been adjusted in accordance with the presented option:

inline void Simulation_LAST(const MqlRates &rate, MqlTick &tick[])
   {
      if (CheckViability_LAST(rate))
      {
      }else Random_Price(rate, tick);
      DistributeVolumeReal(rate, tick);
   }

Therefore, we do not yet model typical scenarios in which the use of a random walk would be appropriate. However, our goal is to allow the Bid price simulation to use a random walk under certain conditions in the same way that the Last price simulation does. And the question is: Is that possible? Furthermore, can we make this approach even more interesting and robust so that markets like forex can also benefit from the random walk method to simulate price movements? The answer is yes, it is possible. Before implementing a random walk specifically to construct the Last price, some changes need to be made.

inline bool CheckViability(const MqlRates &rate)
   {
#define macro_AdjustSafetyFator(A) (int)(A + ceil(A * 1.7))
                                
      int i0, i1, i2;
                                
      i0 = macro_AdjustSafetyFator((rate.high - rate.low) / m_TickSize);
      i1 = (int)((rate.open - rate.low) / m_TickSize);
      i2 = (int)((rate.high - rate.open) / m_TickSize);
      i0 += macro_AdjustSafetyFator(i1 > i2 ? i1 : i2);
      i0 += macro_AdjustSafetyFator((i1 > i2 ? (rate.high - rate.close) : (rate.close - rate.low) / m_TickSize));

      return (i0 < rate.tick_volume);
                                
#undef macro_AdjustSafetyFator
   }

The above function is an extension of the one previously used to evaluate the feasibility of generating a random walk movement. Due to technical details and the introduction of advanced safety factors, we have refined this approach so as not to mislead about the ability to perform the movement. This change is justified because the check procedure is no longer limited to just modeling the Last-based type. It is also used to evaluate the applicability of random walk in simulating Bid. At first glance, this seems simple, but it requires special precautions. To better illustrate this point, let's look at Figure 01.

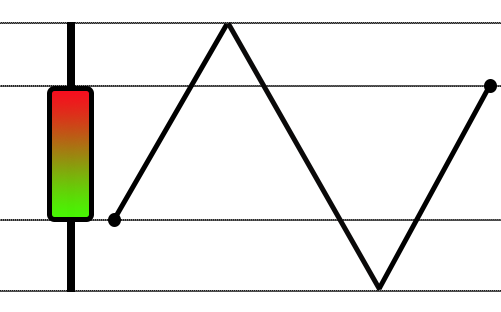
Figure 01 - Calculating the longest possible path

The function does exactly this - it calculates the longest possible way to create a 1-minute bar. This methodology has been adjusted to streamline the process so that Bid type can also benefit. Note that the safety factor increased from 1.4 to 1.7, which makes it very difficult for some assets to use random walk. The calculation begins by determining the distance between the opening price of the bar and its extremes. With this information, we use the larger value in the first step of the calculation. Another value is used to move the bar as shown in Figure 01. In the end, we make a simple calculation to check whether or not it is possible to use the random walk.

You may be thinking that we will have to make additional changes to the class code. Well, we will make changes. However, this change will be carried out in such a way as to ensure a more harmonious integration.

inline int Simulation(const MqlRates &rate, MqlTick &tick[])
   {
      m_Marks.iMax = (int) rate.tick_volume - 1;
      m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high);
      m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low);
      Simulation_Time(rate, tick);
      MountPrice(0, rate.open, rate.spread, tick);
      if (CheckViability(rate))
      {
      }else Random_Price(rate, tick);
      if (!m_IsPriceBID) DistributeVolumeReal(rate, tick);
      if (m_IsPriceBID) Random_Price(rate, tick);
      else Simulation_LAST(rate, tick);
      if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick);
      if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick);
      MountPrice(m_Marks.iMax, rate.close, rate.spread, tick);
      CorretTime(tick);

      return m_Marks.iMax;
   }

We delete the crossed-out parts and add those shown in green. There are now cases where a 1 minute bar in markets like FOREX can generate ticks similar to the stock market and vice versa. This allows the simulator to cover a wide range of market movements, regardless of tick volume. However, it is important to note that the code responsible for generating the random walk has not yet been included in the above function. Therefore, let's look at how this code would be implemented for both types of plotting, focusing specifically on this functionality.

Implementing random walk for Bid and Last prices

As discussed above, the C_Simulation class was designed to provide consistent handling between Bid and Last plotting simulations. The goal was to create as accurate a simulation as possible. We've reached a critical point where the next step is to implement a procedure that can handle random walks using the minimum amount of code required without adding complexity. This adaptation is based on what we discussed in the article "Developing a Replay System — Market simulation (Part 15): Birth of the SIMULATOR (V) - RANDOM WALK". So I won't go into detail about the original implementation of random walk or how the idea came about. For those interested in further reading, I recommend checking out the article mentioned. Here we will focus on adapting this code to a new context.

inline int RandomWalk(int In, int Out, const double Open, const double Close, double High, double Low, const int Spread, MqlTick &tick[], int iMode)
   {
      double vStep, vNext, price, vH = High, vL = Low;
      char i0 = 0;
                                
      vNext = vStep = (Out - In) / ((High - Low) / m_TickSize);
      for (int c0 = In, c1 = 0, c2 = 0; c0 <= Out; c0++, c1++)
      {
         price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -1 : 1));
         price = (price > High ? price - m_TickSize : (price < Low ? price + m_TickSize : price));
         MountPrice(c0, price, (Spread + RandomLimit((int)(Spread | (m_Marks.iMax & 0xF)), 0)), tick);
         switch (iMode)
         {
            case 0:
               if (price == Close) return c0; else break;
            case 1:
               i0 |= (price == High ? 0x01 : 0);
               i0 |= (price == Low ? 0x02 : 0);
               vH = (i0 == 3 ? High : vH);
               vL = (i0 ==3 ? Low : vL);
               break;
            default: break;
         }
         if (((int)floor(vNext)) >= c1) continue;
         if ((++c2) <= 3) continue;
         vNext += vStep;
         if (iMode != 2)
         {
            if (Close > vL) vL = (i0 == 3 ? vL : vL + m_TickSize); else vH = (i0 == 3 ? vH : vH - m_TickSize);
         }else
         {
            vL = (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize));
            vH = (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH));
         }
      }
                                
      return Out;
   }

The changes made are designed to simplify the structure of the code, while maintaining its functioning unchanged. Of particular interest here is how the previous value is read to create a new one, adapting to the type of plotting used. This flexibility is very important to the functionality of the simulator. To determine the values, we use a function already known and presented in this article, which facilitates the development of the process. As we have already said, we will not describe in detail the features of the function, since it was discussed in another article.

Now let's look at how the final function has been constructed. This is our first attempt to complete this phase of implementation while simultaneously testing whether the function designed to generate simulation calls based on bar data achieves its expected goal. The goal is to effectively cover Bid- and Last-based simulation. Below is a detailed description of the function code:

inline int Simulation(const MqlRates &rate, MqlTick &tick[])
   {
      int     i0, i1;
      bool    b0 = ((rand() & 1) == 1);
                                
      m_Marks.iMax = (int) rate.tick_volume - 1;
      m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high);
      m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low);
      Simulation_Time(rate, tick);
      MountPrice(0, rate.open, rate.spread, tick);
      if (CheckViability(rate))
      {
         i0 = (int)(MathMin(m_Marks.iMax / 3.0, m_Marks.iMax * 0.2));
         i1 = m_Marks.iMax - i0;
         i0 = RandomWalk(1, i0, rate.open, (b0 ? rate.high : rate.low), rate.high, rate.low, rate.spread, tick, 0);
         RandomWalk(i0, i1, (m_IsPriceBID ? tick[i0].bid : tick[i0].last), (b0 ? rate.low : rate.high), rate.high, rate.low, rate.spread, tick, 1);
         RandomWalk(i1, m_Marks.iMax, (m_IsPriceBID ? tick[i1].bid : tick[i1].last), rate.close, rate.high, rate.low, rate.spread, tick, 2);
	 m_Marks.bLow = m_Marks.bHigh = true;
      }else Random_Price(rate, tick);
      if (!m_IsPriceBID) DistributeVolumeReal(rate, tick);
      if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick);
      if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick);
      MountPrice(m_Marks.iMax, rate.close, rate.spread, tick);
      CorretTime(tick);

      return m_Marks.iMax;
   }

This part is responsible for simulating a random walk across bars. Although this process was used in the past, it was integrated directly into the generation code. It has now been moved to a place that makes it easier to understand and analyze, making it accessible even to novice programmers. If you take a closer look, you can see that the simulatoin system is evaluating if it is possible to use a random walk. If it is possible, the system will use it; if not, it will resort to an alternative method. Thus, we guarantee the generation of price movements or price shifts under any circumstances. This applies to both the forex market and the stock market, it doesn't matter. Our goal is to always adapt to provide the best possible simulation and equally to cover all achievable price points without deviating from what the bars show.

It is important to understand that in some situations a particular bar may not be suitable for random walk simulation, while a subsequent bar may immediately use the process. As a result, prices can vary from harmonious and smooth to more abrupt. This discrepancy does not necessarily indicate a failure in the simulation or replay system, but rather is a consequence of the need for rapid price movement on a given bar, which may not have been accompanied by significant trading volume for a smoother random walk simulation. The opposite is also true: a high trading volume may allow the use of a random walk method, which does not mean that in reality the price moved smoothly. In some cases, the movement could be sharp, but the density of traded ticks allowed us to apply a random walk in the simulation, which does not necessarily reflect the actual market conditions on that particular bar.

It may seem that we have already achieved the ideal solution, that is, our goal. But we haven't gotten there yet. Although the random walk method is widely used when the number of trades in a 1-minute bar is large, it is not applicable when the number of trades in a 1-minute bar is slightly less than necessary. Furthermore, using a completely random walk to simulate bar movement when the distance between the high and low price is close to the number of ticks results in a simulation that looks bizarre. In such cases, it is necessary to reconsider the model discussed in another article in this series, "Developing a Replay System — Market simulation (Part 11): Birth of the SIMULATOR (I)", where we proposed a system that creates a reversal inside a bar.

The idea of introducing such a system seems not only appropriate, but also possible. The goal is to generate realistic and valid movements and not trigger price values completely randomly. Therefore, the central issue is no longer time, but the value indicated in the price. Using a function that generates values without any logic, especially in situations where an experienced trader would identify logic in the price movement, is demotivating. However, this problem also has a solution. It seeks to integrate approaches from Part 11 of the series to the present. While this solution may not be immediately obvious to newbies, it is quite clear to those with more programming experience. So we won't be creating a new simulation function from scratch. We will alternate between less smooth and smoother movements, which is determined by the simulator itself. The conclusion about the movement smoothness will be based on just five pieces of information: open price, close price, high price, low price and tick volume. This is the only data needed to make this choice. So, I will not give the final solution here. My goal is to show one of the many possible ways to create and simulate movements within a 1-minute bar.

Using random walk in various scenarios – Following the least effort path

As mentioned above, you need to look for a method that includes some logic. The exclusive dependence on randomization does not give satisfactory results, even when using a 1-minute bar and using higher-period charts, such as 10 or 15 minutes. Ideally, the movements should be gradual to avoid sudden transitions from one end to the other. Thus, the movement is drawn gradually, which creates the impression of randomness, although in fact it is the result of simple mathematical calculations, creating apparent complexity. This is one of the foundations of stochastic movements.

To make the flow smarter and smoother, it is necessary to eliminate some existing function and establish rules that will direct movement in a controlled manner. Please note that we should not try to force movement in a certain direction, but we do need to define the rules for MetaTrader 5 so that it handles the process as it sees fit. To do this, we first need to modify the random walk code. The revised code is shown below:

inline int RandomWalk(int In, int Out, const double Open, const double Close, double High, double Low, const int Spread, MqlTick &tick[], int iMode, int iDesloc)
   {
      double vStep, vNext, price, vH = High, vL = Low;
      char i0 = 0;
                                
      vNext = vStep = (Out - In) / ((High - Low) / m_TickSize);
      for (int c0 = In, c1 = 0, c2 = 0; c0 <= Out; c0++, c1++)
      {
         price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -1 : 1));
         price = (price > vH ? price - m_TickSize : (price < vL ? price + m_TickSize : price));                                  
         price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -iDesloc : iDesloc));
         price = (price > vH ? vH : (price < vL ? vL : price));
         MountPrice(c0, price, (Spread + RandomLimit((int)(Spread | (m_Marks.iMax & 0xF)), 0)), tick);
         switch (iMode)
         {
            case 1:
               i0 |= (price == High ? 0x01 : 0);
               i0 |= (price == Low ? 0x02 : 0);
               vH = (i0 == 3 ? High : vH);
               vL = (i0 ==3 ? Low : vL);
               break;
            case 0:
               if (price == Close) return c0;
            default:
               break;
         }
         if (((int)floor(vNext)) >= c1) continue; else if ((++c2) <= 3) continue;
         vNext += vStep;
         vL = (iMode != 2 ? (Close > vL ? (i0 == 3 ? vL : vL + m_TickSize) : vL) : (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize)));
         vH = (iMode != 2 ? (Close > vL ? vH : (i0 == 3 ? vH : vH - m_TickSize)) : (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH)));
         if (iMode == 2)
         {
            vL = (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize));
            vH = (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH));
         }else
         {
            if (Close > vL) vL = (i0 == 3 ? vL : vL + m_TickSize); else vH = (i0 == 3 ? vH : vH - m_TickSize);
         }                                       
      }
                                
      return Out;
   }

Changes include replacing some code segments with new green additions. While the changes may seem subtle, they provide much more flexibility than the previous version. Previously, the movement was continuous, tick by tick, with no gaps in between, requiring a large volume of trades to smoothly simulate a random walk. The introduction of gaps into a 1-minute bar significantly reduces the number of necessary trades, allowing you to simulate the system with different volumes and parameters of 1-minute bars. This results in a graphical adaptation of the movement generated by the random walk when four basic values are reached: open, close, high and low. The intermediate behavior is determined by a random walk. However, the crucial aspect is the function that calls the random walk. This function is described in detail below:

inline int Simulation(const MqlRates &rate, MqlTick &tick[])
   {
      int     i0, i1, i2;
      bool    b0;
                                
      m_Marks.iMax = (int) rate.tick_volume - 1;
      m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high);
      m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low);
      Simulation_Time(rate, tick);
      MountPrice(0, rate.open, rate.spread, tick);
      if (CheckViability(rate))
      if (m_Marks.iMax > 10)
      {
         i0 = (int)(MathMin(m_Marks.iMax / 3.0, m_Marks.iMax * 0.2));
         i1 = m_Marks.iMax - i0;
         i2 = (int)(((rate.high - rate.low) / m_TickSize) / i0);
         i2 = (i2 == 0 ? 1 : i2);
         b0 = (m_Marks.iMax >= 1000 ? ((rand() & 1) == 1) : (rate.high - rate.open) < (rate.open - rate.low));
         i0 = RandomWalk(1, i0, rate.open, (b0 ? rate.high : rate.low), rate.high, rate.low, rate.spread, tick, 0, i2);
         RandomWalk(i0, i1, (m_IsPriceBID ? tick[i0].bid : tick[i0].last), (b0 ? rate.low : rate.high), rate.high, rate.low, rate.spread, tick, 1, i2);
         RandomWalk(i1, m_Marks.iMax, (m_IsPriceBID ? tick[i1].bid : tick[i1].last), rate.close, rate.high, rate.low, rate.spread, tick, 2, i2);
         m_Marks.bHigh = m_Marks.bLow = true;
      }else Random_Price(rate, tick);
      if (!m_IsPriceBID) DistributeVolumeReal(rate, tick);
      if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick);
      if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick);
      MountPrice(m_Marks.iMax, rate.close, rate.spread, tick);
      CorretTime(tick);

      return m_Marks.iMax;
   }

This function indicates that we will now no longer check the possibility of creating a random walk in the same way that we have used throughout the article. Now the evaluation takes place entirely in this function. As strange as it may seem, the system will attempt to perform a random walk with a minimum volume of only 10 trades. For volumes at or below this threshold, pure randomization will be used, which is considered more efficient than random walk in this particular context. The innovative aspect is the creation of gaps within the 1-minute bar, which is ensured by the special calculations mentioned above. For the random walk to work correctly, it is important to ensure that at least 1 tick is generated.

However, this process is not without difficulties. For random walk to be effective, additional control is required. This additional control is built by a special check, the value of which can be adjusted as needed. If the trade volume exceeds 1000 in 1 minute, the simulation system can choose a path by randomly deciding which high or low to go to first. On the other hand, if the volume is less than the set volume, the initial direction of the random walk will be determined based on the proximity of the Open price to the bar High or Low.

This method, known as the "least effort path", is effective in situations where the number of movements required is less than the total distance to be walked. This avoids choices that could lead to unnecessarily long and complex routes. Due to this computational approach, some discussions and methods proposed in this article may not appear in the final application. The following two figures illustrate the effectiveness of the system: a graph based on real tick data, and a simulation result using the least effort strategy.

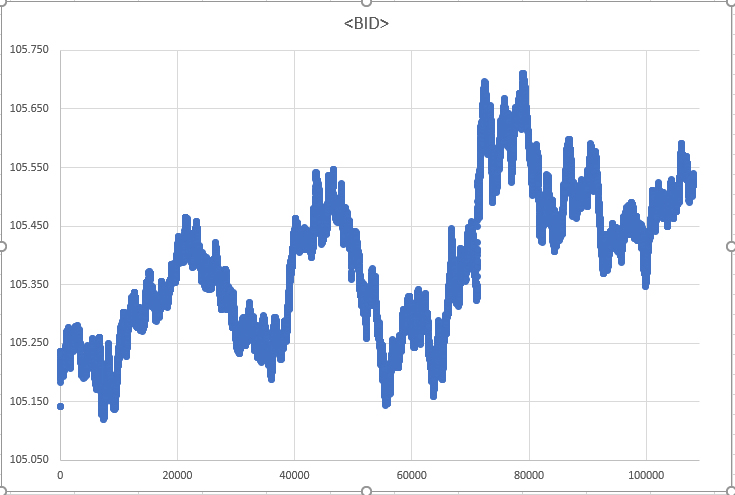
Figure 02 - Chart based on real data

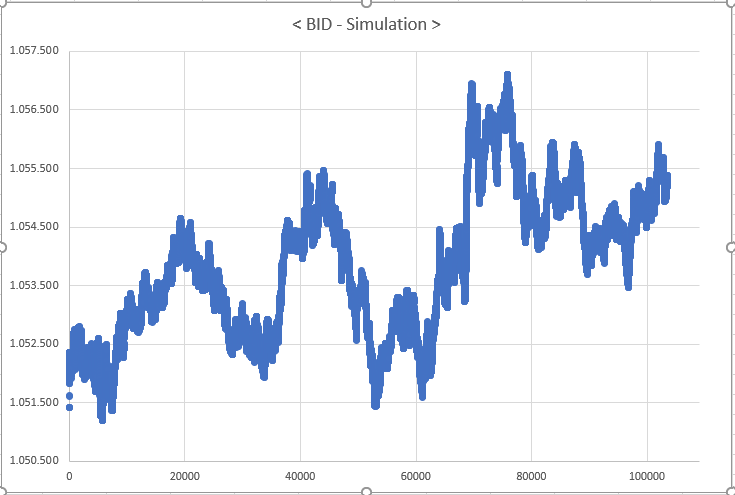
Figure 03 - Chart generated using data simulated by the system.

Although at first glance the charts may seem identical, they are not. A closer look may reveal differences, such as the data source listed in each figure to highlight the differences between them. This comparison invites users to conduct an experiment using the data presented in the application specifically for the EURUSD asset, i.e., a forex currency pair. This demonstration shows that the simulation method can be adapted to both Last and Bid plotting types, allowing the performance of the system to be tested against existing data.

Conclusion

This article is a critical step in preparing to make the replay/simulation system fully functional. In the next article, we'll look at the final settings required before moving on to describe the replay/simulation service further. This stage is important for those who seek to understand the performance and effectiveness of the system under testing conditions.

An important note about the attached files: Due to the large data size, especially when it comes to real ticks for future assets, I will provide four files, each associated with a specific asset or market. The main file includes the source code of the system up to the current state of development. To ensure the integrity of the system structure and functionality, all files must be downloaded and saved in the directory specified by the MQL5 editor.