
开发回放系统 — 市场模拟(第 24 部分):外汇(V)
概述
在上一篇文章《开发回放系统 — 市场模拟(第 23 部分):外汇(IV)》中,我们视察了模拟系统部分阻塞的实现。该模块是必要的,因为系统在应对极低的业务量时遇到了困难。当尝试基于“最后成交价”绘制类型运行模拟时,该限制变得明显,在尝试生成模拟时,系统有崩溃的风险。若 1-分钟柱线呈现的交易量不足之时,这个问题尤为引人注目。为了解决这个问题,今天我们将视察如何适配实现,并遵循以前基于出价绘制模拟的所用原则。这种方式在外汇市场中被广泛采用,所以这已经是有关该主题的第五篇文章了。但在这种情况下,我们不会特别关注货币,因为我们的目标是改进股票市场模拟系统。
我们开始实现修改
第一步是在我们的类中引入一个私密结构。这是因为我们拥有的数据可在“最后成交价”和“出价”两种模拟模式下公用。这些公用元素本质上是数值,将被组合成为一个单一的结构。故此,我们定义了以下结构:
struct st00 { bool bHigh, bLow; int iMax; }m_Marks;
虽然这看起来像是一个简单的结构,但它足够健壮,可令我们改进代码。将所有共用数值收集到一个地方,我们极大提高了我们的工作效率。
完成准备后,我们就可开始针对代码进行第一次真正的修改。
inline int Simulation(const MqlRates &rate, MqlTick &tick[]) { m_Marks.iMax = (int) rate.tick_volume - 1; m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high); m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low); Simulation_Time(rate, tick); if (m_IsPriceBID) Simulation_BID(rate, tick); else Simulation_LAST(rate, tick); else return -1; CorretTime(tick); return m_Marks.iMax; }
今天,我们将去除阻止基于最后成交价进行模拟的限制,并将专门针对这类模拟引入一个新的切入点。整个操作机制将基于外汇市场的原则。该过程的主要区别在于出价(Bid)和最后成交价(Last)模拟的分离。不过,重点要注意,用于随机化时间,并将其调整为与 C_Replay 类兼容的方法在两类模拟中保持雷同。这种一致性很不错,因为如果我们更改其中一种模式,另一种模式也会受益,尤其是在管理跳价之间的时间之时。自然,此处讨论的修改也会影响基于出价绘制类型的模拟。这些变化相当容易理解,故我不会深入细节。
我们回到我们的目标代码。一旦我们加上调用基于最后成交价的模拟函数,我们就能看到这个调用的第一点。以下是该函数的内部结构:
inline void Simulation_LAST(const MqlRates &rate, MqlTick &tick[]) { if (CheckViability_LAST(rate)) { }else { } DistributeVolumeReal(rate, tick); }
在这个上下文里,我们按最后成交价绘制时要执行两个重要步骤。第一步是测试使用随机游走系统进行仿真的可能性,如前几篇文章讨论的那样。对于那些没有研究过这个话题的人,我建议阅读文章《开发回放系统 — 市场模拟(第 15 部分):模拟器的诞生(V)- 随机游走》。第二步是在可能的跳价之间配发交易量。在基于最后成交价绘制类型操控仿真时,这些步骤非常重要。
在详细描述结构之前,我们先看一下基于最后成交价模拟的两个关键函数。第一个函数如下所示:
inline bool CheckViability_LAST(const MqlRates &rate) { #define macro_AdjustSafetyFator(A) (A + (A * 1.4)); double v0, v1, v2; v0 = macro_AdjustSafetyFator(rate.high - rate.low); v1 = (rate.open - rate.low); v2 = (rate.high - rate.open); v0 += macro_AdjustSafetyFator(v1 > v2 ? v1 : v2); v1 = (rate.close - rate.low); v2 = (rate.high - rate.close); v0 += macro_AdjustSafetyFator(v1 > v2 ? v1 : v2); return ((int)(v0 / m_TickSize) < rate.tick_volume); #undef macro_AdjustSafetyFator }
该函数负责检查在可用限制内生成随机游走的可能性。它是如何完成的?该方法判定当前可用的跳价数量。这些信息由我们将要操控的柱线提供,其中的跳价数量我们需要涵盖,然后在函数中计算。
注意,我们不会直接用该数值来判定要覆盖的区域。这是因为如果我们用此直接方式,由此产生的随机游走看起来是人为的,很容易预测其走势。为了缓解这个问题,我们将调整计算。此设置利用宏实现,定义了一个大 30% 的区域,其作用是充当正确生成随机游走的保险系数。另一个重要方面是需要始终在计算中考虑最大可能的距离,因为随机化也许需要这样的扩张。因此,在计算过程中已经考虑了这种可能性。
最终结果表明是否适合使用随机游走方式,或是应当采用另一种更直接的随机化方法。不过,该决定是由调用过程做出的,而不是在此处。
下面我们详细讲述第二个函数:
inline void DistributeVolumeReal(const MqlRates &rate, MqlTick &tick[]) { for (int c0 = 0; c0 <= m_Marks.iMax; c0++) tick[c0].volume_real = 1.0; for (int c0 = (int)(rate.real_volume - rate.tick_volume); c0 > 0; c0--) tick[RandomLimit(0, m_Marks.iMax)].volume_real += 1.0; }
此处的目标是把交易总量随机分配在 1-分钟柱线上。第一个循环执行主要分配,确保每个跳价都收到最小的初始交易量。第二个循环负责随机分配剩余交易量,防止其集中在一次跳价当中。尽管这种可能性仍然存在,但所采用的分配方法将其极大降低。
这些函数已经是原始实现的一部分,并在有关随机游走实现的文章中讨论过了。然而,这一次我们采用了更加模块化的方式,最大限度地提高已开发代码的可重用性。
经过进一步的反思,我们确定了在出价和最后成交价模拟中仍然保留共用元素。其中包括入场点和离场点的定义,以及定义终点的能力。鉴于这一点,我们努力重用以前开发的代码。为此,我们需要修改上一篇文章中出现过的代码。修改如下:
inline void Mount_BID(const int iPos, const double price, const int spread, MqlTick &tick[]) inline void MountPrice(const int iPos, const double price, const int spread, MqlTick &tick[]) { if (m_IsPriceBID) { tick[iPos].bid = price; tick[iPos].ask = NormalizeDouble(price + (m_TickSize * spread), m_NDigits); }else tick[iPos].last = NormalizeDouble(price, m_NDigits); }
我们首先用新名称替换旧的函数名称,然后插入一个内部测试来判定模拟是基于出价还是最后成交价绘制类型。因此,根据 1-分钟柱线文件中可观测数据,相同的函数可适配为基于出价或最后成交价生成跳价。
此修改还需要两项调整。我们的目标是以简化的方式把出价和最后成交价模拟集成到一起,如此相应方法仅处理真正独特的方面。其它要点则按普通基本处理。以下是在模拟类代码中的修改:
inline void Simulation_BID(const MqlRates &rate, MqlTick &tick[]) { Mount_BID(0, rate.open, rate.spread, tick); for (int c0 = 1; c0 < m_Marks.iMax; c0++) { Mount_BID(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick); MountPrice(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick); m_Marks.bHigh = (rate.high == tick[c0].bid) || m_Marks.bHigh; m_Marks.bLow = (rate.low == tick[c0].bid) || m_Marks.bLow; } if (!m_Marks.bLow) Mount_BID(Unique(rate.high, tick), rate.low, rate.spread, tick); if (!m_Marks.bHigh) Mount_BID(Unique(rate.low, tick), rate.high, rate.spread, tick); Mount_BID(m_Marks.iMax, rate.close, rate.spread, tick); }
划掉的行是被删除了,确保代码继续正常运行。不过,为了整个仿真系统的共用形式,我们还需要这些划掉的部分显示最后成交价。于是这部分共用代码被转移到了下面的函数之中:
inline int Simulation(const MqlRates &rate, MqlTick &tick[]) { m_Marks.iMax = (int) rate.tick_volume - 1; m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high); m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low); Simulation_Time(rate, tick); MountPrice(0, rate.open, rate.spread, tick); if (m_IsPriceBID) Simulation_BID(rate, tick); else Simulation_LAST(rate, tick); if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick); if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick); MountPrice(m_Marks.iMax, rate.close, rate.spread, tick); CorretTime(tick); return m_Marks.iMax; }
现在我们来到决定性的时刻。在没有重大变更的情况下,仅通过智能代码重用,我们就能够集成这两种模拟。因此,我们现在有一个基于出价和最后成交价绘制类型的模拟。如果之前未在随机模拟中指定,则我们会自动包括输入、输出和极限值。配合这一策略调整,我们就明显扩展了模拟系统的范围。此外,并没有增加代码的复杂度,代码本身也没有太多增长。如果您使用截至目前提供的代码,您会得到基于出价模拟的优秀性能。您能够在图表上至少能按最后成交价绘制类型播放一根柱线。好吧,最小值将是错误的,因为它会为零,即使它是按正确数值定义的。这是因为对于仅有定义时间的未初始化跳价,所有“最后成交价”数值都等于零。若非我们已分配了交易量,这不是啥问题。故此,我们回到我们的函数,其将最后成交价放入每次跳价之中。我们需要提供具有正确数据的模拟。
我们的最后价格模拟功能保持不变。不过,在查看出价模拟代码时,会浮现一个想法:我们是否可以用相同代码来模拟最后成交价,尤其是在跳价数量不足以完全执行随机游走的情况下?我也有此疑问。经过精心分析,我们得出结论,只需要对出价建模函数进行略微的修改。不过,为了避免将来我们必须修改代码时出现混淆,我们现在需要精心计划这些修改。出价模拟过程由刚才提到的函数启动。鉴于最后成交价模拟概念类似,我们可以寻找一种途径来保持之前调用不变。因此,我们适配出价模拟函数,如此在未应用随机游走的情况下,它也可以涵盖最后成交价模拟。
有些人可能会质疑这种方法,但此处是模拟代码如何适配出价绘制,从而包括基于最后成交价绘制模拟。
inline void Simulation_BID(const MqlRates &rate, MqlTick &tick[]) inline void Random_Price(const MqlRates &rate, MqlTick &tick[]) { for (int c0 = 1; c0 < m_Marks.iMax; c0++) { MountPrice(c0, NormalizeDouble(RandomLimit(rate.high, rate.low), m_NDigits), (rate.spread + RandomLimit((int)(rate.spread | (m_Marks.iMax & 0xF)), 0)), tick); m_Marks.bHigh = (rate.high == (m_IsPriceBID ? tick[c0].bid : tick[c0].last)) || m_Marks.bHigh; m_Marks.bLow = (rate.low == (m_IsPriceBID ? tick[c0].bid : tick[c0].last)) || m_Marks.bLow; m_Marks.bHigh = (rate.high == tick[c0].bid) || m_Marks.bHigh; m_Marks.bLow = (rate.low == tick[c0].bid) || m_Marks.bLow; } }
为了避免运行时混淆,我决定重命名该函数。为了获得更通用代码的益处,而付出的代价很小。这种改编的思路如下。这两段代码元素值得特别注意。三元运算符虽然被一些人认为晦涩难懂,但它是 C 语言的宝贵遗产,它提供了许多有用的东西。这些片段检查绘制类型,并相应调整价格。请注意,无论绘制类型如何,随机化都按相同的方式执行。因此,我们能够将这两种方法结合起来,并为出价和最后成交价创建一个高效的模拟系统。
修改之后,模拟变得与《开发回放系统 — 市场模拟(第 13 部分):模拟器的诞生(III)》一文中讨论的内容非常相似。不过,我们尚未在系统中实现随机游走模拟。这是因为目前代码已根据提供的选项进行了调整:
inline void Simulation_LAST(const MqlRates &rate, MqlTick &tick[]) { if (CheckViability_LAST(rate)) { }else Random_Price(rate, tick); DistributeVolumeReal(rate, tick); }
因此,我们尚未针对适合运用随机游走的典型场景进行建模。不过,我们的目标是允许出价模拟在特定条件下使用随机游走,就如最后成交价模拟一样的方式。问题是:这可能吗?甚至,我们能否令这种方式更有趣和健壮,如此像外汇这样的市场,也可受益于按随机游走方法模拟价格走势?答案是肯定的,这是可能的。在专门按最后成交价实现随机游走构造之前,需要进行一些修改。
inline bool CheckViability(const MqlRates &rate) { #define macro_AdjustSafetyFator(A) (int)(A + ceil(A * 1.7)) int i0, i1, i2; i0 = macro_AdjustSafetyFator((rate.high - rate.low) / m_TickSize); i1 = (int)((rate.open - rate.low) / m_TickSize); i2 = (int)((rate.high - rate.open) / m_TickSize); i0 += macro_AdjustSafetyFator(i1 > i2 ? i1 : i2); i0 += macro_AdjustSafetyFator((i1 > i2 ? (rate.high - rate.close) : (rate.close - rate.low) / m_TickSize)); return (i0 < rate.tick_volume); #undef macro_AdjustSafetyFator }
上述函数是之前用来估测生成随机游走走势可行性函数的扩展。由于技术细节和引入的高级安全因素,我们改进了这种方式,这样就不会误入歧途。此修改是合理的,因为检查过程不再局限于仅对基于最后成交价类型进行建模。它还用于评估随机游走在模拟出价中的适用性。初看,这看似很简单,但需要特殊的预防措施。为了更好地概括这一点,我们看一下图例 01。
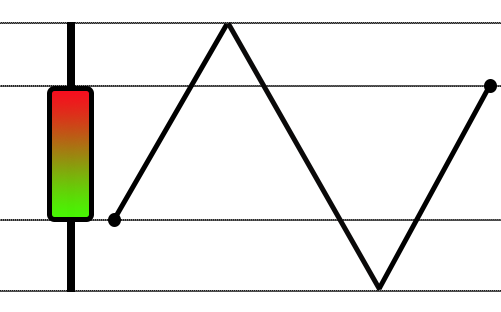
图例 01 - 计算最长可能路径
该函数正是这样做的 — 它计算创建 1-分钟柱线的最长可能途径。该方法已被调整,简化了流程,如此出价类型也能受益。注意,保险系数从 1.4 增加到 1.7,这令某些资产很难运用随机游走。计算首先判定柱线的开盘价与其极值之间的距离。依据这些信息,我们在计算的第一步中取用较大值。另一个值用于移动柱线,如图例 01 所示。在末尾,我们做一个简单的计算来检查是否可以使用随机游走。
您也许认为我们会对类代码进行其它修改。好吧,我们会做出改变。不过,这种变化将以确保更和谐的集成的方式运作。
inline int Simulation(const MqlRates &rate, MqlTick &tick[]) { m_Marks.iMax = (int) rate.tick_volume - 1; m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high); m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low); Simulation_Time(rate, tick); MountPrice(0, rate.open, rate.spread, tick); if (CheckViability(rate)) { }else Random_Price(rate, tick); if (!m_IsPriceBID) DistributeVolumeReal(rate, tick); if (m_IsPriceBID) Random_Price(rate, tick); else Simulation_LAST(rate, tick); if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick); if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick); MountPrice(m_Marks.iMax, rate.close, rate.spread, tick); CorretTime(tick); return m_Marks.iMax; }
我们把划掉的部分删除,并加上绿色显示的部分。现在,某些情况下,外汇等市场的 1-分钟柱线可以产生类似于股票市场的跳价,反之亦然。这令模拟器能够覆盖更广泛的市场走势,无关跳价交易量。不过,重点要注意,负责生成随机游走的代码尚未包含在上述函数当中。因此,我们看看如何实现这两种类型的绘制代码,尤其关注此功能性。
针对出价和最后成交价实现随机游走
如上所述,C_Simulation 类设计用于为出价和最后成交价绘制模拟之间提供一致的处理。目标是创建尽可能准确的模拟。我们已经到达了一个临界点,下一步是实现一个过程,能用最少代码量处理随机游走,而无需增加复杂度。这种适配基于我们在文章《开发回放系统 — 市场模拟(第 15 部分):模拟器的诞生(V)- 随机游走》中讨论的内容。因此,我不会详述随机游走的原始实现,或这个思路是如何得来的。若有有兴趣进一步阅读,我建议查看提到的文章。在此,我们把重点放在如何令此代码适配新的上下文。
inline int RandomWalk(int In, int Out, const double Open, const double Close, double High, double Low, const int Spread, MqlTick &tick[], int iMode) { double vStep, vNext, price, vH = High, vL = Low; char i0 = 0; vNext = vStep = (Out - In) / ((High - Low) / m_TickSize); for (int c0 = In, c1 = 0, c2 = 0; c0 <= Out; c0++, c1++) { price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -1 : 1)); price = (price > High ? price - m_TickSize : (price < Low ? price + m_TickSize : price)); MountPrice(c0, price, (Spread + RandomLimit((int)(Spread | (m_Marks.iMax & 0xF)), 0)), tick); switch (iMode) { case 0: if (price == Close) return c0; else break; case 1: i0 |= (price == High ? 0x01 : 0); i0 |= (price == Low ? 0x02 : 0); vH = (i0 == 3 ? High : vH); vL = (i0 ==3 ? Low : vL); break; default: break; } if (((int)floor(vNext)) >= c1) continue; if ((++c2) <= 3) continue; vNext += vStep; if (iMode != 2) { if (Close > vL) vL = (i0 == 3 ? vL : vL + m_TickSize); else vH = (i0 == 3 ? vH : vH - m_TickSize); }else { vL = (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize)); vH = (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH)); } } return Out; }
所做的修改旨在简化代码的结构,同时保持其功能不变。此处特感兴趣的是如何读取前一个数值,以便创建一个新值,并适配所用的绘制类型。这种灵活性对于模拟器的功能非常重要。为了判定这些数值,我们用到一个已知并在本文中讲解过的函数,其有助于该过程的开发。正如我们已经说过的,我们不会详述该函数的功能,因为它在另一篇文章中已经讨论过。
现在我们看看最终函数是如何构造的。这是我们首次尝试完成这一阶段的实现,同时测试基于柱线数据生成模拟的函数调用是否实现了其预期目标。目标是有效地涵盖基于出价和最后成交价的模拟。以下是函数代码的详细说明:
inline int Simulation(const MqlRates &rate, MqlTick &tick[]) { int i0, i1; bool b0 = ((rand() & 1) == 1); m_Marks.iMax = (int) rate.tick_volume - 1; m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high); m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low); Simulation_Time(rate, tick); MountPrice(0, rate.open, rate.spread, tick); if (CheckViability(rate)) { i0 = (int)(MathMin(m_Marks.iMax / 3.0, m_Marks.iMax * 0.2)); i1 = m_Marks.iMax - i0; i0 = RandomWalk(1, i0, rate.open, (b0 ? rate.high : rate.low), rate.high, rate.low, rate.spread, tick, 0); RandomWalk(i0, i1, (m_IsPriceBID ? tick[i0].bid : tick[i0].last), (b0 ? rate.low : rate.high), rate.high, rate.low, rate.spread, tick, 1); RandomWalk(i1, m_Marks.iMax, (m_IsPriceBID ? tick[i1].bid : tick[i1].last), rate.close, rate.high, rate.low, rate.spread, tick, 2); m_Marks.bLow = m_Marks.bHigh = true; }else Random_Price(rate, tick); if (!m_IsPriceBID) DistributeVolumeReal(rate, tick); if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick); if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick); MountPrice(m_Marks.iMax, rate.close, rate.spread, tick); CorretTime(tick); return m_Marks.iMax; }
这部分负责模拟跨柱线的随机游走。虽然该过程过去曾用过,它已直接集成到生成代码之中。它现在已被移至一个更容易理解和分析的地方,即使萌新程序员也可以访问它。如果您仔细观察,能够看到模拟系统正在评估是否有使用随机游走的可能。如果可能,系统就会用它;如果不行,它将诉诸替代方法。因此,我们保证在任何境况下都会产生价格走势或价格位移。把其应用于外汇市场和股票市场,都无所谓。我们的目标是一直适配,从而提供最佳模拟,涵盖所有可达成的价格点,而不会自柱线所示偏离。
重要的是要明白,在某些状况下,特定柱线可能不适合随机游走模拟,而后续柱线也许会立即用到该过程。结果就是,价格会从和谐和平稳,变得更急剧。这种矛盾并不一定表明模拟或回放系统出现故障,而是给定柱线需要快速价格走势,这对于较平滑的随机行走模拟来说也许没有伴随明显的交易量。反之亦然:高交易量也许能使用随机游走方法,而这并不意味着实际价格移动平稳。在某些情况下,走势可能很剧烈,但交易跳价的密度允许我们在模拟中应用随机游走,这并不一定反映该特定柱线的实际市场状况。
我们看似已经达成了理想的解决方案,即我们的目标。但我们还未得到所有。虽然在 1-分钟柱线中的交易数量较大时,随机游走方法被广泛使用,但当 1-分钟柱线中的交易数量略少于必要值时,它就不再适用。甚而,当最高价和最低价之间的距离接近跳价数量时,使用完全随机游走来模拟柱线走势会导致模拟看起来很怪异。在这种情况下,有必要重温本系列的另一篇文章《开发回放系统 — 市场模拟(第 11 部分):模拟器的诞生(I)》中讨论过的模型,其中我们提出了一个系统能在柱内创建逆转。
引入这样一个系统的思路看似不仅合适、而且是可能的。目标是产生现实和有效的走势,且不会完全随机地触发价格值。因此,中心问题不再是时间,而是价格中指示的数值。在没有任何逻辑的情况下用函数生成一个数值,尤其是在经验丰富的交易者能识别价格走势中的逻辑的情况下,是令人沮丧的。不过,这个问题也有解决方案。它寻求现在就把来自本系列第 11 部分的方法整合。虽然这个解决方案对于萌新来说也许并非立竿见影,但对于那些有更多编程经验的人来说却是很清晰的。因此,我们不会从头开始创建新的模拟函数。我们将在不太平滑和更平滑的走势之间交替,这是由模拟器本身判定的。关于走势平滑度的结论将仅基于五条信息:开盘价、收盘价、最高价、最低价、和跳价交易量。这是做出此选择所需的唯一数据。因此,我不会在此给出最终方案。我的目标是展示在 1-分钟柱线内创建和模拟走势的众多可能方式之一。
在各种场景中使用随机游走 — 遵循最省力的路径
如上所述,您需要寻找一种包含一些逻辑的方法。光靠随机化并不能给出令人满意的结果,即便使用 1-分钟柱线,以及使用更高周期的图表,例如 10 或 15 分钟。理想情况下,走势应该是渐进的,从而避免从一端到另一端的剧烈转变。因此,走势是逐渐绘制的,这给人一种随机性的印象,尽管实际上它是简单数学计算的结果,产生了明显的复杂性。这是随机走势的基本面之一。
为了令流程更智能、更顺畅,有必要剔除一些已有函数,并按可控方式建立指导走势的规则。请注意,我们不应该试图强制走势往某个方向发展,但我们确实需要定义 MetaTrader 5 的规则,如此它就可按照适合的方式处理该过程。为此,我们首先需要修改随机游走代码。修改后的代码如下所示:
inline int RandomWalk(int In, int Out, const double Open, const double Close, double High, double Low, const int Spread, MqlTick &tick[], int iMode, int iDesloc) { double vStep, vNext, price, vH = High, vL = Low; char i0 = 0; vNext = vStep = (Out - In) / ((High - Low) / m_TickSize); for (int c0 = In, c1 = 0, c2 = 0; c0 <= Out; c0++, c1++) { price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -1 : 1)); price = (price > vH ? price - m_TickSize : (price < vL ? price + m_TickSize : price)); price = (m_IsPriceBID ? tick[c0 - 1].bid : tick[c0 - 1].last) + (m_TickSize * ((rand() & 1) == 1 ? -iDesloc : iDesloc)); price = (price > vH ? vH : (price < vL ? vL : price)); MountPrice(c0, price, (Spread + RandomLimit((int)(Spread | (m_Marks.iMax & 0xF)), 0)), tick); switch (iMode) { case 1: i0 |= (price == High ? 0x01 : 0); i0 |= (price == Low ? 0x02 : 0); vH = (i0 == 3 ? High : vH); vL = (i0 ==3 ? Low : vL); break; case 0: if (price == Close) return c0; default: break; } if (((int)floor(vNext)) >= c1) continue; else if ((++c2) <= 3) continue; vNext += vStep; vL = (iMode != 2 ? (Close > vL ? (i0 == 3 ? vL : vL + m_TickSize) : vL) : (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize))); vH = (iMode != 2 ? (Close > vL ? vH : (i0 == 3 ? vH : vH - m_TickSize)) : (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH))); if (iMode == 2) { vL = (((c2 & 1) == 1) ? (Close > vL ? vL + m_TickSize : vL) : (Close < vH ? vL : vL + m_TickSize)); vH = (((c2 & 1) == 1) ? (Close > vL ? vH : vH - m_TickSize) : (Close < vH ? vH - m_TickSize : vH)); }else { if (Close > vL) vL = (i0 == 3 ? vL : vL + m_TickSize); else vH = (i0 == 3 ? vH : vH - m_TickSize); } } return Out; }
修改包括由新加的绿色行替换某些代码段。虽然这些变化也许看起来很微妙,但它们提供了比以前版本更多的灵活性。以前,走势是连续的,跳价一个接一个,之间没有空隙,模拟平滑的随机游走需要大量的交易。在 1-分钟柱线中引入空隙可明显降低必要的交易数量,允许您依据不同交易量和 1-分钟柱线参数模拟系统。当四个基本数值到达时(开盘价、收盘价、最高价、和最低价),会由随机游走生成适配的走势图形结果。过渡行为由随机游走判定。然而,关键的层面是随机游走调用的函数。下面详细讲述了该函数:
inline int Simulation(const MqlRates &rate, MqlTick &tick[]) { int i0, i1, i2; bool b0; m_Marks.iMax = (int) rate.tick_volume - 1; m_Marks.bHigh = (rate.open == rate.high) || (rate.close == rate.high); m_Marks.bLow = (rate.open == rate.low) || (rate.close == rate.low); Simulation_Time(rate, tick); MountPrice(0, rate.open, rate.spread, tick); if (CheckViability(rate)) if (m_Marks.iMax > 10) { i0 = (int)(MathMin(m_Marks.iMax / 3.0, m_Marks.iMax * 0.2)); i1 = m_Marks.iMax - i0; i2 = (int)(((rate.high - rate.low) / m_TickSize) / i0); i2 = (i2 == 0 ? 1 : i2); b0 = (m_Marks.iMax >= 1000 ? ((rand() & 1) == 1) : (rate.high - rate.open) < (rate.open - rate.low)); i0 = RandomWalk(1, i0, rate.open, (b0 ? rate.high : rate.low), rate.high, rate.low, rate.spread, tick, 0, i2); RandomWalk(i0, i1, (m_IsPriceBID ? tick[i0].bid : tick[i0].last), (b0 ? rate.low : rate.high), rate.high, rate.low, rate.spread, tick, 1, i2); RandomWalk(i1, m_Marks.iMax, (m_IsPriceBID ? tick[i1].bid : tick[i1].last), rate.close, rate.high, rate.low, rate.spread, tick, 2, i2); m_Marks.bHigh = m_Marks.bLow = true; }else Random_Price(rate, tick); if (!m_IsPriceBID) DistributeVolumeReal(rate, tick); if (!m_Marks.bLow) MountPrice(Unique(rate.high, tick), rate.low, rate.spread, tick); if (!m_Marks.bHigh) MountPrice(Unique(rate.low, tick), rate.high, rate.spread, tick); MountPrice(m_Marks.iMax, rate.close, rate.spread, tick); CorretTime(tick); return m_Marks.iMax; }
该函数表明,我们现在将不再按照通篇文章所用相同的方式检查创建随机游走的可能性。现在,评估在该函数整体中进行。也许看起来很奇怪,但系统将尝试执行随机游走,仅有 10 笔最小交易量的交易。对于等于或低于此阈值的交易量,将使用纯粹的随机化,在这种特殊的前后呼应环境中,会认为这样做比随机游走更有效。创新层面是在 1-分钟柱线内创建空隙,这是由上述特殊计算来确保的。为了令随机游走正常工作,重要的是确保至少生成 1 次跳价。
然而,这个过程并非没有困难。为了令随机游走有效,需要额外的控制。额外控制由特殊检查构建,其值可根据需要进行调整。如果交易量在 1 分钟内超过 1000,模拟系统可以随机决定选择路径,即先去高点亦或低点。另一方面,如果交易量小于设定的阈值,则随机游走的初始方向将根据开盘价与柱线高点或低点的接近程度来判定。
这种方法被称为“最省力路径”,这在所需的走势次数少于游走总距离的情况下是有效的。这避免了可能导致不必要的漫长和复杂路线。由于这种计算方法,本文中拟议的一些论点和方法也许不会出现在最终应用程序之中。以下两张图例概括了该系统的有效性:基于真实跳价数据的图表,以及运用最省力策略的模拟结果。
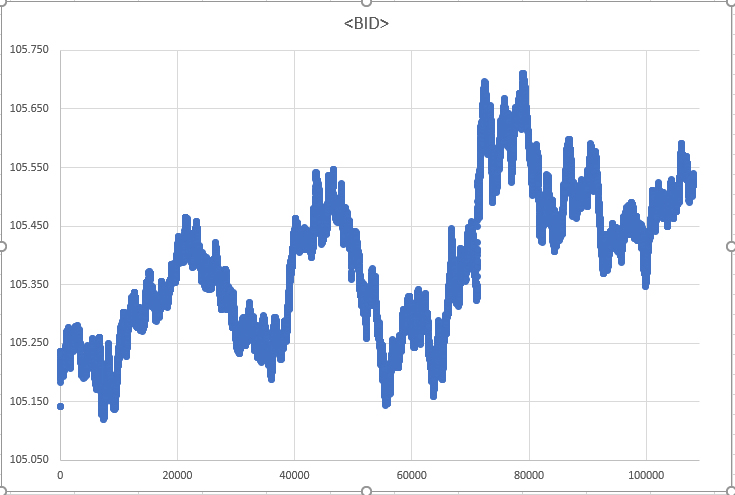
图例 02 - 基于真实数据的图表
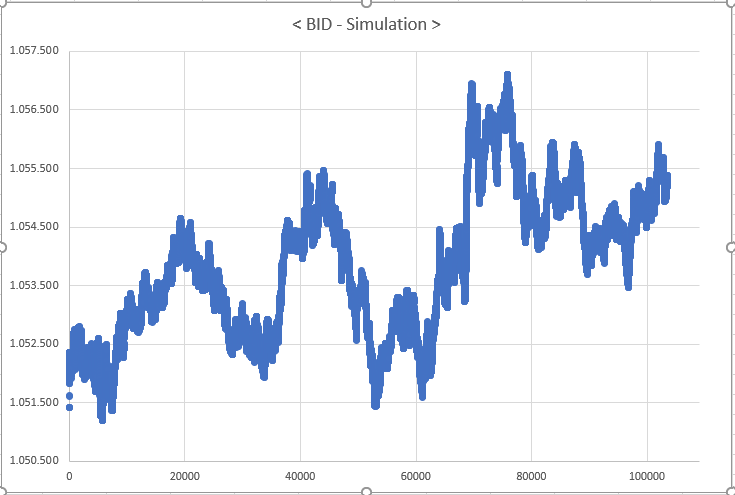
图例 03 - 由系统模拟生成的数据图表。
虽然乍一看,这些图表看似完全相同,但事实并非如此。仔细观察也许会发现差异,例如每个图例中列出的数据源,强调了它们之间的差异。可以邀请用户来比较,依据应用程序中专门针对 EURUSD 资产(即外汇货币对)提供的数据进行实验。该演示表明,模拟方法可以适配最后成交价和出价两者绘制类型,从而可以基于现有数据测试系统的性能。
结束语
本文是回放/模拟系统完全发挥作用的关键准备步骤。在下一篇文章中,我们在转入进一步讲述回放/模拟服务之前,将先视察所需的最终设置。对于那些寻求理解系统在测试条件下的性能和有效性的人来说,这个阶段很重要。
关于附件的重要说明:由于数据量庞大,尤其是在涉及未来资产的真实跳价时,我将提供四个文件,每个文件都与特定资产或市场相关联。主文件包括系统的源代码,直至当前的开发状态。为了确保系统结构和功能的完整性,所有文件都必须下载,并保存在 MQL5 编辑器指定的目录当中。
本文由MetaQuotes Ltd译自葡萄牙语
原文地址: https://www.mql5.com/pt/articles/11189
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。