Das Phänomen St. Petersburg. Die Paradoxien der Wahrscheinlichkeitsrechnung. - Seite 2

Neuer Kommentar
 
Vitalii Ananev:

:) Das gleiche Schema wurde in der Vergangenheit von Gaunern verwendet, und es wird wahrscheinlich auch jetzt von Gaunern verschiedener Couleur verwendet werden. Das Wichtigste für sie ist, dass das Opfer das Geld aushändigt, und sie werden es nie zurückbekommen.

Und einmal war ich auf einem Automarkt in Yuzhny Port, als sie einen Trottel für drei Karten "mitnahmen"...

Das ist ziemlich schwer zu sagen. Irgendwann war ich sicher, dass der Trottel gewinnen würde...

Danach fuhr ich eines Tages spät nach Hause. Es gibt nur sehr wenige Menschen außerhalb der U-Bahn... ...und da sitzen ein paar Typen und werfen mit diesen drei Karten um sich. Ich greife sie auf und erzähle ihnen kurz die Geschichte, gefolgt von der Frage: "Wie machst du das?". Es stellt sich heraus, dass es ganz einfach ist. Alle Karten haben einen Wisch mit dem kleinen Finger, um eine Ecke zu biegen, die der Geber nicht gesehen hat... ...aber in Wirklichkeit hat er die Ecke einer anderen Karte umgedreht, und die Karte, die von einem falschen Spieler umgedreht wurde, hat er wieder aufgedeckt.

  
//+------------------------------------------------------------------+
//|                                                          SPp.mq5 |
//|                        Copyright 2017, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//--- input parameters
input int      bet=4;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart(){
   
   double me=0;
   double bank=0;
   
   while(!IsStopped()){
      
      
      double z=1.0;
      
      while(!IsStopped()){
         if(MathRand()/32768.0<0.5){
            // I win
            z=MathMin(bet,z);
            me+=z;
            bank+=(bet-z);
            break;
         }
         else{
            z*=2.0;
         }
      }
      
      Comment("Me: ",(string)me,", bank: ",(string)bank);
   
   }
   
   Comment("");

}

Bei einem Einsatz von 4 scheint es sich um ein gleiches Spielfeld zu handeln (wenn ich die Spielregeln richtig verstehe).

 
Alexey Viktorov:

Und ich habe einmal beobachtet, wie ein Trottel auf einem Automarkt in South Port für drei Karten "eingekauft" wurde...

Das ist ziemlich schwer zu sagen. Irgendwann war ich sicher, dass der Trottel gewinnen würde...

Danach fuhr ich eines Tages spät nach Hause. Es gibt nur sehr wenige Menschen außerhalb der U-Bahn... ...und da sitzen diese Typen und werfen mit diesen drei Karten umher. Ich greife sie auf und erzähle ihnen kurz die Geschichte, gefolgt von der Frage: "Wie machst du das?". Es stellt sich heraus, dass es ganz einfach ist. Alle Karten haben einen Wisch mit dem kleinen Finger, um eine Ecke zu biegen, die der Geber nicht gesehen hat... ...aber in Wirklichkeit hat er die Ecke einer anderen Karte umgedreht, und die Karte, die von einem falschen Spieler umgedreht wurde, ist nicht umgedreht.

Eigentlich ist es viel einfacher als das. Um die "Trage" herum reiben sich immer seine Assistenten, auch bekannt als die Anrufer, sie spielen auch, manchmal gewinnen sie, manchmal verlieren sie. Im Allgemeinen erwecken sie den Anschein von Fairplay. Eine beliebige Person, die bei diesem Spiel eine Wette abschließt, bekommt ihr Geld nicht zurück, selbst wenn sie richtig liegt. Egal, ob es sich um 3 Karten oder 3 Gläser und einen Ball handelt, sobald ein Spieler eine Karte aufdeckt oder ein Glas hebt, beugen sich diese Helfer angeblich vor, um genauer hinzuschauen, und versperren so die Sicht von zufälligen Zeugen. Wenn der Spieler es erraten hat, kann er es einfach anfechten und sagen: Nein, das hast du nicht. Wenn ein "Trottel" sehr entrüstet ist, kann er ihm sogar in den Nacken treten. Der "Katala" selbst muss sich nicht einmal anstrengen, um den Spieler zu verwirren, seine Aufgabe ist es, den Einsatz zu erhalten.

 
Novaja:
Das Phänomen St. Petersburg
Es ist wie das Radio, das angeblich von Popov erfunden wurde.

das übliche Martingal...
 
hartmann:
Es ist wie das Radio, das angeblich von Popov erfunden wurde.

ein normales Martingal...

Ungewöhnlich

 
Vitalii Ananev:

In Wirklichkeit ist es viel einfacher als das. Um die "Trage" herum befinden sich immer seine Assistenten, die so genannten "Baiters", die ebenfalls spielen, manchmal gewinnen, manchmal verlieren. Im Allgemeinen erwecken sie den Anschein von Fair Play. Eine beliebige Person, die bei diesem Spiel eine Wette abschließt, bekommt ihr Geld nicht zurück, selbst wenn sie richtig liegt. Egal, ob es sich um 3 Karten oder 3 Gläser und einen Ball handelt, sobald ein Spieler eine Karte aufdeckt oder ein Glas hebt, beugen sich diese Helfer angeblich vor, um genauer hinzuschauen, und versperren so die Sicht von zufälligen Zeugen. Wenn der Spieler es erraten hat, kann er es einfach anfechten und sagen: Nein, das hast du nicht. Wenn ein "Trottel" sehr entrüstet ist, kann er ihm sogar in den Nacken treten. Der "Katala" selbst muss sich nicht einmal anstrengen, um den Spieler zu verwirren, seine Aufgabe ist es, den Einsatz zu erhalten.

Haben Sie persönlich schon einmal erlebt, dass ein Spieler einen Tipp abgegeben hat, ihm aber der Gewinn nicht ausgezahlt wurde? Ich habe noch nie jemanden gewinnen sehen, außer ihren Komplizen.

Diese drei Karten oder drei Fingerhüte sind nach der Wahrscheinlichkeitstheorie für die Organisatoren des Spiels gewinnbar, und dann ist da noch der Taschenspielertrick.

 
hartmann:
Es ist wie mit dem Radio, das angeblich von Popov erfunden wurde.

ein normales Martingal...

Aber was für ein schickes MO, unendlich zu gewinnen!

 
Novaja:

Aber was für ein großartiges MO, das die Unendlichkeit gewinnt!

Hier, ich habe die Rechnung gemacht.
für 100.000 Spiele beträgt die Zahl 8,32 Rubel.
für eine Million Spiele eine Zahl von 25,76 Rubel.

Je mehr Spiele, desto höher die Zahl.
Es ist wie beim Martingal: Je mehr man spielt, desto wahrscheinlicher ist es, dass man verliert.
Dateien:
5mro81.zip  3420 kb
 

Die Bedingungen des Spiels sind wie üblich nicht vollständig beschrieben.

Ist es möglich, mehr zu gewinnen als Sie gesetzt haben? Wenn nicht, hat es keinen Sinn zu spielen.

Dann sollte sie aus dem Topf gewinnen dürfen. Es reicht also, den Mindesteinsatz zu machen, und schon gibt es einen Gewinn.

Vielleicht ist die Bedingung, dass man 1 Mal spielen kann, und hier müssen wir uns für den Einsatz entscheiden, so dass die maximale Gewinnwahrscheinlichkeit gegeben ist.

Wie alle "Pradlocks" - aus unvollständigen Bedingungen.

Lösung:

Es geht nicht einmal um Wetten. Einsatz 1. Mehr macht keinen Sinn, denn die Gewinnwahrscheinlichkeit hängt nicht von der Höhe des Einsatzes ab. Also 1, nur um das Spiel zu beginnen.

Worin besteht also das Paradoxon? Ausgehend von der Annahme, dass Sie einen größeren Einsatz tätigen müssen, um Ihren Gewinn zu erhöhen? Das könnte es sein.

 
Novaja:

Aber was für ein großartiges MO, das die Unendlichkeit gewinnt!

dies ist eine nicht-lineare Funktion.
y=2^x.


und wohin tendiert Y bei einer nichtlinearen Funktion, wenn X gegen unendlich tendiert? genau, ins unendliche.



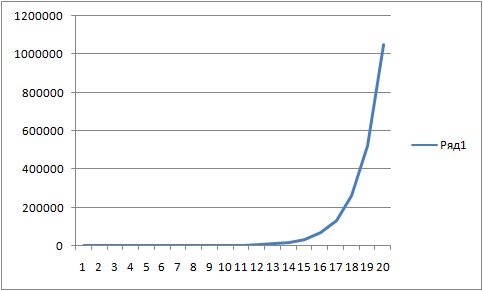
Wenn also die Anzahl der Spiele = unendlich ist, dann ist der durchschnittliche Gewinn = unendlich.

Und das Problem ist auch so gestellt, dass seine Verluste eine lineare Funktion sind (immer 25 Rubel pro Stück), während seine Gewinne eine nichtlineare Funktion sind.

Die erste Kurve wird höher sein als die zweite, dann werden die Plätze getauscht.

Das hängt von der Anzahl der Spiele ab.
123456789...25
Neuer Kommentar