MetaTrader 5 / Handelssysteme
English Русский 中文 Español 日本語 Português
Money Management von Vince. Implementierung als Modul für MQL5 Wizard

Money Management von Vince. Implementierung als Modul für MQL5 Wizard

MetaTrader 5 — Handelssysteme | 10 April 2018, 10:58
1 182 0
Dmitrii Troshin
Dmitrii Troshin

Einführung

Während wir an den Finanzmärkten arbeiten, sind wir ständig auf der Suche nach einem System, das uns hilft, Gewinne zu erzielen. Natürlich wollen wir, dass dieses System stabil ist und das Risiko minimiert wird. Um eine solche Strategie zu finden, werden verschiedene Handelssysteme entwickelt, die nach optimalen Ein- und Ausgängen suchen. Solche Systeme beinhalten technische Indikatoren und Handelssignale, die Auskunft darüber geben, wann man kaufen und verkaufen sollte. Es gibt ein ganzes System von Preismustern für die technische Analyse. Gleichzeitig zeigt Ralph Vince in seinem Buch "Mathematics of Money Management" , dass die Höhe des eingesetzten Kapitals für die Durchführung von Geschäften nicht weniger wichtig ist. Um den Gewinn zu optimieren und eine Einlage zu sparen, ist es notwendig, die Losgröße (lot size) für den Handel zu bestimmen.

Außerdem widerlegt Vince populäre "falsche Konzepte". Eines dieser Konzepte lautet zum Beispiel: "Je höher das Risiko, desto höher der Gewinn":

Der potenzielle Gewinn ist eine lineare Funktion des potenziellen Risikos. Das ist nicht wahr!

Das nächste "falsche Konzept" ist "Diversifikation reduziert Verluste". Auch das ist falsch. Vince schreibt:

 Diversifizierung kann Verluste reduzieren, aber nur bis zu einem gewissen Grad, viel weniger als die meisten Händler glauben.


Grundlagen

Zur Verdeutlichung werden die Grundgedanken anhand von Beispielen erläutert. Angenommen, wir haben ein bedingtes System von zwei Geschäften. Der erste Handel gewinnt 50% und der zweite verliert 40%. Wenn wir den Gewinn nicht reinvestieren, verdienen wir 10%. Wenn wir es reinvestieren, würde die gleiche Reihenfolge von Geschäften zu 10% des Verlustes führen. (GuV=Gewinn oder Verlust).

Positionsnummer GuV ohne Wiederanlage Gesamtkapital
GuV mit Wiederanlage Gesamtkapital


100

100
1 +50 150
+50 150
2 -40 110
-60 90

Die Reinvestition des Gewinns machte das Gewinnsystem zu einem Verlierer. Dabei spielt die Reihenfolge der Geschäfte keine Rolle. Das Beispiel zeigt, dass sich die Strategie bei der Wiederanlage vom Handel mit einem festen Lot unterscheiden muss. Die Suche nach einer optimalen Losgröße bei der Reinvestition ist also die Grundlage von Vince' Money Management Methode.

Fangen wir mit dem Einfachen an und kommen dann zum Komplexen. Beginnen wir mit dem Münzwurf. Angenommen, wir bekommen 2 Dollar im Falle eines Gewinns und verlieren 1 Dollar im Falle eines Verlustes. Die Wahrscheinlichkeit zu verlieren oder zu gewinnen ist 1/2. Angenommen, wir haben 100 Dollar. Wenn wir dann 100 Dollar setzen, wäre unser potenzieller Gewinn 200 Dollar. Aber im Falle eines Verlustes würden wir alles Geld verlieren und könnten das Spiel nicht fortsetzen. Während eines unendlichen Spiels, das das Ziel der Optimierung ist, würden wir definitiv verlieren.

Wenn wir nicht alles Geld auf einmal setzen und einen Teil davon verwenden würden, zum Beispiel 20 Dollar, hätten wir das Geld, um das Spiel fortzusetzen. Betrachten wir die Reihenfolge der möglichen Geschäfte mit einem anderen Kapitalanteil pro Handel. Das Anfangskapital beträgt 100 Dollar.

Positionen G&V wenn K=0.1 Capital    G&V wenn K=0.2 Capital     G&V wenn K=0.5  Capital    G&V wenn K=0.7 Capital     G&V wenn K=1 Capital  
    100         100         100         100         100
+2 20 120    40 140    100 200    140 240    200 300 
-1 -12 108    -28 112    -100  100   -168 72    -300 0 
+2 21.6 129.6    44.8 156.8    100 200    100.8 172.8    0 0 
-1 -12.96 116.64    -31.36 125.44    -100 100    -120.96 51.84    0 0 
+2 23.33 139.97    50.18 175.62    100 200    72.58 124.42    0 0 
-1 -14 125.97   -35.12 140.5   -100 100   -87.09 37.32   0 0
Total     126      141      100      37      0

Wie oben erwähnt, hängt der Gewinn/Verlust nicht von der Reihenfolge der Geschäfte ab. So ist der Wechsel von profitablem und verlustreichem Handel richtig. 

Es muss einen optimalen Koeffizienten (Divisor) geben, bei dem der Gewinn maximal ist. Für einfache Fälle, in denen die Gewinnwahrscheinlichkeit und das Verhältnis von Gewinn und Verlust konstant sind, kann dieser Koeffizient nach Kellys Formel ermittelt werden:

f=((B+1)*P-1)/B

f ist die optimale Konstante, die wir suchen.

P ist die Gewinnwahrscheinlichkeit

B ist das Gewinn/Verlust-Verhältnis

Zur Vereinfachung nennen wir f einen Koeffizienten.

In der Praxis ändern sich Größe und Gewinnwahrscheinlichkeit ständig, so dass Kellys Formel nicht anwendbar ist. Daher wird der Koeffizient f für empirische Daten durch numerische Methoden ermittelt. Die Rentabilität des Systems wird für einen beliebigen empirischen Handelsfluss optimiert. Für einen Handelsgewinn verwendet Vince den Begriff HPR (Holding Period Returns oder Haltedauer-Rendite). Wenn eine Position einen Gewinn von 10% erzielt hat, dann ist HPR =1+0.1=1.1. Also, die Berechnung je Position ist: HPR =1+f*Ergebnis/(Maximal möglicher Verlust), wobei Renditen das Vorzeichen von plus oder minus haben können, je nachdem ob es sich um Gewinn oder Verlust handelt. Tatsächlich ist f der Koeffizient der maximal möglichen Absenkung (drawdown). Um einen optimalen f Wert zu finden, müssen wir das Maximum des Produktes aller Positionen max(HPR1 * HPR2 * .... *HPRn) ermitteln.

Schreiben wir ein Programm, um f für ein beliebiges Datenarray auszufüllen.

Programm 1. Ermitteln des optimalen f.

double PL[]={9,18,7,1,10,-5,-3,-17,-7};  // Ein Array für Gewinn/Verlust aus den Büchern
double Arr[]={2,-1};

void OnStart()
{
SearchMaxFactor(Arr);                   //Oder PL und ein anderer Array

}

void SearchMaxFactor(double &arr[])
{
double MaxProfit=0,K=0;                  // Maximalgewinn
                                         // und das Verhältnis gemäß des Gewinns
for(int i=1;i<=100;i++)
{
   double k,profit,min;
   min =MathAbs(arr[ArrayMinimum(arr)]); // Ermitteln des Maximalverlustes im Array
   k =i*0.01;                            
   profit =1;
// Rückgabe des Gefundenen mit den Koeffizienten
      for(int j=0;j<ArraySize(arr);j++)
      {
         profit =profit*(1+k*arr[j]/min);
      }
// Vergleich mit dem Maximalgewinn 
   if(profit>MaxProfit)
   {
   MaxProfit =profit;
   K=k;
   }
}
Print("Optimal K  ",K," Profit   ",NormalizeDouble(MaxProfit,2));

}

Wir können prüfen, dass für den Fall +2,-1,+2,-1, usw. f gleich dem Ergebnis der Kelly-Formel ist.

Beachten Sie, dass eine Optimierung nur für profitable Systeme sinnvoll ist, d.h. Systeme mit der positiven, mathematischen Erwartung (durchschnittlicher Gewinn). Für Verlustsysteme ist optimal f=0. Auch eine Größenbestimmung des Volumens kann aus einem Verlustsystem keinen Gewinner machen. Umgekehrt, wenn es im Handelsverlauf keine Verluste, d.h. wenn alle GuV>0, macht die Optimierung auch keinen Sinn: f= 1, und wir sollten das maximale Los handeln.

Mit den grafischen Möglichkeiten von MQL5 können wir den maximalen Wert von f finden und die gesamte Kurve der Gewinnverteilung in Abhängigkeit von f betrachten. Das folgende Programm zeichnet die Gewinnkurve in Abhängigkeit des Koeffizienten f.

Programm 2. Grafik des Gewinns in Abhängigkeit von f.

//+------------------------------------------------------------------+
//|                                                      Graphic.mq5 |
//|                                                       Orangetree |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Orangetree"
#property link      "https://www.mql5.com"
#property version   "1.00"

#include<Graphics\Graphic.mqh>
//+------------------------------------------------------------------+
//| Script Programm Start Funktion                                   |
//+------------------------------------------------------------------+
//double PL[]={9,18,7,1,10,-5,-3,-17,-7};             // Ein Array für Gewinn/Verlust aus den Büchern
double PL[]={2,-1};

void OnStart()
  {
double X[100]={0};
for(int i=1;i<=100;i++)
   X[i-1]=i*0.01;
double Y[100];
                                      
double min =PL[ArrayMinimum(PL)];                   

if(min>=0){Comment("f=1");return;}
min =MathAbs(min);

int n = ArraySize(X);
double maxX[1]= {0};
double maxY[1] ={0};

for(int j=0;j<n;j++)
{
   double k =X[j];
   double profit =1;
   for(int i=0;i<ArraySize(PL);i++)
   {
     profit =profit*(1+k*PL[i]/min);
   }
   Y[j] =profit;
   if(maxY[0]<profit)
   {
      maxY[0] =profit;
      maxX[0] =k;
   }
}  
CGraphic Graphic;
Graphic.Create(0,"Graphic",0,30,30,630,330);
CCurve *Curve=Graphic.CurveAdd(X,Y,ColorToARGB(clrBlue,255),CURVE_LINES,"Profit");
Curve.LinesStyle(STYLE_DOT);

//Falls gewünscht, kann der Graph geglättet werden
/*Curve.LinesSmooth(true);
Curve.LinesSmoothTension(0.8);
Curve.LinesSmoothStep(0.2);*/




CCurve *MAX =Graphic.CurveAdd(maxX,maxY,ColorToARGB(clrBlue,255),CURVE_POINTS,"Maximum");
MAX.PointsSize(8);
MAX.PointsFill(true);
MAX.PointsColor(ColorToARGB(clrRed,255));
Graphic.XAxis().MaxLabels(100);
Graphic.TextAdd(30,30,"Text",255);  
Graphic.CurvePlotAll();
Graphic.Update(); 
Print("Max factor f =   ", maxX[0]);  
  }


Der Graph für {+2,-1} schaut so aus:

Gewinn


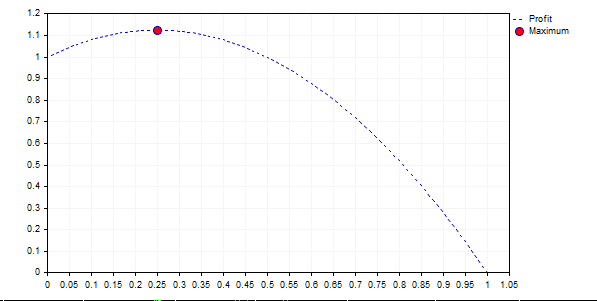
Die Grafik zeigt, dass folgende Regel falsch ist: "Je höher das Risiko, desto höher der Gewinn". In allen Fällen, in denen die Kurve unter 1 (f> 0.5) liegt, haben wir schließlich einen Verlust, und bei einem unendlichen langen Spiel schließlich eine 0 auf dem Konto.

Hier gibt es einen interessanten Widerspruch. Je höher die mathematische Gewinnerwartung und je stabiler das System, desto größer ist f. Zum Beispiel sei die Ergebnisreihe {-1,1,1,1,1,1,1,1,1,1,1,1}, der Koeffizient wird gleich 0,8. Sieht aus wie ein traumhaftes System. Aber ein Koeffizient von 0.8 bedeutet, dass der maximal zulässige Verlust 80% beträgt und Sie einmal 80% Ihres Kontos verlieren können! Aus Sicht der mathematischen Statistik ist dies die optimale Losgröße für die Maximierung der Bilanz, aber sind Sie bereit für solche Verluste?


Ein paar Worte zur Diversifikation

Angenommen, wir haben zwei Handelsstrategien: A und B, mit der gleichen Verteilung von Gewinn und Verlust, zum Beispiel (+2,-1). Das optimales f ist gleich 0,25. Betrachten wir die Fälle, in denen die Systeme eine Korrelation von 1,0 und -1 haben. Der Kontostand wird zu gleichen Teilen auf beide Systeme aufgeteilt.

Korrelation 1, f=0,25

System A Handel G&V   System B Handel G&V   Kombiniertes Konto
   50      50    100
2 25   2 25   150
-1 -18.75   -1 -18.75   112.5
2 28.13   2 28.13   168.75
-1 -21.09   -1 -21.09   126.56
             Profit 26.56

Diese Variante unterscheidet sich nicht vom Handel mit einer Strategie über das gesamte Kapital. Nun sehen wir die Korrelation gleich 0.

Korrelation 0, f=0,25

System A Handel G&V System B Handel G&V Kombiniertes Konto
   50    50  100
2 25 2 25 150
2 37.5 -1 -18.75 168.75
-1 -21.1 2 42.19 189.85
-1 -23.73 -1 -23.73 142.39




Profit 42.39

Der Gewinn ist jetzt viel höher. Und die Korrelation ist am Ende -1.

Korrelation -1, f=0.25

System A Handel G&V System B Handel G&V Kombiniertes Konto
   50    50  100
2 25 -1 -12.5 112.5
-1 -14.08 2 28.12 126.56
2 31.64 -1 -15 142.38
-1 17.8 2 35.59 160.18




Profit 60.18

In diesem Fall ist der Gewinn am höchsten. Diese und ähnliche Beispiele zeigen, dass die Reinvestitionsdiversifikation bei Gewinnen zu besseren Ergebnissen führt. Aber es ist auch klar, dass es nicht den schlimmsten Fall (in unserem Fall den größten Verlust f=0.25 des Saldos) eliminiert, mit Ausnahme der Variante, wenn die Korrelation der Systeme -1 ist. In der Praxis gibt es keine Systeme mit der Korrelation von genau -1. Dies ist analog zur Eröffnung von Positionen des gleichen Symbols in verschiedene Richtungen. Basierend auf solchen Argumenten kommt Vince zu folgendem Schluss. Hier ist ein Zitat aus seinem Buch:

Diversifikation, wenn sie richtig durchgeführt wird, ist eine Technik, die die Rendite erhöht. Sie reduziert nicht notwendigerweise die Inanspruchnahme (drawdown) im schlimmsten Fall. Das steht im krassen Widerspruch zu der weit verbreiteten Vorstellung.


Korrelation und andere Statistiken

Bevor wir zu den parametrischen Methoden zum Ermitteln von f kommen, lassen Sie uns noch einige Eigenschaften der Folge von Gewinn und Verlust betrachten. Wir können eine Reihe von zusammenhängenden Ergebnissen erzielen. Auf gewinnbringende Positionen folgen gewinnbringende Positionen, und auf verlorene Positionen folgen verlorene Positionen. Um solche Abhängigkeiten zu identifizieren, betrachten wir die folgenden zwei Methoden: die Autokorrelation einer Serie und einen seriellen Test Autokorrelation).

Ein serieller Test ist die Berechnung eines Wertes, der "Z-Wert" (z-score) genannt wird. Inhaltlich besagt der Z-Wert, um wie viel die Standardabweichungen der Daten vom Mittelwert der Normalverteilung abweichen. Ein negativer Z-Wert zeigt an, dass es weniger Streifen (kontinuierliche Gewinn-/Verlustfolge) als in der Normalverteilung gibt, so dass dem Gewinn wahrscheinlich ein Verlust folgt und umgekehrt. Formel zur Berechnung des Z-Wertes:

Z=(N(R-0.5)-Х)/((Х(Х-N))/(N-1))^(1/2)

oder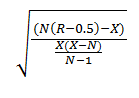Formel

wobei:

  • N ist die Gesamtzahl der Positionen
  • R ist die Gesamtzahl der Folgen
  • X=2*W*L, wobei
  • W = die Gesamtzahl der Gewinner der Folge
  • L = die Gesamtzahl der Verlierer der Folge

Program 3. Z Score.

double Z(double &arr[])
{
int n =ArraySize(arr);
int W,L,X,R=1;
   if(arr[0]>0)
   {
      W=1;
      L=0;
   }
   else
   {
      W=0;
      L=1;
   }

   for(int i=1;i<n;i++)
   {
    if(arr[i]>0)
      {
      W++;
      if(arr[i-1]<=0){R++;}
      }
    else
      {
      L++;
      if(arr[i-1]>0){R++;}
      }    
   }
 X =2*W*L;
 double x=(n*(R-0.5)-X);
 double y =X*(X-n);
 y=y/(n-1);
 double Z=(n*(R-0.5)-X)/pow(y,0.5);  
Print(Z);
return Z;
}

Der Z-Wert wird vom Strategy Tester berechnet, wo er im Backtest Report "Z-Score" genannt wird.

Die serielle Korrelation ist eine statische Beziehung zwischen einer Folge von Werten, die mit einer Verschiebung verwendet wird. Für die Serie {1,2,3,4,5,6,7,8,9,10} ist es eine Korrelation zwischen {1,2,3,4,5,6,7,8,9} und {2,3,4,5,6,7,8,9,10}. Nachfolgend finden Sie ein Programm, das die serielle Korrelation ermittelt.

Programm 4. Serielle Korrelation.

double AutoCorr(double &arr[])
{
   int n =ArraySize(arr);
   
   double avr0 =0;
   for(int i=0;i<n-1;i++)
   {
   avr0=avr0+arr[i];
   }
   avr0=avr0/(n-1);
   
   double avr1 =0;
   
   for(int i=1;i<n;i++)
   {
   avr1=avr1+arr[i];
   }
   avr1=avr1/(n-1);
   
   double D0 =0;
   double sum =0.0;
   
   for(int i=0;i<n-1;i++)
   {
   sum =sum+(arr[i]-avr0)*(arr[i]-avr0);
   }
   D0 =MathSqrt(sum);
   
   double D1 =0;
   sum =0.0;
   for(int i=1;i<n;i++)
   {
   sum =sum+(arr[i]-avr1)*(arr[i]-avr1);
   }
   D1 =MathSqrt(sum);
   
   sum =0.0;
   for(int i=0;i<n-1;i++)
   {
   sum =sum +(arr[i]-avr0)*(arr[i+1]-avr1);
   }
   if(D0==0||D1==0) return 1;
   double k=sum/(D0*D1);
return k;
}

Wenn die Ergebnisse von Trades miteinander verknüpft sind, kann die Handelsstrategie angepasst werden. Bessere Ergebnisse werden erzielt, wenn wir zwei verschiedene Koeffizienten f1 und f2 für Gewinne und Verluste verwenden. Für diesen Fall werden wir ein separates Money-Management-Modul in MQL5 schreiben.

Parametrische Methoden

Bei der Optimierung der Parameter des Systems können wir zwei Ansätze verwenden. Der erste Ansatz ist empirisch und basiert direkt auf den experimentellen Daten. In diesem Fall optimieren wir die Parameter für ein bestimmtes Ergebnis. Der zweite Ansatz ist parametrisch. Sie basiert auf funktionalen oder statischen Abhängigkeiten. Ein Beispiel für die parametrische Methode ist die Ermittlung des optimalen Koeffizienten aus der Kelly-Formel. 

Vince schlägt vor, die Verteilungen der erhaltenen Renditen zu verwenden, um den optimalen Koeffizienten zu finden. Zuerst betrachtet Vince die Normalverteilung, die best-untersuchte und die beliebteste ist. Dann konstruiert er eine generalisierte Verteilung.

Das Problem ist wie folgt formuliert. Angenommen, unsere Gewinne/Verluste werden nach der Normalverteilung (oder einer anderen) verteilt. Dann ermitteln wir das optimale f für diese Verteilung. Im Falle einer Normalverteilung können wir mit den experimentellen Daten arbeiten, um den Mittelwert und die Standardabweichung der Folge von PL zu berechnen. Diese beiden Parameter charakterisieren die Normalverteilung vollständig.

Hier ist die Formel der Dichte der Normalverteilung:

Dichte

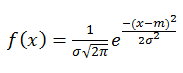
mit 

  • σ ist die  Standardabweichung
  • m it der mathematische Erwartungswert (Mittelwert).

Ich mochte die Idee. Die Art der Gewinn-/Verlustverteilung kann anhand empirischer Daten ermittelt werden. Dann können wir mit dieser Funktion bereits f- ermitteln und so den Einfluss von Zufallswerten zu vermeiden. Leider ist es in der Praxis nicht so einfach. Fangen wir mit dem Anfang an. Besprechen wir aber zuerst die Methode.

Verteilung

 

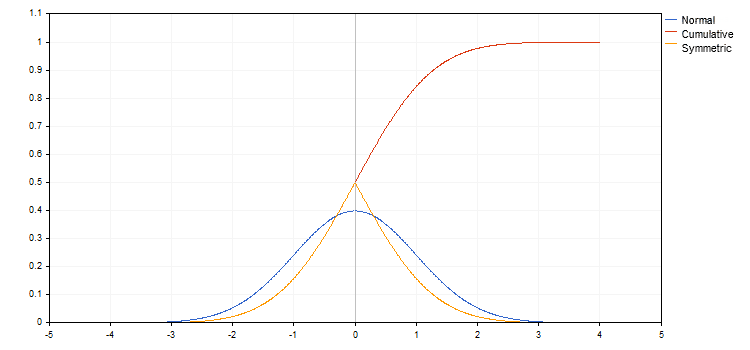
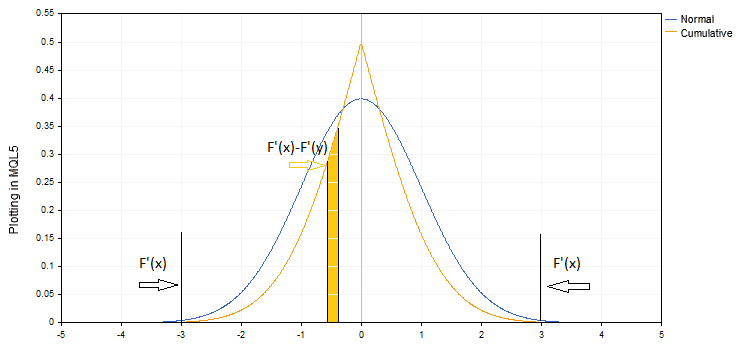
Der Graph der Dichte der Normalverteilung ist in diesem Diagramm blau dargestellt. Der Mittelwert ist gleich Null und die Standardabweichung gleich Eins. Die rote Farbe zeigt das Integral dieser Funktion. Dies ist eine kumulative Wahrscheinlichkeit, d.h. die Wahrscheinlichkeit, dass der Wert kleiner als oder gleich dem angegebenen X ist. Gewöhnlich bezeichnet mit F(x). Das orange Diagramm zeigt die Wahrscheinlichkeit, dass der Wert kleiner oder gleich x für x<0 ist, und dass der Wert größer oder gleich x für x>0 ist (F(x)' =1-F(x), für x>0. Alle diese Funktionen sind bekannt und ihre Werte sind einfach zu erhalten.

Wir müssen das größte geometrische Mittel der nach diesem Gesetz verteilten Positionen finden. Hier schlägt Vince die folgenden Aktionen vor.

Zuerst finden wir die Eigenschaften der Verteilung, d.h. den Mittelwert und die Standardabweichung. Dann wählen wir das "Konfidenzintervall" oder die Schnittbreite, die in Standardabweichungen ausgedrückt wird. In der Regel wird das Intervall 3σ gewählt. Werte größer als 3σ werden abgeschnitten. Danach wird das Intervall in Segmente geteilt und dann werden die zugehörigen Werte der Gewinne/Verluste (PL) gefunden. Zum Beispiel für σ=1 und m=0 ist der Wert der zugehörigen PL an den Grenzen des Intervalls m +- 3σ = +3 und -3. Wenn wir das ganze Intervall in kleinere der Breite 0.1σ aufteilen, dann sind die zugehörigen PL -3, -2.9, -2.8 .... 0... 2.8, 2,9, 3. Für diese Folge von PL finden wir das optimale f.

Da verschiedene Werte von PL eine unterschiedliche Wahrscheinlichkeit haben, wird für jeden Wert eine individuelle "assoziierte Wahrscheinlichkeit" P gefunden. Danach wird das Maximum der Produkte ermittelt:

HPR=(1+PL*f/maxLoss)^P, wobei maxLoss der maximale Verlust (modulo) ist.

Vince schlägt vor, die kumulative Wahrscheinlichkeit als zugehörige Wahrscheinlichkeit zu verwenden. Die kumulative Wahrscheinlichkeit F'(x) ist in unserer Grafik orange dargestellt.

Logischerweise sollte die kumulative Wahrscheinlichkeit nur für Extremwerte genommen werden, für die anderen Werte hingegen P=F'(x)-F'(y), wobei x und y Werte von F(x) an den Grenzen des Intervalls.

Wahrscheinlichkeiten

 

Dann wäre HPR=(1+PL*f/maxLoss)^P eine Art wahrscheinlichkeitsgewichteter Wert. Wie erwartet, wäre die Gesamtwahrscheinlichkeit dieser Werte gleich 1. Vince räumt in seinem Buch ein, dass die auf diese Weise erzielten Ergebnisse nicht mit den Ergebnissen der tatsächlichen Daten übereinstimmen. Er bindet ein solches Ergebnis an die begrenzte Art der Probenahme und die Differenz zwischen der tatsächlichen und der normalen Verteilung. Es wird angenommen, dass bei einer erhöhten Anzahl von Elementen und deren Verteilung nach der Normalverteilung die parametrischen und tatsächlichen Werte des optimalen fKoeffizienten übereinstimmen würden.

In dem nach Vince's Methode analysierten Beispiel ist die Gesamtwahrscheinlichkeit gleich 7,9. Vince findet den geometrischen Mittelwert, indem er einfach die Wurzel des Ergebnisses von 7,9ten Grad nimmt. Anscheinend muss es eine strenge mathematische Rechtfertigung für einen solchen Ansatz geben.

Mit dem MQL5-Tool können wir das leicht überprüfen. Zu diesem Zweck verwenden wir die Bibliothek Normal.mqh, die sich unter <Math\Stat\Normal.mqh> befindet.

Ich habe zwei Versionen zum Experimentieren erstellt: eine nach Vince und die andere, wie oben beschrieben. Die Bibliotheksfunktion MathCumulativeDistributionNormal(PL,mean,stand,ProbCum) wird verwendet, um zugehörige Wahrscheinlichkeiten zu finden.

 Programm 5. Finden des optimalen f in der Normalverteilung (nach Vince). 

//+------------------------------------------------------------------+
//|                                                        Vince.mq5 |
//|                        Copyright 2017, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

#include<Math\Stat\Math.mqh>
#include<Math\Stat\Normal.mqh>

input double N=3;                      // Cut-Off-Intervall der Standardabweichung
input int M=60;                        // Anzahl der Segmente
//+------------------------------------------------------------------+
//| Script Programm Start Funktion                                   |
//+------------------------------------------------------------------+
void OnStart()
  {
double arr[10000];  
bool ch =MathRandomNormal(1,8,10000,arr);
double mean =MathMean(arr);
double stand =MathStandardDeviation(arr);

double PL[];                      // Array der "zugehörigen Gewinne"
ArrayResize(PL,M+1);
                                  // Ausfüllen des Arrays
for(int i=0;i<M+1;i++)
   {
   double nn =-N+2.0*i*N/M;
   PL[i] =stand*nn+mean;
   }
//............................. An array of "associated probabilities"
double ProbCum[];
ArrayResize(ProbCum,M+1);
//............................. Filling the array..................
ch =MathCumulativeDistributionNormal(PL,mean,stand,ProbCum);
//F'(x)= 1-F(x) wenn х>0

for(int i=0,j=0;i<M+1;i++)
{
if(i<=M/2)continue;
else j=M-i;
ProbCum[i] =ProbCum[j];
}

double SumProb=0;
for(int i=0;i<M+1;i++)
{
SumProb =SumProb+ProbCum[i];
}
Print("SumProb ",SumProb);
double MinPL =PL[ArrayMinimum(PL)];
double min =arr[ArrayMinimum(arr)];

double f=0.01,HPR=1,profit=1; 
double MaxProfit=1,MaxF=0;


for(int k=0;k<1000;k++)
   {
   f=k*0.001;
   profit =1;  
      for(int i=0;i<M+1;i++)
      {
      HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]);
      profit =HPR*profit;
      }
   if(MaxProfit<profit)
     {
     MaxF =f;
     MaxProfit =profit;
     } 
   }
Print("Profit Vince");   
Print(MaxF,"   ",pow(MaxProfit,1/SumProb),"  ",Profit(MaxF,min,arr));
//... Zum Vergleich finden wir den Maximalgewinn mit den aktuellen Daten
MaxF =0;
MaxProfit =1;

for(int k=0;k<1000;k++)
   {
   f=k*0.001;
   profit =Profit(f,min,arr);  

   if(MaxProfit<profit)
     {
     MaxF =f;
     MaxProfit =profit;
     } 
   }
Print("------MaxProfit-------");   
Print(MaxF,"   ",MaxProfit);

  }

//   Ein Programm zum Ermitteln des Gewinns mit den aktuellen Daten 
//   aus arr[], dem Array mit dem Minimum 'min'
//   und des angegebenen Wertes für f

double Profit(double f,double min, double &arr[])
{
if(min>=0)
{
   return 1.0;
   Alert("min>=0");
}

double profit =1;
int n =ArraySize(arr);
   for(int i=0;i<n;i++)
   {
   profit =profit*(1-arr[i]*f/min);
   }
return profit;
}

Der Programmcode ist in der Datei Vince.mq5 verfügbar.

Dieses Programm hat einen Koeffizienten aus einer Normalverteilung und dann aus aktuellen Daten. Die zweite Variante unterscheidet sich nur in einer Reihe von "assoziierten" Wahrscheinlichkeiten und PL.

Programm 6. 

.............................................
double ProbDiff[];
ArrayResize(ProbDiff,M+2);
double PLMean[];
ArrayResize(PLMean,M+2);

ProbDiff[0]=ProbCum[0];
ProbDiff[M+1]=ProbCum[M];
PLMean[0]=PL[0];
PLMean[M+1]=PL[M];

for(int i=1;i<M+1;i++)
{
ProbDiff[i] =MathAbs(ProbCum[i]-ProbCum[i-1]);
PLMean[i] =(PL[i]+PL[i-1])/2;
}
..............................................

Der Programmcode ist in der Datei Vince_2.mq5 enthalten.

Hier PLMean[i] =(PL[i]+PL[i-1>1])/2; ist der Durchschnittswert von PL im Intervall, ProbDiff[] ist die Wahrscheinlichkeit des gegebenen Intervalls. Werte an den Grenzen werden abgeschnitten (eventuell durch Stop-Loss oder Take-Profit), so dass die Wahrscheinlichkeit an den Grenzen gleich der kumulativen Wahrscheinlichkeit ist.

Diese beiden Programme arbeiten ungefähr auf die gleiche Weise und liefern ungefähr die gleichen Ergebnisse. Es stellte sich heraus, dass die Reaktion stark von der Schnittbreite N (dem so genannten Konfidenzintervall) abhängt. Die enttäuschendste Tatsache ist, dass, wenn N steigt, der f-Koeffizient, der sich aus der Normalverteilung ergibt, auf 1 tendiert. Theoretisch sollte das Ergebnis umso genauer sein, je größer das Konfidenzintervall ist. In der Praxis geschieht dies jedoch nicht.

Dies kann durch einen kumulierten Fehler verursacht werden. Die Exponentialfunktion nimmt schnell ab, und wir müssen mit kleinen Werten arbeiten: HPR=pow((1-PL[i]/MinPL*f),ProbCum[i]). Die Methode selbst kann auch einen Fehler enthalten. Aber es ist für den praktischen Gebrauch vernachlässigbar. In jedem Fall müssen wir den Parameter N "anpassen", was das Ergebnis stark beeinflusst.

Natürlich unterscheidet sich jede Folge von PL von der Normalverteilung. Deshalb erstellt Vince eine verallgemeinerte Verteilung mit den Parametern, die die Eigenschaften einer beliebigen Zufallsverteilung emulieren. Parameter, die verschiedene Momente der Verteilung (Mittelwert, Kurtosis, Breite, Schiefe) einstellen, werden hinzugefügt. Dann werden numerische Methoden verwendet, um diese Parameter für empirische Daten zu finden, und es wird eine Funktion für Folge der PL-Verteilung erstellt.

Da mir die Ergebnisse von Experimenten mit Normalverteilung nicht gefielen, entschied ich mich, keine numerischen Berechnungen mit der generalisierten Verteilung durchzuführen. Hier ist ein weiteres Argument, das meine Zweifel erklärt. 

Vince behauptet, dass parametrische Methoden viel leistungsfähiger sind. Mit zunehmender Anzahl der Experimente werden die Daten zu theoretischen Ergebnissen tendieren, da der aus der Probe gewonnene Koeffizient aufgrund der begrenzten Probenahme ungenau ist. Die Parameter für die Normalverteilung (Mittelwert und Standardabweichung) werden jedoch aus der gleichen begrenzten Stichprobe gewonnen. Die Ungenauigkeit bei der Berechnung der Verteilungseigenschaften ist genau die gleiche. Die Ungenauigkeit nimmt aufgrund des aufgelaufenen Fehlers in weiteren Berechnungen weiter zu. Und dann stellt sich heraus, dass das Ergebnis in der praktischen Umsetzung auch von der Schnittbreite abhängt. Da die Verteilung in der Praxis nicht normal ist, fügen wir ein weiteres Element hinzu - die Suche nach der Verteilungsfunktion, die ebenfalls auf den gleichen empirischen Enddaten basiert. Das zusätzliche Element führt zu einem zusätzlichen Fehler.

Hier ist meine bescheidene Meinung. Der parametrische Ansatz zeigt, dass die Ideen, die in der Theorie gut aussehen, in der Praxis nicht immer so gut funktionieren.

Überblick über Vince' Buch

Hier ist eine kurze Zusammenfassung von Vince' "The Mathematics of Money Management". Das Buch ist eine Mischung aus einem Überblick über statistische Methoden mit verschiedenen Methoden, das optimale f zu finden. Es deckt ein breites Themenspektrum ab: das Markovitz-Portfoliomanagement-Modell, den Kolmogorov-Smirnov-Test für Ausschüttungen, das Black-Sholes-Aktienoptionspreismodell und sogar Methoden zur Lösung von Gleichungssystemen. Diese breite Abdeckung geht weit über den Rahmen eines einzelnen Artikels hinaus. Und alle diese Methoden werden im Zusammenhang mit der Ermittlung des optimalen f betrachtet. Deshalb werde ich auf diese Methoden nicht näher eingehen, sondern zur praktischen Umsetzung übergehen. Die Methoden werden als Module für den MQL5 Wizard implementiert.


Das MQL5 Wizard Modul

Die Implementierung des Moduls ähnelt dem verfügbaren Standardmodul MoneyFixedRisk, bei dem die Losgröße auf Basis eines konfigurierten Stop-Loss-Wertes berechnet wird. Zu Demonstrationszwecken lassen wir den Stop-Loss unabhängig und setzen explizit f und den maximalen Verlust in den Eingangsparameter. 

Zuerst erstellen wir einen neuen Ordner für unsere Module im Include/Expert Verzeichnis - z.B. MyMoney. Dann erstellen wir die Datei MoneyF1.mql in diesem Ordner.

Alle Handelsmodule bestehen aus einem Satz von Standardteilen: der Handelsmodulklasse und ihrer speziellen Beschreibung. 

Die Klasse enthält in der Regel die folgenden Elemente:

  • Konstruktor
  • Destruktor
  • Eingabeparameter der Funktionen
  • Die Funktion ValidationSettings(void) zur Validierung der Parameter
  • Methoden zur Ermittlung des Positionsvolumens CheckOpenLong(double price, double sl) und CheckOpenShort(double price, double sl)

Nennen wir diese Klasse CMoneyFactor

class CMoneyFactor : public CExpertMoney
  {
protected:
   //--- Eingabeparameter
   double            m_factor;          // Maximalverlust-Koeffizient f
   double            m_max_loss;        // Maximalverlust in Punkten

public:
                     CMoneyFactor(void);
                    ~CMoneyFactor(void);
   //---
   void              Factor(double f)       { m_factor=f;}       
   void              MaxLoss(double point)  { m_max_loss=point;}         
   virtual bool      ValidationSettings(void);
   //---
   virtual double    CheckOpenLong(double price,double sl);               
   virtual double    CheckOpenShort(double price,double sl);
  };
//+------------------------------------------------------------------+
//| Konstruktor                                                      |
//+------------------------------------------------------------------+
void CMoneyFactor::CMoneyFactor(void) : m_factor(0.1),
                                        m_max_loss(100)
  {
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
void CMoneyFactor::~CMoneyFactor(void)
  {
  }

Der maximale Verlust in Punkten wird als Typ double für Standardmodule festgelegt. In anderen Standardmodulen, die im Standardpaket verfügbar sind, werden Stop-Loss und Take-Profit in Punkten festgelegt, die in der Basisklasse ExpertBase.mqh definiert sind.

   ExpertBase.mqh
   int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
   m_adjusted_point=m_symbol.Point()*digits_adjust;

Es bedeutet, dass ein Punkt gleich 10*Point() für Anführungszeichen mit 3 und 5 Nachkommastellen ist. 105 Punkte für Point() entsprechen 10.5 in Standard MQL5 Modulen.

Die Funktion Factor(double f) und MaxLoss(double point) setzen Eingabeparameter und sollten auf die gleiche Weise benannt werden, wie sie im Modul deskriptor beschrieben werden.

Die Funktion zur Validierung von Eingabeparametern:

bool CMoneyFactor::ValidationSettings(void)
  {
   if(!CExpertMoney::ValidationSettings())
   return(false);
//--- Anfangsprüfung der Daten  
   if(m_factor<0||m_factor>1)
   {
   Print(__FUNCTION__+"The coefficient value must be between 0 and 1");
   return false;   
   }
 
  return true;
  }

Prüfung, ob der Koeffizient zwischen 0 und 1 liegt.

Schließlich sind hier die Funktionen, die das Positionsvolumen bestimmen. Eröffnen einer Kaufposition:

double CMoneyFactor::CheckOpenLong(double price,double sl)
{
   if(m_symbol==NULL)
      return(0.0);
//--- Bestimmen von lot, der Losgröße
   double lot;
   
/*   
      ExpertBase.mqh
      int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
      m_adjusted_point=m_symbol.Point()*digits_adjust;
*/
    double loss;
    if(price==0.0)price =m_symbol.Ask();
    loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
    double stepvol=m_symbol.LotsStep();
    lot=MathFloor(m_account.Balance()*m_factor/loss/stepvol)*stepvol;
   
   double minvol=m_symbol.LotsMin();
//---Prüfen des Mindestlots
   if(lot<minvol)
      lot=minvol;
//---Prüfen des maximalen Lots
   double maxvol=m_symbol.LotsMax();
   if(lot>maxvol)
      lot=maxvol;
//--- Rückgabe des Handelsvolumens
   return(lot);

}

Hier wird die maximale Losgröße mit der Methode OrderProfitCheck() der Klasse CAccountInf aus der Bibliothek gefunden. Anschließend wird die Einhaltung der Grenzwerte für Minimal- und Maximalwerte überprüft.

Jedes Modul beginnt mit einem Deskriptor, den der Compiler benötigt, um das Modul zu erkennen.

// Wizard-Beschreibung, Anfang
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Trading with the optimal f coefficient                     |
//| Type=Money                                                       |
//| Name=FixedPart                                                   |
//| Class=CMoneyFactor                                               |
//| Page= ?                                                          |
//| Parameter=Factor,double,0.1,Optimum fixed share                  |
//| Parameter=MaxLoss,double,50,Maximum loss in points               |
//+------------------------------------------------------------------+
// wizard description end

Zu Testzwecken können Sie dieses Modul mit jedem vorhandenen Signalmodul kompilieren. Das ausgewählte Modul der Handelssignale kann auch mit einem Modul des Geldmanagements auf Basis eines festen Loses zusammengestellt werden. Die gewonnenen Ergebnisse werden verwendet, um den maximalen Verlust und die Folge der PL zu finden. Dann wenden wir Programm 1 auf diese Ergebnisse an, um das optimale f zu finden. So können die experimentellen Daten verwendet werden, um den optimale f zu ermitteln. Eine andere Möglichkeit ist, das optimale f direkt vom resultierenden Expert Advisor durch Optimierung zu finden. Ich hatte einen Unterschied in den Resultaten so wenig wie +/- 0.01. Diese Differenz ist auf Rechenfehler zurückzuführen, die mit Rundungen verbunden sein können.

Der Code des Moduls steht in der Datei MoneyF1.mqh zur Verfügung.

Die Folge unserer Gewinne/Verluste kann eine signifikante serielle Korrelation aufweisen. Dies kann mit den obigen Programmen zur Berechnung des Z-Scores und der seriellen Korrelation ermittelt werden. Dann können zwei Koeffizienten angegeben werden: f1 und f2. Der erste wird auf gewinnbringenden Positionen, der zweite auf Verlustpositionen angewendet. Schreiben wir das zweite Modul für das Geldmanagement für diese Strategie. Die Koeffizienten können dann über die Optimierung oder direkt aus den Ergebnisdaten der gleichen Strategie mit einem festen Los ermittelt werden.

Programm 7. Bestimmung der optimalen f1 und f2 auf Basis des Folge von PL.

void OptimumF1F2(double &arr[])
{
double f1,f2;
double profit=1;
double MaxProfit =0;
double MaxF1 =0,MaxF2 =0;
double min =MathAbs(arr[ArrayMinimum(arr)]);

   for(int i=1;i<=100;i++)
   {
   f1 =i*0.01;
      for(int j=1;j<=100;i++)
      {
         f2 =j*0.01;
         profit =profit*(1+f1*arr[0]/min);
            for(int n=1;n<ArraySize(arr);n++)
            {
            if(arr[n-1]>0){profit =profit*(1+f1*arr[n]/min);}
            else{profit =profit*(1+f2*arr[n]/min);}
            }
         if(MaxProfit<profit)
         {
         MaxProfit=profit;
         MaxF1 =i;MaxF2 =j;
         }   
      }
   }

Wir müssen auch die Grundfunktionen des Money Management Moduls für den MQL5 Wizard anpassen. Zuerst fügen wir einen weiteren f2-Parameter und eine Prüfung für diesen Parameter hinzu. Zweitens modifizieren wir die Funktionen CheckOpenLong() und CheckOpenShort(). Wir fügen auch CheckLoss() hinzu, um das Finanzergebnis der vorherigen Position zu ermitteln.

//+------------------------------------------------------------------+
//| Prüfen des Ergebnisses der vorherigen Position                   |
//+------------------------------------------------------------------+
double CMoneyTwoFact:: CheckLoss()
  {
double lot=0.0;
HistorySelect(0,TimeCurrent());

int deals=HistoryDealsTotal();           // Anzahl der Positionen in der Historie
CDealInfo deal;
//--- Suche nach der vorherigen Position
if(deals==1) return 1;
   for(int i=deals-1;i>=0;i--)
   {
   if(!deal.SelectByIndex(i))
      {
      printf(__FUNCTION__+": Failed to select a trade with the specified index");
      break;
      }
//--- Auswahl der Positionen auf Basis von Symbol und anderen Parameter
      if(deal.Symbol()!=m_symbol.Name()) continue;
//--- Rückgabe des Handelsergebnisses
    lot=deal.Profit();
    break;
   }

   return(lot);
  }

Die Funktionen CheckOpenLong() und CheckOpenShort():

double CMoneyTwoFact::CheckOpenLong(double price,double sl)
  {
   double lot=0.0;
   double p=CheckLoss();
   
/*   
      ExpertBase.mqh
      int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
      m_adjusted_point=m_symbol.Point()*digits_adjust;
*/
   
   double loss;
   
   if(price==0.0)price =m_symbol.Ask();   
   if(p>0)
      {
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol;
      }  
   if(p<0)
      { 
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_BUY,1.0,price,price - m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol;
      }


  return(lot);   
  }
//+------------------------------------------------------------------+

double CMoneyTwoFact::CheckOpenShort(double price,double sl)
  {
  double lot=0.0;
  double p=CheckLoss();
/*   int digits_adjust=(m_symbol.Digits()==3 || m_symbol.Digits()==5) ? 10 : 1;
   m_adjusted_point=m_symbol.Point()*digits_adjust;*/
   
   double loss;
   
   if(price==0.0)price =m_symbol.Ask();   
   if(p>0)
      {
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor1/loss/stepvol)*stepvol;
      }  
   if(p<0)
      { 
      loss=-m_account.OrderProfitCheck(m_symbol.Name(),ORDER_TYPE_SELL,1.0,price,price+m_max_loss*m_adjusted_point);
      double stepvol=m_symbol.LotsStep();
      lot=MathFloor(m_account.Balance()*m_factor2/loss/stepvol)*stepvol;
      }
  return(lot);     
  }

Der vollständige Code des Moduls ist in MoneyF1F2.mqh verfügbar.

Wie bereits erwähnt, ist Vince' Konzept des Money Managements grundsätzlich mit dem optimalen f verbunden. Daher reichen für das Beispiel zwei Module völlig aus. Sie können jedoch weitere Varianten implementieren. Beispielsweise können Sie Martingal-Elemente hinzufügen.


Anlagen

Die Datei Programs.mq5 enthält die im Artikel verwendeten Programmcodes. Ein Programm zum Lesen von Daten aus der Datei void ReadFile(string file,double &arr[]) ist ebenfalls unten angehängt. Das Programm ermöglicht das Finden von f basierend auf der Folge von PL aus dem Strategy Tester. Jemand möchte vielleicht eine ganze Klasse für das Parsen von Berichten schreiben, wie es im Artikel "Die Eröffnung durch Indikatoren bestimmen lassen" getan wird. Aber das wäre ein eigenes Programm mit eigenen Klassen.

Ich schlage einen einfacheren Weg vor. Führen Sie die Strategie mit einer festen Losgröße im Strategy Tester aus. Speichern Sie den Testerbericht als Open XML (MS Office Excel). Fügen Sie Swap und Provision zur Spalte Profit hinzu, um die Folge der PL zu erhalten. Speichern Sie diese Spalte in einer Text- oder CSV-Datei. So erhalten wir eine Reihe von Zeilen, die aus einzelnen Ergebnissen jedes Handels bestehen. Die Funktion ReadFile() liest diese Ergebnisse in das Array arr[] ein. So können wir den optimalen f basierend auf Daten jeder Strategie mit einem festen Los finden.

Die Dateien Vince.mq5 und Vince_2.mq5 enthalten den Quellcode der parametrischer Methoden, um das Optimum des Koeffizienten zu finden.

MoneyF1.mqh und MoneyF1F2.mqh enthalten den Quellcode der Money Management Module.

Die Dateien im angehängten Zip-Ordner sind in Übereinstimmung mit den MetaEditor-Verzeichnissen angeordnet.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/4162

Beigefügte Dateien |
ZIP herunterladen
Programs.mq5 (8.38 KB)
Vince.mq5 (5.91 KB)
Vince_2.mq5 (6.23 KB)
MoneyF1.mqh (9.63 KB)
MoneyF1F2.mqh (12.97 KB)
MQL5.zip (9.01 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Die Darstellung der Optimierung einer Handelsstrategie im MetaTrader 5 Die Darstellung der Optimierung einer Handelsstrategie im MetaTrader 5
Der Artikel implementiert eine MQL-Anwendung mit einem grafischen Interface zur erweiterten Darstellung der Optimierung. Das grafische Interface verwendet die letzte Version der Bibliothek EasyAndFast. Viele Anwender fragen sich, warum MQL-Anwendungen überhaupt grafische Interfaces benötigen. Dieser Artikel zeigt einen von mehreren Fällen, die für Händler nützlich sein können.
Multi-Symbol-Chart der Bilanz in MetaTrader 5 Multi-Symbol-Chart der Bilanz in MetaTrader 5
Der Artikel beschreibt ein Beispiel für eine MQL-Anwendung mit dem grafischen Interface, in welchem die Kurven der Bilanz und des Rückgangs für mehrere Symbole nach den Ergebnissen des letzten Tests angezeigt werden.
Wie erstellt man ein grafisches Panel beliebiger Komplexität? Wie erstellt man ein grafisches Panel beliebiger Komplexität?
Der Artikel beschreibt ausführlich, wie ein Panel auf der Basis der CAppDialog-Klasse erstellt wird und wie ihm Steuerelemente hinzufügt werden können. Sie liefert die Beschreibung der Panelstruktur und ein Schema, das die Vererbung von Objekten zeigt. Der Artikel zeigt auch, wie Ereignisse behandelt werden und wie sie an abhängige Steuerelemente übergeben werden. Weitere Beispiele zeigen, wie die Parameter des Panels wie Größe und Hintergrundfarbe bearbeitet werden können.
Wie man eine Anforderungsspezifikation bei der Bestellung eines Indikators erstellt Wie man eine Anforderungsspezifikation bei der Bestellung eines Indikators erstellt
Händler suchen nach Gesetzmäßigkeiten im Verhalten des Marktes, die auf günstige Gelegenheiten für die Ausführung von Trades hinweisen. Am häufigsten ist der erste Schritt bei der Entwicklung eines Handelssystems die Erstellung eines technischen Indikators, der es erlaubt, benötigte Informationen im Preischart zu sehen. Der Artikel hilft Ihnen, eine Anforderungsspezifikation bei der Bestellung eines Indikators im Freelance zu erarbeiten.