Ein einfaches Beispiel zur Erstellung eins Indikators mittels Qualitativaussagenlogik (unscharfer oder fuzzy Logik)

Einleitung

Der Einsatz verschiedener Methoden zur Analyse der Finanzmärkte ist bei den Börsenhändlern in den zurückliegenden Jahren immer beliebter geworden. Auch ich möchte mein Scherflein dazu beitragen, indem ich demonstriere, wie man mit ein paar Zeilen Programmcode einen ordentlichen Indikator anlegen kann. Ganz nebenbei werde ich auch kurz auf die Grundlagen der „fuzzy logic“ genannten unscharfen oder Qualitativaussagenlogik eingehen.

Allen, denen das nicht genügt, und die sich für dieses Material interessieren, empfehle ich folgende Lektüre:

1.  A. Leonenkov Fuzzy Simulation in MATLAB and fuzzyTECH (nur russisch, dt. etwa Unscharfe Modellierung in MATLAB und fuzzyTECH).
2.  V. Botscharnikov Fuzzy Technology: Mathematical Background. Simulation Practice in Economics (nur russisch, dt. etwa Fuzzy-Technologie. Mathematische Grundlagen. Praxis der Modellierung in der Wirtschaft).
3.  S.N. Sivanandam, S. Sumathi, S.N. Deepa. Introduction to Fuzzy Logic using MATLAB. (Einführung in die Qualitativaussagenlogik mittels MATLAB)
4.  C. Kahraman, Hg. Fuzzy Engineering Economics with Applications (aus der Reihe Studies in Fuzziness and Soft Computing).

1. Grundlagen der Qualitativaussagenlogik

Wie erklärt man seinem Rechner für Menschen so elementare Aussagen wie „ein wenig mehr“, „zu schnell“ oder „fast nichts“? Das ist möglich und zwar mithilfe von Elementen unscharfer Mengen, um genau zu sein der so genannten „Zugehörigkeitsfunktionen“. Hie ist ein Beispiel aus dem Buch A. Leonenkovs:

Wir schreiben die Zugehörigkeitsfunktion für die Aussage „heißer Kaffee“: dazu müssen wir die Kaffeetemperatur in dem Bereich von 0 bis 100°C betrachten, da der Kaffee bei unter null Grad gefrieren und bei über 100 Grad verdampfen würde. Es ist offenkundig, dass eine Tasse Kaffee bei einer Temperatur von 20 Grad nicht als „heiß“ bezeichnet werden könnte, das heißt, die Funktion für die Zugehörigkeit des Kaffees zu der Kategorie „heiß“ würde eine Null ausgeben, während der Kaffee bei einer Temperatur von 70 Grad zweifelsohne der Kategorie „heiß“ zugerechnet würde, der Funktionswert wäre in diesem Falle „1“.

Hinsichtlich der Temperaturwerte zwischen diesen Grenzen verhält es sich nicht so eindeutig. Der Eine erachtet eine Tasse Kaffee mit einer Temperatur von 55 Grad vielleicht als „heiß“, während andere denken mögen, sie wäre doch „nicht ganz so heiß“. Das ist es was die „Unschärfe“ ausmacht.

Nichtsdestoweniger können wir uns ein Muster für eine Zugehörigkeitsfunktion vorstellen, und zwar für eine monoton steigende.

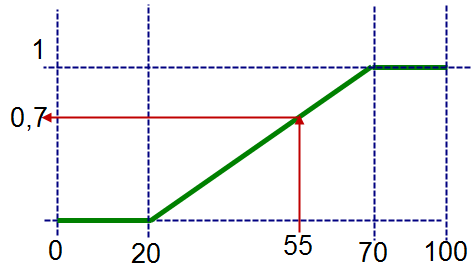
Die Abbildung oben zeigt eine „stückweise lineare“ Zugehörigkeitsfunktion.

Somit kann die Funktion mit folgendem analytischen Ausdruck aufgestellt werden:

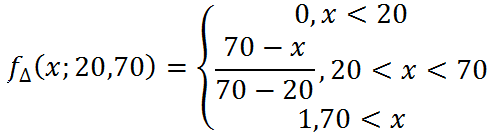
Vergleichbare Funktionen werden wir für unseren Indikator verwenden.

2. Die Zugehörigkeitsfunktion

Zur Aufgabe eines jeden technischen Indikators gehören in mehr oder weniger großem Umfang die Ermittlung der Marktlage zu einem gegebenen Zeitpunkt (gleichbleibender flat], auf- oder absteigender Trend) sowie die Erzeugung von Signalen für einen Geschäftsabschluss oder den Verzicht darauf. Wie bewerkstelligen wir das mithilfe von Zugehörigkeitsfunktionen? Nichts leichter als das.

Zunächst müssen wir die Randbedingungen festlegen. Die Randbedingung zur Bestimmung des „100-prozentig aufsteigenden Trends“ ist der Schnittpunkt des aus dem durchschnittlichen Kurs der entsprechenden Handelsperiode ermittelte EMA (H+L+C)/3 für den Zeitraum 2 mit dem oberen Rand des Umschlags-Indikators Envelopes mit den Parametern 8; 0,08, SMA und Close, wogegen der „100-prozentig absteigende Trend“ am Schnittpunkt desselben EMA mit dem unteren Rand des Envelopes-Indikators seine Randbedingung hat. Alles, was dazwischen liegt, betrachten wir als gleichbleibend oder „flat“. Zur Steigerung der Aussagekraft nehmen wir einen weiteren „Umschlag“ mit den Parametern 32; 0,15, SMA und Close hinzu. 

Das Ergebnis müssen zwei identische Zugehörigkeitsfunktionen sein. Als Signal für einen Kauf dient jede Situation, in der beide Funktionen gleich 1 sind, für den Verkauf entsprechend minus 1. Da es einfach ist, Diagramme mit einem Wertebereich von „-1“ bis „1“ anzulegen, erhalten wir unsere Abbildung mithilfe des arithmetischen Mittels der Ergebnisse zweier Funktionen F(x)= (f1(x)+f2(x))/2.

So sieht das resultierende Diagramm aus:

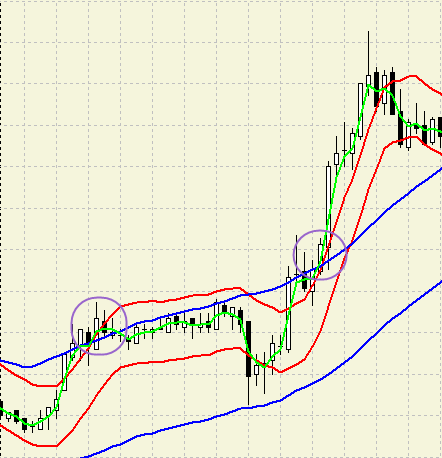
Die Zugehörigkeitsfunktion nimmt in diesem Fall folgende Gestalt an:

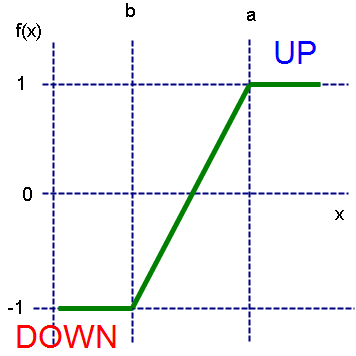
In analytischer Schreibweise liest sich das so:

,

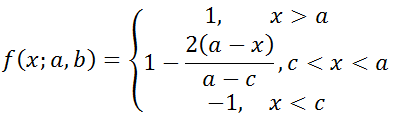mit a und b als oberer bzw. unterer „Umschlagsgrenze“ sowie х als Wert von EMA(2).

Mit der definierten Funktion machen wir uns jetzt an das Schreiben des Indikatorcodes.

3. Anlegen des Programmcodes

Zunächst müssen wir klären, was und wie wir es zeichnen möchten.

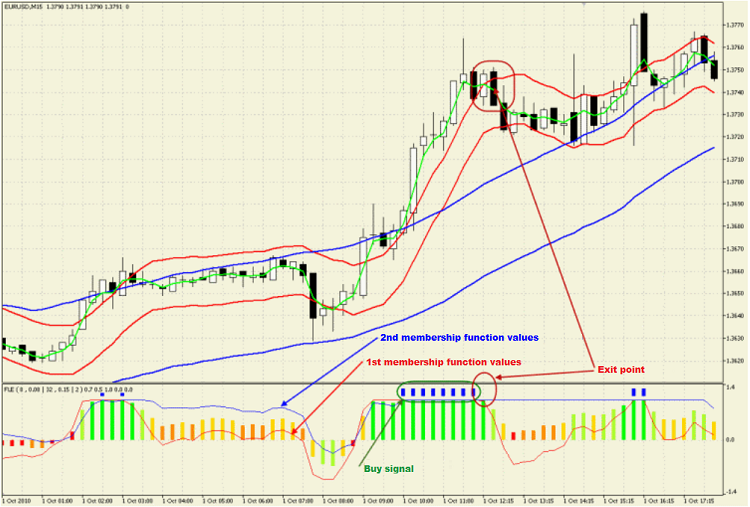
Die Ergebnisse der Berechnung der Zugehörigkeitsfunktion werden wir als rote bzw. blaue Linie ausgeben.

Das arithmetische Mittel wird als Histogramm ab der Nulllinie abgebildet und je nach Wert der resultierenden Funktion mit fünf Farben gefärbt.

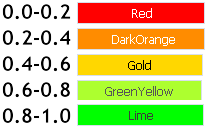
Dazu verwenden wir die Darstellungsart DRAW_COLOR_HISTOGRAM.

Zur Wiedergabe der Kauf- und Verkaufssignale zeichnen wir oberhalb der Balken des Histogramms, deren Wert gleich „1“ oder „-1“ ist, blaue und rote Rechtecke ein.

Jetzt ist es an der Zeit, das Bearbeitungsprogramm MetaEditor aufzurufen und endlich anzufangen: Neu->Benutzerdefinierter Indikator->Weiter... (New->Custom Indicator->Next...) Wir füllen das Eingabefeld „Parameter“ aus:

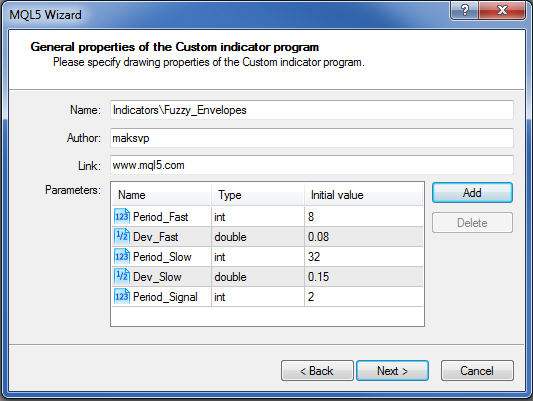
 Und legen die Zwischenspeicher (Puffer) an:

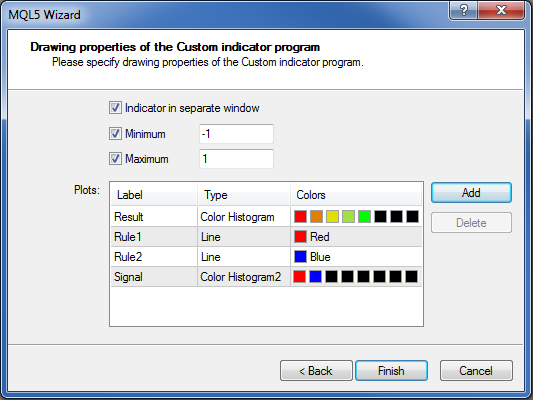
Nach Betätigen der Schaltfläche „Fertig“ erhalten wir den Quellcode und können beginnen, ihn zu verbessern.

Zunächst einmal legen wir die Anzahl der Zwischenspeicher fest. Sieben sind bereits von dem Assistenten angelegt worden (5 für Daten und 2 für Farben). Wir benötigen 5 weitere.

#property indicator_minimum -1.4 // Setting fractional values
#property indicator_maximum 1.4  // Expert Advisors wizard ignores fractional parts for some reason
#property indicator_buffers 12   // Changing the value from 7 to 12 (5 more buffers have been added)

Jetzt bearbeiten wir die Eingangsparameter:

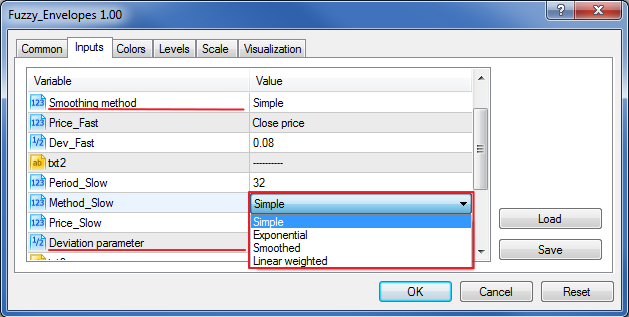
input string txt1="----------";
input int                  Period_Fast=8;
input ENUM_MA_METHOD        Method_Fast = MODE_SMA; /*Smoothing method*/ //moving average smoothing method 
input ENUM_APPLIED_PRICE    Price_Fast  = PRICE_CLOSE;
input double               Dev_Fast=0.08;
input string txt2="----------";
input int                  Period_Slow=32;
input ENUM_MA_METHOD        Method_Slow = MODE_SMA;
input ENUM_APPLIED_PRICE    Price_Slow  = PRICE_CLOSE;
input double               Dev_Slow=0.15;  /*Deviation parameter*/
input string txt3="----------";
input int                  Period_Signal=2;
input ENUM_MA_METHOD        Method_Signal = MODE_EMA;
input ENUM_APPLIED_PRICE    Price_Signal  = PRICE_TYPICAL;
input string txt4="----------";

Eine äußerst angenehme Neuerung sind die Kommentare hinter den deklarierten Variablen. Ihr Text wird in das Eingabefeld für die Indikatorparameter eingegeben.

Die Möglichkeit, Listen anzulegen, ist ebenfalls recht nützlich:

Wir belegen Variablen für die Bezeichner und Zwischenspeicher der Indikatoren vor:

int Envelopes_Fast;     // Fast envelope
int Envelopes_Slow;     // Slow envelope
int MA_Signal;          // Signal line

double Env_Fast_Up[];   // Fast envelope upper border
double Env_Fast_Dn[];   // Fast envelope lower border

double Env_Slow_Up[];   // Slow envelope upper border
double Env_Slow_Dn[];   // Slow envelope lower border

double Mov_Sign[];      // Signal line

Weiter geht es jetzt mit der Funktion OnInit().

Wir hübschen etwas auf, indem wir den Namen des Indikators angegeben und die überzähligen Dezimalnullen löschen:

IndicatorSetInteger(INDICATOR_DIGITS,1); // setting display accuracy, we do not need some outstanding accuracy values 
string name;                           // indicator name 
StringConcatenate(name, "FLE ( ", Period_Fast, " , ", Dev_Fast, " | ", Period_Slow, " , ", Dev_Slow, " | ", Period_Signal, " )"); 
IndicatorSetString(INDICATOR_SHORTNAME,name);

und die fehlenden Zwischenspeicher hinzufügen:

SetIndexBuffer(7,Env_Fast_Up,INDICATOR_CALCULATIONS);
SetIndexBuffer(8,Env_Fast_Dn,INDICATOR_CALCULATIONS);
SetIndexBuffer(9,Env_Slow_Up,INDICATOR_CALCULATIONS);
SetIndexBuffer(10,Env_Slow_Dn,INDICATOR_CALCULATIONS);
SetIndexBuffer(11,Mov_Sign,INDICATOR_CALCULATIONS);

Der Parameter INDICATOR_CALCULATIONS besagt, dass die Daten des Zwischenspeichers lediglich für die Zwischenberechnungen gedacht sind. Sie werden im Diagramm nicht angezeigt.

Schauen Sie sich an, wie die Indikatoren mit dem Farbpuffer deklariert werden:

SetIndexBuffer(4,SignalBuffer1,INDICATOR_DATA);      // All indicator buffers at first 
SetIndexBuffer(5,SignalBuffer2,INDICATOR_DATA);      // as this is Color Histogram2, then it has 2 data buffers
SetIndexBuffer(6,SignalColors,INDICATOR_COLOR_INDEX);// the color buffer comes next.

wir füllen die Bezeichner (handles) aus:

Envelopes_Fast = iEnvelopes(NULL,0,Period_Fast,0,Method_Fast,Price_Fast,Dev_Fast);
Envelopes_Slow = iEnvelopes(NULL,0,Period_Slow,0,Method_Slow,Price_Slow,Dev_Slow);
MA_Signal      = iMA(NULL,0,Period_Signal,0,Method_Signal,Price_Signal);

Die Funktion OnInit() hat ihre Schuldigkeit getan...

Jetzt legen wir die Funktion an, die den Wert für die Zugehörigkeitsfunktion berechnen wird:

double Fuzzy(double x,double a, double c)
{
double F;
     if (a<x)          F=1;                 // 100% uptrend
else if (x<=a && x>=c)  F=(1-2*(a-x)/(a-c));// Flat
else if (x<c)           F=-1;               // 100% downtrend
return (F);
}

Die Vorbereitungen sind abgeschlossen. Variablen und Zwischenspeicher sind deklariert, die Bezeichner zugeordnet.

Machen wir uns unmittelbar an die Hauptfunktion OnCalculate().

Zu Beginn schreiben wir die Werte der von uns benötigten Indikatoren in die Zwischenspeicher. Dazu verwenden wir die Funktion CopyBuffer():

CopyBuffer(Envelopes_Fast,  // Indicator handle
           UPPER_LINE,      // Indicator buffer
           0,              // The point to start 0 - from the very beginning
           rates_total,    // How many to be copied - All 
           Env_Fast_Up);   // The buffer the values are written in
// - the rest are done in a similar way
CopyBuffer(Envelopes_Fast,LOWER_LINE,0,rates_total,Env_Fast_Dn);
CopyBuffer(Envelopes_Slow,UPPER_LINE,0,rates_total,Env_Slow_Up);
CopyBuffer(Envelopes_Slow,LOWER_LINE,0,rates_total,Env_Slow_Dn);
CopyBuffer(MA_Signal,0,0,rates_total,Mov_Sign);

 Hier muss der Code zur Optimierung der Berechnung eingefügt werden (Neuberechnung nur des letzten Balkens).

// declaring start variable for storing the index of the bar, recalculation of the indicator buffers will be
// carried out from.

int start;              
if (prev_calculated==0)  // in case no bars have been calculated
    {
    start = Period_Slow; // not all indicators have been calculated up to this value, therefore, there is no point in executing the code
    }
else start=prev_calculated-1;

for (int i=start;i<rates_total;i++)
      {
      // All remaining code will be written here
      }

Jetzt fehlt nur noch ein winziges bisschen Code.

Wir legen die Parameter x, a und b fest, nehmen die Berechnung des Wertes für die Zugehörigkeitsfunktion vor und legen ihn in dem entsprechenden Zwischenspeicher ab:

double x = Mov_Sign[i]; // Signal
// Setting the first membership function parameters:
double a1 = Env_Fast_Up[i]; // Upper border
double b1 = Env_Fast_Dn[i];
// setting the first membership function value and writing it to the buffer
Rule1Buffer[i] = Fuzzy(x,a1,b1);
// Setting the second membership function parameters:
double a2 = Env_Slow_Up[i]; // Upper border
double b2 = Env_Slow_Dn[i];
// setting the second membership function value and writing it to the buffer
Rule2Buffer[i] = Fuzzy(x,a2,b2);

Die zwei Indikatorzeilen wurden angelegt.

Jetzt berechnen wir das Ergebnis.

ResultBuffer[i] = (Rule1Buffer[i]+Rule2Buffer[i])/2;

Weiterhin füllen wir die Balken des Histogramms mit den entsprechenden Farben: da wir derer fünf haben, kann ResultColors[i] jeden Wert zwischen 0 und 4 jeweils einschließlich annehmen.

Generell sind bis zu 64 Farben möglich. Hier können wir also unserer Kreativität freien Lauf lassen.

for (int ColorIndex=0;ColorIndex<=4;ColorIndex++) 
    { 
    if (MathAbs(ResultBuffer[i])>0.2*ColorIndex && MathAbs(ResultBuffer[i])<=0.2*(ColorIndex+1)) 
        { 
        ResultColors[i] = ColorIndex; 
        break; 
        } 
    }

Außerdem zeichnen wir die Rechtecke für die Signale. Dazu benötigen wir die Darstellungsart DRAW_COLOR_HISTOGRAM2.

Sie verfügt über zwei Datenpuffer, zwischen denen der Histogrammbalken angelegt wird, sowie einen Farbpuffer.

Die Werte der Datenpuffer sind stets konstant: 1,1 und 1,3 für ein Kaufsignal bzw. -1,1 und -1,3 für ein Verkaufssignal.

Der Wert EMPTY_VALUE entspricht dem Nichtvorhandensein eines Signals.

      if (ResultBuffer[i]==1)
        {
        SignalBuffer1[i]=1.1;
        SignalBuffer2[i]=1.3;
        SignalColors[i]=1;
        }
      else if (ResultBuffer[i]==-1)
        {
        SignalBuffer1[i]=-1.1;
        SignalBuffer2[i]=-1.3;
        SignalColors[i]=0;
        }
      else
        {
        SignalBuffer1[i]=EMPTY_VALUE;
        SignalBuffer2[i]=EMPTY_VALUE;
        SignalColors[i]=EMPTY_VALUE;
        }

Wir betätigen die Schaltfläche „Kompilieren“, et voilà!

Fazit

Was kann sonst noch hinzugefügt werden? In diesem Beitrag wurde der grundlegendste Zugang zur Qualitativaussagenlogik vorgestellt.

Er lässt genügend Spielraum für weitere Experimente. Zum Beispiel könnten wir die folgende Funktion verwenden:

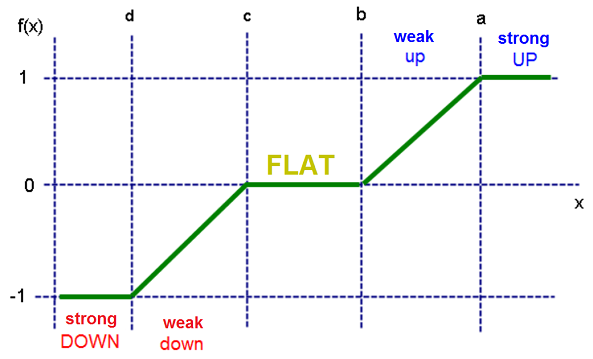
Ich bin sicher, es wird Ihnen nicht schwer fallen, den analytischen Ausdruck dafür zu schreiben und die geeigneten Bedingungen zu finden.

Viel Erfolg!