Funktionsentwicklung mit Python und MQL5 (Teil I): Vorhersage gleitender Durchschnitte für weitreichende AI-Modelle
Bei der Anwendung von KI auf eine beliebige Aufgabe müssen wir unser Bestes tun, um dem Modell so viele nützliche Informationen über die reale Welt zu geben, wie wir können. Um unseren KI-Modellen verschiedene Eigenschaften des Marktes zu beschreiben, müssen wir die Eingabedaten manipulieren und umwandeln; dieser Prozess wird als Feature Engineering bezeichnet. In dieser Artikelserie erfahren Sie, wie Sie Ihre Marktdaten transformieren können, um die Fehlerquote Ihrer Modelle zu verringern. Heute werde ich mich darauf konzentrieren, wie Sie gleitende Durchschnitte verwenden können, um die Prognosespanne Ihrer KI-Modelle auf eine Weise zu vergrößern, die eine vollständige Kontrolle und ein angemessenes Verständnis der globalen Wirksamkeit der Strategie ermöglicht.
Überblick über die Strategie
Als wir das letzte Mal über die Vorhersage gleitender Durchschnitte mit KI sprachen, lieferte ich Beweise dafür, dass die Werte gleitender Durchschnitte für unsere KI-Modelle leichter vorherzusagen sind als künftige Kursniveaus; der Link zu diesem Artikel ist hier zu finden. Damit wir jedoch sicher sein können, dass unsere Ergebnisse signifikant sind, habe ich zwei identische KI-Modelle auf mehr als 200 verschiedene Marktsymbole trainiert und die Genauigkeit der Preisprognose mit der Genauigkeit der Prognose des gleitenden Durchschnitts verglichen. Die Ergebnisse scheinen zu zeigen, dass unsere Genauigkeit im Durchschnitt um 34 % sinkt, wenn wir den Preis über die gleitenden Durchschnitte prognostizieren.
Im Durchschnitt können wir bei der Prognose der gleitenden Durchschnitte mit einer Genauigkeit von 70 % rechnen, während wir bei der Kursprognose eine Genauigkeit von 52 % erwarten. Wir alle wissen, dass der Indikator des gleitenden Durchschnitts je nach Zeitraum den Kursen nicht sehr genau folgt. So kann der Kurs beispielsweise über 20 Kerzen hinweg fallen, während die gleitenden Durchschnitte im gleichen Zeitraum steigen. Diese Divergenz ist für uns unerwünscht, da wir zwar die Richtung des gleitenden Durchschnitts korrekt vorhersagen können, der Preis aber abweichen kann. Bemerkenswerterweise haben wir festgestellt, dass die Rate der Divergenz über alle Märkte hinweg konstant bei 31 % liegt, und unsere Fähigkeit, Divergenzen vorherzusagen, lag im Durchschnitt bei 68 %.
Darüber hinaus betrug die Varianz unserer Fähigkeit, Divergenzen vorherzusagen, 0,000041 und die des Auftretens von Divergenzen 0,000386. Dies zeigt, dass unser Modell in der Lage ist, sich selbst mit ausreichender Qualifikation zu korrigieren. Mitglieder der Community, die KI in langfristigen Handelsstrategien einsetzen wollen, sollten diesen alternativen Ansatz für höhere Zeiträume in Betracht ziehen. Wir beschränken uns vorerst auf die M1, weil dieser Zeitrahmen sicherstellt, dass wir über genügend Daten für alle 297 Märkte verfügen, um faire Vergleiche anstellen zu können.
Es gibt viele mögliche Gründe, warum die gleitenden Durchschnitte leichter vorherzusagen sind als der Kurs selbst. Das mag daran liegen, dass die Vorhersage gleitender Durchschnitte eher der Idee der linearen Regression entspricht als die Preisvorhersage, denn die lineare Regression geht davon aus, dass die Daten eine lineare Kombination (Summe) mehrerer Eingaben sind: Gleitende Durchschnitte sind eine Summierung früherer Kurswerte, d. h. die lineare Annahme ist zutreffend. Der Preis selbst ist keine einfache Summierung von Variablen aus der realen Welt, sondern eine komplexe Beziehung zwischen vielen Variablen.
Die ersten Schritte
Zunächst müssen wir unsere Standardbibliotheken für wissenschaftliches Rechnen in Python importieren
#Load the libraries we need import pandas as pd import numpy as np import MetaTrader5 as mt5 from sklearn.model_selection import TimeSeriesSplit,cross_val_score from sklearn.linear_model import LogisticRegression,LinearRegression import matplotlib.pyplot as plt
und unsern MetaTrader 5 Terminal initialisieren.
#Initialize the terminal
mt5.initialize() Wie viele Symbole haben wir zur Verfügung?
#The total number of symbols we have print(f"Total Symbols Available: ",mt5.symbols_total())
Ermittelung der Namen aller Symbole.
#Get the names of all pairs symbols = mt5.symbols_get() idx = [s.name for s in symbols]
Wir erstellen einen Datenrahmen, um unsere Genauigkeitsstufen für alle Symbole zu speichern.
global_params = pd.DataFrame(index=idx,columns=["OHLC Error","MAR Error","Noise Levels","Divergence Error"]) global_params
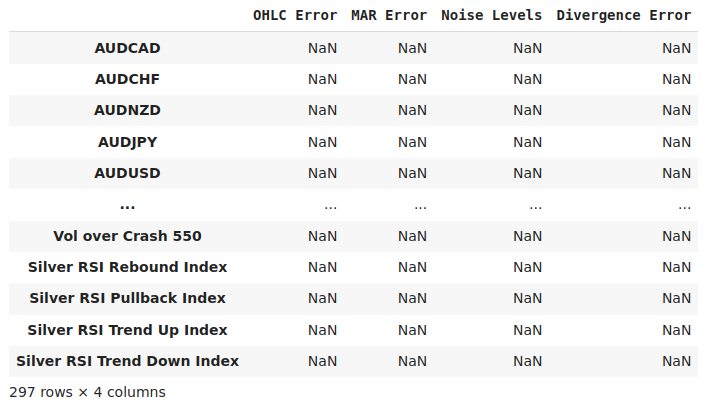
Abb. 1: Unser Datenrahmen, der unsere Genauigkeitsstufen für alle Märkte in unserem Terminal speichert
Definieren wir unser Zeitserien-Splitobjekt
#Define the time series split object tscv = TimeSeriesSplit(n_splits=5,gap=10)
und messen unsere Genauigkeit bei allen Symbolen.
#Iterate over all symbols for i in np.arange(global_params.dropna().shape[0],len(idx)): #Fetch M1 Data data = pd.DataFrame(mt5.copy_rates_from_pos(cols[i],mt5.TIMEFRAME_M1,0,50000)) data.rename(columns={"open":"Open","high":"High","low":"Low","close":"Close"},inplace=True) #Define our period period = 10 #Add the classical target data.loc[data["Close"].shift(-period) > data["Close"],"OHLC Target"] = 1 #Calculate the returns data.loc[:,["Open","High","Low","Close"]] = data.loc[:,["Open","High","Low","Close"]].diff(period) data["RMA"] = data["Close"].rolling(period).mean() #Calculate our new target data.dropna(inplace=True) data.reset_index(inplace=True,drop=True) data.loc[data["RMA"].shift(-period) > data["RMA"],"New Target"] = 1 data = data.iloc[0:-period,:] #Calculate the divergence target data.loc[data["OHLC Target"] != data["New Target"],"Divergence Target"] = 1 #Noise ratio global_params.iloc[i,2] = data.loc[data["New Target"] != data["OHLC Target"]].shape[0] / data.shape[0] #Test our accuracy predicting the future close price score = cross_val_score(LogisticRegression(),data.loc[:,["Open","High","Low","Close"]],data["OHLC Target"],cv=tscv) global_params.iloc[i,0] = score.mean() #Test our accuracy predicting the moving average of future returns score = cross_val_score(LogisticRegression(),data.loc[:,["Open","Close","RMA"]],data["New Target"],cv=tscv) global_params.iloc[i,1] = score.mean() #Test our accuracy predicting the future divergence between price and its moving average score = cross_val_score(LogisticRegression(),data.loc[:,["Open","Close","RMA"]],data["Divergence Target"],cv=tscv) global_params.iloc[i,3] = score.mean() print(f"{((i/len(idx)) * 100)}% complete") #We are done print("Done")
Done
Analyse der Ergebnisse
Nachdem wir nun unsere Marktdaten abgerufen und unser Modell für die beiden Ziele bewertet haben, wollen wir nun die Ergebnisse unseres Tests für alle Märkte zusammenfassen. Wir beginnen mit einer Zusammenfassung unserer Genauigkeit bei der Vorhersage der Veränderung des zukünftigen Schlusskurses. Die folgende Abbildung 2 zeigt die Zusammenfassung der Vorhersage der Veränderung des künftigen Schlusskurses. Die rote horizontale Linie stellt die 50%ige Genauigkeitsschwelle dar. Unsere durchschnittliche Genauigkeit mit dieser Technik ist durch die blaue horizontale Linie dargestellt. Wie wir sehen können, ist unsere durchschnittliche Genauigkeit nicht signifikant weit von der 50%-Schwelle entfernt, was keine ermutigende Information ist.
Fairerweise muss man aber auch feststellen, dass einige Märkte deutlich über dem Durchschnitt liegen und mit einer Genauigkeit von mehr als 65 % vorhergesagt werden können. Das ist beeindruckend, aber es erfordert auch weitere Untersuchungen, um festzustellen, ob die Ergebnisse aussagekräftig sind oder ob es sich um einen Zufall handelt.
global_params.iloc[:,0].plot()
plt.title("OHLC Accuracy")
plt.xlabel("Market")
plt.ylabel("5-fold Accuracy %")
plt.axhline(global_params.iloc[:,0].mean(),linestyle='--')
plt.axhline(0.5,linestyle='--',color='red') 
Abb. 2: Unsere durchschnittliche Genauigkeit bei der Preisvorhersage
Wenden wir uns nun der Genauigkeit zu, mit der wir die Veränderung der gleitenden Durchschnitte vorhersagen. Abbildung 3 fasst die Daten für uns zusammen. Auch hier stellt die rote Linie den Schwellenwert von 50 % dar, die goldene Linie unsere durchschnittliche Genauigkeit bei der Vorhersage von Änderungen des Preisniveaus und die blaue Linie unsere durchschnittliche Genauigkeit bei der Vorhersage von Änderungen des gleitenden Durchschnitts. Einfach zu sagen, dass unser Modell die gleitenden Durchschnitte besser vorhersagen kann, ist eine Untertreibung. Ich denke, es ist nicht mehr Gegenstand der Debatte, sondern einfach eine Tatsache, dass unsere Modelle bestimmte Indikatoren besser vorhersagen können als den Preis.
global_params.iloc[:,1].plot()
plt.title("Moving Average Returns Accuracy")
plt.xlabel("Market")
plt.ylabel("5-fold Accuracy %")
plt.axhline(global_params.iloc[:,1].mean(),linestyle='--')
plt.axhline(global_params.iloc[:,0].mean(),linestyle='--',color='orange')
plt.axhline(0.5,linestyle='--',color='red') 
Abb. 3: Unsere Genauigkeit bei der Vorhersage der Veränderung des gleitenden Durchschnitts
Beobachten wir nun die Geschwindigkeit, mit der der Kurs und der gleitende Durchschnitt auseinanderklaffen. Divergenzwerte von annähernd 50 % sind schlecht, denn das bedeutet, dass wir nicht sicher sein können, ob sich der Kurs und der gleitende Durchschnitt gemeinsam oder in entgegengesetzte Richtungen bewegen werden. Zu unserem Glück war das Rauschen (noise) auf allen von uns untersuchten Märkten konstant. Das Rauschen der Kurse schwankte zwischen 35 % und 30 %.
global_params.iloc[:,2].plot()
plt.title("Noise Level")
plt.xlabel("Market")
plt.ylabel("Percentage of Divergence:Price And Moving Average")
plt.axhline(global_params.iloc[:,2].mean(),linestyle='--') 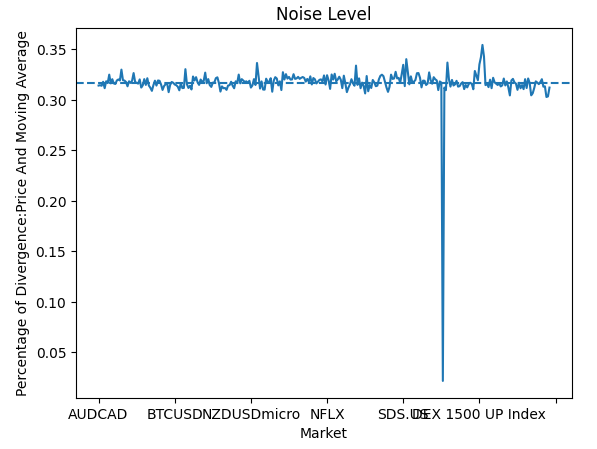
Abb. 4: Visualisierung unserer Rauschens in allen Märkten
Wenn zwei Variablen ein nahezu konstantes Verhältnis aufweisen, kann dies ein Zeichen dafür sein, dass eine Beziehung besteht, die wir modellieren können. Beobachten wir, wie gut wir Divergenzen zwischen dem Preis und dem gleitenden Durchschnitt vorhersagen können. Unser Grundprinzip ist einfach: Wenn unser Modell vorhersagt, dass der gleitende Durchschnitt fallen wird, können wir dann vernünftig vorhersagen, ob sich der Preis in die gleiche Richtung bewegen wird oder ob er vom gleitenden Durchschnitt abweicht? Es stellt sich heraus, dass wir Divergenzen mit einer zuverlässigen Genauigkeit von durchschnittlich fast 70 % vorhersagen können.
global_params.iloc[:,3].plot()
plt.title("Divergence Accuracy")
plt.xlabel("Market")
plt.ylabel("5-fold Accuracy %")
plt.axhline(global_params.iloc[:,3].mean(),linestyle='--') 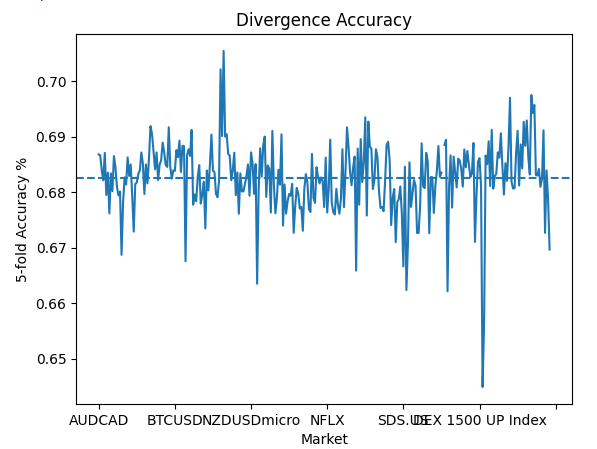
Abb. 5: Unsere Genauigkeit bei der Vorhersage von Divergenzen zwischen dem Preis und dem gleitenden Durchschnitt
Wir können unsere Ergebnisse auch in tabellarischer Form zusammenfassen. So können wir unsere Genauigkeit zwischen den Marktrenditen und einem gleitenden Durchschnitt der Renditen leicht vergleichen. Auch wenn unser gleitender Durchschnitt dem Preis „hinterherhinkt“, ist unsere Genauigkeit bei der Vorhersage von Umkehrungen immer noch deutlich höher als bei der Vorhersage des Preises selbst.
| Kennzahl | Genauigkeit |
|---|---|
| Fehler der Rückgabe (OHLC) | 0.525353 |
| Fehler des gleitenden Durchschnitts der Renditen (MAR) | 0.705468 |
| Ausmaß des Rauschens (noise) | 0.317187 |
| Fehler der Divergenz (divergence) | 0.682069 |
Schauen wir uns an, auf welchen Märkten unser Modell am besten abgeschnitten hat.
global_params.sort_values("MAR Error",ascending=False) 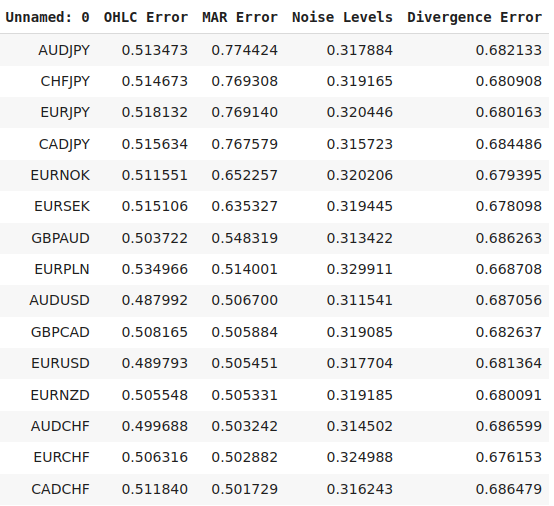
Abb. 6: Unsere leistungsstärksten Märkte
Optimierung für unseren leistungsstärksten Markt
Lassen Sie uns nun unseren gleitenden Durchschnittsindikator für einen der Märkte entwickeln und anpassen, auf denen unsere Performance am größten ist. Wir werden unser neu entwickeltes Merkmal auch visuell mit den klassischen Merkmalen vergleichen. Wir beginnen mit der Spezifizierung unseres ausgewählten Marktes.
symbol = "AUDJPY" Stellen wir sicher, dass das Terminal erreichbar ist.
#Reach the terminal
mt5.initialize() Jetzt holen wir und die Marktdaten
data = pd.DataFrame(mt5.copy_rates_from_pos(symbol,mt5.TIMEFRAME_D1,365*2,5000))
und importieren die benötigten Bibliotheken.
#Standard libraries import seaborn as sns from mpl_toolkits.mplot3d import Axes3D from sklearn.linear_model import LinearRegression from sklearn.neural_network import MLPRegressor from sklearn.metrics import mean_squared_error from sklearn.model_selection import cross_val_score,TimeSeriesSplit
Wir definieren Anfangs- und Endpunkt für unsere Periodenberechnung und unseren Prognosehorizont und vergewissern uns, dass beide Eingänge die gleiche Größe haben, sonst bricht unser Code ab.
#Define the input range x_min , x_max = 2,100 #Look ahead y_min , y_max = 2,100 #Period
Wir wählen unseren Eingabebereich in 5er-Schritten, damit unsere Berechnungen detailliert und kostengünstig sind.
#Sample input range uniformly x_axis = np.arange(x_min,x_max,2) #Look ahead y_axis = np.arange(y_min,y_max,2) #Period
Wir erstellen ein Maschengitter mit unserer x_Achse und y_Achse. Das Maschengitter besteht aus zwei zweidimensionalen Feldern, die alle möglichen Kombinationen von Perioden der Vorhersagehorizonte definieren, die wir bewerten möchten.
#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis) Als Nächstes benötigen wir eine Funktion, die unsere Marktdaten abruft und sie für die Auswertung kennzeichnet.
def clean_data(look_ahead,period): #Fetch the data from our terminal and clean it up data = pd.DataFrame(mt5.copy_rates_from_pos('AUDJPY',mt5.TIMEFRAME_D1,365*2,5000)) data['time'] = pd.to_datetime(data['time'],unit='s') data['MA'] = data['close'].rolling(period).mean() #Transform the data #Target data['Target'] = data['MA'].shift(-look_ahead) - data['MA'] #Change in price data['close'] = data['close'] - data['close'].shift(period) #Change in MA data['MA'] = data['MA'] - data['MA'].shift(period) data.dropna(inplace=True) data.reset_index(drop=True,inplace=True) return(data)
Die folgende Funktion führt eine 5-fache Kreuzvalidierung für unser KI-Modell durch.
#Evaluate the objective function def evaluate(look_ahead,period): #Define the model model = LinearRegression() #Define our time series split tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) temp = clean_data(look_ahead,period) score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv)) return(score)
Schließlich unsere Zielfunktion. Unsere Zielfunktion ist einfach der 5-fache Validierungsfehler unseres Modells unter den neuen Einstellungen, die wir bewerten wollen. Erinnern Sie sich daran, dass wir versuchen, den optimalen Abstand in die Zukunft zu finden, den unser Modell vorhersagen soll, und dass wir außerdem versuchen, den Zeitraum zu finden, für den wir Preisänderungen berechnen sollen.
#Define the objective def objective(x,y): #Define the output matrix results = np.zeros([x.shape[0],y.shape[0]]) #Fill in the output matrix for i in np.arange(0,x.shape[0]): #Select the rows look_ahead = x[i] period = y[i] for j in np.arange(0,y.shape[0]): results[i,j] = evaluate(look_ahead[j],period[j]) return(results)
Wir werden die Beziehung unseres Modells zum Markt bewerten, wenn wir versuchen, die Veränderung des Preisniveaus direkt vorherzusagen. Abbildung 7 zeigt die Beziehung zwischen unserem Modell und der Preisänderung, während Abbildung 8 die Beziehung zwischen unserem Modell und der Änderung des gleitenden Durchschnitts zeigt. Der weiße Punkt in beiden Diagrammen symbolisiert die Kombination von Eingaben, die für uns den geringsten Fehler ergab.
res = objective(x,y) res = np.abs(res)
Die beste Leistung unseres Modells bei der Vorhersage der täglichen Rendite des AUDJPY. Die Daten zeigen, dass wir bei der Vorhersage künftiger Preisveränderungen bestenfalls einen Schritt in die Zukunft prognostizieren können. Menschliche Händler schauen nicht einfach nur einen Schritt voraus, wenn sie ihre Trades platzieren. Die Ergebnisse, die wir durch die direkte Vorhersage von Marktrenditen erzielt haben, schränken also unseren Ansatz ein und führen dazu, dass unsere Modelle auf die nächste Kerze fixiert sind.
plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting AUDJPY Daily Return") 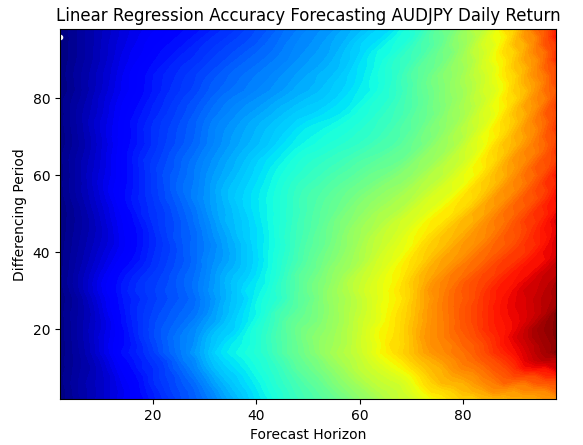
Abb. 7: Visualisierung der Fähigkeit unseres Modells, zukünftige Preisniveaus zu prognostizieren
Sobald wir damit beginnen, die Veränderung des gleitenden Durchschnitts zu prognostizieren und nicht mehr die Veränderung des Preises, können wir beobachten, dass sich unser optimaler Prognosehorizont nach rechts verschiebt. Abbildung 8 unten zeigt, dass wir durch die Vorhersage der Veränderung der gleitenden Durchschnitte nun 22 Schritte in die Zukunft prognostizieren können, während wir bei der Vorhersage der Preisveränderung nur einen Schritt in die Zukunft gehen.
plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting AUDJPY Daily Moving Average Return") 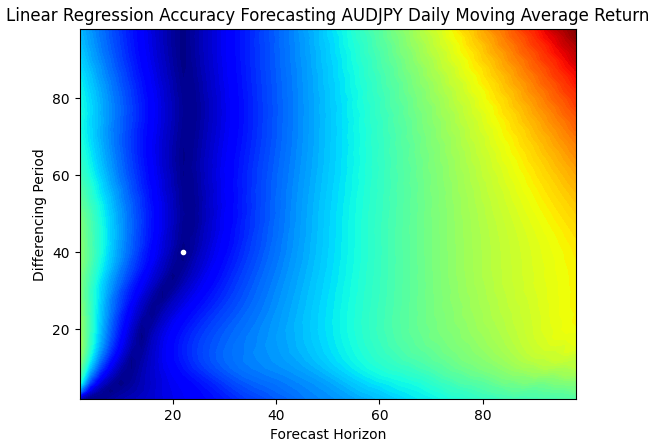
Abb. 8: Visualisierung der Fähigkeit unseres Modells, zukünftige gleitende Durchschnittswerte zu prognostizieren
Noch beeindruckender ist, dass unsere Fehlerquote an den optimalen Punkten bei beiden Zielen identisch war. Mit anderen Worten, es ist für unser Modell genauso einfach, die Veränderung des gleitenden Durchschnitts 40 Schritte in die Zukunft vorherzusagen, wie es für unser Modell ist, die Veränderung des Preises 1 Schritt in die Zukunft vorherzusagen. Die Vorhersage des gleitenden Durchschnitts bietet daher eine größere Reichweite, ohne den Fehler unserer Vorhersagen zu erhöhen.
Wenn wir die Ergebnisse unseres Tests in 3D visualisieren, wird der Unterschied zwischen den beiden Zielen deutlich. Die nachstehende Abbildung 9 zeigt die Beziehung zwischen den Veränderungen des Preisniveaus und den Prognoseparametern für unser Modell. Aus den Daten lässt sich ein klarer Trend ablesen: Je weiter wir in die Zukunft schauen, desto schlechter werden unsere Ergebnisse. Wenn wir unsere KI-Modelle auf diese Weise konzipieren, sind sie daher etwas „kurzsichtig“ und können keine vernünftigen Vorhersagen für Intervalle von mehr als 20 treffen.
Abbildung 10 zeigt die Beziehung zwischen unserem Modell und seinem Fehler bei der Vorhersage der Veränderungen der gleitenden Durchschnitte. Das Oberflächendiagramm weist wünschenswerte Eigenschaften auf. Es ist deutlich zu erkennen, dass unsere Fehlerquoten gleichmäßig bis zu einem Minimum sinken und dann wieder ansteigen, je weiter wir in die Zukunft prognostizieren und den Zeitraum für die Berechnung der Veränderung des gleitenden Durchschnitts erhöhen. Diese visuelle Demonstration zeigt, wie viel einfacher es für unser Modell ist, den gleitenden Durchschnitt vorherzusagen, als den Preis.
#Create a surface plot fig , ax = plt.subplots(subplot_kw={"projection":"3d"}) fig.set_size_inches(8,8) ax.plot_surface(x,y,optimal_nn_res,cmap="jet")
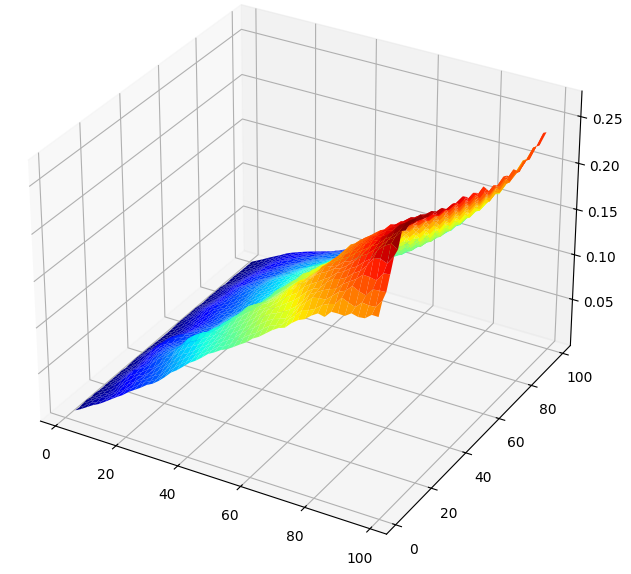
Abb. 9: Visualisierung der Beziehung zwischen unserem Modell und den Veränderungen des Tageskurses des AUDJPY.
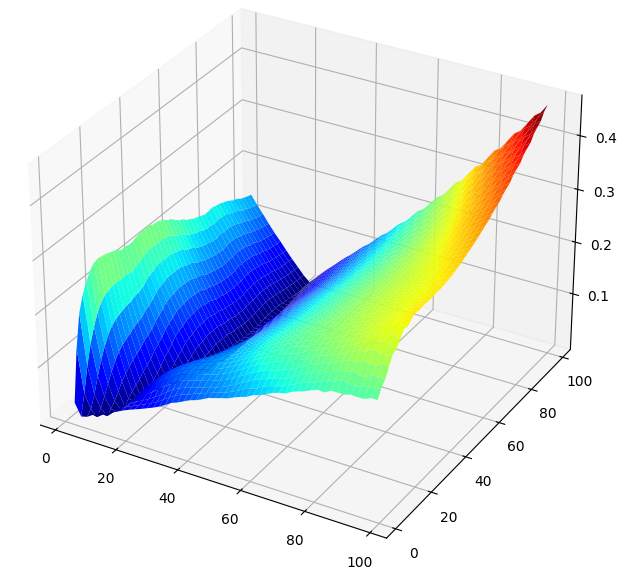
Abb. 10: Die Beziehung zwischen unserem Modell und den Veränderungen des gleitenden Durchschnittswerts für das Paar AUDJPY.
Nichtlineare Transformationen: Entrauschen von Wavelets
Bislang haben wir nur lineare Transformationen auf unsere Daten angewandt. Wir können sogar noch tiefer gehen und nichtlineare Transformationen auf die Eingabedaten des Modells anwenden. Die Entwicklung von Merkmalen ist manchmal einfach ein Prozess von Versuch und Irrtum. Wir haben nicht immer die Garantie, dass wir bessere Ergebnisse erzielen. Daher wenden wir diese Transformationen ad hoc an, denn wir haben keine genaue Formel, die uns zeigt, welche Transformation zu einem bestimmten Zeitpunkt die beste“ ist.
Die Wavelet-Transformation ist ein mathematisches Werkzeug, mit dem sich eine Frequenz- und Zeitdarstellung von Daten erstellen lässt. Sie wird häufig in der Signal- und Bildverarbeitung eingesetzt, um das Rauschen von dem zu verarbeitenden Signal zu trennen. Nach der Transformation befinden sich unsere Daten im Frequenzbereich. Die Idee ist, dass das Rauschen in unseren Daten von den kleinen Frequenzwerten stammt, die durch die Transformation identifiziert werden. Alle Werte, die unter einem bestimmten Schwellenwert liegen, werden auf eine von 2 möglichen Arten auf 0 reduziert. Das Ergebnis ist eine spärliche Darstellung der Originaldaten.
Das Entrauschen von Wavelet hat mehrere Vorteile gegenüber anderen gängigen Verfahren wie der schnellen Fourier-Transformation (FFT). Die Fourier-Transformation stellt ein beliebiges Signal als Summierung von Sinus- und Kosinuswellen dar, falls Sie damit nicht vertraut sind. Leider filtert die Fourier-Transformation unsere hohen Frequenzwerte. Dies ist nicht immer wünschenswert, insbesondere bei Daten, deren Signal im Hochfrequenzbereich liegt. Da wir uns nicht sicher sind, ob unser Signal im Hoch- oder Niederfrequenzbereich liegt, benötigen wir eine Transformation, die flexibel genug ist, um diese Aufgabe auf unüberwachte Weise zu erfüllen. Durch die Wavelet-Transformation bleibt das Signal in den Daten erhalten, während das Rauschen so weit wie möglich herausgefiltert wird.
Um uns zu folgen, stellen Sie sicher, dass Sie scikit learn image und seine Abhängigkeit PyWavelets installiert haben. Für Leser, die eine vollständige Handelsanwendung in MQL5 erstellen möchten, kann sich die Implementierung und Fehlerbehebung der Transformation von Grund auf als zu aufwändig erweisen. Es ist einfacher für uns, ohne sie voranzukommen. Und für Leser, die mit Hilfe der Python-Bibliothek eine Schnittstelle zum Terminal herstellen möchten, ist die Transformation ein Werkzeug, das man in sein Arsenal aufnehmen sollte.
Wir können die Veränderung der Validierungsgenauigkeit vergleichen, um zu sehen, ob die Transformation unserem Modell hilft, und das tut sie. Beachten Sie, dass wir die Transformation nur auf die Eingaben des Modells und nicht auf das Ziel anwenden, das Ziel bleibt erhalten. Es ist festzustellen, dass unsere Validierungsgenauigkeit tatsächlich gesunken ist. Wir verwenden die Wavelet-Transformation mit einem harten Schwellenwert, sodass alle Rauschkoeffizienten auf 0 gesetzt werden. Alternativ könnte man auch einen weichen Schwellenwert verwenden, der die Rauschkoeffizienten auf 0 lenkt, sie aber nicht exakt auf 0 setzt.
#Benchmark Score np.mean(cross_val_score(LinearRegression(),data.loc[:,["MA"]],data["Target"]))
#Wavelet denoising data["Denoised"] = denoise_wavelet( data["MA"], method='BayesShrink', mode='hard', rescale_sigma=True, wavelet_levels = 3, wavelet='sym5' ) np.mean(cross_val_score(LinearRegression(),np.sqrt(np.log(data.loc[:,["Denoised"]])),data["Target"]))
Erstellen maßgeschneiderter AI-Modelle
Da wir nun die idealen Parameter für die Zukunftsprognose und den optimalen Zeitraum für den gleitenden Durchschnitt kennen, können wir uns auf den nächsten Schritt konzentrieren. Wir holen unsere Marktdaten direkt vom MetaTrader 5-Terminal, um sicherzustellen, dass unsere KI-Modelle mit denselben Indikatorwerten trainiert werden, die sie auch beim realen Handel beobachten werden. Wir wollen die Erfahrung des realen Handels so gut wie möglich nachahmen.
Unsere gleitende Durchschnittsperiode im Skript entspricht der idealen gleitenden Durchschnittsperiode, die wir oben berechnet haben. Zusätzlich werden wir auch RSI-Werte von unserem Terminal abrufen, um das Verhalten unseres KI-Handelsroboters zu stabilisieren. Indem wir uns auf die Vorhersagen von zwei separaten Indikatoren anstelle von einem stützen, kann unser KI-Modell im Laufe der Zeit stabiler sein.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Inputs | //+------------------------------------------------------------------+ input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int ma_handler,rsi_handler; double ma_reading[],rsi_reading[]; //+------------------------------------------------------------------+ //| On start function | //+------------------------------------------------------------------+ void OnStart() { //--- Load indicator ma_handler = iMA(Symbol(),PERIOD_CURRENT,40,0,MODE_SMA,PRICE_CLOSE); rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,30,PRICE_CLOSE); //--- Load the indicator values CopyBuffer(ma_handler,0,0,size,ma_reading); CopyBuffer(rsi_handler,0,0,size,rsi_reading); ArraySetAsSeries(ma_reading,true); ArraySetAsSeries(rsi_reading,true); //--- File name string file_name = "Market Data " + Symbol() +" MA RSI " + " As Series.csv"; //--- Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close","MA","RSI"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), ma_reading[i], rsi_reading[i] ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Nachdem wir unser Skript erstellt haben, können wir es einfach auf den gewünschten Markt ziehen und dort ablegen, um mit den Marktdaten zu arbeiten. Damit unsere Backtests aussagekräftig sind, haben wir die letzten 2 Jahre der Marktdaten aus der von uns erstellten CSV-Datei herausgenommen. Wenn wir also unsere Strategie von 2023 bis 2024 einem Backtest unterziehen, werden die Ergebnisse ein getreues Abbild der Leistung unseres Modells auf Daten sein, die es noch nicht gesehen hat.
#Read in the data
data = pd.read_csv("Market Data AUDJPY MA RSI As Series.csv")
#Let's drop the last two years of data. We'll use that to validate our model in the back test
data = data.iloc[365:-(365 * 2),:]
data
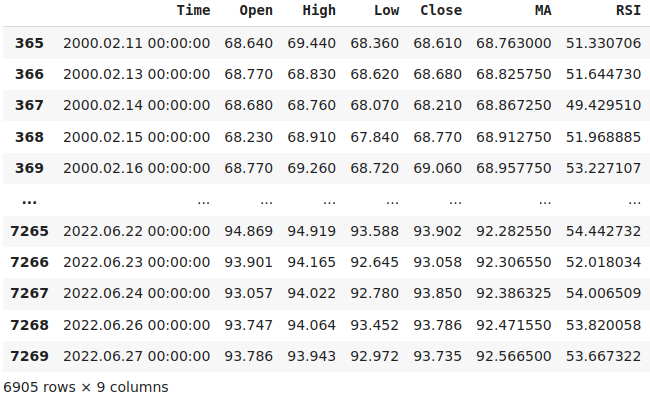
Abb. 11: Training unseres Modells über 22 Jahre Marktdaten, ohne den Zeitraum von 2023-2024.
Nun wollen wir unsere Daten für das maschinelle Lernen kennzeichnen. Wir wollen unserem Modell dabei helfen, die Preisveränderungen bei Veränderungen unserer technischen Indikatoren zu lernen. Um unserem Modell zu helfen, diese Beziehung zu erlernen, werden wir unsere Eingaben umwandeln, um den aktuellen Zustand des Indikators zu bezeichnen. Unser RSI-Indikator hat zum Beispiel 3 mögliche Zustände:
- Über 70.
- Unter 30.
- Zwischen 70 und 30.
#MA States data["MA 1"] = 0 data["MA 2"] = 0 data.loc[data["MA"] > data["MA"].shift(40),"MA 1"] = 1 data.loc[data["MA"] <= data["MA"].shift(40),"MA 2"] = 1 #RSI States data["RSI 1"] = 0 data["RSI 2"] = 0 data["RSI 3"] = 0 data.loc[data["RSI"] < 30,"RSI 1"] = 1 data.loc[data["RSI"] > 70,"RSI 2"] = 1 data.loc[(data["RSI"] >= 30) & (data["RSI"] <= 70),"RSI 3"] = 1 #Target data["Target"] = data["Close"].shift(-22) - data["Close"] data["MA Target"] = data["MA"].shift(-22) - data["MA"] #Clean up the data data = data.dropna() data = data.iloc[40:,:] data = data.reset_index(drop=True)
Jetzt können wir mit der Messung unserer Genauigkeit beginnen.
from sklearn.linear_model import Ridge from sklearn.model_selection import TimeSeriesSplit,cross_val_score
Die Anwendung dieser Transformationen ermöglicht es uns, die durchschnittliche Kursveränderung zu beobachten, wenn der RSI die 3 von uns festgelegten Zonen durchläuft. Die Koeffizienten unseres linearen Modells können als die durchschnittliche Preisänderung interpretiert werden, die mit jeder der 3 RSI-Zonen verbunden ist. Diese Ergebnisse stehen manchmal im Widerspruch zu den klassischen Lehren über die Verwendung des Indikators. Unser Ridge-Modell hat zum Beispiel gelernt, dass die Kurse fallen, wenn der RSI-Wert über 70 liegt, während die Kurse steigen, wenn der RSI-Wert unter 70 liegt.
#Our model can suggest optimal ways of using the RSI indicator #Our model has learned that on average price tends to fall the RSI reading is less than 30 and increases otherwises model = Ridge() model.fit(data.loc[:,["RSI 1","RSI 2","RSI 3"]] , data["Target"]) model.coef_
Unser Ridge-Modell kann zukünftige Kurse nur dann gut vorhersagen, wenn der aktuelle Stand des RSI bekannt ist.
#RSI state np.mean(cross_val_score(Ridge(),data.loc[:,["RSI 1","RSI 2","RSI 3"]] , data["Target"],cv=tscv))
Ebenso hat unser Modell seine eigenen Handelsregeln aus den Veränderungen der gleitenden Durchschnittsindikatoren gelernt. Der erste Koeffizient des Modells ist negativ, d. h. wenn der gleitende Durchschnitt über 40 Kerzen ansteigt, fällt er tendenziell. Und der zweite Koeffizient ist positiv. Wenn der gleitende 40-Perioden-Durchschnitt des AUDJPY-Tages über 40 Kerzen fällt, tendieren die historischen Daten, die wir in unserem Terminal abgerufen haben, dazu, danach zu steigen. Unser Modell hat aus den Daten eine Strategie des Rückkehrs zu Mitte gelernt.
#Our model can suggest optimal ways of using the RSI indicator #Our model has learned that on average price tends to fall the RSI reading is less than 30 and increases otherwises model = Ridge() model.fit(data.loc[:,["MA 1","MA 2"]] , data["Target"]) model.coef_
Unser Modell schneidet noch besser ab, wenn wir ihm den aktuellen Stand unseres gleitenden Durchschnittsindikators mitteilen.
#MA state np.mean(cross_val_score(Ridge(),data.loc[:,["MA 1","MA 2"]] , data["Target"],cv=tscv))
Umstellung auf ONNX
Nachdem wir nun die idealen Eingabeparameter für unsere gleitende Durchschnittsprognose gefunden haben, können wir nun unser Modell in das ONNX-Format konvertieren. Open Neural Network Exchange (ONNX) ermöglicht es uns, Modelle für maschinelles Lernen in einem sprachunabhängigen Rahmen zu erstellen. Das ONNX-Protokoll ist eine Open-Source-Initiative zur Schaffung einer universellen Standarddarstellung für Modelle des maschinellen Lernens, die es uns ermöglicht, Modelle des maschinellen Lernens in jeder beliebigen Sprache zu erstellen und einzusetzen, solange diese die ONNX-API vollständig übernimmt.
Lassen Sie uns zunächst die Daten abrufen, die wir benötigen, entsprechend den besten Eingaben, die wir gefunden haben.
#Fetch clean data new_data = clean_data(140,130)
Importieren wir die benötigten Bibliotheken,
import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
passen das RSI-Modell an alle vorhandenen Daten
#First we will export the RSI model rsi_model = Ridge() rsi_model.fit(data.loc[:,['RSI 1','RSI 2','RSI 3']],data.loc[:,'Target'])
und das Modell des gleitenden Durchschnitts an alle vorhandenen Daten an.
#Finally we will export the MA model ma_model = Ridge() ma_model.fit(data.loc[:,['MA 1','MA 2']],data.loc[:,'MA Target'])
Wir definieren die Eingabeform unseres Modells und speichern sie auf der Festplatte.
initial_types = [('float_input', FloatTensorType([1, 3]))]
onnx.save(convert_sklearn(rsi_model,initial_types=initial_types,target_opset=12),"AUDJPY D1 RSI AI F22 P40.onnx")
initial_types = [('float_input', FloatTensorType([1, 2]))]
onnx.save(convert_sklearn(ma_model,initial_types=initial_types,target_opset=12),"AUDJPY D1 MA AI F22 P40.onnx")
Implementierung in MQL5
Wir sind nun bereit, mit der Erstellung unserer Handelsanwendung in MQL5 zu beginnen. Wir wollen eine Handelsanwendung entwickeln, die in der Lage ist, mit Hilfe unserer neu gewonnenen Erkenntnisse über die gleitenden Durchschnitte Positionen einzugehen und zu verlassen. Darüber hinaus werden wir unser Modell im Allgemeinen mit langsameren Indikatoren steuern, die nicht zu aggressive Signale erzeugen. Wir sollten versuchen, nachzubilden, wie menschliche Händler nicht immer eine Position auf dem Markt erzwingen.
Darüber hinaus werden wir auch nachlaufende (trailing) Stop-Loss einsetzen, um ein solides Risikomanagement zu gewährleisten. Wir werden den Indikator Average True Range (ATR) verwenden, um unsere Stop-Loss und Take-Profit dynamisch festzulegen. Unsere Strategie basiert hauptsächlich auf gleitenden Durchschnittskanälen.
Unsere Strategie prognostiziert die gleitenden Durchschnitte 40 Schritte in die Zukunft, um uns eine Bestätigung zu geben, bevor wir eine Position eröffnen können. Wir haben diese Strategie mit historischen Daten aus einem Jahr getestet, die dem Modell während des Trainings nicht angezeigt wurden.
Zunächst importieren wir die ONNX-Datei, die wir gerade erstellt haben.
//+------------------------------------------------------------------+ //| GBPUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load our resources | //+------------------------------------------------------------------+ #resource "\\Files\\AUDJPY D1 MA AI F22 P40.onnx" as const uchar onnx_buffer[]; #resource "\\Files\\AUDJPY D1 RSI AI F22 P40.onnx" as const uchar rsi_onnx_buffer[];
Dann werden wir die benötigten Bibliotheken importieren.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade; #include <Trade\OrderInfo.mqh> class COrderInfo;
Nun werden wir die benötigten globalen Variablen definieren.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; int ma_handler,state; double bid,ask,vol; vectorf model_forecast = vectorf::Zeros(1); vectorf rsi_model_output = vectorf::Zeros(1); double min_volume,max_volume_increase, volume_step, buy_stop_loss, sell_stop_loss,atr_stop,risk_equity; double take_profit = 0; double close_price[3],atr_reading[],ma_buffer[]; long min_distance,login; int atr,close_average,ticket_1,ticket_2; bool authorized = false; double margin,lot_step; string currency,server; bool all_closed =true; int rsi_handler; long rsi_onnx_model; double indicator_reading[]; ENUM_ACCOUNT_TRADE_MODE account_type; const double stop_percent = 1;
Definieren wir unsere Eingangsvariablen.
//+------------------------------------------------------------------+ //| Technical indicators | //+------------------------------------------------------------------+ input group "Money Management" input int lot_multiple = 10; // How big should the lot size be? input double profit_target = 0; // Profit Target input double loss_target = 0; // Max Loss Allowed input group "Money Management" const int atr_period = 200; //ATR Period input double atr_multiple =2.5; //ATR Multiple
Nun müssen wir genau festlegen, wie unsere Handelsanwendung initialisiert werden muss. Wir prüfen zunächst, ob der Nutzer der Anwendung die Erlaubnis zum Handel gegeben hat. Wenn wir die Erlaubnis haben, fortzufahren, werden wir unsere technischen Indikatoren und ONNX-Modelle laden.
int OnInit() { //Authorization if(!TerminalInfoInteger(TERMINAL_TRADE_ALLOWED)) { Comment("Press Ctrl + E To Give The Robot Permission To Trade And Reload The Program"); return(INIT_FAILED); } else if(!MQLInfoInteger(MQL_TRADE_ALLOWED)) { Comment("Reload The Program And Make Sure You Clicked Allow Algo Trading"); return(INIT_FAILED); } else { Comment("This License is Genuine"); setup(); } //Everything was okay return(INIT_SUCCEEDED); }
Wenn unsere Handelsanwendung nicht mehr genutzt wird, müssen wir die nicht mehr benötigten Ressourcen freigeben, um sicherzustellen, dass der Endnutzer unsere Anwendung gut nutzen kann.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { OnnxRelease(onnx_model); OnnxRelease(rsi_onnx_model); IndicatorRelease(atr) }
Sobald wir aktualisierte Kursnotierungen erhalten, werden wir unsere Variablen aktualisieren und nach neuen Handelsmöglichkeiten suchen. Andernfalls, wenn wir bereits offene Handelsgeschäfte haben, sollten wir unseren Trailing-Stop-Loss aktualisieren.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //Update technical data update(); if(PositionsTotal() == 0) { check_setup(); } if(PositionsTotal() > 0) { check_atr_stop(); } }
Um eine Vorhersage von unserem Modell zu erhalten, müssen wir die aktuellen Zustände des RSI und des gleitenden Durchschnittsindikators definieren.
//+------------------------------------------------------------------+ //| Get a prediction from our model | //+------------------------------------------------------------------+ int model_predict(void) { //MA Forecast vectorf model_inputs = vectorf::Zeros(2); vectorf rsi_model_inputs = vectorf::Zeros(3); CopyBuffer(ma_handler,0,0,40,ma_buffer); if(ma_buffer[0] > ma_buffer[39]) { model_inputs[0] = 1; model_inputs[1] = 0; } else if(ma_buffer[0] < ma_buffer[39]) { model_inputs[1] = 1; model_inputs[0] = 0; } //RSI Forecast CopyBuffer(rsi_handler,0,0,1,indicator_reading); if(indicator_reading[0] < 30) { rsi_model_inputs[0] = 1; rsi_model_inputs[1] = 0; rsi_model_inputs[2] = 0; } else if(indicator_reading[0] >70) { rsi_model_inputs[0] = 0; rsi_model_inputs[1] = 1; rsi_model_inputs[2] = 0; } else { rsi_model_inputs[0] = 0; rsi_model_inputs[1] = 0; rsi_model_inputs[2] = 1; } //Model predictions OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); OnnxRun(rsi_onnx_model,ONNX_DEFAULT,rsi_model_inputs,rsi_model_output); //Evaluate model output for buy setup if(((rsi_model_output[0] > 0) && (model_forecast[0] > 0))) { //AI Models forecast Comment("AI Forecast: UP"); return(1); } //Evaluate model output for a sell setup if((rsi_model_output[0] < 0) && (model_forecast[0] < 0)) { Comment("AI Forecast: DOWN"); return(-1); } //Otherwise no position was found return(0); }
Aktualisieren wir unsere globalen Variablen. Für uns ist es einfacher, diese Aktualisierungen in einem Funktionsaufruf durchzuführen, als den gesamten Code direkt im OnTick()-Handler auszuführen.
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update(void) { ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); buy_stop_loss = 0; sell_stop_loss = 0; static datetime time_stamp; datetime time = iTime(_Symbol,PERIOD_CURRENT,0); check_price(3); CopyBuffer(atr,0,0,1,atr_reading); CopyBuffer(ma_handler,0,0,1,ma_buffer); ArraySetAsSeries(atr_reading,true); atr_stop = ((min_volume + atr_reading[0]) * atr_multiple); //On Every Candle if(time_stamp != time) { //Mark the candle time_stamp = time; OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,min_volume,ask,margin); } }
Laden wir die von uns benötigten Ressourcen wie unsere technischen Indikatoren, Konto- und Marktinformationen und andere Daten dieser Art.
//+------------------------------------------------------------------+ //| Load resources | //+------------------------------------------------------------------+ bool setup(void) { //Account Info currency = AccountInfoString(ACCOUNT_CURRENCY); server = AccountInfoString(ACCOUNT_SERVER); login = AccountInfoInteger(ACCOUNT_LOGIN); //Indicators atr = iATR(_Symbol,PERIOD_CURRENT,atr_period); //Setup technical indicators ma_handler =iMA(Symbol(),PERIOD_CURRENT,40,0,MODE_SMA,PRICE_LOW); vol = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,30,PRICE_CLOSE); //Market Information min_volume = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); max_volume_increase = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX) / SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); min_distance = SymbolInfoInteger(_Symbol,SYMBOL_TRADE_STOPS_LEVEL); lot_step = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP); //Define our ONNX model ulong ma_input_shape [] = {1,2}; ulong rsi_input_shape [] = {1,3}; ulong output_shape [] = {1,1}; //Create the model onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); rsi_onnx_model = OnnxCreateFromBuffer(rsi_onnx_buffer,ONNX_DEFAULT); if((onnx_model == INVALID_HANDLE) || (rsi_onnx_model == INVALID_HANDLE)) { Comment("[ERROR] Failed to load AI module correctly"); return(false); } //Validate I/O if((!OnnxSetInputShape(onnx_model,0,ma_input_shape)) || (!OnnxSetInputShape(rsi_onnx_model,0,rsi_input_shape))) { Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()); return(false); } if((!OnnxSetOutputShape(onnx_model,0,output_shape)) || (!OnnxSetOutputShape(rsi_onnx_model,0,output_shape))) { Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()); return(false); } //Everything went fine return(true); }
Alles zusammengenommen sieht unsere Handelsanwendung so aus.
//+------------------------------------------------------------------+ //| GBPUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load our resources | //+------------------------------------------------------------------+ #resource "\\Files\\AUDJPY D1 MA AI F22 P40.onnx" as const uchar onnx_buffer[]; #resource "\\Files\\AUDJPY D1 RSI AI F22 P40.onnx" as const uchar rsi_onnx_buffer[]; //+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade; #include <Trade\OrderInfo.mqh> class COrderInfo; //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; int ma_handler,state; double bid,ask,vol; vectorf model_forecast = vectorf::Zeros(1); vectorf rsi_model_output = vectorf::Zeros(1); double min_volume,max_volume_increase, volume_step, buy_stop_loss, sell_stop_loss,atr_stop,risk_equity; double take_profit = 0; double close_price[3],atr_reading[],ma_buffer[]; long min_distance,login; int atr,close_average,ticket_1,ticket_2; bool authorized = false; double margin,lot_step; string currency,server; bool all_closed =true; int rsi_handler; long rsi_onnx_model; double indicator_reading[]; ENUM_ACCOUNT_TRADE_MODE account_type; const double stop_percent = 1; //+------------------------------------------------------------------+ //| Technical indicators | //+------------------------------------------------------------------+ input group "Money Management" input int lot_multiple = 10; // How big should the lot size be? input double profit_target = 0; // Profit Target input double loss_target = 0; // Max Loss Allowed input group "Money Management" input int bb_period = 36; //Bollinger band period input int ma_period = 4; //Moving average period const int atr_period = 200; //ATR Period input double atr_multiple =2.5; //ATR Multiple //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //Authorization if(!TerminalInfoInteger(TERMINAL_TRADE_ALLOWED)) { Comment("Press Ctrl + E To Give The Robot Permission To Trade And Reload The Program"); return(INIT_FAILED); } else if(!MQLInfoInteger(MQL_TRADE_ALLOWED)) { Comment("Reload The Program And Make Sure You Clicked Allow Algo Trading"); return(INIT_FAILED); } else { Comment("This License is Genuine"); setup(); } //--- Everything was okay return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- OnnxRelease(onnx_model); OnnxRelease(rsi_onnx_model); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update technical data update(); if(PositionsTotal() == 0) { check_setup(); } if(PositionsTotal() > 0) { check_atr_stop(); } } //+------------------------------------------------------------------+ //| Get a prediction from our model | //+------------------------------------------------------------------+ int model_predict(void) { //MA Forecast vectorf model_inputs = vectorf::Zeros(2); vectorf rsi_model_inputs = vectorf::Zeros(3); CopyBuffer(ma_handler,0,0,40,ma_buffer); if(ma_buffer[0] > ma_buffer[39]) { model_inputs[0] = 1; model_inputs[1] = 0; } else if(ma_buffer[0] < ma_buffer[39]) { model_inputs[1] = 1; model_inputs[0] = 0; } //RSI Forecast CopyBuffer(rsi_handler,0,0,1,indicator_reading); if(indicator_reading[0] < 30) { rsi_model_inputs[0] = 1; rsi_model_inputs[1] = 0; rsi_model_inputs[2] = 0; } else if(indicator_reading[0] >70) { rsi_model_inputs[0] = 0; rsi_model_inputs[1] = 1; rsi_model_inputs[2] = 0; } else { rsi_model_inputs[0] = 0; rsi_model_inputs[1] = 0; rsi_model_inputs[2] = 1; } //Model predictions OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); OnnxRun(rsi_onnx_model,ONNX_DEFAULT,rsi_model_inputs,rsi_model_output); //Evaluate model output for buy setup if(((rsi_model_output[0] > 0) && (model_forecast[0] > 0))) { //AI Models forecast Comment("AI Forecast: UP"); return(1); } //Evaluate model output for a sell setup if((rsi_model_output[0] < 0) && (model_forecast[0] < 0)) { Comment("AI Forecast: DOWN"); return(-1); } //Otherwise no position was found return(0); } //+------------------------------------------------------------------+ //| Check for valid trade setups | //+------------------------------------------------------------------+ void check_setup(void) { int res = model_predict(); if(res == -1) { Trade.Sell(vol,Symbol(),bid,0,0,"VD V75 AI"); state = -1; } else if(res == 1) { Trade.Buy(vol,Symbol(),ask,0,0,"VD V75 AI"); state = 1; } } //+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update(void) { ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); buy_stop_loss = 0; sell_stop_loss = 0; static datetime time_stamp; datetime time = iTime(_Symbol,PERIOD_CURRENT,0); check_price(3); CopyBuffer(atr,0,0,1,atr_reading); CopyBuffer(ma_handler,0,0,1,ma_buffer); ArraySetAsSeries(atr_reading,true); atr_stop = ((min_volume + atr_reading[0]) * atr_multiple); //On Every Candle if(time_stamp != time) { //Mark the candle time_stamp = time; OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,min_volume,ask,margin); } } //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| Load resources | //+------------------------------------------------------------------+ bool setup(void) { //Account Info currency = AccountInfoString(ACCOUNT_CURRENCY); server = AccountInfoString(ACCOUNT_SERVER); login = AccountInfoInteger(ACCOUNT_LOGIN); //Indicators atr = iATR(_Symbol,PERIOD_CURRENT,atr_period); //Setup technical indicators ma_handler =iMA(Symbol(),PERIOD_CURRENT,40,0,MODE_SMA,PRICE_LOW); vol = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,30,PRICE_CLOSE); //Market Information min_volume = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); max_volume_increase = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX) / SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); min_distance = SymbolInfoInteger(_Symbol,SYMBOL_TRADE_STOPS_LEVEL); lot_step = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP); //Define our ONNX model ulong ma_input_shape [] = {1,2}; ulong rsi_input_shape [] = {1,3}; ulong output_shape [] = {1,1}; //Create the model onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); rsi_onnx_model = OnnxCreateFromBuffer(rsi_onnx_buffer,ONNX_DEFAULT); if((onnx_model == INVALID_HANDLE) || (rsi_onnx_model == INVALID_HANDLE)) { Comment("[ERROR] Failed to load AI module correctly"); return(false); } //--- Validate I/O if((!OnnxSetInputShape(onnx_model,0,ma_input_shape)) || (!OnnxSetInputShape(rsi_onnx_model,0,rsi_input_shape))) { Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()); return(false); } if((!OnnxSetOutputShape(onnx_model,0,output_shape)) || (!OnnxSetOutputShape(rsi_onnx_model,0,output_shape))) { Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+ //| Close all our open positions | //+------------------------------------------------------------------+ void close_all() { if(PositionsTotal() > 0) { ulong ticket; for(int i =0;i < PositionsTotal();i++) { ticket = PositionGetTicket(i); Trade.PositionClose(ticket); } } } //+------------------------------------------------------------------+ //| Update our trailing ATR stop | //+------------------------------------------------------------------+ void check_atr_stop() { for(int i = PositionsTotal() -1; i >= 0; i--) { string symbol = PositionGetSymbol(i); if(_Symbol == symbol) { ulong ticket = PositionGetInteger(POSITION_TICKET); double position_price = PositionGetDouble(POSITION_PRICE_OPEN); double type = PositionGetInteger(POSITION_TYPE); double current_stop_loss = PositionGetDouble(POSITION_SL); if(type == POSITION_TYPE_BUY) { double atr_stop_loss = (ask - (atr_stop)); double atr_take_profit = (ask + (atr_stop)); if((current_stop_loss < atr_stop_loss) || (current_stop_loss == 0)) { Trade.PositionModify(ticket,atr_stop_loss,atr_take_profit); } } else if(type == POSITION_TYPE_SELL) { double atr_stop_loss = (bid + (atr_stop)); double atr_take_profit = (bid - (atr_stop)); if((current_stop_loss > atr_stop_loss) || (current_stop_loss == 0)) { Trade.PositionModify(ticket,atr_stop_loss,atr_take_profit); } } } } } //+------------------------------------------------------------------+ //| Close our open buy positions | //+------------------------------------------------------------------+ void close_buy() { ulong ticket; int type; if(PositionsTotal() > 0) { for(int i = 0; i < PositionsTotal();i++) { if(PositionGetSymbol(i) == _Symbol) { ticket = PositionGetTicket(i); type = (int)PositionGetInteger(POSITION_TYPE); if(type == POSITION_TYPE_BUY) { Trade.PositionClose(ticket); } } } } } //+------------------------------------------------------------------+ //| Close our open sell positions | //+------------------------------------------------------------------+ void close_sell() { ulong ticket; int type; if(PositionsTotal() > 0) { for(int i = 0; i < PositionsTotal();i++) { if(PositionGetSymbol(i) == _Symbol) { ticket = PositionGetTicket(i); type = (int)PositionGetInteger(POSITION_TYPE); if(type == POSITION_TYPE_SELL) { Trade.PositionClose(ticket); } } } } } //+------------------------------------------------------------------+ //| Get the most recent price values | //+------------------------------------------------------------------+ void check_price(int candles) { for(int i = 0; i < candles;i++) { close_price[i] = iClose(_Symbol,PERIOD_CURRENT,i); } } //+------------------------------------------------------------------+
Testen wir nun unseren Handelsalgorithmus mit Daten, die wir dem Algorithmus beim Training nicht gezeigt haben. Der von uns gewählte Zeitraum erstreckt sich von Anfang Januar 2023 bis zum 28. Juni 2024 auf die täglichen Marktnotierungen des AUDJPY-Paares. Wir setzen den Parameter „Forward“ auf „No“, da wir uns vergewissert haben, dass die von uns ausgewählten Daten beim Training des Modells nicht beobachtet wurden.

Abb. 12: Das Symbol und der Zeitrahmen, die wir zur Bewertung unserer Handelsstrategie verwenden werden.
Darüber hinaus werden wir die realen Handelsbedingungen nachahmen, indem wir den Parameter „Delays“ (Verzögerungen) zunächst auf „Random delay“ (Zufällige Verzögerung) setzen. Dieser Parameter steuert die Latenzzeit zwischen dem Zeitpunkt, an dem unsere Aufträge erteilt werden, und dem Zeitpunkt ihrer Ausführung. Die Einstellung zufällig entspricht dem realen Handelsgeschehen, denn die Latenzzeit ist nicht immer konstant. Außerdem werden wir unser Terminal anweisen, den Markt mit echten Ticks zu modellieren. Diese Einstellung wird unseren Backtest etwas verlangsamen, da das Terminal zunächst detaillierte Marktdaten von unserem Broker über das Internet abrufen muss.
Die letzten Parameter, die die Kontoeinlage und die Hebelwirkung steuern, sollten an Ihre Handelseinstellungen angepasst werden. Wenn wir alle angeforderten Daten erfolgreich abgerufen haben, beginnt unser Backtest.
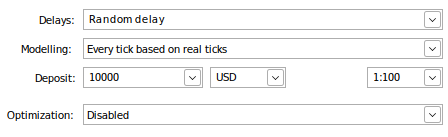
Abb. 13: Die Parameter, die wir für unseren Rückentest verwenden werden.
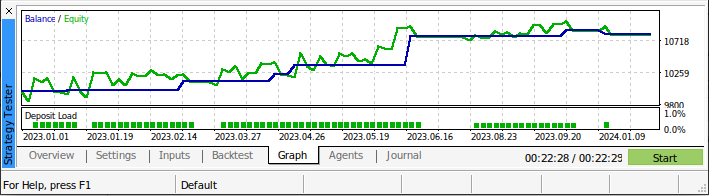
Abb. 14: Die Leistung unserer Strategie bei Daten, für die unser Modell nicht trainiert wurde.
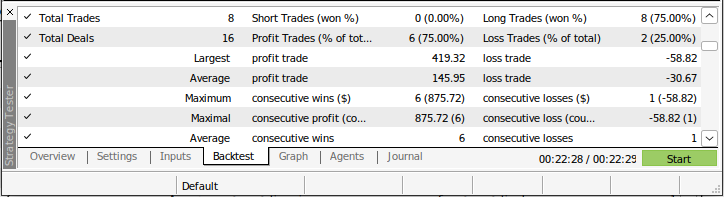
Abb. 12: Weitere Einzelheiten zu unserem Backtest mit ungesehenen Marktdaten.
Schlussfolgerung
Die breiten Marktdaten, die wir heute analysiert haben, zeigen uns deutlich, dass man, wenn man Intervalle von weniger als 40 Schritten in die Zukunft vorhersagen will, wahrscheinlich besser daran tut, die Preise direkt vorherzusagen. Wenn Sie jedoch mehr als 40 Schritte in die Zukunft prognostizieren wollen, ist es wahrscheinlich besser, die Veränderung des gleitenden Durchschnitts vorherzusagen, als die Veränderung des Preises. Es gibt immer mehr Verbesserungen, die darauf warten, dass wir sie und den Unterschied, den sie machen, beobachten. Es ist klar zu erkennen, dass sich jeder Zeitaufwand für die Umwandlung der Dateneingaben lohnt, da wir so die zugrunde liegenden Beziehungen zu unseren Modellen auf sinnvollere Weise aufdecken können.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/16230
 Erforschung der Kryptographie in MQL5: Ein Schritt-für-Schritt-Ansatz
Erforschung der Kryptographie in MQL5: Ein Schritt-für-Schritt-Ansatz
 Handel mit dem MQL5 Wirtschaftskalender (Teil 1): Beherrschung der Funktionen des MQL5-Wirtschaftskalenders
Handel mit dem MQL5 Wirtschaftskalender (Teil 1): Beherrschung der Funktionen des MQL5-Wirtschaftskalenders
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 45): Reinforcement Learning mit Monte-Carlo
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 45): Reinforcement Learning mit Monte-Carlo
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 44): Technischer Indikator Average True Range (ATR)
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 44): Technischer Indikator Average True Range (ATR)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.