Monte Carlo Permutationstests im MetaTrader 5

Einführung

Aleksey Nikolayev, schrieb einen interessanten Artikel mit dem Titel „Mit der Monte-Carlo-Methode Handelsstrategien optimieren“. Er beschreibt eine Methode der Permutationsprüfung, bei der eine Folge von Handelsgeschäften aus einem Test zufällig umgewandelt wird. Der Autor erwähnt kurz eine andere Art von Permutationstest, bei dem die Reihenfolge der Preisdaten zufällig geändert wird und die Leistung eines einzelnen Expert Advisors (EA) mit der Leistung verglichen wird, die bei zahlreichen anderen Variationen der Reihenfolge derselben Preisreihe erzielt wurde.

Meiner Meinung nach hat der Autor fälschlicherweise behauptet, dass es keine Möglichkeit gäbe, einen solchen Test mit einem beliebigen EA in MetaTrader 5 durchzuführen. Zumindest nicht vollständig. Daher werden wir in diesem Artikel einen Permutationstest mit zufällig permutierten Kursdaten unter Verwendung von MetaTrader 5 demonstrieren. Wir werden Code für die Permutation von Preisreihen sowie ein Skript vorstellen, das die ersten Schritte bei der Vorbereitung eines Permutationstests für einen kompletten EA automatisiert.

Überblick über Permutationstests

Um es kurz zu machen: Bei dem hier beschriebenen Permutationstest wird eine Stichprobe von Preisdaten ausgewählt. Es ist vorzuziehen, dass der Test außerhalb der Probe durchgeführt wird. Nachdem wir einen Test mit dieser Preisreihe durchgeführt haben, notieren wir uns die Leistungskriterien, die wir messen möchten. Dann ändern wir zufällig die Reihenfolge der ursprünglichen Preisreihen, testen den EA und notieren die Leistung.

Wir führen dies mehrmals durch, wobei wir jedes Mal die Preisreihen permutieren und die daraus resultierenden Leistungskriterien aufzeichnen, die wir bei anderen Tests festgestellt haben. Dies sollte mindestens hundertmal, idealerweise tausendmal, geschehen. Je öfter wir permutieren und testen, desto robuster werden die Ergebnisse sein. Aber, Moment mal, was sollen unsere Ergebnisse über den getesteten EA aussagen?

Wert der Durchführung von Permutationstests

Wenn eine Reihe von iterativen Tests durchgeführt wurde, erhalten wir eine Sammlung von Leistungsdaten aus jeder Permutation. Dabei spielt es keine Rolle, welche Performance-Kennzahl wir verwenden, es kann die Sharpe Ratio, der Profitfaktor oder einfach der resultierende Saldo oder Nettogewinn sein. Angenommen, es wurden 99 Permutationen durchgeführt, einschließlich der 100 Permutationen des ursprünglichen unveränderten Tests. Wir haben 100 Leistungszahlen zum Vergleich.

Der nächste Schritt besteht darin, die Anzahl der Überschreitungen des Leistungswerts für den nicht permutierten Test aufzuzählen und diese Anzahl als Bruchteil der durchgeführten Tests, in diesem Fall 100, darzustellen. Dieser Bruchteil ist die Wahrscheinlichkeit, zufällig das Ergebnis des unverfälschten Tests oder besser zu erhalten, wenn der EA überhaupt kein Gewinnpotenzial hätte. In der Statistik wird er als p-Wert bezeichnet und ist das Ergebnis eines Hypothesentests.

Wenn wir unseren hypothetischen Permutationstest mit 100 Iterationen fortsetzen, ergibt sich, dass genau 29 permutierte Leistungswerte besser sind als der nicht-permutierte Benchmark-Test. Wir erhalten einen p-Wert von 0,3, d. h. (29+1)/100. Das bedeutet, dass eine Wahrscheinlichkeit von 0,3 besteht, dass ein EA, der Geld verliert, eine ähnliche oder bessere Leistung erzielt hätte, wie sie bei dem nicht permutierten Test beobachtet wurde. Ein solches Ergebnis mag ermutigend erscheinen, aber was wir wollen, sind p-Werte, die so nahe wie möglich bei Null liegen, etwa im Bereich von 0,05 und darunter.

Die vollständige Formel ist unten angegeben:

z+1/r+1

Dabei ist r die Anzahl der durchgeführten Permutationen und z die Gesamtzahl der permutierten Tests mit besserer Leistung. Um den Test richtig durchzuführen, ist das Permutationsverfahren wichtig.

Permutation von Preisreihen

Um eine Datensammlung korrekt zu permutieren, müssen wir sicherstellen, dass jede mögliche Sequenzvariation gleich wahrscheinlich ist. Dazu muss eine gleichmäßig verteilte Zufallszahl zwischen 0 und 1 erzeugt werden. Die mql5-Standardbibliothek bietet in der Statistik-Bibliothek ein Werkzeug, das diese Aufgabe erledigt. Damit können wir den Bereich der geforderten Werte festlegen.

//+------------------------------------------------------------------+
//| Random variate from the Uniform distribution                     |
//+------------------------------------------------------------------+
//| Computes the random variable from the Uniform distribution       |
//| with parameters a and b.                                         |
//|                                                                  |
//| Arguments:                                                       |
//| a           : Lower endpoint (minimum)                           |
//| b           : Upper endpoint (maximum)                           |
//| error_code  : Variable for error code                            |
//|                                                                  |
//| Return value:                                                    |
//| The random value with uniform distribution.                      |
//+------------------------------------------------------------------+
double MathRandomUniform(const double a,const double b,int &error_code)
  {
//--- check NaN
   if(!MathIsValidNumber(a) || !MathIsValidNumber(b))
     {
      error_code=ERR_ARGUMENTS_NAN;
      return QNaN;
     }
//--- check upper bound
   if(b<a)
     {
      error_code=ERR_ARGUMENTS_INVALID;
      return QNaN;
     }

   error_code=ERR_OK;
//--- check ranges
   if(a==b)
      return a;
//---
   return a+MathRandomNonZero()*(b-a);
  }

Die Umstellung von Preisdaten stellt besondere Anforderungen. Erstens können wir nicht einfach die Position eines Preiswerts ändern, da dies die für Finanzzeitreihen charakteristischen zeitlichen Beziehungen stören würde. Anstelle der tatsächlichen Preise werden wir also Preisänderungen permutieren. Indem wir die Preise zunächst logarithmisch transformieren, bevor wir sie differenzieren, minimieren wir den Einfluss von Schwankungen bei den Rohpreisunterschieden.

Bei dieser Methode müssen wir den ersten Preiswert zurückhalten und ihn aus der Permutation ausschließen. Wenn die Reihe rekonstruiert wird, bleibt der in der ursprünglichen Preisfolge vorhandene Trend erhalten. Die einzige Abweichung sind die internen Preisbewegungen zwischen demselben ersten und letzten Preis der ursprünglichen Serie.

Vor der eigentlichen Umrechnung der Preisreihen müssen wir entscheiden, welche Daten wir verwenden wollen. In MetaTrader 5 werden die Diagrammdaten als Balken angezeigt, die aus Tickdaten aufgebaut sind. Das Permutieren einer einzelnen Preisreihe ist viel einfacher als das Permutieren von Balkeninformationen. Wir werden also Tickdaten verwenden. Die Verwendung von Ticks bringt auch eine Reihe anderer Komplikationen mit sich, da Ticks neben den Rohpreisen auch andere Informationen enthalten. Es gibt Informationen über Volumen, Zeit und Tick-Flags.

Erstens bleiben die Zeit- und Tick-Flag-Informationen unangetastet, sodass unsere Permutationsroutine diese Informationen nicht verändern sollte. Wir interessieren uns nur für das Angebot, die Nachfrage und das Volumen. Die zweite Komplikation ergibt sich aus der Möglichkeit, dass einer dieser Werte gleich Null sein kann, was bei der Anwendung einer Log-Transformation auf diese Werte zu Problemen führt. Um zu demonstrieren, wie man diese Herausforderungen meistert, schauen wir uns etwas Code an.

Implementierung des Permutationsalgorithmus der Ticks

Die Klasse CPermuteTicks, die in der Include-Datei PermuteTicks.mqh enthalten ist, implementiert unser Verfahren zur Permutation von Ticks. In PermuteTicks.mqh binden wir Uniform.mqh aus der Standardbibliothek ein, um Zugang zu einem Dienstprogramm zu erhalten, das gleichmäßig generierte Zufallszahlen innerhalb eines bestimmten Bereichs ausgibt. Die folgenden Definitionen legen diesen Bereich fest. Wenn Sie diese Werte ändern möchten, achten Sie darauf, dass das Minimum tatsächlich unter dem Maximum liegt.

//+------------------------------------------------------------------+
//|                                                 PermuteTicks.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Uniform.mqh>
//+-----------------------------------------------------------------------------------+
//| defines: representing range of random values from random number generator         |
//+-----------------------------------------------------------------------------------+
#define MIN_THRESHOLD 1e-5
#define MAX_THRESHOLD 1.0

Die CMqlTick-Struktur repräsentiert die entsprechenden Mitglieder der eingebauten MqlTick-Struktur, die von der Klasse bearbeitet wird. Andere Informationen der Ticks werden nicht berührt.

//+------------------------------------------------------------------+
//| struct to handle tick data to be worked on                       |
//+------------------------------------------------------------------+
struct CMqlTick
  {
   double            ask_d;
   double            bid_d;
   double            vol_d;
   double            volreal_d;
  };

Die Klasse CPermuteTicks hat 3 private Array-Eigenschaften, die Folgendes speichern: erstens die ursprünglichen Ticks, die in m_ticks gespeichert sind, zweitens die logarithmisch transformierten Ticks, die in m_logticks gespeichert sind, und drittens die differenzierten Ticks, die in m_differenced gespeichert sind.

//+------------------------------------------------------------------+
//| Class to enable permutation of a collection of ticks in an array |
//+------------------------------------------------------------------+
class CPermuteTicks
  {
private :
   MqlTick           m_ticks[];        //original tick data to be shuffled
   CMqlTick          m_logticks[];     //log transformed tick data of original ticks
   CMqlTick          m_differenced[];  //log difference of tick data
   bool              m_initialized;    //flag representing proper preparation of a dataset
   //helper methods
   bool              LogTransformTicks(void);
   bool              ExpTransformTicks(MqlTick &out_ticks[]);

public :
   //constructor
                     CPermuteTicks(void);
   //desctrucotr
                    ~CPermuteTicks(void);
   bool              Initialize(MqlTick &in_ticks[]);
   bool              Permute(MqlTick &out_ticks[]);
  };

m_initialized ist ein boolesches Flag, das einen erfolgreichen Vorverarbeitungsvorgang signalisiert, bevor Permutationen durchgeführt werden können.

Um die Klasse zu verwenden, müsste ein Nutzer die Methode Initialize() aufrufen, nachdem er eine Instanz des Objekts erstellt hat. Die Methode erfordert ein Array von Ticks, das permutiert werden sollen. Innerhalb der Methode werden unzugängliche Klassenarrays in ihrer Größe verändert und LogTranformTicks() wird zur Transformation der Tick-Daten herangezogen. Dabei wird darauf geachtet, dass Nullen oder negative Werte vermieden und durch 1,0 ersetzt werden. Nach erfolgter Permutation und Protokolltransformation werden die Tickdaten mit der privaten Methode ExpTransformTicks() in ihren ursprünglichen Bereich zurückgeführt.

//+--------------------------------------------------------------------+
//|Initialize the permutation process by supplying ticks to be permuted|
//+--------------------------------------------------------------------+
bool CPermuteTicks::Initialize(MqlTick &in_ticks[])
  {
//---set or reset initialization flag  
   m_initialized=false;
//---check arraysize
   if(in_ticks.Size()<5)
     {
      Print("Insufficient amount of data supplied ");
      return false;
     }
//---copy ticks to local array
   if(ArrayCopy(m_ticks,in_ticks)!=int(in_ticks.Size()))
     {
      Print("Error copying ticks ", GetLastError());
      return false;
     }
//---ensure the size of m_differenced array
   if(m_differenced.Size()!=m_ticks.Size()-1)
      ArrayResize(m_differenced,m_ticks.Size()-1);
//---apply log transformation to relevant tick data members
   if(!LogTransformTicks())
     {
      Print("Log transformation failed ", GetLastError());
      return false;
     }
//---fill m_differenced with differenced values, excluding the first tick
   for(uint i=1; i<m_logticks.Size(); i++)
     {
      m_differenced[i-1].bid_d=(m_logticks[i].bid_d)-(m_logticks[i-1].bid_d);
      m_differenced[i-1].ask_d=(m_logticks[i].ask_d)-(m_logticks[i-1].ask_d);
      m_differenced[i-1].vol_d=(m_logticks[i].vol_d)-(m_logticks[i-1].vol_d);
      m_differenced[i-1].volreal_d=(m_logticks[i].volreal_d)-(m_logticks[i-1].volreal_d);
     }
//---set the initilization flag
   m_initialized=true;
//---
   return true;
  }

Um permutierte Ticks auszugeben, sollte die treffend benannte Methode Permute() aufgerufen werden. Sie benötigt nur einen einzigen Parameter, nämlich ein dynamisches MqlTick-Array, in dem die permutierten Ticks abgelegt werden. Hier befindet sich die Tick-Shuffling-Prozedur innerhalb einer while-Schleife, die die Position eines differenzierten Tick-Wertes in Abhängigkeit von der bei jeder Iteration erzeugten Zufallszahl vertauscht.

//+------------------------------------------------------------------+
//|Public method which applies permutation and gets permuted ticks   |
//+------------------------------------------------------------------+
bool CPermuteTicks::Permute(MqlTick &out_ticks[])
  {
//---zero out tick array  
   ZeroMemory(out_ticks);
//---ensure required data already supplied through initialization
   if(!m_initialized)
     {
      Print("not initialized");
      return false;
     }
//---resize output array if necessary
   if(out_ticks.Size()!=m_ticks.Size())
      ArrayResize(out_ticks,m_ticks.Size());
//---
   int i,j;
   CMqlTick tempvalue;

   i=(int)m_ticks.Size()-1;
   
   int error_value;
   double unif_rando;

   ulong time = GetTickCount64();

   while(i>1)
     {
      error_value=0;
      unif_rando=MathRandomUniform(MIN_THRESHOLD,MAX_THRESHOLD,error_value);
      if(!MathIsValidNumber(unif_rando))
        {
         Print("Invalid random value ",error_value);
         return(false);
        }
      j=(int)(unif_rando*i);
      if(j>=i)
         j=i-1;
      --i;
//---swap tick data randomly
      tempvalue.bid_d=m_differenced[i].bid_d;
      tempvalue.ask_d=m_differenced[i].ask_d;
      tempvalue.vol_d=m_differenced[i].vol_d;
      tempvalue.volreal_d=m_differenced[i].volreal_d;

      m_differenced[i].bid_d=m_differenced[j].bid_d;
      m_differenced[i].ask_d=m_differenced[j].ask_d;
      m_differenced[i].vol_d=m_differenced[j].vol_d;
      m_differenced[i].volreal_d=m_differenced[j].volreal_d;

      m_differenced[j].bid_d=tempvalue.bid_d;
      m_differenced[j].ask_d=tempvalue.ask_d;
      m_differenced[j].vol_d=tempvalue.vol_d;
      m_differenced[j].volreal_d=tempvalue.volreal_d;
     }
//---undo differencing 
   for(uint k = 1; k<m_ticks.Size(); k++)
     {
      m_logticks[k].bid_d=m_logticks[k-1].bid_d + m_differenced[k-1].bid_d;
      m_logticks[k].ask_d=m_logticks[k-1].ask_d + m_differenced[k-1].ask_d;
      m_logticks[k].vol_d=m_logticks[k-1].vol_d + m_differenced[k-1].vol_d;
      m_logticks[k].volreal_d=m_logticks[k-1].volreal_d + m_differenced[k-1].volreal_d;
     }
//---copy the first tick  
   out_ticks[0].bid=m_ticks[0].bid;
   out_ticks[0].ask=m_ticks[0].ask;
   out_ticks[0].volume=m_ticks[0].volume;
   out_ticks[0].volume_real=m_ticks[0].volume_real;
   out_ticks[0].flags=m_ticks[0].flags;
   out_ticks[0].last=m_ticks[0].last;
   out_ticks[0].time=m_ticks[0].time;
   out_ticks[0].time_msc=m_ticks[0].time_msc;     
//---return transformed data
   return ExpTransformTicks(out_ticks);
  }
//+------------------------------------------------------------------+

Nach Abschluss aller Iterationen wird das Array m_logticks neu aufgebaut, indem die Differenzierung unter Verwendung der permutierten m_differenzierten Tick-Daten rückgängig gemacht wird. Schließlich wird das einzige Argument der Methode Permute() mit m_logtick-Daten gefüllt, die in den ursprünglichen Bereich zurückgegeben werden, wobei die Zeit- und Tick-Flag-Informationen aus der ursprünglichen Tick-Serie kopiert werden.

//+-------------------------------------------------------------------+
//|Helper method applying log transformation                          |
//+-------------------------------------------------------------------+
bool CPermuteTicks::LogTransformTicks(void)
  {
//---resize m_logticks if necessary  
   if(m_logticks.Size()!=m_ticks.Size())
      ArrayResize(m_logticks,m_ticks.Size());
//---log transform only relevant data members, avoid negative and zero values
   for(uint i=0; i<m_ticks.Size(); i++)
     {
      m_logticks[i].bid_d=(m_ticks[i].bid>0)?MathLog(m_ticks[i].bid):MathLog(1e0);
      m_logticks[i].ask_d=(m_ticks[i].ask>0)?MathLog(m_ticks[i].ask):MathLog(1e0);
      m_logticks[i].vol_d=(m_ticks[i].volume>0)?MathLog(m_ticks[i].volume):MathLog(1e0);
      m_logticks[i].volreal_d=(m_ticks[i].volume_real>0)?MathLog(m_ticks[i].volume_real):MathLog(1e0);
     }
//---
   return true;
  }

//+-----------------------------------------------------------------------+
//|Helper method undoes log transformation before outputting permuted tick|
//+-----------------------------------------------------------------------+
bool CPermuteTicks::ExpTransformTicks(MqlTick &out_ticks[])
  {
//---apply exponential transform to data and copy original tick data member info
//---not involved in permutation operations
   for(uint k = 1; k<m_ticks.Size(); k++)
     {
      out_ticks[k].bid=(m_logticks[k].bid_d)?MathExp(m_logticks[k].bid_d):0;
      out_ticks[k].ask=(m_logticks[k].ask_d)?MathExp(m_logticks[k].ask_d):0;
      out_ticks[k].volume=(m_logticks[k].vol_d)?(ulong)MathExp(m_logticks[k].vol_d):0;
      out_ticks[k].volume_real=(m_logticks[k].volreal_d)?MathExp(m_logticks[k].volreal_d):0;
      out_ticks[k].flags=m_ticks[k].flags;
      out_ticks[k].last=m_ticks[k].last;
      out_ticks[k].time=m_ticks[k].time;
      out_ticks[k].time_msc=m_ticks[k].time_msc;
     }
//---
   return true;
  }

Wir haben jetzt einen Algorithmus, der mit den Permutationen der Preisreihen umgehen kann, aber das ist nur die halbe Miete, wir müssen noch den Test machen.

Verfahren des Permutationstests

Das Verfahren des Permutationstests nutzt zwei Funktionen des MetaTrader 5 Terminals. Die erste ist die Möglichkeit, nutzerdefinierte Symbole zu erstellen und deren Eigenschaften festzulegen. Die zweite ist die Möglichkeit, EA's entsprechend der aktivierten Symbole in der Market Watch List zu optimieren. Es gibt also noch mindestens zwei weitere Schritte in diesem Prozess.

Wir können die Ticks permutieren und nutzerdefinierte Symbole erstellen. Wenn wir dies zusammennehmen, können wir nutzerdefinierte Symbole auf der Grundlage eines beliebigen vorhandenen Symbols erstellen. Jedes nutzerdefinierte Symbol wird mit einer eindeutigen Permutation der Ticks für das als Basis verwendete Symbol angegeben. Die Erstellung von Symbolen kann manuell erfolgen, aber warum sollten wir uns selbst bestrafen, wenn wir die gesamte Aufgabe der Symbolerstellung und des Hinzufügens permutierter Ticks automatisieren könnten.

Das Skript PrepareSymbolsForPermutationTests tut genau dies. Seine nutzerspezifischen Eingaben ermöglichen die Festlegung eines Basissymbols, des Datumsbereichs der in den Permutationen zu verwendenden Ticks vom Basissymbol, der Anzahl der erforderlichen Permutationen, die der Anzahl der zu erstellenden nutzerdefinierten Symbole entspricht, und eines optionalen String-Identifikators, der an die Namen der neuen nutzerdefinierten Symbole angehängt wird.

//+------------------------------------------------------------------+
//|                            PrepareSymbolsForPermutationTests.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<GenerateSymbols.mqh>
#property script_show_inputs
//--- input parameters
input string   BaseSymbol="EURUSD";
input datetime StartDate=D'2023.06.01 00:00';
input datetime EndDate=D'2023.08.01 00:00';
input uint     Permutations=100;
input string   CustomID="";//SymID to be added to symbol permutation names
//---
CGenerateSymbols generateSymbols();
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   if(!generateSymbols.Initiate(BaseSymbol,CustomID,StartDate,EndDate))
       return;
//---
   Print("Number of newly generated symbols is ", generateSymbols.Generate(Permutations));
//---          
  }
//+------------------------------------------------------------------+

Das Skript erstellt automatisch Symbolnamen unter Verwendung des Basissymbolnamens, mit einer Aufzählung am Ende. Der Code, der all dies bewirkt, ist in GenerateSymbols.mqh enthalten, das die Definition der Klasse CGenerateSymbols enthält. Die Klassendefinition stützt sich auf zwei weitere Abhängigkeiten: NewSymbol.mqh, die die Definition der Klasse CNewSymbol enthält, die aus dem Artikel „MQL5 Cookbook: Stresstests für Handelsstrategien mit nutzerdefinierten Symbolen“.

//+------------------------------------------------------------------+
//| Class CNewSymbol.                                                |
//| Purpose: Base class for a custom symbol.                         |
//+------------------------------------------------------------------+
class CNewSymbol : public CObject
  {
   //--- === Data members === ---
private:
   string            m_name;
   string            m_path;
   MqlTick           m_tick;
   ulong             m_from_msc;
   ulong             m_to_msc;
   uint              m_batch_size;
   bool              m_is_selected;
   //--- === Methods === ---
public:
   //--- constructor/destructor
   void              CNewSymbol(void);
   void             ~CNewSymbol(void) {};
   //--- create/delete
   int               Create(const string _name,const string _path="",const string _origin_name=NULL,
                            const uint _batch_size=1e6,const bool _is_selected=false);
   bool              Delete(void);
   //--- methods of access to protected data
   string            Name(void) const { return(m_name); }
   bool              RefreshRates(void);
   //--- fast access methods to the integer symbol properties
   bool              Select(void) const;
   bool              Select(const bool select);
   //--- service methods
   bool              Clone(const string _origin_symbol,const ulong _from_msc=0,const ulong _to_msc=0);
   bool              LoadTicks(const string _src_file_name);
   //--- API
   bool              SetProperty(ENUM_SYMBOL_INFO_DOUBLE _property,double _val) const;
   bool              SetProperty(ENUM_SYMBOL_INFO_INTEGER _property,long _val) const;
   bool              SetProperty(ENUM_SYMBOL_INFO_STRING _property,string _val) const;
   double            GetProperty(ENUM_SYMBOL_INFO_DOUBLE _property) const;
   long              GetProperty(ENUM_SYMBOL_INFO_INTEGER _property) const;
   string            GetProperty(ENUM_SYMBOL_INFO_STRING _property) const;
   bool              SetSessionQuote(const ENUM_DAY_OF_WEEK _day_of_week,const uint _session_index,
                                     const datetime _from,const datetime _to);
   bool              SetSessionTrade(const ENUM_DAY_OF_WEEK _day_of_week,const uint _session_index,
                                     const datetime _from,const datetime _to);
   int               RatesDelete(const datetime _from,const datetime _to);
   int               RatesReplace(const datetime _from,const datetime _to,const MqlRates &_rates[]);
   int               RatesUpdate(const MqlRates &_rates[]) const;
   int               TicksAdd(const MqlTick &_ticks[]) const;
   int               TicksDelete(const long _from_msc,long _to_msc) const;
   int               TicksReplace(const MqlTick &_ticks[]) const;
   //---
private:
   template<typename PT>
   bool              CloneProperty(const string _origin_symbol,const PT _prop_type) const;
   int               CloneTicks(const MqlTick &_ticks[]) const;
   int               CloneTicks(const string _origin_symbol) const;
  };

Die Klasse hilft bei der Erstellung neuer nutzerdefinierter Symbole auf der Grundlage vorhandener Symbole. Die letzte erforderliche Abhängigkeit ist die von PermuteTicks.mqh, auf die wir bereits gestoßen sind.

//+------------------------------------------------------------------+
//|                                              GenerateSymbols.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<PermuteTicks.mqh>
#include<NewSymbol.mqh>
//+------------------------------------------------------------------+
//| defines:max number of ticks download attempts and array resize   |
//+------------------------------------------------------------------+
#define MAX_DOWNLOAD_ATTEMPTS 10 
#define RESIZE_RESERVE 100
//+------------------------------------------------------------------+
//|CGenerateSymbols class                                            |
//| creates custom symbols from an existing base symbol's tick data  |
//|  symbols represent permutations of base symbol's ticks           |
//+------------------------------------------------------------------+
class CGenerateSymbols
{
 private:
   string         m_basesymbol;     //base symbol
   string         m_symbols_id;     //common identifier added to names of new symbols 
   long           m_tickrangestart; //beginning date for range of base symbol's ticks
   long           m_tickrangestop;  //ending date for range of base symbol's ticks
   uint           m_permutations;   //number of permutations and ultimately the number of new symbols to create
   MqlTick        m_baseticks[];    //base symbol's ticks
   MqlTick        m_permutedticks[];//permuted ticks;
   CNewSymbol    *m_csymbols[];     //array of created symbols
   CPermuteTicks *m_shuffler;       //object used to shuffle tick data
   
 public: 
   CGenerateSymbols(void);
   ~CGenerateSymbols(void);                      
   bool Initiate(const string base_symbol,const string symbols_id,const datetime start_date,const datetime stop_date);
   uint Generate(const uint permutations);
};

CGenerateSymbols hat zwei Mitgliedsfunktionen, die ein Nutzer kennen muss. Die Methode Initiate() sollte zuerst nach der Objekterstellung aufgerufen werden. Sie hat 4 Parameter, die den Nutzereingaben des bereits erwähnten Skripts entsprechen.

//+-----------------------------------------------------------------------------------------+
//|set and check parameters for symbol creation, download ticks and initialize tick shuffler|
//+-----------------------------------------------------------------------------------------+
bool CGenerateSymbols::Initiate(const string base_symbol,const string symbols_id,const datetime start_date,const datetime stop_date)
{
//---reset number of permutations previously done
 m_permutations=0;
//---set base symbol
 m_basesymbol=base_symbol;
//---make sure base symbol is selected, ie, visible in WatchList 
 if(!SymbolSelect(m_basesymbol,true))
  {
   Print("Failed to select ", m_basesymbol," error ", GetLastError());
   return false;
  }
//---set symbols id 
 m_symbols_id=symbols_id;
//---check, set ticks date range
 if(start_date>=stop_date)
   {
    Print("Invalid date range ");
    return false;
   }
 else
   {
    m_tickrangestart=long(start_date)*1000;
    m_tickrangestop=long(stop_date)*1000;
   }  
//---check shuffler object
   if(CheckPointer(m_shuffler)==POINTER_INVALID)
    {
     Print("CPermuteTicks object creation failed");
     return false;
    }
//---download ticks
   Comment("Downloading ticks");
   uint attempts=0;
   int downloaded=-1;
    while(attempts<MAX_DOWNLOAD_ATTEMPTS)
     {
      downloaded=CopyTicksRange(m_basesymbol,m_baseticks,COPY_TICKS_ALL,m_tickrangestart,m_tickrangestop);
      if(downloaded<=0)
        {
         Sleep(500);
         ++attempts;
        }
      else 
        break;   
     }
//---check download result
   if(downloaded<=0)
    {
     Print("Failed to get tick data for ",m_basesymbol," error ", GetLastError());
     return false;
    }          
  Comment("Ticks downloaded");  
//---return shuffler initialization result   
  return m_shuffler.Initialize(m_baseticks);        
}                      

Die Methode Generate() nimmt als Eingabe die gewünschte Anzahl von Permutationen und gibt die Anzahl der neuen nutzerdefinierten Symbole zurück, die dem Marchet Watch des Terminals hinzugefügt wurden.
Das Ergebnis der Ausführung des Skripts wird auf der Registerkarte „Experte“ im Terminal angezeigt.

//+------------------------------------------------------------------+
//| generate symbols return newly created or refreshed symbols       |
//+------------------------------------------------------------------+
uint CGenerateSymbols::Generate(const uint permutations)
{
//---check permutations
 if(!permutations)
   {
    Print("Invalid parameter value for Permutations ");
    return 0;
   } 
//---resize m_csymbols
  if(m_csymbols.Size()!=m_permutations+permutations)
    ArrayResize(m_csymbols,m_permutations+permutations,RESIZE_RESERVE);
//---
  string symspath=m_basesymbol+m_symbols_id+"_PermutedTicks"; 
  int exists;
//---do more permutations
  for(uint i=m_permutations; i<m_csymbols.Size(); i++)
      {
       if(CheckPointer(m_csymbols[i])==POINTER_INVALID)
              m_csymbols[i]=new CNewSymbol();
       exists=m_csymbols[i].Create(m_basesymbol+m_symbols_id+"_"+string(i+1),symspath,m_basesymbol); 
       if(exists>0)
          {
           Comment("new symbol created "+m_basesymbol+m_symbols_id+"_"+string(i+1) );
            if(!m_csymbols[i].Clone(m_basesymbol) || !m_shuffler.Permute(m_permutedticks))
                 break;
            else
                {
                 m_csymbols[i].Select(true);
                 Comment("adding permuted ticks");
                 if(m_csymbols[i].TicksAdd(m_permutedticks)>0)
                      m_permutations++;
                }              
          }
       else
          {
           Comment("symbol exists "+m_basesymbol+m_symbols_id+"_"+string(i+1) );
           m_csymbols[i].Select(true);
           if(!m_shuffler.Permute(m_permutedticks))
                 break;
           Comment("replacing ticks ");
           if(m_csymbols[i].TicksReplace(m_permutedticks)>0)
              m_permutations++;
           else
              break;   
          } 
     }   
//---return successful number of permutated symbols
 Comment("");
//--- 
 return m_permutations;
}

Der nächste Schritt besteht darin, die Optimierung im Strategietester auszuführen. Stellen Sie sicher, dass Sie die letzte Optimierungsmethode auswählen und den zu testenden EA angeben. Starten Sie den Test und suchen Sie sich eine Beschäftigung für eine Weile, da dies wahrscheinlich sehr lange dauern wird. Wenn der Strategietester fertig ist, haben wir eine Sammlung von Leistungsdaten, auf die wir zurückgreifen können.

Ein Beispiel

Lassen Sie uns einen Blick darauf werfen, wie all dies aussieht, indem wir einen Test mit dem mitgelieferten MACD Sample EA durchführen. Der Test wird für das AUDUSD-Symbol mit 100 im Skript festgelegten Permutationen durchgeführt.

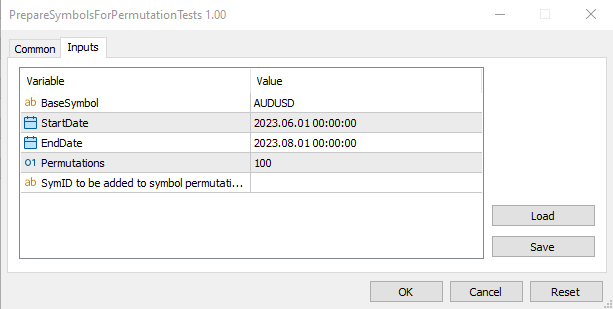
Nach der Ausführung des Skripts haben wir unsere 100 zusätzlichen Symbole, die auf den permutierten Ticks einer Stichprobe des ausgewählten AUDUSD-Symbols basieren.

Schließlich führen wir den Optimierungstest durch.

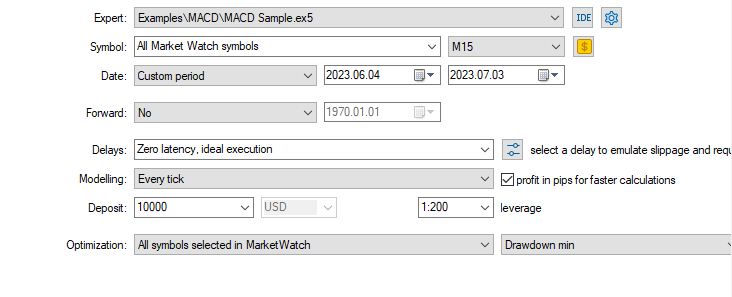
  Die verwendeten EA-Einstellungen sind unten aufgeführt.

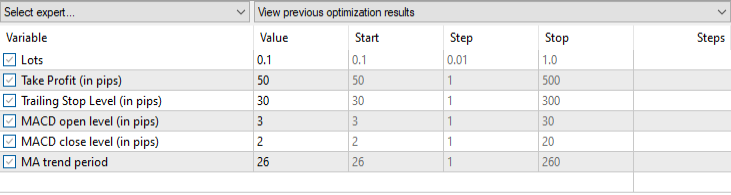
Die Ergebnisse des Tests.

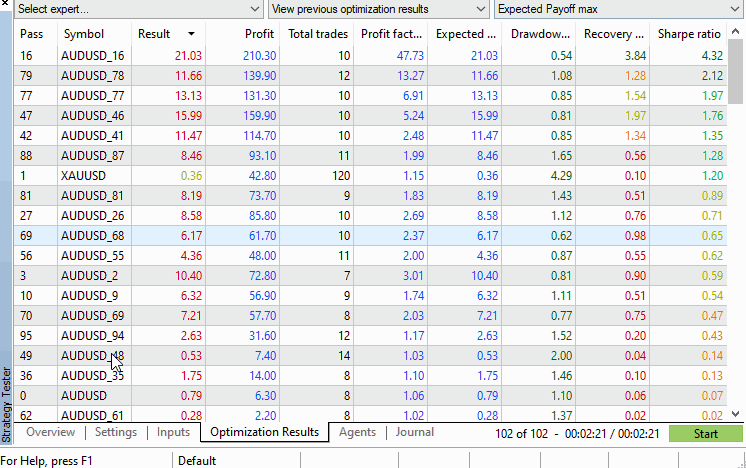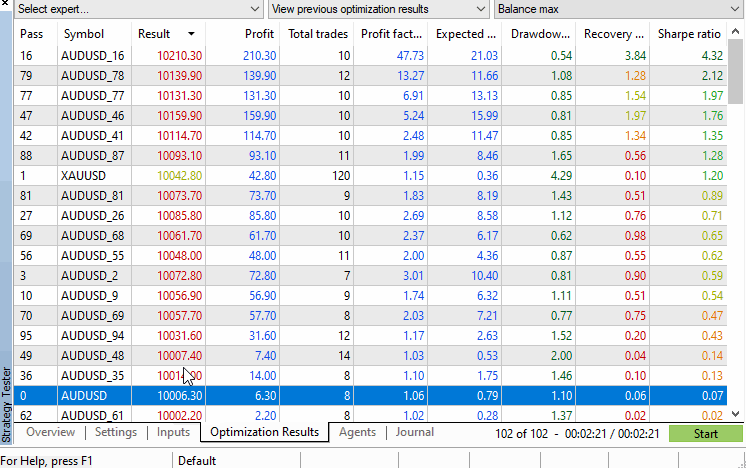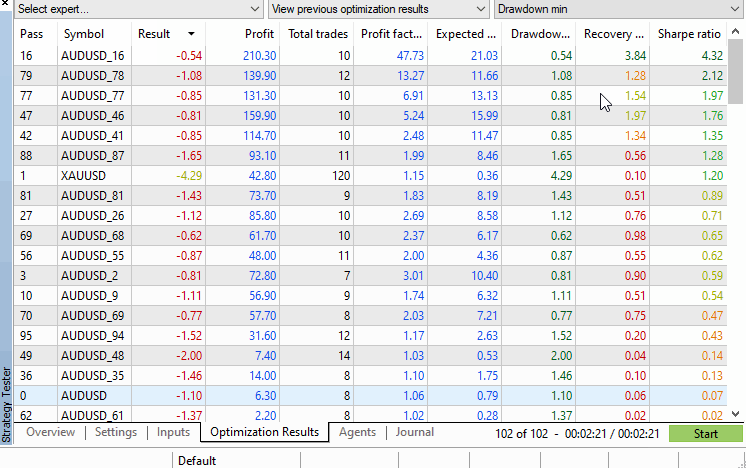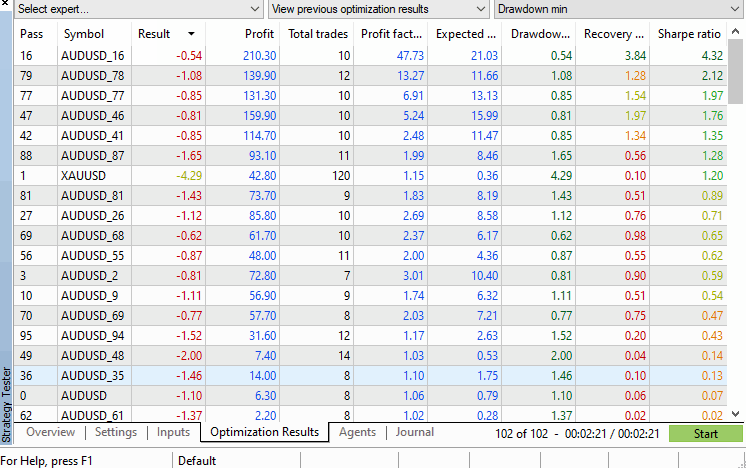
Auf der Registerkarte „Ergebnisse“ des Strategietesters werden alle Leistungsdaten angezeigt, die für uns von Interesse sein könnten, und die Symbole werden in absteigender Reihenfolge auf der Grundlage der ausgewählten Leistungskriterien angeordnet, die über das Dropdown-Menü in der oberen rechten Ecke des Testerfensters ausgewählt werden können. Von dieser Ansicht aus kann der p-Wert leicht manuell berechnet werden oder bei Bedarf automatisch durch Verarbeitung der .xml-Datei, die optional mit einem Rechtsklick aus dem Tester exportiert werden kann.

Anhand des Beispiels müssen wir nicht einmal Berechnungen anstellen, denn es ist zu erkennen, dass die Testwerte des Originalsymbols weit unten auf der Ergebnisliste stehen, während mehr als 10 permutierte Symbole eine bessere Leistung erzielen. Dies bedeutet, dass der p-Wert über 0,05 liegt.

Natürlich ist das Ergebnis dieses Tests mit Vorsicht zu genießen, da der gewählte Testzeitraum sehr kurz war. Die Nutzer sollten einen Testzeitraum wählen, der wesentlich länger ist und repräsentativ für die Bedingungen ist, die im realen Handel auftreten können.

Wie bereits erwähnt, gibt es viele Möglichkeiten, unsere Ergebnisse weiter zu verarbeiten, um die p-Werte zu berechnen. Alle weiteren Operationen konzentrieren sich auf das Parsen der Daten aus der vom Strategietester exportierten XML-Datei. Wir werden zeigen, wie man eine Tabellenkalkulationsanwendung verwenden kann, um die Datei mit ein paar Klicks und Tastendrücken zu bearbeiten.

Nachdem Sie die Datei exportiert haben, notieren Sie sich natürlich, wo sie gespeichert ist, und öffnen Sie sie mit einem beliebigen Tabellenkalkulationsprogramm. Die folgende Grafik zeigt die Verwendung des kostenlosen OpenOffice Calc, bei der eine neue Zeile am unteren Rand der Tabelle hinzugefügt wurde. Bevor Sie weitermachen, sollten Sie Zeilen mit Symbolen entfernen, die nicht in die Berechnungen einfließen sollen. Unter jeder entsprechenden Spalte wird der p-Wert mithilfe eines nutzerdefinierten Makros berechnet. Die Formel des Makros verweist auf die Leistungskennzahlen des permutierten Symbols (im gezeigten Dokument in Zeile 18) sowie auf die der permutierten Symbole für jede Spalte.  Die vollständige Formel für das Makro ist in der Grafik dargestellt.

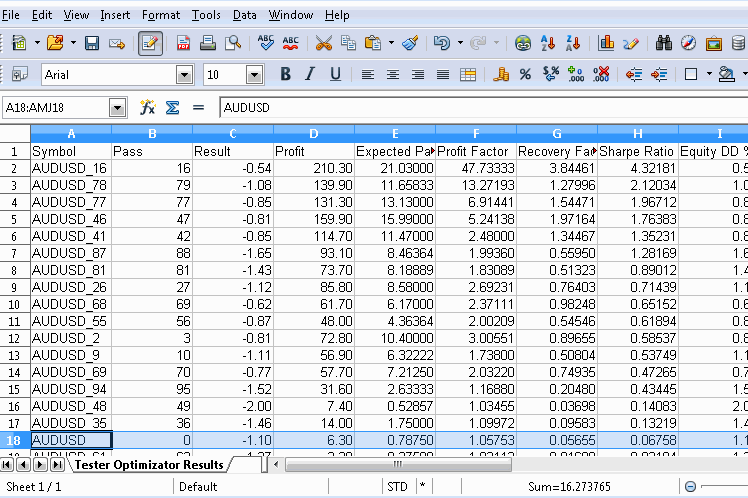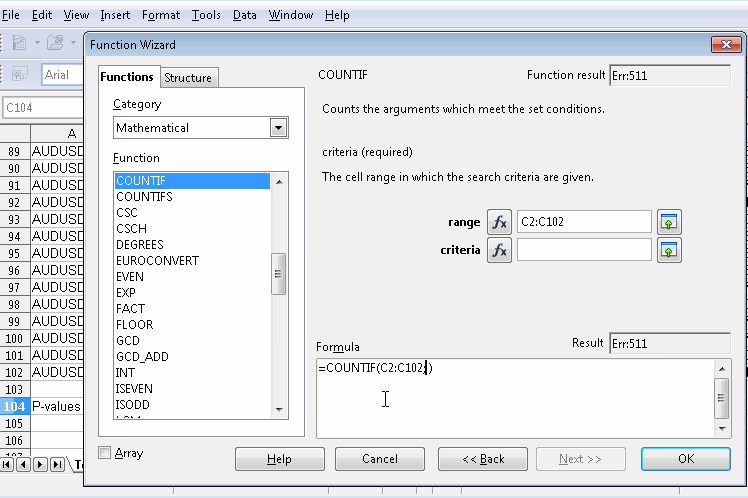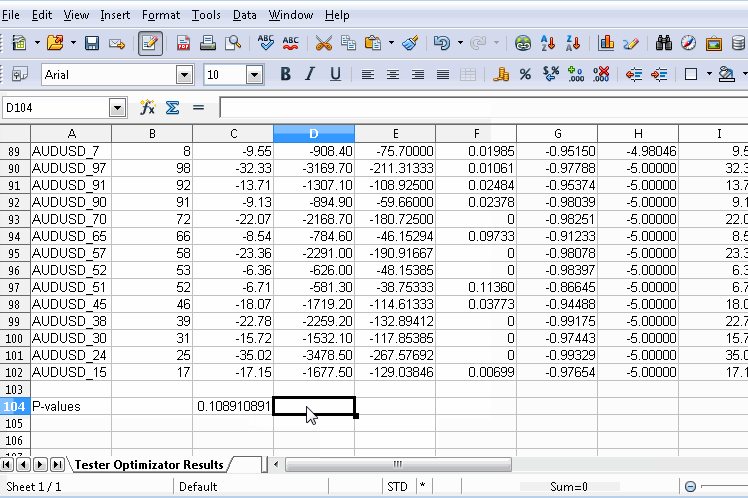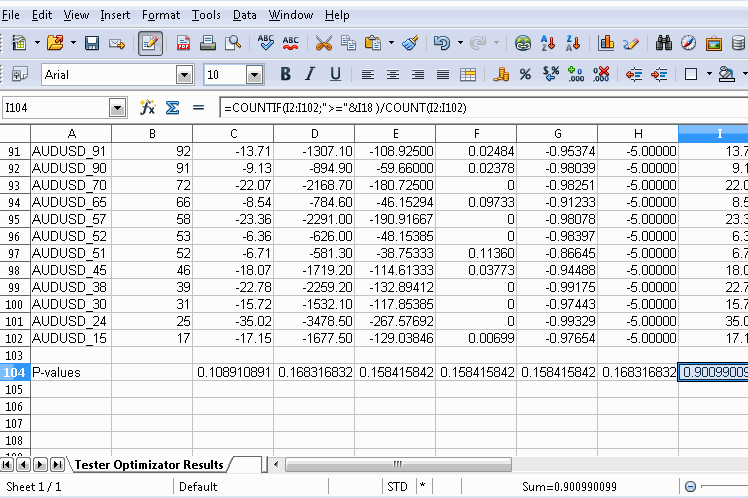
Neben einer Tabellenkalkulation könnten wir auch Python verwenden, das über eine Fülle von Modulen zum Parsen von XML-Dateien verfügt. Wenn ein Nutzer mql5 beherrscht, kann er die Dateien auch mit einem einfachen Skript parsen. Denken Sie nur daran, ein zugängliches Verzeichnis zu wählen, wenn Sie die Optimierungsergebnisse aus dem Testgerät exportieren.

Schlussfolgerung

Wir haben gezeigt, dass ein Permutationstest auf jeden EA angewendet werden kann, ohne Zugang zum Quellcode zu haben. Ein solcher Permutationstest ist von unschätzbarem Wert, da er ziemlich robuste Statistiken anwendet, die keine Annahmen über die Verteilung der beteiligten Daten erfordern. Im Gegensatz zu vielen anderen statistischen Tests, die bei der Strategieentwicklung eingesetzt werden.

Der größte Nachteil liegt im Zeitaufwand und in den Computerressourcen, die zur Durchführung des Tests benötigt werden. Dafür ist nicht nur ein leistungsfähiger Prozessor erforderlich, sondern auch eine beträchtliche Menge an Speicherplatz. Das Erzeugen neuer Ticks und Symbole verbraucht freien Speicherplatz auf Ihrer Festplatte. Meiner Meinung nach sollte jeder, der mit dem Kauf von EAs zu tun hat, diese Analysemethode zur Kenntnis nehmen. Sie kostet zwar Zeit, aber sie könnte Sie auch davor bewahren, schlechte Entscheidungen zu treffen, die Sie später teuer zu stehen kommen.

Analysen, die sich auf umgerechnete Preisdaten stützen, können auf verschiedene Weise durchgeführt werden.  Wir können die Methode verwenden, um das Verhalten von Indikatoren zu analysieren, sowie in verschiedenen Phasen der Strategieentwicklung. Die Möglichkeiten sind vielfältig. Bei der Entwicklung oder Erprobung von Strategien hat man manchmal den Eindruck, dass nicht genügend Daten vorhanden sind. Die Verwendung permutierter Preisreihen vervielfacht die Verfügbarkeit von Daten für Tests. Der Quellcode aller im Artikel beschriebenen mql5-Programme ist beigefügt, ich hoffe, die Leser werden sie nützlich finden.

Dateiname	Programmtyp	Beschreibung
GenerateSymbols.mqh	„#include“-Datei	Die Datei enthält die Definition der Klasse CGenerateSymbols zur Erzeugung von Symbolen mit aus einem ausgewählten Basissymbol permutierten Tickdaten.
NewSymbol.mqh	„#include“-Datei	enthält die Klassendefinition CNewSymbol zur Erstellung nutzerdefinierter Symbole.
PermuteTicks.mqh	„#include“-Datei	definiert die Klasse CPermuteTicks zur Erstellung von Permutationen eines Arrays von Tickdaten.
PrepareSymbolsForPermutationTests.mq5	Skript-Datei	Skript, das die Erstellung von nutzerdefinierten Symbolen mit permutiertem Tick zur Vorbereitung eines Permutationstests automatisiert.