[存档!]纯数学、物理学、化学等:与贸易没有任何关系的大脑训练问题 - 页 267 1...260261262263264265266267268269270271272273274...628 新评论 EvGen 2010.03.03 01:14 #2661 也就是说,你不能拿两个球出来,这是被禁止的。 Sceptic Philozoff 2010.03.03 01:14 #2662 马斯塔克,你现在是在蛊惑人心。你很清楚,问题是我们要把球拿出来多少次。 EvGen 2010.03.03 01:15 #2663 Mathemat >>: MaStak, ну ты ж ведь сейчас демагогией занимаешься. 我一直在寻找条件中的诀窍 - 我发现了它 ) Sceptic Philozoff 2010.03.03 01:18 #2664 好吧,明天给我看看你的解决方案。无论你拔出多少次,都是如此。而我们都会尝试一起优化它。我要去睡觉了,我必须早起。 EvGen 2010.03.03 01:28 #2665 是。 xx yy xy // 内容 xx yy xy // 铭文 成为了。 ** ** *y // 内容 xy xx yy // 铭文 一种是拉出来的,发现是 "y",问题是 "那又怎样?",现在我们对所有的人都知道了 ) 用经典的话说:"--这些信息对我来说是不够的。" vegetate 2010.03.03 03:57 #2666 MaStak >>: Было: xx yy xy // Содержимое xx yy xy // Надписи Стало: ** ** *y // Содержимое xy xx yy // Надписи Один как бы вытащили и узнали что это "y", и спрашивается "и чё ?", теперь известно всё о всех ) Говоря словами классика: "- Этой информации мне недостаточно." 够了,问题的陈述说明了一切:"每个盒子都 贴有与 内容不符 的铭文 "。 EvGen 2010.03.03 04:16 #2667 vegetate >>: Достаточно. в условии задачи все сказано "на каждой коробке стоит надпись, не соответствующая содержимому" xy xx yy // 铭文 --------- xx yy xy // 选项 yy xy xx --------- 是的,确实,1个球的xy ) 还有两个解决方案;D Sceptic Philozoff 2010.03.03 22:34 #2668 Vladimir Gomonov 2010.03.04 18:54 #2669 第一个和最后一个(a和c)是无法解决的。然而,第二个问题是可以解决的。 ! 点击。 在蓝色的那张纸上写了五次。 一次在红色的。 左边的绿色有一次。 中间的2次。 右边的3次。 Vladimir Gomonov 2010.03.04 19:24 #2670 对关于飞机和火箭的问题。 我不知道是谁提出的问题及其解决方案,但是......。 如果飞到一半后,火箭在小半圆的中间,而飞机在大四分之一圆的中间。那么小半圆的切线必须连接这两点(根据给定的解决方案)。 然而,情况并非如此,这立即证明了解决方案的不正确性。 我们被骗了,先生们!我们被骗了。 1...260261262263264265266267268269270271272273274...628 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
也就是说,你不能拿两个球出来,这是被禁止的。
马斯塔克,你现在是在蛊惑人心。你很清楚,问题是我们要把球拿出来多少次。
MaStak, ну ты ж ведь сейчас демагогией занимаешься.
我一直在寻找条件中的诀窍 - 我发现了它 )
好吧,明天给我看看你的解决方案。无论你拔出多少次,都是如此。而我们都会尝试一起优化它。我要去睡觉了,我必须早起。
是。
xx yy xy // 内容
xx yy xy // 铭文成为了。
** ** *y // 内容xy xx yy // 铭文
一种是拉出来的,发现是 "y",问题是 "那又怎样?",现在我们对所有的人都知道了 )
用经典的话说:"--这些信息对我来说是不够的。"
Было:
xx yy xy // Содержимое
xx yy xy // НадписиСтало:
** ** *y // Содержимоеxy xx yy // Надписи
Один как бы вытащили и узнали что это "y", и спрашивается "и чё ?", теперь известно всё о всех )
Говоря словами классика: "- Этой информации мне недостаточно."
够了,问题的陈述说明了一切:"每个盒子都 贴有与 内容不符 的铭文 "。
Достаточно. в условии задачи все сказано "на каждой коробке стоит надпись, не соответствующая содержимому"
xy xx yy // 铭文
---------
xx yy xy // 选项
yy xy xx
---------
是的,确实,1个球的xy )
还有两个解决方案;D
第一个和最后一个(a和c)是无法解决的。然而,第二个问题是可以解决的。
!
点击。
在蓝色的那张纸上写了五次。
一次在红色的。
左边的绿色有一次。
中间的2次。
右边的3次。
对关于飞机和火箭的问题。 我不知道是谁提出的问题及其解决方案,但是......。
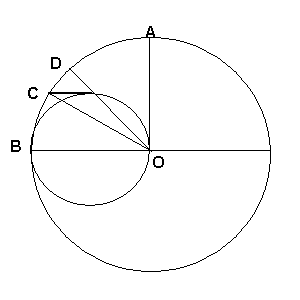
如果飞到一半后,火箭在小半圆的中间,而飞机在大四分之一圆的中间。那么小半圆的切线必须连接这两点(根据给定的解决方案)。
然而,情况并非如此,这立即证明了解决方案的不正确性。
我们被骗了,先生们!我们被骗了。