交易中的机器学习:理论、模型、实践和算法交易 - 页 3009 1...300230033004300530063007300830093010301130123013301430153016...3399 新评论 Forester 2023.04.09 14:39 #30081 СанСаныч Фоменко #: 但最重要的是,必须从理论上 证明现有特征的预测能力在未来不会发生变化,或者变化微弱。在整个蒸汽滚筒中,这是最重要的一点。 不幸的是,没有人发现这一点,否则他就不会在这里,而是在热带岛屿))))。 SanSanych Fomenko#: 在我看来,模型的作用极小,因为它与性状预测能力的稳定性无关:预测能力的稳定性是 "教师-性状 "对的属性。 是的,即使是一棵树或回归也能找到一种模式,只要它存在且不改变。 SanSanych Fomenko#: 1.还有人有分类误差小于 20% 的教师-特质对吗? 很简单。我可以取消生成几十个数据集。我现在正在研究 TP=50 和 SL=500。教师标注的平均误差为 10%。如果是 20%,那就是梅花模型了。 所以重点不在于分类误差,而在于所有盈亏相加的结果。 如您所见,顶级模型的误差为 9.1%,而您可以赚取误差为 8.3% 的东西。 图表只显示了 OOS,由 Walking Forward 获得,每周重训一次,5 年共重训 264 次。 有趣的是,模型在 0 时的分类误差为 9.1%,而 50/500 = 0.1,即应该为 10%。事实证明,1% 的误差(每条最小误差,实际误差会更大)。 Machine learning in trading: BolliToucher - Need EA Any rookie question, so mytarmailS 2023.04.09 15:10 #30082 首先,你必须意识到模型内部充满了垃圾...... 如果把训练有素的木质模型分解成内部规则和这些规则的统计数据。 比如 len freq err condition pred 315 3 0.002 0.417 X[,1]>7.49999999999362e-05 & X[,2]<=-0.00026499999999996 & X[,4]<=0.000495000000000023 1 483 3 0.000 0.000 X[,1]<=0.000329999999999941 & X[,8]>0.000724999999999976 & X[,9]>0.000685000000000047 1 484 3 0.002 0.273 X[,1]>0.000329999999999941 & X[,8]>0.000724999999999976 & X[,9]>0.000685000000000047 -1 555 3 0.001 0.333 X[,5]<=0.000329999999999941 & X[,7]>0.000309999999999921 & X[,8]<=-0.000144999999999951 -1 687 3 0.001 0.250 X[,2]<=-0.00348499999999996 & X[,7]<=-0.000854999999999939 & X[,9]<=-4.99999999999945e-05 1 734 3 0.003 0.000 X[,7]>-0.000854999999999939 & X[,8]>0.000724999999999865 & X[,9]<=0.000214999999999965 1 1045 3 0.003 0.231 X[,1]<=-0.000310000000000032 & X[,4]>0.000105000000000022 & X[,4]<=0.000164999999999971 -1 1708 3 0.000 0.000 X[,3]>0.00102499999999994 & X[,6]<=0.000105000000000022 & X[,7]<=-0.000650000000000039 1 1709 3 0.002 0.250 X[,3]>0.00102499999999994 & X[,6]<=0.000105000000000022 & X[,7]>-0.000650000000000039 -1 1984 3 0.001 0.000 X[,1]<=0.000329999999999941 & X[,8]>0.000724999999999976 & X[,9]>0.000674999999999981 1 2654 3 0.003 0.000 X[,4]<=0.00205000000000011 & X[,5]>0.0014550000000001 & X[,9]<=0.00132999999999994 1 2655 3 0.000 0.000 X[,4]<=0.00205000000000011 & X[,5]>0.0014550000000001 & X[,9]>0.00132999999999994 -1 2656 3 0.001 0.200 X[,3]<=0.00245499999999998 & X[,4]>0.00205000000000011 & X[,5]>0.0014550000000001 -1 2657 3 0.000 0.000 X[,3]>0.00245499999999998 & X[,4]>0.00205000000000011 & X[,5]>0.0014550000000001 1 2852 3 0.000 0.000 X[,2]<=-0.001135 & X[,8]>-0.000130000000000075 & X[,8]>0.00128499999999998 -1 2979 3 0.001 0.200 X[,1]>0.000930000000000097 & X[,1]>0.00129000000000012 & X[,8]<=-0.000275000000000025 -1 并分析规则 错误 的误差与它在样本中出现的频率的关系。 我们得到 那么我们对这一区域感兴趣 规则非常有效,但却非常罕见,以至于我们有理由怀疑其统计数据的真实性,因为 10-30 个观测值并不是统计数据 Maxim Dmitrievsky 2023.04.09 15:14 #30083 mytarmailS #:首先,你必须意识到模型内部充满了垃圾...如果把一个训练有素的木质模型分解成内部规则和这些规则的统计数据,就会发现:就像分析规则 误差 与规则在样本中出现频率 的关系我们得到 这只是近期文章黑暗中的一缕阳光如果能正确分析模型的误差,就能发现一些有趣的东西。我们将非常迅速地接受您的请求,且无需任何 Gpu、短信和注册。 mytarmailS 2023.04.09 15:22 #30084 Maxim Dmitrievsky #: 近期文章中的一缕阳光 如果您能正确分析模型错误,就能发现一些有趣的东西。我们会很快接受,不需要任何 gpu、短信和注册。 如果有的话,会有一篇相关文章。 Maxim Dmitrievsky 2023.04.09 15:33 #30085 mytarmailS #:如果有的话,会有相关文章的。 诺姆,我的上一篇文章也是关于同样的事情。但如果你的方法更快,那就更好了。 mytarmailS 2023.04.09 16:02 #30086 Maxim Dmitrievsky #: 诺姆,我的上一篇文章讲的也是这个问题。但如果你的方法更快,那就更好了。 什么叫更快? Maxim Dmitrievsky 2023.04.09 16:28 #30087 mytarmailS #:什么叫 "更快"? 就速度而言。 mytarmailS 2023.04.09 16:41 #30088 Maxim Dmitrievsky #: 就速度而言 5 千米取样约需 5-15 秒 Maxim Dmitrievsky 2023.04.09 16:44 #30089 mytarmailS #:在 5 千米样本上大约需要 5-15 秒。 我指的是从开始到获得 TC 的整个过程。 我有两个模型被重新训练了好几次,所以速度不是很快,但还可以接受。 最后我也不知道他们到底筛选出了什么。 mytarmailS 2023.04.09 16:51 #30090 Maxim Dmitrievsky #:我是说,从一开始到获得 TC 的整个过程。我有 2 个模型被重新训练了好几次,所以速度不是很快,但还可以接受。最后,我不知道他们到底筛选出了什么。 训练 5k。 有效 60k。 模型训练 - 1-3 秒 规则提取 - 5-10 秒 检查每条规则(20-30k 条)的有效性 60k 1-2 分钟 当然,一切都是近似值,取决于特征和数据的数量 1...300230033004300530063007300830093010301130123013301430153016...3399 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
但最重要的是,必须从理论上 证明现有特征的预测能力在未来不会发生变化,或者变化微弱。在整个蒸汽滚筒中,这是最重要的一点。
不幸的是,没有人发现这一点,否则他就不会在这里,而是在热带岛屿))))。
是的,即使是一棵树或回归也能找到一种模式,只要它存在且不改变。
1.还有人有分类误差小于 20% 的教师-特质对吗?
很简单。我可以取消生成几十个数据集。我现在正在研究 TP=50 和 SL=500。教师标注的平均误差为 10%。如果是 20%,那就是梅花模型了。
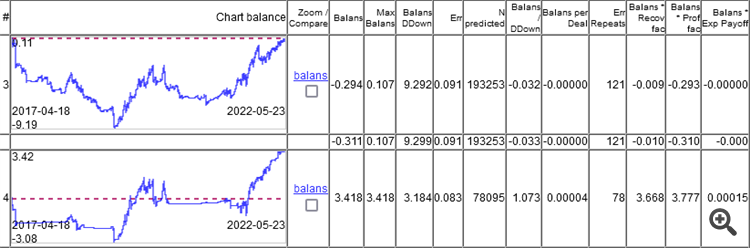
所以重点不在于分类误差,而在于所有盈亏相加的结果。
如您所见,顶级模型的误差为 9.1%,而您可以赚取误差为 8.3% 的东西。
图表只显示了 OOS,由 Walking Forward 获得,每周重训一次,5 年共重训 264 次。
有趣的是,模型在 0 时的分类误差为 9.1%,而 50/500 = 0.1,即应该为 10%。事实证明,1% 的误差(每条最小误差,实际误差会更大)。
首先,你必须意识到模型内部充满了垃圾......
如果把训练有素的木质模型分解成内部规则和这些规则的统计数据。
比如
并分析规则 错误 的误差与它在样本中出现的频率的关系。
我们得到
那么我们对这一区域感兴趣
规则非常有效,但却非常罕见,以至于我们有理由怀疑其统计数据的真实性,因为 10-30 个观测值并不是统计数据
首先,你必须意识到模型内部充满了垃圾...
如果把一个训练有素的木质模型分解成内部规则和这些规则的统计数据,就会发现:
就像
分析规则 误差 与规则在样本中出现频率 的关系
我们得到
近期文章中的一缕阳光
如果有的话,会有一篇相关文章。
如果有的话,会有相关文章的。
诺姆,我的上一篇文章讲的也是这个问题。但如果你的方法更快,那就更好了。
什么叫更快?
什么叫 "更快"?
就速度而言
5 千米取样约需 5-15 秒
在 5 千米样本上大约需要 5-15 秒。
我指的是从开始到获得 TC 的整个过程。
我有两个模型被重新训练了好几次,所以速度不是很快,但还可以接受。
最后我也不知道他们到底筛选出了什么。
我是说,从一开始到获得 TC 的整个过程。
我有 2 个模型被重新训练了好几次,所以速度不是很快,但还可以接受。
最后,我不知道他们到底筛选出了什么。
训练 5k。
有效 60k。
模型训练 - 1-3 秒
规则提取 - 5-10 秒
检查每条规则(20-30k 条)的有效性 60k 1-2 分钟
当然,一切都是近似值,取决于特征和数据的数量