您应当知道的 MQL5 向导技术（第 09 部分）：K-Means 聚类与分形波配对
667
0
概述
本文继续深入研究 “k-均值” 聚类，探讨借助 MQL5 向导实现和测试简单思路的可能性。这与我们在上一篇文章中讲述的 AHC 一样，是一种对数据进行分类的无监督方式。
故此，在我们跃入之前，回顾一下我们在 AHC 下涵盖的内容，并看看它与 “k-均值”聚类的对比，也许会有所帮助。聚集层次化聚类算法，通过把数据集中的每个数据点分类，当作聚类来初始化。 然后，该算法会根据接近程度，将它们迭代合并到聚集之中。典型情况下，聚类的数量不能预判，但分析人员可以通过查看构造的树状图来判定，树状图是所有数据点合并到单个聚类后的最终输出。不然的话，会如我们在之前文章中看到的那样，如果分析人员脑海里有一定数量的聚类集，那么输出树状图将在聚类数量与分析人员的初始数字相匹配的水平/高度处终止。事实上，根据树状图的切断之处，可以获得不同的聚类。
另一方面，“K-均值” 聚类首先基于分析师的预设数字随机选择聚类中心（质心）。 然后判定每个数据点与其最近中心的 方差，并迭代调整中心/质心值，直到每个聚类的方差最小。
默认情况下，“k-均值” 实际上非常缓慢且效率低下，这就是为什么它通常被称为朴素 “k-均值”，“朴素”意味着有更快的实现。这种苦差事的一部分源于在优化开始时，数据集是随机分配初始质心。此外，在随机选择质心之后，通常运用 劳埃德（Lloyd）算法 来求出到达的正确质心，从而得出类别值。劳埃德算法有一些补充和替代方案，其中包括：Jenks 的自然断层，它侧重于聚类均值，而不是到所选质心的距离；顾名思义，“K-中位数”取聚类中位数而非质心、或均值，作为指导朝向理想分类的代理；根据维基百科，使用每个集群内的实际数据点作为潜在质心的 “k-中位数”，从而针对噪声和异常值更具健壮性；最后是模糊式聚类，其中聚类边界未明确切割，其中数据点能够、且倾向于属于多个聚类。最后一种格式很有趣，因为并非对每个数据点进行“分类”，而是分配一个回归权重，则给定数据点属于每个适用集群的程度得以量化。
本文的意图是展示另一种被标榜为更有效的 “k-均值”实现，即 “k-均值++”。该算法依赖于劳埃德方法，像是默认的朴素 “k-均值”，但它在选择随机质心朝向的初始方式有所不同。这种方式不像朴素的 “k-均值”那样“随机”，因此，它往往比后者更快、更有效地收敛。
算法比较
“K-均值” 与 “K-中位数”
“K-均值” 最小化聚类点与其质心之间的欧几里得距离平方，而 “k-中位数” 最小化给定聚类（L1-Norm）质心与其中位数的绝对距离之和。这种区别颇有争议，令 “k-中位数”不易受到异常值的影响，并且令聚类更好地代表所有数据点，因为聚类中心是所有点的中位数，而非它们的均值。计算方式也不同，因为 “k-中位数” 依赖于基于 “L1-Norm” 算法，而 “k-均值” 则用 “k-均值++” 和劳埃德算法。因此，在用例中，“k-均值” 更有能力处理球形或均匀扩散的数据集，而 “k-中位数” 可能更擅长处理不规则和形状奇特的数据集。最后，在解释方面，“k-中位数” 也往往是首选，因为中位数往往比它们的均值更能代表一个集群。
“K-均值” 对比 “Jenks 自然断层”
与 “k-均值” 一样，“Jenks 自然断层” 算法旨在尽可能减少数据点到质心的距离，其中细微的区别在于该算法还尝试将这些类抛得尽可能远，如此它们就可以被区分。这是通过识别数据的“自然分组”来达成的。在聚类内部，方差明显增加的数据点处，这些“自然分组”很容易被识别出，故这些点被谓之断层，这就是算法得名的地方。通过把每个聚类内的方差最小化来强调断层。它更适合样式数据集的分类，而不是回归或连续类型。凭所有这些，像 “k-中位数” 算法，与典型的 “k-均值” 相比，它对于异常值的敏感度，以及整体解释方面具有优势。
“K-均值” 对比 “K-中位数”
如前所述，“K-中位数” 最初依赖于实际数据，而不是名义上的质心点。在这一层面，它很像集聚层次化分类，但此处没有树状图可绘制。选定数据点当作质心，其与聚类中所有其它数据点距离最小。这种选择还可以采用各种距离测量技术，包括曼哈顿（Manhattan）距离、或余弦相似度。由于质心是实际的数据点，因此可以说，与 Junks 和 ”K-中位数“ 一样，它们比 ”k-均值“ 更能代表其基础数据，但是它们的计算效率更低，尤其是在处理大型数据集之时。
”K-均值“ 对比 模糊聚类
如前所述，模糊聚类为每个数据点提供回归权重，该权重将采用矢量格式，具体取决于正在发挥作用的聚类数量。通过使用模糊原型（隶属函数），每个聚类的权重将在 0.0 – 1.0 范围内，这与判定质心的 ”k-均值“ 不同。这倾向于提供更多信息，故可更好地代表数据。在上述所有点上，它的得分都超过了典型的 ”k-均值“，而主要缺点是计算势必会像人们预期的那样剧烈。
K-均值++
为了令朴素 “k-均值” 聚类更有效，典型情况下，在本文中，使用 “k-均值++” 初始化，其中初始质心的随机性较低，但在数据中的扩散更遵循比例。从测试中可以看出，求解速度要快得多，并且会收敛到目标质心。达成了更好的整体聚类品质，并且不仅对异常数据点、亦对质心点的初始选择敏感性降低。
数据
正如我们在关于聚集层次化聚类的文章中实现的那样，我们将使用 AlgLib 的现成 “K-均值” 类来开发一种简单、且与我们在该文章中类似的算法，看看我们是否可以获得交叉验证的结果。要测试的证券是 GBPUSD，我们在 2022.01.01 到 2023.02.01 区间运行测试，然后从该日期到 2023.10.01 执行前瞻测试。我们将采用日线时间帧，并在测试期间基于真实即刻报价执行最终运行。
结构
组织聚类的数据结构，与我们在 AHC 文章中的内容雷同，实际上使用的过程和信号的思路大多相同。主要区别在于，当我们运用集聚聚类时，我们必须运行一个函数来提取与目标聚类编号匹配的同级别聚类，故此我们调用函数 “ClusterizerGetKClusters”，我们在此不这样做。此外，我们还必须格外小心，确保结构真的收到价格信息，为此，我们检查了很多无效数字，如以下摘要片段所示：
double _dbl_min=-1000.0,_dbl_max=1000.0; for(int i=0;i<m_training_points;i++) { for(int ii=0;ii<m_point_features;ii++) { double _value=m_close.GetData(StartIndex()+i)-m_close.GetData(StartIndex()+ii+i+1); if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; } m_data.x.Set(i,ii,_value); matrix _m=m_data.x.ToMatrix();if(_m.HasNan()){ _m.ReplaceNan(0.0); }m_data.x=CMatrixDouble(_m); } if(i>0)//assign classifier only for data points for which eventual bar range is known { double _value=m_close.GetData(StartIndex()+i-1)-m_close.GetData(StartIndex()+i); if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; } m_data.y.Set(i-1,_value); vector _v=m_data.y.ToVector();if(_v.HasNan()){ _v.ReplaceNan(0.0); }m_data.y=CRowDouble(_v); } }
ALGLIB
AlgLib 库在本系列文章中已被大量引用，故我们将直接跳到形成聚类的代码。库中的两个函数是我们的重点，“SelectInitialCenters” 对于加快整个过程至关重要，因为如前所述，过于随机的初始聚类选择，往往会拖延收敛到正确聚类的时间。一旦运行该函数，我们将使用劳埃德算法来优调初始聚类选择，为此我们转向 “KMeansGenerateInternal” 函数。
选择初始聚类的可用函数能通过以下 3 种方式之一完成，要么随机完成，要么使用 “k-均值++”，要么使用快速贪婪初始化。我们来每样简要回顾一下。与其它 2 种情况一样，通过随机聚类选择，输出的聚类被存储在名为 “ct” 的输出矩阵之中，其中每行表示一个聚类，令 “ct” 的行数与预期的聚类数量匹配，而列数将等于数据集中每个数据点的特征或向量基数。故此，随机选项只是为每行 “ct” 分配一次从输入数据集中随机选择的数据点。如下所示：
//--- Random initialization if(initalgo==1) { for(i=0; i<k; i++) { j=CHighQualityRand::HQRndUniformI(rs,npoints); ct.Row(i,xy[j]+0); } return; }
依据 “K-均值++”，我们也从选择一个随机中心开始，但仅限于第一个聚类，不同于之前我们真对所有聚类都这样做。然后，我们测量每个数据集点与随机选择的聚类中心之间的距离，记录每行（或潜在聚类）的这些距离的平方和，如果该总和为零，我们只需为该聚类选择一个随机质心。对于存储在变量 's' 中的所有非零和，我们选择的点离随机选择的初始聚类最远。代码相当复杂，但摘要片段都带有注释，可以提供更多启示：
//--- k-means++ initialization if(initalgo==2) { //--- Prepare distances array. //--- Select initial center at random. initbuf.m_ra0=vector<double>::Full(npoints,CMath::m_maxrealnumber); ptidx=CHighQualityRand::HQRndUniformI(rs,npoints); ct.Row(0,xy[ptidx]+0); //--- For each newly added center repeat: //--- * reevaluate distances from points to best centers //--- * sample points with probability dependent on distance //--- * add new center for(cidx=0; cidx<k-1; cidx++) { //--- Reevaluate distances s=0.0; for(i=0; i<npoints; i++) { v=0.0; for(j=0; j<=nvars-1; j++) { vv=xy.Get(i,j)-ct.Get(cidx,j); v+=vv*vv; } if(v<initbuf.m_ra0[i]) initbuf.m_ra0.Set(i,v); s+=initbuf.m_ra0[i]; } // //--- If all distances are zero, it means that we can not find enough //--- distinct points. In this case we just select non-distinct center //--- at random and continue iterations. This issue will be handled //--- later in the FixCenters() function. // if(s==0.0) { ptidx=CHighQualityRand::HQRndUniformI(rs,npoints); ct.Row(cidx+1,xy[ptidx]+0); continue; } //--- Select point as center using its distance. //--- We also handle situation when because of rounding errors //--- no point was selected - in this case, last non-zero one //--- will be used. v=CHighQualityRand::HQRndUniformR(rs); vv=0.0; lastnz=-1; ptidx=-1; for(i=0; i<npoints; i++) { if(initbuf.m_ra0[i]==0.0) continue; lastnz=i; vv+=initbuf.m_ra0[i]; if(v<=vv/s) { ptidx=i; break; } } if(!CAp::Assert(lastnz>=0,__FUNCTION__": integrity error")) return; if(ptidx<0) ptidx=lastnz; ct.Row(cidx+1,xy[ptidx]+0); } return; }
如常，AlgLib 确实共享了一些公开文档，故这可作为任何深入澄清的参考。
最后，快速贪婪初始化算法，其灵感来自一种称为 “k-均值++” 的 “k-均值” 变体，执行多轮，在每轮中：计算最接近当前选定质心的距离；然后按预期聚类大小的大约一半进行独立采样，其中选择某个点的概率，与其距当前质心的距离成正比，重复此操作，直到采样点数量是填满聚类的两倍；然后，依据选定的超大样本执行“贪婪选择”，直到获得较小的样本大小，优先级给予离质心最远的点。一个计算非常密集和复杂的过程，其代码带有注释如下：
//--- "Fast-greedy" algorithm based on "Scalable k-means++". //--- We perform several rounds, within each round we sample about 0.5*K points //--- (not exactly 0.5*K) until we have 2*K points sampled. Before each round //--- we calculate distances from dataset points to closest points sampled so far. //--- We sample dataset points independently using distance xtimes 0.5*K divided by total //--- as probability (similar to k-means++, but each point is sampled independently; //--- after each round we have roughtly 0.5*K points added to sample). //--- After sampling is done, we run "greedy" version of k-means++ on this subsample //--- which selects most distant point on every round. if(initalgo==3) { //--- Prepare arrays. //--- Select initial center at random, add it to "new" part of sample, //--- which is stored at the beginning of the array samplesize=2*k; samplescale=0.5*k; CApServ::RMatrixSetLengthAtLeast(initbuf.m_rm0,samplesize,nvars); ptidx=CHighQualityRand::HQRndUniformI(rs,npoints); initbuf.m_rm0.Row(0,xy[ptidx]+0); samplescntnew=1; samplescntall=1; initbuf.m_ra1=vector<double>::Zeros(npoints); CApServ::IVectorSetLengthAtLeast(initbuf.m_ia1,npoints); initbuf.m_ra0=vector<double>::Full(npoints,CMath::m_maxrealnumber); //--- Repeat until samples count is 2*K while(samplescntall<samplesize) { //--- Evaluate distances from points to NEW centers, store to RA1. //--- Reset counter of "new" centers. KMeansUpdateDistances(xy,0,npoints,nvars,initbuf.m_rm0,samplescntall-samplescntnew,samplescntall,initbuf.m_ia1,initbuf.m_ra1); samplescntnew=0; //--- Merge new distances with old ones. //--- Calculate sum of distances, if sum is exactly zero - fill sample //--- by randomly selected points and terminate. s=0.0; for(i=0; i<npoints; i++) { initbuf.m_ra0.Set(i,MathMin(initbuf.m_ra0[i],initbuf.m_ra1[i])); s+=initbuf.m_ra0[i]; } if(s==0.0) { while(samplescntall<samplesize) { ptidx=CHighQualityRand::HQRndUniformI(rs,npoints); initbuf.m_rm0.Row(samplescntall,xy[ptidx]+0); samplescntall++; samplescntnew++; } break; } //--- Sample points independently. for(i=0; i<npoints; i++) { if(samplescntall==samplesize) break; if(initbuf.m_ra0[i]==0.0) continue; if(CHighQualityRand::HQRndUniformR(rs)<=(samplescale*initbuf.m_ra0[i]/s)) { initbuf.m_rm0.Row(samplescntall,xy[i]+0); samplescntall++; samplescntnew++; } } } //--- Run greedy version of k-means on sampled points initbuf.m_ra0=vector<double>::Full(samplescntall,CMath::m_maxrealnumber); ptidx=CHighQualityRand::HQRndUniformI(rs,samplescntall); ct.Row(0,initbuf.m_rm0[ptidx]+0); for(cidx=0; cidx<k-1; cidx++) { //--- Reevaluate distances for(i=0; i<samplescntall; i++) { v=0.0; for(j=0; j<nvars; j++) { vv=initbuf.m_rm0.Get(i,j)-ct.Get(cidx,j); v+=vv*vv; } if(v<initbuf.m_ra0[i]) initbuf.m_ra0.Set(i,v); } //--- Select point as center in greedy manner - most distant //--- point is selected. ptidx=0; for(i=0; i<samplescntall; i++) { if(initbuf.m_ra0[i]>initbuf.m_ra0[ptidx]) ptidx=i; } ct.Row(cidx+1,initbuf.m_rm0[ptidx]+0); } return; }
该过程为下一阶段确保代表质心和效率。
选择初始质心后，它进入劳埃德算法，这是 “KMeansGenerateInternal” 中的核心功能。AlgLib 的实现看似很复杂，但劳埃德算法的基本原理是迭代搜索每个聚类的质心，然后通过将数据点从一个聚类移动到另一个聚类来重新定义每个聚类，如此聚类内部每个组成点至其质心的距离最小化。
至于本文，就像我们讲述树状图的片段一样，数据集点只是证券收盘价的变化，在我们的测试中是 GBPUSD。
预测
像 AHC 这样的 “K-均值” 本质上是一种无监督分类，故如前，如果我们想做任何回归或预测，我们需要附加 “y” 列数据，其滞后于我们的聚类数据集。由此，这个 “y” 数据也是收盘价的变化，但比聚类数据早 1 根柱线，以便有效地标记聚类，且为了提高效率，“y” 数据集和聚类的 x 矩阵数据集在同一 for 循环里填充。这在下面的摘要清单中有所说明：
if(i>0)//assign classifier only for data points for which eventual bar range is known { double _value=m_close.GetData(StartIndex()+i-1)-m_close.GetData(StartIndex()+i); if(_dbl_min>=_value||!MathIsValidNumber(_value)||_value>=_dbl_max){ _value=0.0; } m_data.y.Set(i-1,_value); vector _v=m_data.y.ToVector();if(_v.HasNan()){ _v.ReplaceNan(0.0); }m_data.y=CRowDouble(_v); }
一旦 “x” 矩阵和 “y” 数组填充了数据，聚类定义就会按照上面提到的步骤进行，然后识别当前收盘价变化的聚类，或 “x” 矩阵的顶行。由于它与其它数据点一起被处理为聚类，因此它将具有聚类索引。通过这个聚类索引，我们将其与已经“标记”的数据点进行比较，这些数据点的最终收盘价变化是已知的，从而获得这些最终变化的总和。依据该总和，我们可以很容易地得到平均变化，当我们用当前范围（或波动率）进行常规化时，它为我们提供了 0–1 范围内的权重。
//+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalKMEANS::ShortCondition(void) { ... double _output=GetOutput(); int _range_size=1; double _range=m_high.GetData(m_high.MaxIndex(StartIndex(),StartIndex()+_range_size))-m_low.GetData(m_low.MinIndex(StartIndex(),StartIndex()+_range_size)); _output/=fmax(_range,m_symbol.Point()); _output*=100.0; if(_output<0.0){ result=int(fmax(-100.0,round(_output)))*-1; } ... }
“LongCondition” 和 “ShortCondition” 函数返回 0 - 100 范围内的数值，因此我们的常规化数值必须乘以 100。
评估和结果
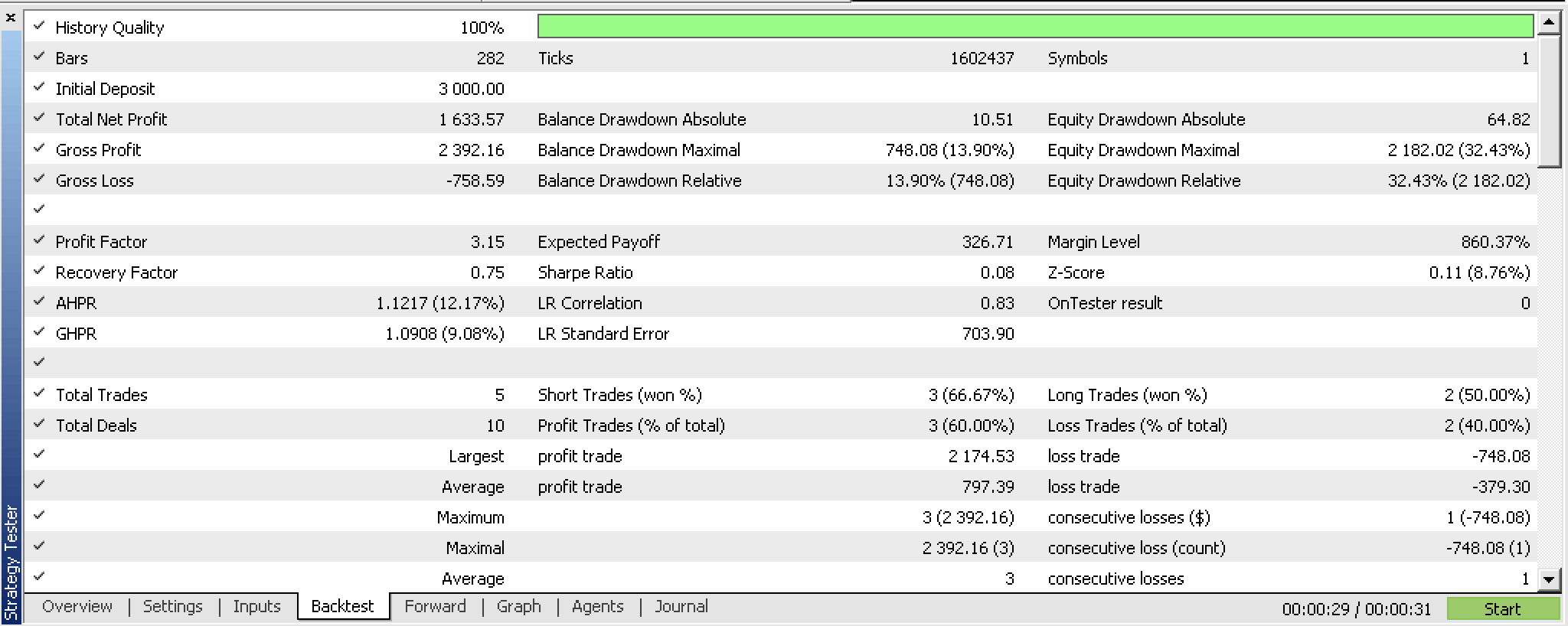
在 2022.01.01 到 2023.02.01 期间的回测中，我们得到了以下报告：
该报告依赖于来自优化运行中获得的以下输入：
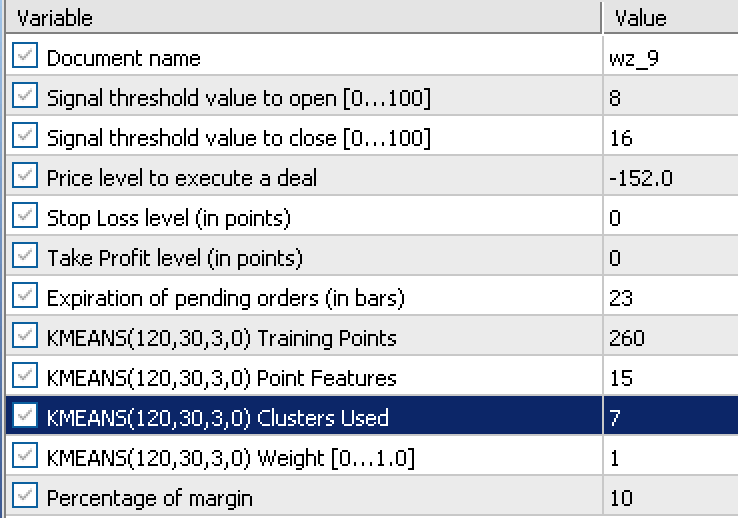
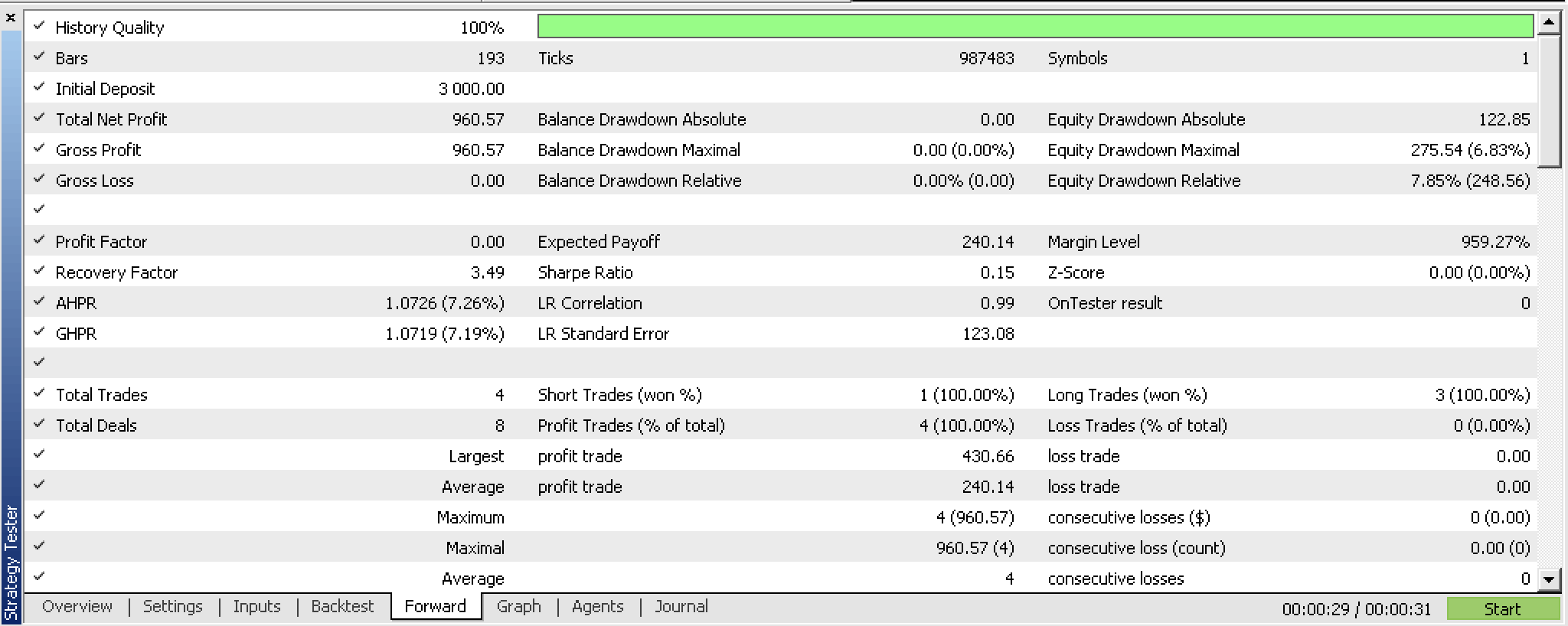
按该设置从 2023.02.02 到 2023.10.01 进行前瞻测试，我们获得以下报告：
在这个短暂的测试窗口内，它有点前景，但应如常一样，建议在覆盖更长时间段内进行更多的测试。
配合分形波浪实现
现在我们来研究一个选项，它采用来自分形指标的数据，而非收盘价的变化。分形指标开箱即用有点挑战性，尤其当尝试在智能系统里实现它时，因为缓冲区刷新后，在每个索引处并不包含指标值或价格。您需要检查缓冲区的每个索引，看看是否确实存在“分形”（即价格），如果它没有“分形”，则默认占位符是最大双精度值。这就是我们在修订后的 “GetOutput” 函数中如何准备分形数据的：
//+------------------------------------------------------------------+ //| Get k-means cluster output from identified cluster. | //+------------------------------------------------------------------+ double CSignalKMEANS::GetOutput() { ... int _size=m_training_points+m_point_features+1,_index=0; for(int i=0;i<m_fractals.Available();i++) { double _0=m_fractals.GetData(0,i); double _1=m_fractals.GetData(1,i); if(_0!=DBL_MAX||_1!=DBL_MAX) { double _v=0.0; if(_0!=DBL_MAX){_v=_0;} if(_1!=DBL_MAX){_v=_1;} if(!m_loaded){ m_wave[_index]=_v; _index++; } else { for(int i=_size-1;i>0;i--){ m_wave[i]=m_wave[i-1]; } m_wave[0]=_v; break; } } if(_index>=int(m_wave.Size())){ break; } } if(!m_loaded){ m_loaded=true; } if(m_wave[_size-1]==0.0){ return(0.0); } ... ... }
为了获得实际的价格分形，我们首先需要正确刷新分形指标对象。一旦完成，我们需要获取缓冲区可用索引的总数，该值表示在寻找分形价格点时，我们的 for 循环需要遍历多少个索引。进行时，我们需要注意分形指标有 2 个缓冲区，索引为 0 和 1。0-缓冲区索引是分形高点，而 1-索引缓冲区则是分形低点。这意味着在我们的 for 循环中，我们将按索引同时检查 2 个缓冲区的分形价格点，当其中任何一个记录了价格时（同一时间只能有其中一个缓冲区记录了价格 — 译者按：巨幅振荡有可能造成同一根柱线既是高点亦是低点），我们将该处数值添加到我们的向量 “m_wave” 之中。
现在，典型情况下可用的分形指数的数量有限，它可以作为我们对分形价格点的搜索限制。这意味着，即使我们想说有 12 个指数的波浪缓冲区，我们最终也可能在第一次运行、或最先的价格柱上只检索到 3 个。这意味着我们的波浪缓冲区需要像一个正常缓冲区一样的作用，保存它能够检索到的任何价格指数，并等待新的分形价格何时可用，如此就可将其添加到缓冲区之中。该过程会继续，直到缓冲区被填满。同时，由于缓冲区尚未填满或初始化，智能系统将无法处理任何信号，实质上依然处于初始化阶段。
因此，这就需要重视用于获取分形的缓冲区的大小。由于这些分形是 “k-均值” 聚类算法的输入，因此使用分形价格变化的系统，意味着该缓冲区的大小是训练点数量、特征数量和 1 的总和。我们在最后加上 1，因为即使我们的输入数据矩阵只需要训练点加上特征，额外的行是当前尚未回归点所在的行，即我们还没有 “y” 值。
如此，这种不幸的勤勉是必要的，但是一旦我们经历了这一点，我们就会获得以波浪形态整理过的价格信息。此处的论点是每个波浪顶点之间的变化，即分形价格点，可以替代我们在首次实现中所用的收盘价变化。
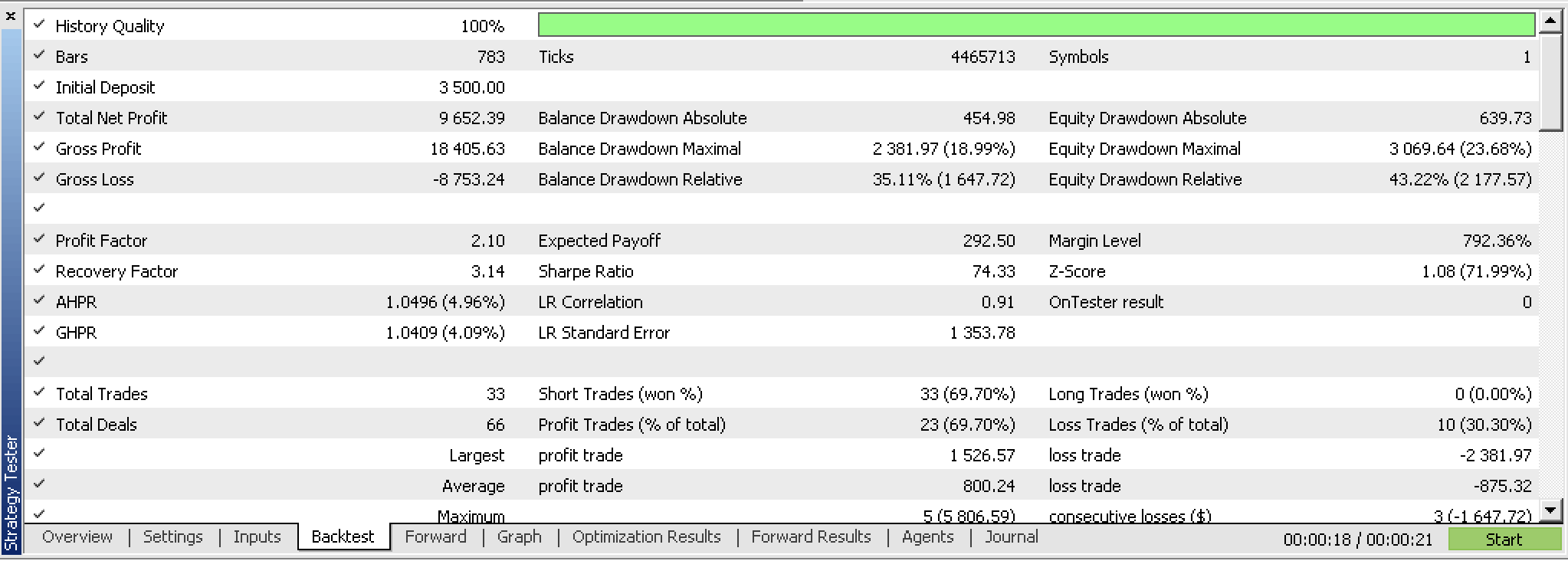
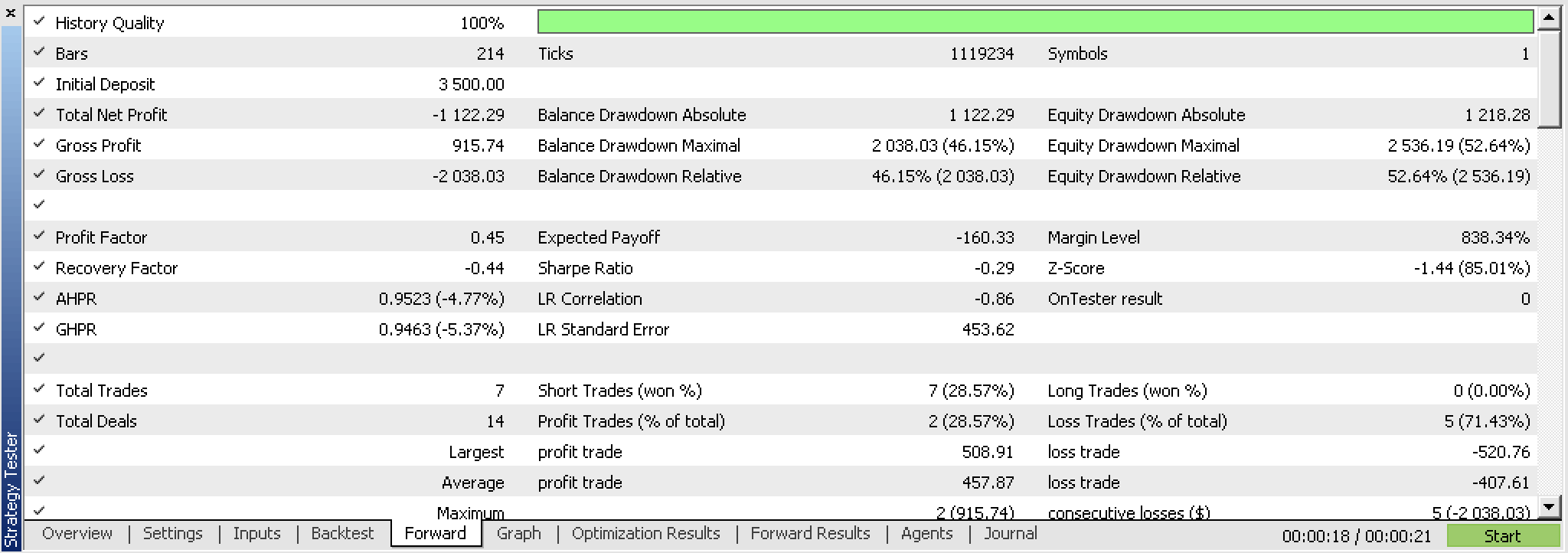
具有讽刺意味的是，在测试这个新的智能交易系统时，我们不能随意像以前那样按收盘价变化离场（TP 和 SL），而是只得用 TP 替代进行测试。在测试之后，即使回测很有前景，我们也无法像按收盘价格变化时那样依据最优结果，得到可盈利的前瞻测试。以下是报告。
如果我们看一下这些交易的连续、不间断的净值图形，我们可以清楚地看到，尽管先期运行的回测很有前景，但前瞻测试并不乐观。
这从根本上意味着该思路需要复审，其中一个起点可能是重新审视分形指标，也许有一个自定义版本，这对于初学者来说更有效，因为它只有分形价格点，其次可以利用一些输入进行定制，或可指导或量化每个分形点之间的最小价格移动量。
结束语
总而言之，我们已经研究了 “k-均值” 聚类，以及如何借助 AlgLib 实现在两种不同的设置中开箱即用，即原始收盘价和分形价格数据。
在初步阶段，对这两种设置的交叉验证测试产生了不同的结果，原始收盘价系统似乎比分形价格方式更有前景。我们已经分享了一些为何如此的原因，以及分享中所用的源代码，如下。
参考
附录
为了使用附带源代码，参考有关 MQL5 向导的 这篇文章 更能有所帮助。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/13915
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
软件开发和 MQL5 中的设计模式（第 2 部分）：结构模式
如何利用 MQL5 创建简单的多币种智能交易系统（第 5 部分）：凯尔特纳（Keltner）通道上的布林带 — 指标信号
