您应当知道的 MQL5 向导技术（第 08 部分）：感知器

概述

MQL5 向导 Expert-Signal 类在 “Include\Expert\Signal” 文件夹下提供了许多示例实例，每个实例都可以独立使用，也可在向导中相互组合，搭建一款智能交易系统。至于本文，我们将致力于以智能交易系统的形式创建和使用一个这样的文件。这种方式在把初步编码工作量最小化之外，还允许通过为每个使用的信号分配权重，在单个 EA 中测试一个以上的信号。

Alglib 感知器类在文件 “Include\Math\Alglib\dataanalysis.mqh” 中，并以广泛且相互链接的网络接口呈现。当您第一次看到这些时，很容易不知所措，但我们将在此查看一些关键的类，希望能令该领域易于导航。

使用这些 Alglib 类开发 EA 的主要动机与使用 MQL5 向导相同，即思路测试。我怎样才能简明扼要地判定一个思路 x，或输入数据集 y，是否值得我努力严谨开发，进而成为一款交易系统？我们在此探讨的内容能帮助回答这个问题。

在我们置身其中之前，或许更有帮助的是，更广泛地了解为什么感知器，或许还有神经网络在许多圈子里都普遍收获了大量吸引力。如果我们坚守金融和市场，我们能看到，在预测市场动作方面存在相当多的挑战，而传统分析的局限性也隐含在其中的。

这些挑战之所以存在，是因为市场是一个非常复杂、且往往是动态的系统，其所受影响比新闻（公共信息）中出现的内容更多。 大多时候，各种市场变量之间的关系并非线性的，且十分反复无常。依赖于传统的线性分析方式也许难以有效地捕获和解释这些复杂性。这些传统方法的示例包括像是相关性、PCA、或线性回归等方式。全都是响当当的招数，但越来越多地发现问题超出了自己的深度。除此之外，市场数据本身就很嘈杂，市场走势不仅受到投资者情绪的影响，还受到消费者行为偏差的影响。故而，传统技术分析因依赖历史数据而受到限制，在博弈中难以正确考量所有这些市场动态。像这样在某种程度上存在争议，即基本面分析法权衡内在价值，并取长期视野，而这易遭短期风险，尤其是当它与价格动作有关时。虽然那些依赖基本面分析法的人典型情况不会运用杠杆，但大多数人都会同意它（杠杆）是提升资产管理规模的重要组成部分，故长期存在风险，但亦不能在忽略短期价格动作时使用杠杆。

这两种传统方式的新兴替代者是行为金融学和依据神经网络的人工智能技术。虽然前者结合了心理学和行为经济学的见解来掌握投资者行为，但它是后者的一种适度形式，神经网络，我们将在此详述。

最近，随着 ChatGPT 的推出，金融市场随着人工智能技术的兴起而发生剧变。相当多的主流公司都在权衡，举例彭博社（BloombergGPT） 现在已成形，Sales Force 的 EinsteinGPT 也是如此。今日 GPT 不是此处的主题，但有极度简化的版本，谓之感知器。

尽管如此，人们对人工智能技术进行预测的兴趣日益浓厚，这在一定程度上归因于如今富集的财经大数据。举例，还记得那个所有技术分析师都关心证券每日收盘价的时代吗？好吧，如今每个人都知道典型情况下一分钟柱线的 OHLC 价格是最小时间周期，这是在您谈论即刻报价之前，其频率因经纪商而异。

幸亏芯片供应商之间的良性竞争，这种数据过载与计算能力并驾齐升。昨天，英伟达宣布将很快成为全球最大的芯片供应商，这在很大程度上要归功于 GPU 的需求激增，在于 GPT 现在风靡一时。因此，数据存储的增加和计算能力的提高导致了更多的算法交易。尽管算法交易可由传统的技术分析和基本面分析来完成，但利用神经网络的人工智能技术正越发汇聚更多的光彩。

神经网络倾向于更擅长处理大数据，及识别复杂非线性形态。此外，它们倾向于通过经常所说的深度学习来适应不断变化的环境，这是多层网络的委婉说法，其中特定的隐藏层在特定任务中变得专业化，如此它们在典型的湍流/变化环境中进行预测是一个很好的用途。在金融领域之外，它们可以分析非结构化数据，如新闻文章或社交媒体帖子，测量市场情绪，帮助评估药物临床试验的有效性，以及大量其它案例。

Alglib 感知器类概观

如前所述，Alglib 感知器类层次是一个庞大的类库，它实现了神经网络，从我们在本文中研究的简单感知器一直到融汇，其为转换器的同义词，表示神经网络的堆栈，但由于我们只查看非常基本的神经网络， 谓之感知器，我们将只涉及 “CMLPBase”、“CMLPTrain”、“CMLPTrainer” 和 “CMultilayerPerceptron” 类。还有其它次要的辅助类我们也会用到，例如处理报告的类，或帮助常规化数据集的类，但上面这些才是我们强调的主角。

“CMLPBase” 类用于初始化网络，关键是设置网络所拥有的隐藏层数量，以及每层上的神经元数量。“CMLPTrain” 类初始化训练器类，设置网络所拥有的输入数量，以及输出数量。此外，它还采用训练数据集填充训练器，该数据集应采用矩阵形式，第一列保存自变量，最后一列保存回归器或分类器，具体取决于所用的网络类型。在我们的例子中，它将是一个分类器，因为感知器典型情况提供布尔输出。当调用 “CMLPTrain” 类的 “MLPTrainNetwork” 函数时，“CMLPTrainer” 类用于训练。还有其它一些非常有趣的训练方法，诸如调用函数 “MLPEBaggingLM” 的牵引带汇聚法（boot-strap-aggregating），但这些只能与融汇（网络堆栈）共事。此外，一些算法像是：早期停止、LBFGS、和 Levenberg-Marquadt，也可用于训练网络。

这些类中所用的方法囊括神经网络的典型行程，从加载训练数据，到执行实际训练，最后为以后预测依据当前数据集进行前向验算。

故此，这些类是围绕神经网络的工作进行编码的。在操作中，输入数据向前馈送贯穿网络，从第一层（在这些类中称为输入层）开始，然后馈送到隐藏层，最后馈送到输出层。此外，数值的激活通常在每个神经元上执行，正是这种激活令网络能够处理线性关系之外的复杂关系，充当过滤器，允许选定的数值进入下一层。这个过程是迭代的，但相对直截了当，因为它几乎总是乘法和加法的情况，输出层的结果主要受每一层的权重和乖离的影响。因此，正是这些权重和乖离构成了神经网络的关键，且它们的调整过程不仅在计算上是密集型的，而且导致了不同方式的发展，因为它不像前向验算那么简单，并且没有一种方法可以在各种类型的网络上都能发挥出色，因为神经网络有多种应用。

故此，AlgLib 中网络的前向馈送函数被命名为 “MLPProcess”。它有一些变体，但原则上它从向量或数组中取得输入数据，且典型情况下在输出层，数值通常也保存向量或数组当中。在输出层上存在具有单个神经元的网络，在这些实例中，该函数存在重载，并返回单个数值而非数组。

重点要注意的是，尽管我们正在编码的是使用单个隐藏层的感知器，但我们的参考类称为多层感知器，因为对于任何初始化网络而言，隐藏层的数量是可扩展的，可在运行时设置，且它们的范围从 0 到 2。

如果我们尝试拉近典型前馈的工作，我们可以查看函数 “MLPInternalProcessVector”。该函数的第一个动作工序是规范化输入数据行，以便此输入数组的所有值都更具相关性。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CBdSS::DSNormalize(CMatrixDouble &xy,const int npoints,
                        const int nvars,int &info,CRowDouble &means,
                        CRowDouble &sigmas)
  {
//--- function call
   DSNormalizeC(xy,npoints,nvars,info,means,sigmas);
//--- calculation
   for(int j=0; j<nvars; j++)
     {
      //--- change values
      for(int i=0; i<npoints; i++)
         xy.Set(i,j,(xy.Get(i,j)-means[j])/sigmas[j]);
     }
  }

为了执行此操作，需要使用输入向量中每列的均值和标准差（sigmas）求出 0 – 1 范围内的数值。因此，需要从训练数据集中手工定义均值和 sigmas，然后指派给网络。在同一个 Alglib 文件 “DSNormalize” 中，已经有一些函数可以执行此计算，如以下清单所示：

//+------------------------------------------------------------------+
//| Normalize                                                        |
//+------------------------------------------------------------------+
void CBdSS::DSNormalize(CMatrixDouble &xy,const int npoints,
                        const int nvars,int &info,double &means[],
                        double &sigmas[])
  {
   CRowDouble Means,Sigmas;
   DSNormalize(xy,npoints,nvars,info,Means,Sigmas);
   Means.ToArray(means);
   Sigmas.ToArray(sigmas);
  }

还值得注意的是 “m_structinfo” 数组，存储有关网络的关键信息，例如神经元总数、所用的激活类型、权重总数、输入层中的神经元数量，以及输出层中的神经元数量。

常规化之后，数据馈送至网络，每层上的每个神经元都能够拥有自己的激活函数。这种定制化可以由函数 “MLPSetNeuronInfo” 来定义，在构建网络中可轻易地利用其作为优势。

与训练相比，前向馈送感知器相对简单，只是调整网络权重。Alglib 主要提供 2 种训练方式，即 Levenberg Marquadt 和 LBFGS。

在寻求非线性最小二乘解时，Levenberg Marquadt 算法将高斯-牛顿算法的速度、梯度下降算法在求解高曲率点的灵巧性结合在一起。这样做时，它使用 黑森（Hessian） 矩阵来记录曲面的曲率，从而估算它到达解值有多近。它主要应用在神经网络当中，其中可有效地处理非凸起误差表面，特别是涉及小型数据集的状况下，相对简单网络架构更给力，因为计算黑森矩阵是重赋。

另一方面，LBFGS 立足于有限内存 Broyden-Fletcher-Goldfarb-Shanno 算法，它并非计算黑森矩阵，而是通过记录最新的网络权重更新，以有限的内存来近似它，令其在计算和内存各方面极其高效。由此，它更适合大数据状况，及相对复杂的网络架构。

话虽如此，两者的收敛特性倾向偏于 Levenberg Marquadt，因为它能快速收敛到精确解，即使在初始猜测其路不通的状况下（就像网络用随机权重初始化时）。外加它不太容易卡在局部最小值，像是梯度下降，令其更加稳健，归因于部分用到 lambda 阻尼因子。另一方面，LBFGS 必然会受到初始猜测（在我们的例中为初始网络权重）的影响更大，并且必然会收敛得更慢、或卡在局部最小值。

编码智能信号类的实例

据针对感知器工作的简要介绍，更多阅读和参考资料可以在此处找到，我们可以开始查看实例编码。使用 MQL5 向导创建新的智能交易系统的过程，需要领悟定义基于向导的智能交易系统的 3 个典型类，即我们本文重点关注的信号类、指导如何设置持仓止损的尾随类，以及有助于设置交易手数的资金管理类。这在之前的文章中都已接触过。在组装期间，这三个全部都需要在向导中定义和选择。尽管资金管理类提供了规模优化的交易量，但某些情况下也可考虑额外的第 4个向导类，该类着眼于风险，智能系统在单笔持仓中下多笔订单的安全性如何，这也可以基于交易历史或某些指标，但其尚不可用，故不予考虑。

为了实现 Alglib 感知器类的实例，并作为单层感知器，我们首先要在自定义智能系统信号类的接口中声明我们的关键类实例。信号类文件总会含有 “LongCondition”和“ShortCondition” 函数，我们将添加的额外函数，帮助计算或处理来自感知器的信号，这是除了初始化和验证函数之外我们唯一需要的其它关键方法。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalPerceptron          : public CExpertSignal
  {
protected:
   
   int                           m_hidden;                              // 
   int                           m_features;                            // 
   int                           m_hidden_1_size;                       //
   int                           m_hidden_2_size;                       //  
   int                           m_training_points;                     //
   int                           m_training_restarts;                   //
   int                           m_activation_type;                     // 
   double                        m_hidden_1_bias;                       //
   double                        m_hidden_2_bias;                       //
   double                        m_output_bias;                         //

public:

...

protected:

   CBdSS                         m_norm;
   CMLPBase                      m_base;
   CMLPTrain                     m_train;
   CMatrixDouble                 m_xy;
   CMLPReport                    m_report;
   CMLPTrainer                   m_trainer;
   CMultilayerPerceptron         m_network;
   
   bool                          m_in_training;
      
   int                           m_inputs;
   int                           m_outputs;
   
   double                        m_last_long_y;
   double                        m_last_short_y;
   
   bool                          ReadWeights();
   bool                          WriteWeights(CRowDouble &Export);
   
   void                          Process(double &Y);
  };

在智能系统信号类实例当中，验证函数是事实上的初始化函数，是的，虽有一个内置的初始化函数，但验证函数可为我们更好地服务。其内有几件必须要完成的事情值得一览。首先，我们为感知器指派输入和输出的数量。输入数量将是可优化的，故此要从参数中读取，但输出数量，因为这是一个分类而非回归，所以必须至少为 2。

末了，出于简单起见，我们将为输出指派 2。然后，我们调整训练数据矩阵的大小，令其行数与我们在处理方向时每根柱线上所取训练点数相匹配。其列数应与输入和输出数量的合计相匹配。输出为 2，代表训练时看涨和看跌的两个权重，事实上，向前验算同样会返回两个概率，一个是做多，另一个是做空，两者加起来为 1。此后，我们创建一个训练器，并设置其输入和输出的数量。

   m_train.MLPCreateTrainerCls(m_inputs,m_outputs,m_trainer);

随后是网络的创建，根据所选隐藏层的数量，我们将调用不同的函数来达成这一点，每个函数都允许定义输入神经元的数量、每个隐藏层中的神经元数量（如果用到它们）、最后是输出层中的神经元数量。

   if(m_hidden==0)
   {
      m_base.MLPCreateC0(m_inputs,m_outputs,m_network);
   }
   else if(m_hidden==1)
   {
      m_base.MLPCreateC1(m_inputs,m_hidden_1_size,m_outputs,m_network);
   }
   else if(m_hidden==2)
   {
      m_base.MLPCreateC2(m_inputs,m_hidden_1_size,m_hidden_2_size,m_outputs,m_network);
   }
   else if(m_hidden>2||m_hidden<0)
   {
      printf(__FUNCSIG__+" invalid number of hidden layers should be 0, 1, or 2. ");
      return(false);
   }

最后结束，我们设置隐藏层和输出层激活函数，以及层乖离。Alglib 类的功用相当全面，如激活函数和乖离不仅可以针对每一层进行定制，实际上能针对每个神经元。只是对于本文，我们正在寻找一些简化的东西。

除了初始化和验证我们的网络外，我们还需要有适当的规定，通过填充系统，并在需要时读取它们来学习网络的理想权重。此处有许多不同的方式可以考虑，但我们要用的只是在测试通过后，挑出其中超过之前基准的 EA 测试准则，把其网络权重数组写入文件。在下一次运行时，我们的网络初始化时读取这些权重，且随着每次成功的训练，它们会得到改进。将权重写入文件、及其读取，分别由 “WriteWeights” 和 “ReadWeights” 函数完成。

最后，“Process” 函数在每根新柱线上执行，用新数据训练我们的网络，然后处理当前信号，其引用变量 “Y”。此处有几件事值得注意：首先，测试数据矩阵 “m_xy” 需要按列进行常规化，以便矩阵中的每个值都在 -1.0 至 +1.0 的范围内。如上所述，这可以调用 Alglib 类中的其它函数来完成，它们与感知器类来自同一个文件。当然，人们可以自定义这种方式，以便令其更适合他们的状况，但对于我们的目的，将使用内置函数。

      //normalise data
      CRowDouble _means,_sigmas;
      m_norm.DSNormalize(m_xy,m_training_points,m_inputs,_info,_means,_sigmas);

其次，网络的训练由两个函数完成，具体取决于我们是刚刚开始训练过程、亦或已经执行过训练。一旦我们开始训练，为免再次处理随机权重，我们就可以保留从前次验算学到的权重，并继续训练。默认的训练函数总是随机化权重，如果我们要使用它，我们将在每根新柱线上随机化我们的权重！

      m_train.MLPSetDataset(m_trainer,m_xy,m_training_points);
      //
      if(!m_in_training)
      {
         m_train.MLPStartTraining(m_trainer,m_network,false);
         m_in_training=true;
      }
      else if(m_in_training)
      {
         while(m_train.MLPContinueTraining(m_trainer,m_network))
         {
            //
         }
      }

好在有向导，将完整的信号类、尾随类、和资金管理类，无缝集成到一款智能系统当中。

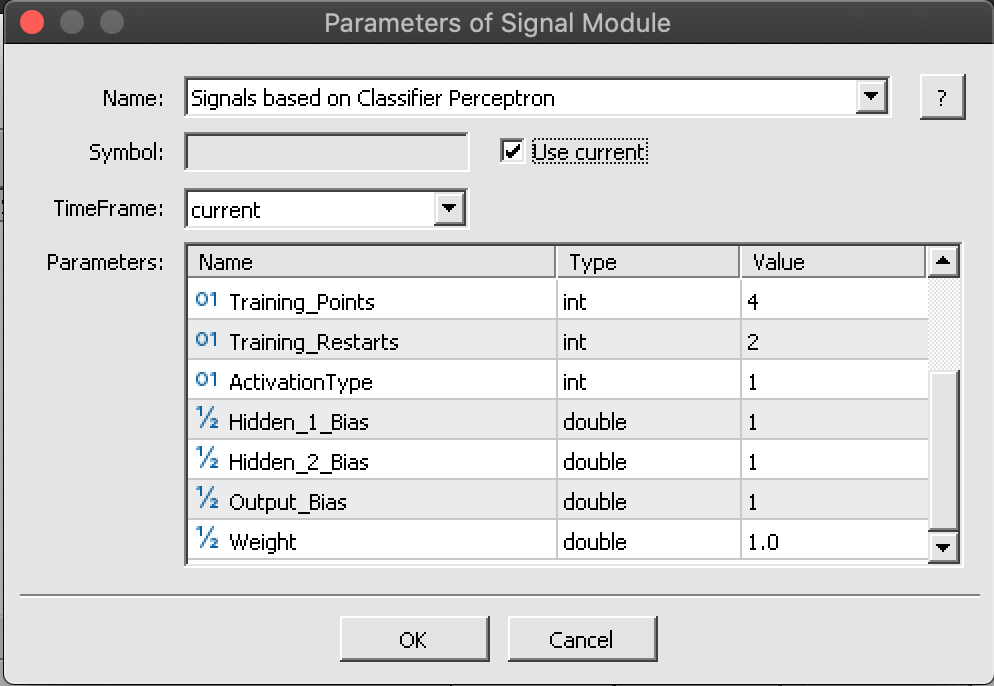
<images: 向导中组装的 7 个步骤/>

如果我们按照上面 7 张图片中高亮显示的 7 个步骤进行操作，我们最终会得到一款智能系统，其包含头文件如下所示：

//+------------------------------------------------------------------+
//| Include                                                          |
//+------------------------------------------------------------------+
#include <Expert\Expert.mqh>
//--- available signals
#include <Expert\Signal\My\SignalPerceptron.mqh>
//--- available trailing
#include <Expert\Trailing\TrailingNone.mqh>
//--- available money management
#include <Expert\Money\MoneyFixedMargin.mqh>

组装和测试 EA

由此，由向导直截了当地将我们的自定义智能信号类组合成一款智能系统，如上面的屏幕截图所示。

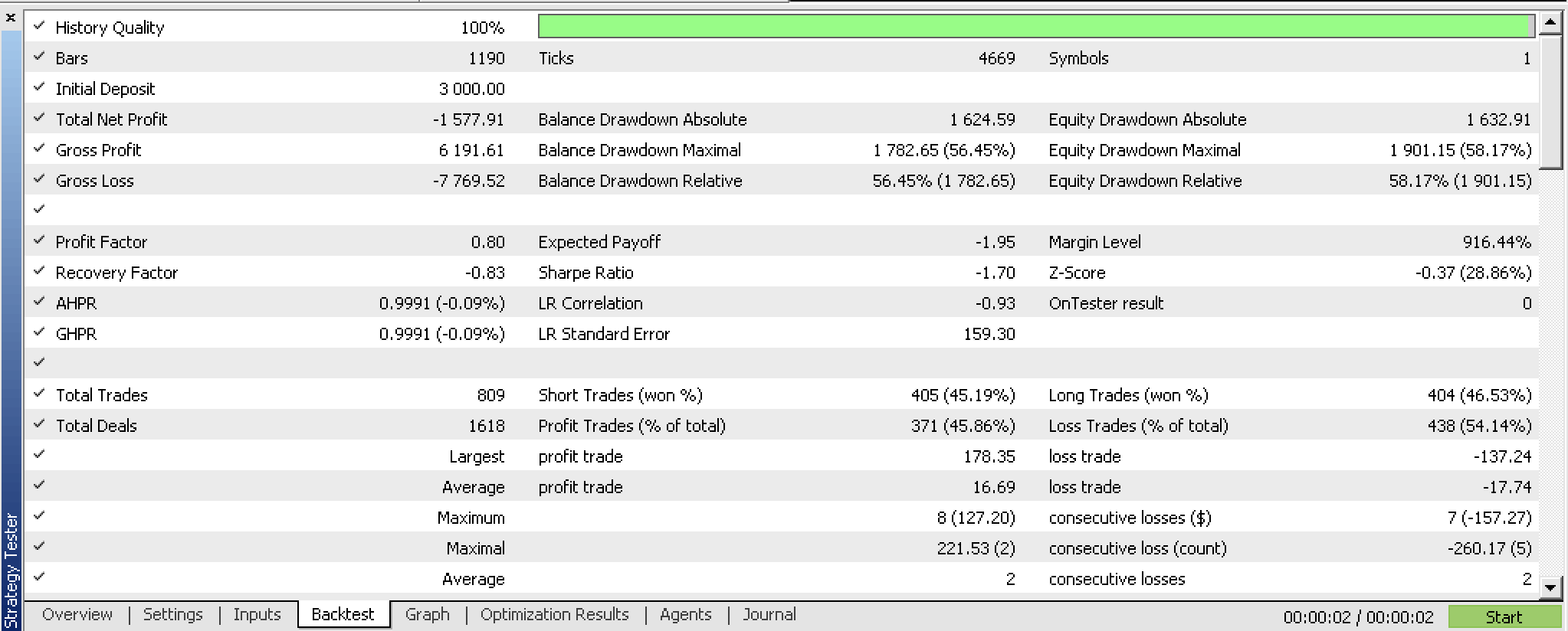
如果我们在进行任何优化之前，针对编译过的智能系统进行回溯测试，我们会得到以下报告：

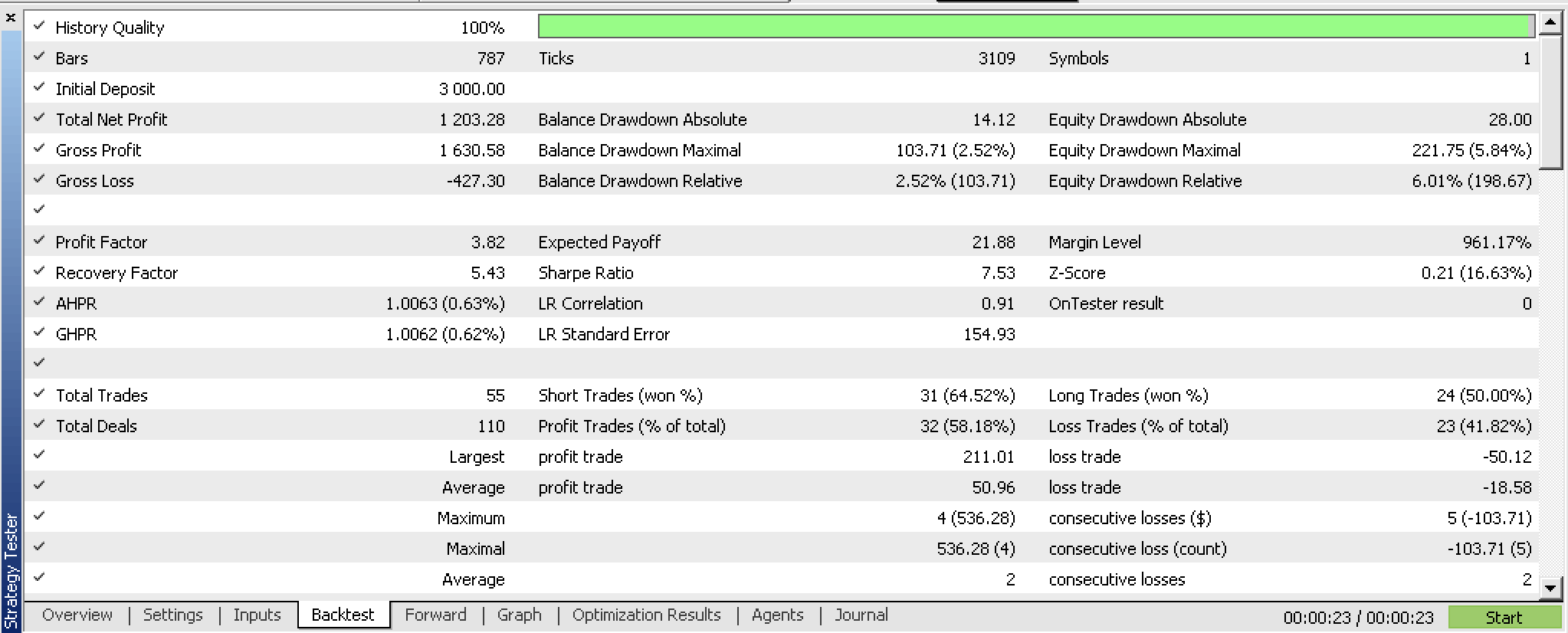
如果我们执行智能系统优化时，采用一个向前漫游的窗口 ，会得到以下结果：

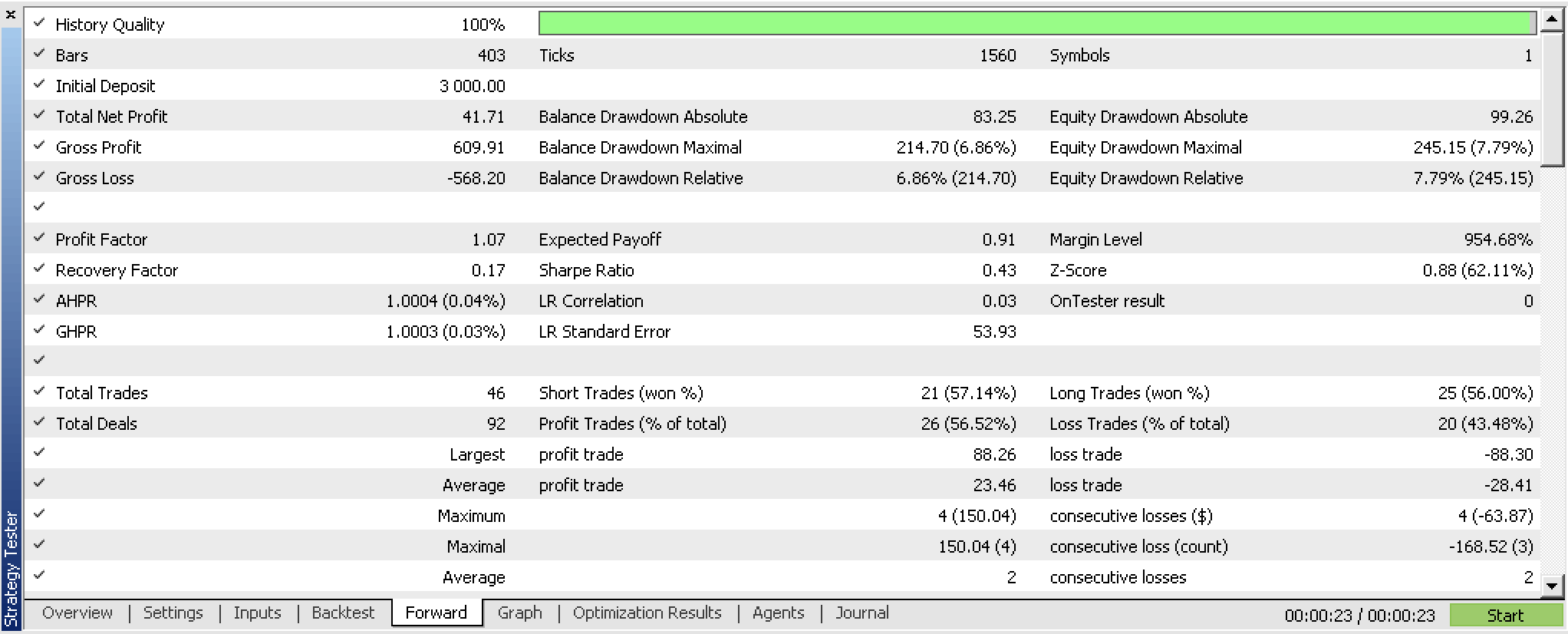
我们已经训练过我们的感知器，并基于我们的智能系统的优化准则导出了它的权重。一种更简洁的方式是使用内置的交叉验证能力，或者如果未使用装袋，就可采用比较简单的东西，像是报告的均方根误差值。无论哪种场景，我们都可以存储更有可能与训练分类器匹配的权重。据我们的测试，该网络展现出一定前景，但如常，在依据经纪商的即刻报价数据进行更长时间的测试时要参考其它因素，这一点应牢记。

结束语

总而言之，我们已经看到，幸好有 Alglib 代码类，用户如何以最少的代码实现感知器。我们已经强调了一些初步步骤，像是数据集常规化，前器需要采取这些步骤，这样感知器才值得测试和从中学习。此外，一旦您准备好测试感知器，我们还展示了值得参考的额外措施。所有这些步骤和额外措施，如可调参数的导出，都是由 Alglib 类的辅助代码完成的。

故此，使用 Alglib 类的优点主要是最大限度地减少代码量，以及测试系统所花费的时间。但这也有少量缺点，尤其是在定制方面。举例，我们的感知器不能超过 2 个隐藏层。在对复杂数据集进行建模的场景，这将是一个瓶颈。