Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
Sorento :
Başka? Sonuçta daha fazlası gerekiyor. :)
Eh, Tanrı onun için, kesinlikle çok katı! Kabul ediyorum.
Yönteminize göre değerlendirin ve sonucu sunun.
{ N =120, q (ay)=%60,91/12 Başlangıç Sermayesi=100 } koşulları altında grafikte gösterdim. ve K ile şamanlaşmak - Bunu yapamam. .
Birisi bu koşullar için kOpt verirse - sayı sonrası tabloları çizeceğim ve yuvarlamayı hesaba katacağım ...
;)
Şimdi, Matematikçi ve Sorento için bir soru: yukarıda, ikiniz de eşsiz Mikhail Andreevich'in çözümüne atıfta bulundunuz - Peki şimdi ne olacak? her şey açık ... gibi - sırada ne var?
Saygın Mikhail Andreevich'in hesabın iki katına çıkma süresi için kutsal formülden başka bir şeye sahip olmadığı ortaya çıktı, hiçbir şey :-) Genel olarak, sanırım, Alesei'den kOpt için yaklaşık bir çözüm bekliyoruz.
Şimdi Matematikçi ve Sorento için bir soru: yukarıda, ikiniz de eşsiz Mikhail Andreevich'in çözümüne atıfta bulundunuz - Peki şimdi ne olacak? her şey açık ... gibi - sırada ne var?
Saygın Mikhail Andreevich'in hesabın iki katına çıkma süresi için kutsal formülden başka bir şeye sahip olmadığı ortaya çıktı, hiçbir şey :-) Genel olarak, sanırım, Alesei'den kOpt için yaklaşık bir çözüm bekliyoruz.
Meraklı sonuç.
Topt süresinden önce herhangi bir (orantılı dahil) geri çekmeyi içeren stratejiler optimal değildir ... Depo süresinin TT'den fazla olması şartıyla - doğal olarak.
Lütfen resme bir göz atın (sayısal)...
;)
Görünüşe göre biraz farklı bir problemi (daha karmaşık) çözmeye başladık.
Hatırlatmama izin verin, koşula göre, kullanımda olan t zamanı için, mevcut mevduat tutarının sabit bir yüzdesi q aylık olarak tahakkuk eden bir mevduatım var ve q'dan fazla olmayan sabit bir yüzde k çekmem GEREKİR ve her ay en az %0. Her şey.
Mevduattaki fonları hesaba katmadan t döneminde çekilen fonları maksimize eden böyle bir kOpt bulmamız gerekiyor. Bu çözüm, analitik biçimde iki parametrenin ( q ve t ) bir fonksiyonu olarak temsil edilmelidir (sayısal çözümler, çeşitli grafikler ve bağımlılıklar biçimindeki özel çözümler, zaten elde edildikleri için ilgi çekici değildir). Analitik çözüm yaklaşık ise, sorunun çözümünün beyan edilen doğruluğunun elde edildiği q ve t sınırları belirtilmelidir.
PS Türün tüm özellikleri - tahakkuk eden faizin q sabitliğini değil, k parametresindeki değişiklikleri değil, enflasyonu hesaba katar. En basit durum için bir çözüm elde etmeden önce düşünmenin bir anlamı olmadığını düşünüyorum.
"Size hatırlatmama izin verin, koşula göre, kullanımda olan t zamanı için aylık olarak geçerli mevduat tutarının sabit bir yüzdesi q olan bir mevduatım var ve q'dan fazla olmayan sabit bir yüzde k çekmem GEREKİR ve her ay en az %0."
.
Sergey, ancak formül çok basit olmasa da oldukça görünür olmasına rağmen, sorunun zaten bir cevabı var. Bu gibi durumlarda cevap genellikle referans kitaplarında nomogram şeklinde verilir.
sorunun açıklamalarından açıkça anlaşılıyor: " q 0.1< q <0.3 içinde yatıyor"
Daha fazla "zaman t " aralığı belirtin
Oleg , Forex ile ilgili olarak, t 50'ye eşit olarak ayarlanabilir. Daha az mantıklı değil çünkü 5 yıldan az tipik bir mevduat ömrü ile , tüm kârın çekilmesi doğru olur ve ilk mevduatın büyüklüğü faiz açısından "ömür boyu" sağlamalıdır. Kullanım ömrü 5 yıldan fazlaysa, ilk depozito miktarı göreve dahil değildir ve 1000 ruble'den başlayabilirsiniz. ancak optimal bir para çekme yüzdesi vardır. Ayrıca, karakteristik ömrünün zorunlu bir değer olmadığını hesaba katarsak (istatistiklerden bahsediyoruz), bu parametre sabit = 50'ye ayarlanarak formülden çıkarılabilir. Bu nedenle, (ideal olarak) kOpt için sadece bir parametrenin analitik yaklaşık değerine sahibiz - TS - q'nin ortalama karlılığı.
kOpt=q için t<50
t>50 için kOpt=F(q)
Bulmak istediğim şey, belirtilen koşullar altında F (q) analitik bağımlılığının yaklaşık bir biçimidir.
Formülü nasıl basitleştireceğimi henüz bilmiyorum. Newton'un yöntemi , en azından üçüncü veya dördüncü yinelemeden az çok doğru bir çözüm verir. Çok hantal, çok katlı bir formül olduğu ortaya çıkacak.
q'nun açıklığa kavuşturulması şimdi ayrıca iki terimli genişlemenin burada işe yaramaz olduğunu doğrulamaktadır: q = 0.1 ve t = 10 ile bile, binomun çok fazla terimi korunmalıdır. Ve ne kadar çok t ve q , o kadar kötü. Başka bir deyişle, makul t (muhtemelen 20'den az değil) için hemen hemen her zaman
(1+ qk )^ t ~ exp(( qk ) t )
Gözlemler, büyük q ve küçük t için (örneğin, sırasıyla 0,3 ve 10), aylık kazançların çoğunu ( %70) çekmenin optimal olduğunu söylüyor.
Küçük q ve küçük t için makul bir aralıkta ekstremum yoktur: Kazanılan her şeyi geri çekmeniz gerekir.
Aynı zamanda, ortalama q ve ortalama t (0,2 ve 20) ile, kazanılanın önemli bir bölümünü, yaklaşık yarısını (% 44) çekmek mantıklıdır.
Ayrıca, orta q ve büyük t (0,2 ve 30) için kazançların daha küçük bir kısmını (%26) çekmek mantıklıdır.
Vb. vb. Görev, farklı parametreler için niteliksel olarak farklı davranır. İyimser, tek bir cevap yok gibi görünüyor. Belki q ve t'ye bağlı olarak bir k tahmini yapmaya çalışın?
Not: Yorumunu görüyorum, Sergey . Tamam, t =50'yi düzeltin. Görev daha kolay hale geldi: Kazanılan paranın daha küçük bir kısmını çekmek yeterli ( q = 0.1, t = 50 -> k / q = 0.3, yani %30). Bu, mümkün olan maksimum k / q'dir .
.................
.................
................
Alfa'nın optimal değeri, pozitif bölgeden negatif bölgeye geçişe karşılık gelir.
.
Formül yukarıda verildi, burada tekrar edeceğim
Matkad'da çoğaltmanız zor olmayacak --- parametreleri hızlı bir şekilde seçebilirsiniz.
(ve bir rol oynamaz)
Belki q ve t'ye bağlı olarak bir k tahmini yapmaya çalışın?
O zaman analitik çözümün zarafeti kaybolur. Bu durumda sayısal çözümü kullanmak daha doğrudur. Sorun basit bir ifade için çok zor gibi görünüyor ...
Çekilen para miktarı için orijinal ifadeyi basitleştirmeye çalıştım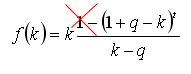 .
.
Bu durumda, k parametresine göre birinci türevin genel formu, basit bir ikinci dereceden denkleme kadar büyük ölçüde basitleştirilmiştir:
Bunu çözerek, yaklaşık bir ifade elde edilebilir.
t >50, q >0.1 aralığında kabul edilebilir doğrulukla
Daha fazlasını istedi...