kiracı - sayfa 6
Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
Hayır hayır. yanılmıyorum. Burada, yinelemeli formülden (kırmızı) ve analitik bağımlılıktan (mavi) çıkan, çekilen para miktarının bağımlılığıdır.
Çakıştıkları ve k cinsinden bir maksimum olduğu görülebilir (konunun bir önceki sayfasında).
Açıkçası, ayrı bir para çekme işleminiz yok, ancak eşit paylarda sürekli bir geri çekilmeniz var. Bu nedenle farklı dönemlerde farklı şekillerde çekim yapma kararınız yoktur. Bu nedenle, daha önce çıkarmadan sonunda her şeyi kaldırmanın bir çözümü yoktur. Bu, sorunun koşullarından değil, kullandığınız formüllerden kaynaklanır (k sabittir, ki değişkeni değil, i=0...T)
Çekilen toplam para
etki, yeterince büyük bir büyüme faktöründe fark edilir hale gelir
Benzer bağımlılıklarım var.
Şimdi türev ifadesini k'nin kuvvetleriyle genişletmeye çalışıyorum, ama bundan iyi bir şey çıkmıyor - en fazla altı sıra tutmam gerekiyor. Bunun analitik olarak çözülemeyeceği açıktır. Belki daha fazla fikir vardır? Birisi difurki'den bahsetti ...
Benzer bağımlılıklarım var.
Şimdi türev ifadesini k'nin kuvvetleriyle genişletmeye çalışıyorum, ama bundan iyi bir şey gelmiyor - altıya kadar sıralama tutmam gerekiyor. Bunun analitik olarak çözülemeyeceği açıktır. Belki daha fazla fikir vardır? Birisi difurki'den bahsetti ...
analitik olarak zor. q ve t'den. Bir şekilde zor bağlıdır :) q arttıkça, t'de olduğu gibi, optimal geri çekilme oranı sürekli olarak azalır
Benzer bağımlılıklarım var.
Şimdi türev ifadesini k'nin kuvvetleriyle genişletmeye çalışıyorum, ama bundan iyi bir şey gelmiyor - altıya kadar sıralama tutmam gerekiyor. Bunun analitik olarak çözülemeyeceği açıktır. Belki daha fazla fikir vardır? Birisi difurki'den bahsetti ...
Özelden genele gidebilirsiniz. Örneğin, t = 1 ise, sadece bir kez para çekebilirsiniz ve bu nedenle q miktarında para çekmeniz gerekir. Daha sonra, t = 2, t = 3 vb. için durumu ele alıyoruz.
Onlar. Eğer t = 2'de bir seferde q'dan daha az çıktı almak optimal ise, o zaman ekstremumu bulun ve t = 2'de tüm q'lar için genelleyin.
Benzer şekilde t = 3, t = 4, vb.
Ekstremin değeri ile para çekme miktarını f(t) olarak almak mümkün olacaktır.
Kontrolü hazırlamak için bağlı gemilerin bir şemasını düşünebilirsiniz.
Birinci kabın başlangıç hacmi B0
Özelden genele gidebilirsiniz. Örneğin, t = 1 ise, sadece bir kez para çekebilirsiniz ve bu nedenle q miktarında para çekmeniz gerekir. Daha sonra, t = 2, t = 3 vb. için durumu ele alıyoruz.
Ekstremin değeri ile para çekme miktarını f(t) olarak almak mümkün olacaktır.
Belki de haklısın. Sadece şimdi t =3 için denkleme göre elimizde
k derecesi birinci türev df(k)/dk=0 'da bir üçlüdür ve tüm sonuçlarıyla birlikte kübik denklemin köklerini aramamız gerekir... Yani. t =3'ün ötesinde bu senaryoyu geçemeyiz. sana şunu hatırlatmama izin ver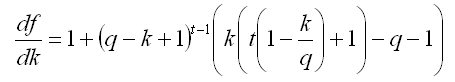 
, ve t=1 için optimal boyut k=q, t=2 için k=q, t=3 için k=q'dur. Ancak t'yi daha da artırmak ve analitik olarak çözmek işe yaramaz. Sayısal olarak çözersek, ayda %10'luk bir mevduat büyüme oranı q için, hesaptan optimal para çekme yüzdesinin t > 30 ayda q'dan daha az olduğu görülebilir.
Bundan çıkan sonuç şudur: TS'nin güvenilirliği , mevduatın ortalama ömrü 3 yılı aşmayacak şekilde ise, o zaman tüm karların aylık olarak çekilmesi optimal davranış olacaktır (mevduat büyümez). Aksi takdirde, optimal çıktı yüzdesi k için analitik bir çözüm aramanız ve formüle göre hareket etmeniz gerekir. Bu senaryo, mevduatın beklenen ömrü boyunca cebe konan maksimum para miktarını garanti eder.
otomatik :
PS'yi hazırlamak için, bağlı kapların bir diyagramını düşünebilirsiniz.İlk kabın ilk hacmi B0'dır.
Kaplar (sıvı akışı) dinamik dengedeyse (yani, birinci kaba birim zamanda ne kadar sıvı akar, ikinciden aynı miktarda sıvı akar), her kaptaki su seviyesi sorunu temel olarak çözülür ve mevduatın belirlenen sorununa indirgememek. Kapları doldurma sürecinde düşünürsek, depozito ile benzerlik tam olarak açık değildir. avtomat , açıkla , lütfen, böyle bir yorum sunmakla ne demek istediniz?
PS df/dk=0 denkleminin yaklaşık bir analitik çözümünü elde etme çağrısı yürürlükte kalır. Herhangi bir fikir kabul edilir.