Alım-satım fırsatlarını kaçırıyorsunuz:
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Kayıt
Giriş yap
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Hesabınız yoksa, lütfen kaydolun
Ve bu kanıtlayıcı "bilimsel imgelem" daha ne kadar devam edecek?
Son akor nerede?
Hayat dolu final!
;)
Bana öyle geliyor ki, kübik bir denklemle bile, büyük t için yaklaşıklık yine de kaba olacak. Evet ve Cardano formülüyle ya da Vieta'nın ortalığı karıştırmasıyla eziyet çekeceksin, Sergey ...
Ne yaptım: (1+qk)^t = (1+epsilon)^t'yi iki terimli olarak üçüncü kuvvete genişlettim. q = 0.01 ve dolayısıyla epsilon <~ 0.01 olduğunu varsayın.
t=50 diyelim. Sonra hesap makinesinde (1+0.01)^50 = 1.645. 3. kuvvete binom yaklaşımı: (1+0.01)^50 ~ 1 + 50*0.01 + 50*49/2*0.01^2 + 50*49*48/6*0.01^3 = 1 + 0.5 + 0.1225 + 0.0196 = 1.6421. Evet, oldukça doğru.
Ama diyelim ki, t=100'de (8 yıldan biraz fazla), kesin sonuç 2.7048... (bu arada neredeyse e sayısı). 3. güce binom yaklaşımı bize 1 + 100*0.01 + 100*99/2*0.01^2 + 100*99*98/6*0.01^3 = 1 + 1 + 0.495 + 0.1617 = 2.6567 verir. Artık çok doğru değil ve t büyüdükçe hata da büyüyecek.
Kısacası, büyük t'de, binomun herhangi bir kesilmesi sistematik bir hata vermeye başlar. Bana öyle geliyor ki, bir şövalye hamlesi yapmak - iki terimli açılımları terk etmek ve basitçe Newton'un yöntemiyle çalışmak mantıklı görünüyor. Belirli koşullar altında ardışık yaklaşımlar çok hızlı bir şekilde tam değere yakınsar ve aşağıdaki gibi hesaplanır (denklem f(x)=0):
x(n+1) = x(n) - f(x(n))/f'(x(n))
f'miz çekilen fon miktarının birinci türevi olduğu için ikinci türevini bulmamız gerekecek. Formül hantal olsa da teknik bir sorun olmamalıdır. Biraz sonra yayınlayacağım.
2 avtomat: beni bile kes, ama kafes işleviniz ile epsilon'un küçüklüğü arasında herhangi bir bağlantı görmüyorum (bu değişken temelde süreklidir). Sonunda süreç kontrol sisteminizi çözen formülü gösterebilir misiniz? :) Bir önceki sayfada Neutron'un verdiği formülden bahsediyorum.
Enerjin pilimde olsun. Hımm....
Birinin yapacak özel bir şeyi yoksa ve gerçekten zihinsel enerjiyi bir şeye uygulamak istiyorsa, Gilbert-Huang dönüşümlerini C++'dan MQL4/MQL5'e yeniden yazarak topluma fayda sağlayabilir. Ekli kod.
Yani, burada bir şey ortaya çıktı ve tekrar kayboldu. Tamam, hala Newton tanjantlarıyla çözüyorum. Ve tüm süreç kontrol sistemleri ve yıllıklar umurumda değil :)
ASUTP ve seni bekliyorum. Sonra çıldırırım...
;)
yanlış başlangıç - ticari bileşeni değerlendirmek için nuno.
Aksi takdirde, tekrar bitki mi?
DDD
https://ru.wikipedia.org/wiki/%D0%90%D0%BD%D0%BD%D1%83%D0%B8%D1%82%D0%B5%D1%82 - çok net değil ama "postnumerando annuity" ifadesini gerçekten beğendim.
Her akşam oral seks yapmakla aynı şey :)
Aleksey, "dost ya da düşman"ın sabit oranındaki kuruntu hakkında haklı olarak belirtti.
Ama sonra, her zamanki gibi, iyimser bir çıkmaza girdi.
Böyle.
Birinin gerçekten bir çözüme ihtiyacı varsa, vizyonumu yayınlarım. (Arşimet banyolarında beklemek için proses kontrol sistemlerinden bıktım;)
İlk olarak, tahakkuk eden tüm faizleri geri çekmeme tekniğini kullanma olasılığına karar vermelisiniz.
Bunun için mevduat süresinin sonuna kadar olan sürenin kesinlikle daha büyük olması gerektiğini anlamak kolaydır.
Sonucu L olarak kabul ediyoruz
daha sonra da basitçe görüntülenir (mevduatın maksimum "verimli" alanını / boyutunu hatırlayarak -;)Sp düz bir çizgi olarak tanımlanır -
Sonuç olarak, maksimum para çekme limitimiz var. Sr, birikim payıdır...
davranışlarının programı -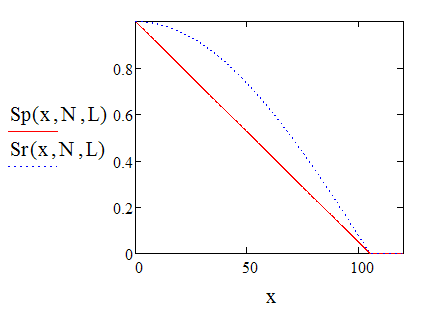
Sadece okuyun ve kullanın.
- Do=100, N=12*10 A STAFKA için örnekler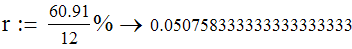
Ve yıllık gelir benim için söz konusu ve eğer onun formülünü de kendim türetmeye çalışsaydım.
B mevduattan tahakkuk eden faizin çekilme tutarının dahil olduğunu not ediyorum. N, L'den küçükse.
;)
Son çizimin "kavramsal" olduğunu not ediyorum ...
NASIL ispat fikrini anlamak için.
Herkes sadık bir tane inşa edebilir ve şaşırabilir.
;)
Örneğin, q=0.01 (ayda %1) ve t=80'de k neye eşittir?
Dürüst olmak gerekirse, kosinüslerin gergin, Mikhail Andreevich . Black-Scholes formülüne aşina olmasaydım, o zaman bir tortuya düşerdim ...
Örneğin, q=0.01 (ayda %1) ve t=80'de k neye eşittir?
Dürüst olmak gerekirse, kosinüslerin gergin, Mikhail Andreevich . Black-Scholes formülüne aşina olmasaydım, o zaman bir tortuya düşerdim ...
sinüse geç...
D
:)