MetaTrader 5 / İstatistik ve analiz
English Русский 中文 Español Deutsch 日本語 Português 한국어 Français Italiano
Box-Cox Dönüşümü

Box-Cox Dönüşümü

MetaTrader 5 — İstatistik ve analiz | 22 Aralık 2021, 14:30
678 0
Victor
Victor

Giriş

Bilgisayar kapasiteleri artarken, Forex yatırımcıları ve analistleri, önemli bilgi işlem kaynakları gerektiren oldukça gelişmiş ve karmaşık matematiksel algoritmaları kullanmak için daha fazla olanaklara sahiptir. Ancak bilgisayar kaynaklarının yeterliliği, yatırımcıların sorunlarını tek başına çözemez. Piyasa fiyatlarını analiz etmek için verimli algoritmalar da gereklidir.

Şu anda, matematiksel istatistik, ekonomi ve ekonometri gibi alanlar, yatırımcılar tarafından piyasa analizi için aktif olarak kullanılan çok sayıda yöntem, model ve iyi işleyen, etkili algoritmalar sunmaktadır. Çoğu zaman bunlar, araştırılan dizilerin kararlılığı ve dağılım yasalarının normalliği varsayımıyla oluşturulan standart parametrik yöntemlerdir.

Ancak Forex fiyat tekliflerinin, istikrarlı ve normal dağılım yasasına sahip olarak sınıflandırılamayacak diziler olduğu bir sır değildir. Bu nedenle, fiyat tekliflerini analiz ederken "standart" parametrik matematiksel istatistik, ekonometri vb. yöntemleri kullanamayız.

"Box-Cox Transformation and the Illusion of Macroeconomic Series "Normality" [1] adlı makalesinde A.N. Porunov şunları dile getirmiştir: 

"Ekonomik analistler genellikle şu veya bu nedenle normallik testini geçemeyen istatistiksel verilerle uğraşmak zorunda kalırlar. Bu durumda iki seçenek vardır: Ya makul miktarda matematik eğitimi gerektiren parametrik olmayan yöntemlere yönelmek ya da orijinal "anormal istatistikleri" "normal" olana dönüştürmeye olanak tanıyan özel teknikler kullanmak; bu da oldukça karmaşık bir görevdir".

A.N.Porunov'un fiyat teklifinin ekonomik analistlere atıfta bulunmasına rağmen, "anormal" Forex fiyat tekliflerini matematiksel istatistik ve ekonometrinin parametrik yöntemlerini kullanarak analiz etme girişimlerine tamamen atfedilebilir. Bu yöntemlerin büyük çoğunluğu normal dağılım yasasına sahip dizileri analiz etmek için geliştirilmiştir. Ancak çoğu durumda, ilk verilerin "anormalliği" gerçeği basitçe göz ardı edilir. Ayrıca, bahsedilen yöntemler genellikle yalnızca normal bir dağılım değil, aynı zamanda başlangıç dizileri durağanlığı gerektirir.

Regresyon, yayılım (ANOVA) ve diğer bazı analiz türleri, ilk veri normalliği gerektiren "standart" yöntemler olarak adlandırılabilir. Dağılım yasası normalliği ile ilgili sınırlamaları olan tüm parametrik yöntemleri, parametrik olmayan yöntemler dışında, örneğin ekonometrinin tüm alanını kapladığı için listelemek mümkün değildir.

Açık konuşmak gerekirse, "standart" parametrik yöntemlerin, ilk veri dağılım yasasının normal değerden sapmasına karşı farklı hassasiyete sahip olduğu eklenmelidir. Bu nedenle, bu tür yöntemlerin kullanımı sırasında "normallikten" sapma, mutlaka korkunç sonuçlara yol açmaz, ancak elbette elde edilen sonuçların doğruluğunu ve güvenilirliğini artırmaz.

Tüm bunlar, fiyat tekliflerini analiz etmek ve tahmin etmek için parametrik olmayan yöntemlere geçmenin gerekliliği sorusunu gündeme getiriyor. Ancak, parametrik yöntemler çok çekici olmaya devam etmektedir. Bu, yaygınlıkları ve yeterli miktarda veri, hazır algoritmalar ve uygulama örnekleri ile açıklanabilir. Bu yöntemleri doğru bir şekilde kullanmak için, başlangıç dizileriyle bağlantılı en az iki sorunun üstesinden gelmek gerekir – istikrarsızlık ve "anormallik".

Başlangıç dizilerinin kararlılığını etkileyemesek de dağılım yasalarını normal olana yaklaştırmaya çalışabiliriz. Bu sorunu çözmek için çeşitli dönüşümler vardır. Bunlardan en bilinenleri kısaca "Box-Cox Dönüşümü Tekniğinin Ekonomik ve İstatistiksel Analizlerde Kullanımı" başlıklı makalede [2] kısaca açıklanmıştır. Bu makalede bunlardan yalnızca birini ele alacağız – Box-Cox dönüşümü [1], [2], [3].

Burada, Box-Cox dönüşümünün kullanımının, diğer tüm dönüşüm türleri gibi, yalnızca ilk dizi dağılım yasasını normal olana az ya da çok yaklaştırabileceğini vurgulamamız gerekir. Bu, bu dönüşümün kullanılmasının, elde edilen dizinin normal dağılım yasasına sahip olacağını garanti etmediği anlamına gelir.


1. Box-Cox Dönüşümü

N uzunluğundaki orijinal X dizisi için

Tek parametreli Box-Cox dönüşümü aşağıdaki gibi bulunur:


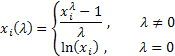
Burada .

Gördüğünüz gibi, bu dönüşümün yalnızca bir parametresi var - lambda. Lambda değeri sıfıra eşitse ilk dizinin logaritmik dönüşümü yapılır, lambda değerinin sıfırdan farklı olması durumunda dönüşüm kuvvet yasasıdır. Lambda parametresi bire eşitse, ilk dizi dağılım yasası değişmeden kalır, ancak dizi kayar; zira birlik değerlerinin her birinden çıkarılır.

Lambda değerine bağlı olarak Box-Cox dönüşümü aşağıdaki özel durumları içerir:


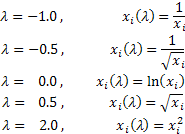
Box-Cox dönüşümünün kullanılması, tüm giriş dizisi değerlerinin pozitif ve sıfırdan farklı olmasını gerektirir. Giriş dizisi bu gereklilikleri karşılamıyorsa, tüm değerlerinin "pozitifliğini" garanti eden hacim tarafından pozitif alana taşınabilir.

Şimdilik yalnızca tek parametreli Box-Cox dönüşümünü inceleyelim; buna uygun bir şekilde giriş verileri hazırlayalım. Giriş verilerinde negatif veya sıfır değerlerden kaçınmak için, her zaman giriş dizisinin en düşük değerini bulacağız ve ek olarak 1e-5'e eşit küçük bir kaydırma yaparak dizinin her bir öğesinden çıkaracağız. Böyle bir ek kaydırma, en düşük değerinin sıfıra eşit olması durumunda, pozitif alana garantili bir dizi yer değiştirmesi sağlamak için gereklidir.

Aslında, bu yer değiştirmeyi "pozitif" dizilere uygulamak gerekli değildir. Ancak yine de dönüşüm sırasında bir güce yükseltirken aşırı büyük değerler alma olasılığını azaltmak için aynı algoritmayı kullanacağız. Böylece, herhangi bir giriş dizisi, kaydırmadan sonra pozitif alanda yer alacak ve sıfıra yakın en düşük değere sahip olacaktır.

Şek. 1'de, lambda parametresinin farklı değerlerine sahip Box-Cox dönüşüm eğrileri gösterilmiştir. Şek. 1 "Box-Cox Dönüşümleri" [3] makalesinden alınmıştır. Grafikteki yatay ızgara, logaritmik ölçekte verilmiştir.

Şek. 1. Çeşitli lambda parametresi değerleri durumunda Box-Cox dönüşümü

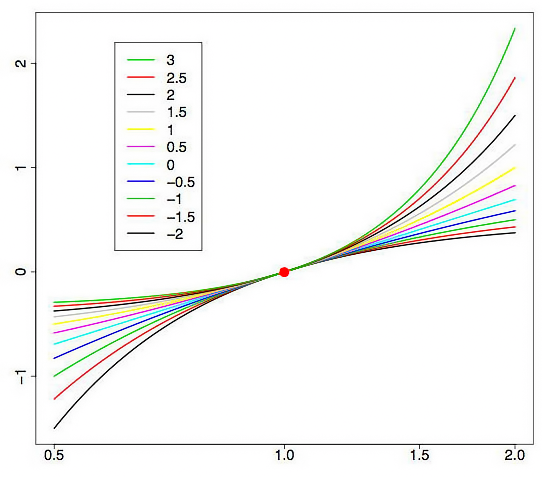
Şek. 1. Çeşitli lambda parametresi değerleri durumunda Box-Cox dönüşümü

Gördüğümüz gibi, ilk dağılımın "kuyrukları" "uzatılmış" veya "bırakılmış" olabilir. Şek. 1'deki üst eğri lambda=3'e karşılık gelirken alt eğri - lambda=-2'ye karşılık gelir.

Ortaya çıkan dizi dağılım yasasının mümkün olduğunca normal yasaya yakın olması için lambda parametresinin optimum değeri seçilmelidir.

Bu parametrenin optimum değerini belirlemenin bir yolu, olabilirlik işlevi logaritmasını maksimize etmektir:

Burada:

Bu, bu işlevin maksimum değerine ulaştığı lambda parametresini seçmemiz gerektiği anlamına gelir.

"Box-Cox Dönüşümleri" [3] makalesinde, normal dağılım işlevinin nicelikleri ile sıralanmış dönüştürülmüş dizi arasındaki korelasyon katsayısının en yüksek değerinin aranmasına dayalı olarak optimum değeri belirlemenin başka bir yolu kısaca ele alınmaktadır. Büyük olasılıkla, başka lambda parametresi optimizasyon yöntemleri bulmak da mümkündür, ancak ilk olarak daha önce bahsedilen maksimum olabilirlik işlevi logaritmasını aramayı tartışalım.

Bunu bulmanın farklı yolları vardır. Örneğin, basit bir arama kullanabiliriz. Bunu yapmak için, düşük bir perdede lambda parametre değerini değiştirerek, seçilen bir aralık içinde olabilirlik işlevi değerini hesaplamalıyız. Ayrıca, olabilirlik işlevinin en yüksek değere sahip olduğu optimum lambda parametresini seçmeliyiz.

Perde mesafesi, lambda parametresinin optimum değer hesaplamasının doğruluğunu belirleyecektir. Perde ne kadar düşükse, doğruluk o kadar yüksek olur, ancak bu durumda gerekli hesaplama miktarı orantılı olarak artar. Hesaplama verimliliğini artırmak için maksimum/minimum işlevini aramaya yönelik çeşitli algoritmalar, genetik algoritmalar ve diğer bazı yöntemler kullanılabilir.


2. Normal Dağılım Yasasına Dönüşüm

Box-Cox dönüşümünün en önemli görevlerinden biri, giriş dizisi dağılım yasasının "normal" şekle indirgenmesidir. Bu dönüşüm yardımıyla böyle bir sorunun ne kadar iyi çözülebileceğini bulmaya çalışalım.

Herhangi bir dikkat dağıtıcı durumdan ve gereksiz tekrardan kaçınmak için, Powell yöntemiyle minimum işlevi arama algoritmasını kullanacağız. Bu algoritma, "Üstel Yumuşatma Kullanarak Zaman Serisi Tahmini" ve "Üstel Yumuşatma Kullanarak Zaman Serisi Tahmini (devamı)" makalelerinde açıklanmıştır.

Dönüşüm parametresinin optimum değerini aramak için CBoxCox sınıfını oluşturmalıyız. Bu sınıfta yukarıda bahsedilen olabilirlik işlevi objektif olarak gerçekleştirilecektir. PowellsMethod sınıfı [4], [5], arama algoritmasını doğrudan gerçekleştiren temel bir sınıf olarak kullanılır.

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CBoxCox class                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Input data
   double            BCDat[];        // Box-Cox data
   int               Dlen;          // Data size
   double            Par[1];         // Parameters
   double            LnX;            // ln(x) sum
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- Lambda initial value
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- input data
      a=dat[i]; Dat[i]=a;
     //--- ln(x) sum
     LnX+=MathLog(a);        
     }
    //--- Powell optimization
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;  
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                            
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=MathLog(Dat[i]);
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

Şimdi, lambda parametresinin optimum değerini bulmak için tek yapmamız gereken, giriş verilerini içeren diziye bağlantı sağlayarak bahsedilen sınıfın CalcPar yöntemine başvurmak. GetPar yöntemine başvurarak elde edilen parametre optimum değerini elde edebiliriz. Daha önce de söylendiği gibi, giriş verileri pozitif olmalıdır.

PowellsMethod sınıfı, çok sayıda değişkenin işlevinin minimumunu arama algoritmasını uygular, ancak bizim durumumuzda yalnızca tek bir parametre optimize edilmiştir. Bu, Par[] dizi boyutunun bire eşit olduğu gerçeğine yol açar. Bu, dizinin yalnızca bir değer içerdiği anlamına gelir. Teorik olarak, bu durumda parametre dizisi yerine standart bir değişken kullanabiliriz, ancak bu, PowellsMethod temel sınıf kodunda değişikliklerin uygulanmasını gerektirecektir. Kaynak MQL5 kodunu yalnızca bir öğe içeren dizileri kullanarak derlersek, muhtemelen herhangi bir sorun olmayacaktır.

CBoxCox::func() işlevinin, lambda parametresinin izin verilebilir değerlerine ait aralığın bir sınırlamasını içerdiği gerçeğini dikkate almalıyız. Bizim durumumuzda bu aralık -5 ile 5 arasındaki değerlerle sınırlıdır. Bu, giriş verilerini lambda derecesine yükseltirken aşırı büyük veya çok küçük değerler elde etmekten kaçınmak için yapılır.

Ayrıca, optimizasyon sırasında aşırı büyük veya çok küçük lambda değerleri elde edersek, bu, dizinin seçilen dönüşüm türü için faydasız olduğunu gösterebilir. Bu nedenle, lambda değerini hesaplarken her durumda makul bir aralığı aşmamak akıllıca olacaktır.


3. Rastgele Diziler

CBoxCox sınıfını kullanarak oluşturduğumuz sözde rastgele dizinin Box-Cox dönüşümünü gerçekleştirecek bir test script dosyası yazalım.

Aşağıda böyle bir script dosyasının kaynak kodu bulunmaktadır.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input array preparation
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- optimization by lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

Gösterilen script dosyasında giriş olarak dönüştürülmüş veri olarak, üstel dağılım yasasına sahip bir sözde rastgele dizi kullanılır. Dizi uzunluğu n değişkeninde ayarlanır ve bu durumda 1600 değere eşittir.

RNDXor128 sınıfı (George Marsaglia, Xorshift RNG) bir sözde rastgele dizi oluşturmak için kullanılır. Bu sınıf, "Zaman Serilerinin Ana Özelliklerinin Analizi" [6] makalesinde açıklanmıştır. BoxCoxTest1.mq5 script dosyası derlemesi için gerekli tüm dosyalar Box-Cox-Tranformation_MQL5.zip arşivindedir. Başarılı bir derleme için bu dosyalar bir dizinde bulunmalıdır.

Gösterilen script dosyası yürütüldüğünde, giriş dizisi oluşturulur, pozitif değerler alanına taşınır ve lambda parametresinin optimum değeri aranır. Ardından, elde edilen lambda değerini ve arama algoritmasının geçiş sayısını içeren mesaj görüntülenir. Sonuç olarak, bcdat[] çıkış dizisinde dönüştürülmüş dizi oluşturulacaktır.

Mevcut haliyle bu script dosyası, yalnızca dönüştürülmüş diziyi daha sonraki kullanım için hazırlamaya olanak tanır ve herhangi bir değişiklik uygulamaz. Bu makale yazılırken, dönüşüm sonuçlarının değerlendirilmesi için "Zaman Serilerinin Ana Özelliklerinin Analizi" [6] makalesinde açıklanan analiz türü seçilmiştir. Bunun için kullanılan script dosyaları, yayınlanan kodların hacmini azaltmak için bu makalede gösterilmemiştir. Aşağıda yalnızca hazır analiz grafik sonuçları sunulmuştur.

Şek. 2'de, BoxCoxTest1.mq5 script dosyasında kullanılan üstel dağılım yasasına sahip sözde rastgele dizi için normal dağılım ölçeği tarafından sağlanan histogram ve grafik gösterilmiştir. Jarque-Bera test sonucu JB=3241,73, p= 0,000. Gördüğümüz gibi, giriş dizisi hiç "normal" değildir ve beklendiği gibi dağılımı üstel olana benzerdir.

Şek. 2

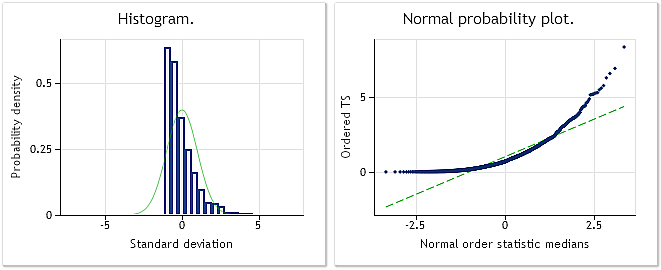
Şek. 2. Üstel dağılım yasasına sahip sözde rastgele dizi. Jarque-Bera testi JB=3241,73, р=0,000.

 Şek. 3

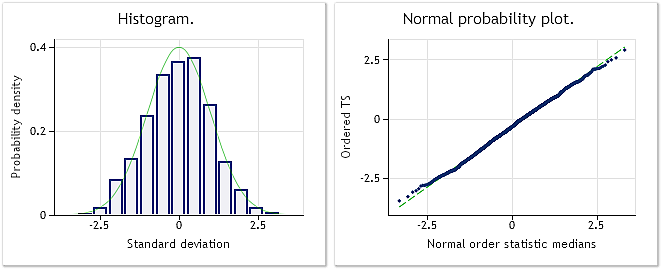
Şek. 3. Dönüştürülmüş dizi. Lambda parametresi=0,2779, Jarque-Bera testi JB=4,73, р=0,094

Şek. 3'te, dönüştürülmüş dizi analizinin sonucu gösterilmiştir. (BoxCoxTest1.mq5 script dosyası, bcdat[] dizisi). Dönüştürülmüş dizi dağılım yasası normale çok daha yakındır ve bu durum Jarque-Bera testi sonuçları JB=4,73, p=0,094 ile de doğrulanmaktadır. Elde edilen lambda parametre değeri=0,2779.

Box-Cox dönüşümü bu örnekte yeterince uygun olduğunu kanıtlamıştır. Görünüşe göre ortaya çıkan dizi "normal" olana çok daha yakın hale gelmiş ve Jarque-Bera testi sonucu JB=3241,73'ten JB=4,73'e düşmüştür. Bu şaşırtıcı değildir; zira seçilen dizi bu tür bir dönüşüme oldukça iyi uymaktadır.

Sözde rastgele dizinin Box-Cox dönüşümünün başka bir örneğini inceleyelim. Box-Cox dönüşümü için kuvvet yasası yapısını göz önünde bulundurarak "uygun" bir giriş dizisi oluşturmalıyız. Bunu gerçekleştirmek için, (halihazırda normal olana yakın dağılım yasasına sahip olan) bir sözde rastgele dizi oluşturmamız ve ardından tüm değerlerini 0,35'in kuvvetine yükselterek onu çarpıtmamız gerekir. Box-Cox dönüşümünün giriş dizisine orijinal normal dağılımı büyük bir kesinlikle döndürmesini bekleyebiliriz.

Aşağıda, BoxCoxTest2.mq5 metin script dosyasının kaynak kodu verilmiştir.

Bu script dosyası öncekinden yalnızca, içinde başka bir giriş dizisinin oluşturulmuş olmasıyla farklılık gösterir.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input data array
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- optimization by lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- input data
//-- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

Normal dağılım yasasına sahip giriş sözde rastgele dizisi, gösterilen script dosyasında oluşturulur. Bu, pozitif değerler alanına kaydırılır ve ardından bu dizinin tüm öğeleri 0,35'in kuvvetine yükseltilir. Script dosyası işlemi tamamlandıktan sonra dat[] dizisi giriş dizisini içerirken, bcdat[] dizisi dönüştürülmüş olanı içerir.

Şekil 4'te, 0,35 kuvvetine yükseltilmesi nedeniyle orijinal normal dağılımını kaybetmiş giriş dizisinin özellikleri gösterilmiştir. Bu durumda, Jarque-Bera testi JB=3609,29, p= 0,000'ı gösterir.

Şek. 4

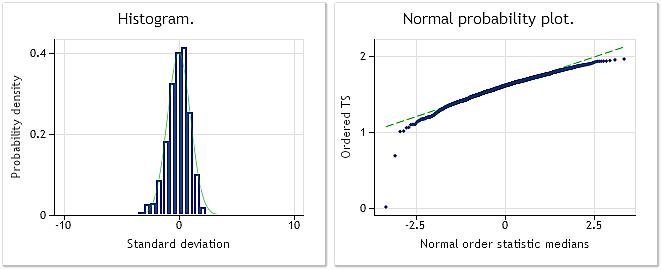
Şek. 4. Giriş sözde rastgele dizisi. Jarque-Bera testi JB=3609,29, p=0,000.

Şek. 5

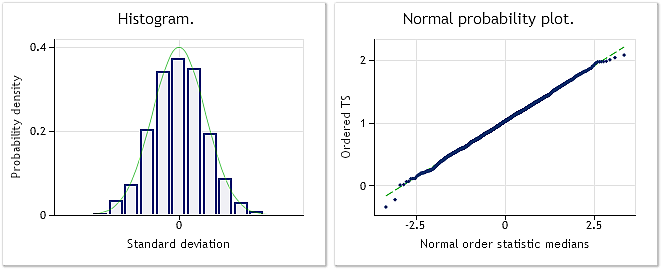
Şek. 5. Dönüştürülmüş dizi. Lambda parametresi=2,9067, Jarque-Bera testi JB=0,30, p=0,859

Şekil 5'te gösterildiği gibi, dönüştürülmüş dizi, normal olana yeterince yakın dağılım yasasına sahiptir; bu da Jarque-Bera testi değeri JB=0,30, p=0,859 ile doğrulanır.

Box-Cox dönüşümü kullanımına ilişkin bu örnekler çok iyi sonuçlar vermiştir. Ancak her iki durumda da bu dönüşüm için en uygun olan dizileri ele aldığımızı unutmamalıyız. Bu nedenle, bu sonuçlar sadece oluşturduğumuz algoritmanın performansının bir doğrulaması olarak görülebilir.


4. Fiyat Teklifleri

Box-Cox dönüşümünü uygulayan algoritmanın normal performansını onayladıktan sonra, normal dağılım yasasına indirgemek istediğimiz için onu gerçek Forex fiyat tekliflerine uygulamayı denemeliyiz.

Test fiyat teklifleri olarak "Üstel Yumuşatma Kullanarak Zaman Serileri Tahmini (devamı)" makalesinde açıklanan dizileri kullanacağız [5]. Bunlar, Box-Cox-Tranformation_MQL5.zip arşivinin \Dataset2 dizinine yerleştirilirler ve 1200 değeri uygun dosyalara kaydedilmiş gerçek fiyat teklifleri sağlarlar. Bu dosyalara erişim sağlamak için, ayıklanan \Dataset2 klasörü terminalin \MQL5\Files dizinine yerleştirilmelidir.

Bu fiyat tekliflerinin durağan diziler olmadığını varsayalım. Dolayısıyla, analiz sonuçlarını sözde genel popülasyona genişletmeyeceğiz, ancak onları yalnızca bu belirli sonlu uzunluk dizisinin özellikleri olarak ele alacağız.

Ayrıca, durağanlık yoksa, aynı para birimi çiftinin farklı fiyat teklifi parçalarının çok farklı dağılım yasalarını takip ettiği tekrar belirtilmelidir.

Bir dosyadan dizi değerlerini okumaya ve Box-Cox dönüşümünü gerçekleştirmeye izin veren bir script dosyası oluşturalım. Bu, yukarıda gösterilen test script dosyalarından yalnızca giriş dizisi oluşturma açısından farklılık gösterecektir. BoxCoxTest3.mq5 script dosyası ekteki arşive yerleştirilirken, böyle bir script dosyasının kaynak kodu aşağıda verilmiştir.

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- input data file
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- data reading
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- input data array
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- lambda parameter optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

Tüm değerler (bizim durumumuzda bunlardan 1200 tane vardır), bu script dosyasındaki dat[] dizisine, adı fname değişkeninde ayarlanan fiyat teklifleri dosyasından alınır. Daha sonra, ilk dizinin kaydırılması, optimum parametre değerinin aranması ve Box-Cox dönüşümü yukarıda açıklandığı gibi gerçekleştirilir. Script dosyası yürütüldükten sonra, dönüşüm sonucu bcdat[] dizisinde bulunur.

Gösterilen kaynak kodundan da anlaşılacağı gibi, dönüşüm için script dosyasında EURUSD M1 fiyat teklifi dizisi seçilmiştir. Orijinal ve dönüştürülmüş dizi analizi sonucu Şek. 6 ve 7'de gösterilmiştir.

Şek. 6

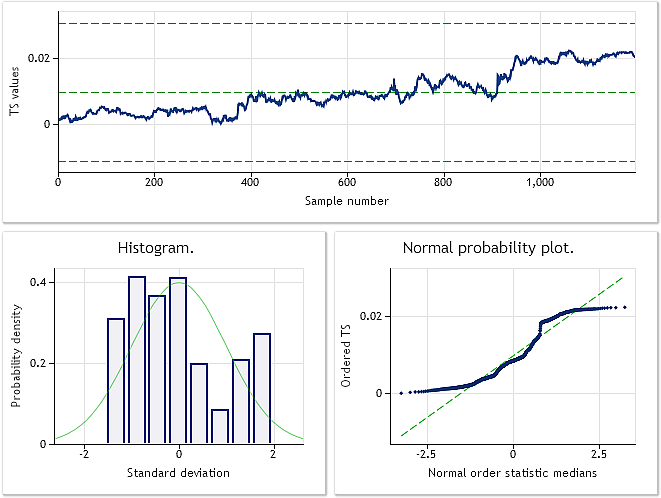
Şek. 6. EURUSD M1 giriş dizisi. Jarque-Bera testi JB=100,94, p=0,000.

Şek. 7

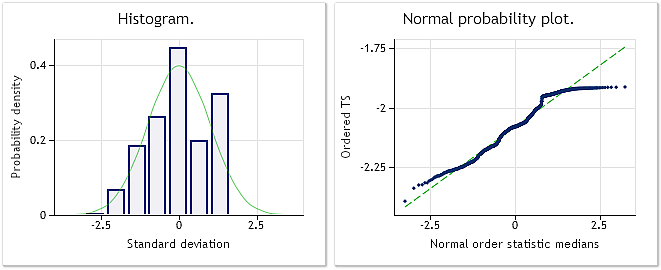
Şek. 7. Dönüştürülmüş dizi. Lambda parametresi=0,4146, Jarque-Bera testi JB=39,30, p=0,000

Şek. 7'de gösterilen özelliklere göre, EURUSD M1 fiyat teklifleri dönüşümünün sonucu, daha önce gösterilen sözde rastgele dizi dönüşüm sonuçları kadar etkileyici değildir. Box-Cox dönüşümü, yeterince evrensel olduğu düşünülse de, her tür giriş dizisinin üstesinden gelemez. Örneğin, kuvvet yasası dönüşümünün iki tepeli dağılımı normale dönüştürmesini beklemek pratik değildir.

Şek. 7'de gösterilen dağılım yasası pek normal kabul edilemese de, önceki örneklerde olduğu gibi yine de Jarque-Bera testi değerlerinde önemli bir düşüş görebiliriz. Orijinal dizi için JB=100,94 iken, dönüşümden sonra JB=39,30'u gösterir. Bu, dağılım yasasının dönüşümden sonra bir nebze normal değerlere yaklaşmayı başardığı anlamına gelir.

Diğer fiyat tekliflerinin farklı parçaları dönüştürülürken yaklaşık olarak aynı sonuçlar elde edilmiştir. Box-Cox dönüşümü her seferinde dağılım yasasını normal olana az ya da çok yaklaştırmıştır. Ancak, hiçbir zaman normal olmamıştır.

Çeşitli fiyat teklifi dönüşümleri ile yapılan bir dizi deneme, tam olarak beklenen bir sonuca varılmasını sağlar – Box-Cox dönüşümü, Forex fiyat teklifleri dağılım yasasını normal olana yaklaştırmaya izin verir, ancak dönüştürülmüş veri dağılım yasasının gerçek normalliğine ulaşılmasını garanti edemez.

Hala orijinal diziyi normal diziye getirmeyen dönüşümü gerçekleştirmek mantıklı mı? Bu sorunun kesin bir cevabı yoktur. Her özel durumda, Box-Cox dönüşümüne duyulan ihtiyaçla ilgili bireysel bir karar almalıyız. Bu durumda, bir çok şey, fiyat teklifi analizinde kullanılan parametrik yöntemlerin türüne ve bu yöntemlerin ilk verilerin normal dağılım yasasından sapmasına karşı duyarlılığına bağlı olacaktır.


5. Trend Kaldırma

Şek. 6'nın üst kısmında, BCTransform.mq5 script dosyasında kullanılan EURUSD M1 orijinal dizisinin grafiği gösterilmiştir. Tüm dizi boyunca değerlerinin neredeyse eşit bir şekilde arttığı kolayca görülebilir. İlk tahminde, dizinin doğrusal trendi içerdiği sonucuna varabiliriz. Böyle bir "trendliliğin" varlığı, çeşitli dönüşümler gerçekleştirmeden ve alınan diziyi analiz etmeden önce trendi hariç tutmaya çalışmamız gerektiğini gösterir.

Analiz edilen giriş dizilerinden bir trendin kaldırılması muhtemelen kesinlikle tüm durumlar için uygun bir yöntem olarak düşünülmemelidir. Ama diyelim ki, Şek. 6'da gösterilen diziyi, içindeki periyodik (veya döngüsel) bileşenleri bulmak için analiz edeceğiz. Bu durumda, trendin parametrelerini tanımladıktan sonra kesinlikle doğrusal trendi giriş dizisinden çıkarabiliriz.

Doğrusal bir trendin kaldırılması, periyodik bileşenlerin saptanmasını etkilemeyecektir. Hatta bu, yararlı olabilir ve seçilen analiz yöntemine bağlı olarak bu tür analizlerin sonuçlarını bir dereceye kadar daha doğru veya güvenilir hale getirebilir.

Bazı durumlarda bir trendin kaldırılmasının faydalı olabileceğine karar verdiysek, o zaman Box-Cox dönüşümünün bir trend hariç tutulduktan sonra bir dizinin üstesinden nasıl geldiğini incelemek muhtemelen mantıklıdır.

Her durumda, bir trendi kaldırırken, trend tahmini için hangi eğrinin kullanılması gerektiğine karar vermemiz gerekecek? Bu, düz bir çizgi, daha yüksek dereceli eğriler, hareketli ortalamalar vb. olabilir. Bu durumda optimum eğri seçimi konusuna takılmamak için deyim yerindeyse uç sürümünü seçelim. Orijinal dizideki artışları, yani orijinal dizinin kendisi yerine mevcut ve önceki değerleri arasındaki farkları kullanacağız.

Artış analizini tartıştığımız anda, ilgili bazı noktalar hakkında yorum yapmamak mümkün değil.

Çeşitli makalelerde ve forumlarda, artış analizine geçişin gerekliliği, böyle bir geçişin özellikleri hakkında yanlış izlenim bırakabilecek şekilde gerekçelendirilir. Artış analizine geçiş, genellikle orijinal bir diziyi durağan olana dönüştürebilen veya dağılım yasasını normalleştirebilen bir tür dönüşüm olarak tanımlanır. Peki bu doğru mu? Bu soruyu cevaplamaya çalışalım.

Artış analizine geçişin özünün, orijinal bir dizinin iki bileşene bölünmesi gibi çok basit bir fikirden oluştuğu gerçeğinden başlamalıyız. Bunu, aşağıdaki gibi gösterebiliriz.

Giriş dizisine sahip olduğumuzu varsayalım

Ve her ne sebeple olursa olsun, onu bir trend ve orijinal dizi öğelerinden trend değerlerinin çıkarılmasından sonra ortaya çıkan bazı kalan öğeler olarak bölmeye karar verdik. Bir trend tahmini için iki dizi öğesine eşit bir yumuşatma dönemine sahip basit bir hareketli ortalama kullanmaya karar verdiğimizi varsayalım.

Böyle bir hareketli ortalama, iki bitişik dizi öğesinin toplamının ikiye bölünmesiyle hesaplanabilir. Bu durumda, orijinal diziden ortalamanın çıkarılmasından elde edilen kalan kısım, aynı bitişik öğeler arasındaki farkın ikiye bölünmesine eşit olacaktır.

Yukarıda belirtilen ortalama değeri S olarak gösterelim, kalan kısım D olacak. Daha fazla netlik için kalıcı faktör 2'yi denklemin sol kısmına taşırsak, şunu elde ederiz:


Oldukça basit dönüşümlerimizi tamamladıktan sonra, orijinal dizimizi, biri bitişik dizilerin değerlerinin toplamı ve diğeri farklardan oluşan iki bileşene böldük. Toplamlar trendi oluştururken, bunlar tam olarak artışlar olarak adlandırdığımız dizilerdir.

Bu bağlamda, artışları orijinal dizinin bir parçası olarak değerlendirmek daha mantıklı olacaktır. Dolayısıyla, artış analizine geçersek, toplamlarla tanımlanan dizinin diğer kısmının, elbette ayrı olarak analiz etmediğimiz sürece, genellikle basitçe göz ardı edildiğini unutmamalıyız.

Dizinin bu bölünmesiyle ne tür faydalar elde edebileceğimize ilişkin bir fikir edinmenin en kolay yolu, spektral yöntemi uygulamaktır.

Doğrudan yukarıda verilen ifadelerden, S bileşeninin, h=1,1 darbe özelliğine sahip düşük frekanslı filtrenin kullanımıyla orijinal dizi filtrelemesinin bir sonucu olduğunu elde edebiliriz. Buna göre, D bileşeni, h=-1,1 darbe özelliğine sahip yüksek frekanslı filtrenin kullanımıyla yapılan filtrelemenin bir sonucudur. Şek. 8'de, bu tür filtrelerin frekans özellikleri nominal olarak gösterilmiştir.

Şek. 8

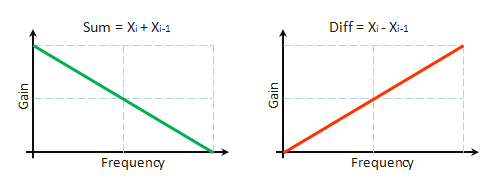
Şek. 8. Genlik-frekans özellikleri

Diyelim ki dizinin kendisinin doğrudan analizinden farklılıklarının analizine geçtik. Burada ne bekleyebiliriz? Bu durumda çeşitli seçenekler var. Biz yalnızca bazılarına kısaca göz atacağız.

  1. Analiz edilen sürecin temel enerjisinin orijinal dizinin düşük frekans bölgesinde yoğunlaşması durumunda, fark analizine geçiş yalnızca bu enerjiyi bastırarak analize devam etmeyi daha karmaşık ve hatta imkansız hale getirecektir;
  2. Analiz edilen sürecin temel enerjisinin orijinal dizinin yüksek frekans bölgesinde yoğunlaşması durumunda, fark analizine geçiş, girişim yapan düşük frekanslı bileşenlerin filtrelenmesi nedeniyle olumlu etkilere yol açabilir. Ancak bu, yalnızca böyle bir filtrelemenin analiz edilen sürecin özelliklerini önemli ölçüde etkilememesi halinde mümkündür;
  3. Analiz edilen sürecin enerjisinin dizi frekans aralığının tamamına eşit olarak dağıldığı durumdan da bahsedebiliriz. Bu durumda, düşük frekanslı kısmını bastırarak farklılıklarının analizine geçişten sonra süreci geri döndürülemez bir şekilde çarpıtacağız.

Benzer şekilde, diğer trend kombinasyonları, kısa vadeli trend, parazit yapan gürültü vb. için farklılık analizine geçişin sonuçları hakkında sonuçlar çıkarabiliriz. Ancak her durumda, fark analizine geçiş, analiz edilen sürecin durağan bir formuna yol açmayacak ve dağılım sürecini normalleştirmeyecektir.

Yukarıda belirtilenlere dayanarak, farklılıklar analizine geçişten sonra bir dizinin otomatik olarak "iyileşmediği" sonucuna varabiliriz. Bazı durumlarda, giriş dizisi hakkında daha net bilgi edinmek için hem giriş dizisini hem de bitişik değerlerinin toplamları ile birlikte farklılıkları analiz etmenin daha iyi olduğunu varsayabiliriz, ancak elde edilen tüm sonuçların ortak değerlendirmesine dayalı olarak bu dizinin özellikleri hakkında nihai sonuçlar çıkarılmalıdır.

Şimdi makalemizin konusuna dönelim ve Şek.6'da gösterilen EURUSD M1 dizisinin artış analizine geçiş durumunda Box-Cox dönüşümünün nasıl davrandığını görelim. Bunu yapmak için, daha önce gösterilen BoxCoxTest3.mq5 script dosyasını kullanacağız; burada dosyadaki bu dizi değerlerini hesapladıktan sonra dizi değerlerini farklılıklar (artışlar) ile değiştireceğiz. Script dosyası kaynak kodunda başka hiçbir değişiklik yapılmadığı için, yayınlamanın bir anlamı yoktur. Bunun yerine yalnızca işlevsellik analizinin sonuçlarını göstereceğiz.

EURUSD M1 artışları. Jarque-Bera testi JB=32494,8, p=0,000

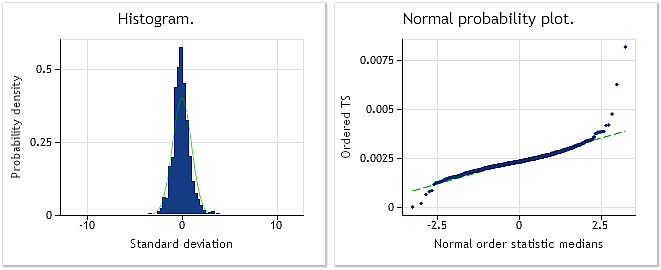
Şek. 9. EURUSD M1 artışları. Jarque-Bera testi JB=32494,8, p=0,000

Şek. 10. Dönüştürülmüş dizi. Lambda parametresi=0,6662, Jarque-Bera testi JB=10302,5, p=0,000

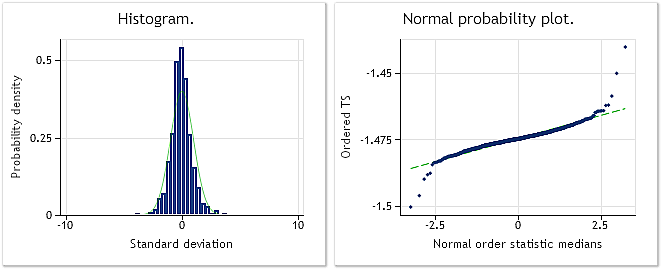
Şek. 10. Dönüştürülmüş dizi. Lambda parametresi=0,6662, Jarque-Bera testi JB=10302,5, p=0,000

Şek. 9'da, EURUSD M1 artışlarından (farklılıklardan) oluşan dizinin özellikleri gösterilirken, Şek. 10'da Box-Cox dönüşümünden sonra elde edilen özellikleri gösterilmiştir. Jarque-Bera testi değerinin dönüşümden sonra JB = 32494,8'den JB = 10302,5'e üç kattan fazla azalmış olmasına rağmen, dönüştürülmüş dizi dağılım yasası hala normal olmaktan uzaktır.

Ancak Box-Cox dönüşümünün artışlar dönüşümünün tam olarak üstesinden gelemeyeceğini düşünerek aceleci sonuçlara varmamalıyız. Yalnızca özel bir durumu ele aldık. Diğer giriş dizileriyle ilgilenirken, tamamen farklı sonuçlar elde edebiliriz.


6. Atıfta Bulunulan Örnekler

Box-Cox dönüşümünün daha önce atıfta bulunulan tüm örnekleri, orijinal dizi dağılım yasasının normal olana veya belki de mümkün olduğunca normal olana yakın olan yasaya indirgenmesi gerektiği durumla ilgilidir. Başta da belirtildiği gibi, incelenen bir dizi dağılım yasasının normalden sapmasına oldukça duyarlı olabilen parametrik analiz yöntemleri kullanılırken böyle bir dönüşüm gerekli olabilir.

Gösterilen örnekler, dönüşümden sonra tüm durumlarda, Jarque-Bera testi sonuçlarına göre, orijinal dizilere kıyasla normale daha yakın olan dağılım yasasına sahip dizileri aldığımızı göstermiştir. Bu gerçek, Box-Cox dönüşümünün çok yönlülüğünü ve verimliliğini açıkça göstermektedir.

Ancak Box-Cox dönüşümünün olasılıklarını abartmamalı ve herhangi bir giriş dizisinin kesinlikle normal bir diziye dönüştürüleceğini varsaymamalıyız. Yukarıdaki örneklerden de anlaşılacağı gibi, bu, doğru olmaktan uzaktır. Gerçek fiyat teklifleri için ne orijinal ne de dönüştürülmüş dizi normal kabul edilemez.

Box-Cox dönüşümü şimdiye kadar yalnızca daha görsel, tek parametreli biçiminde ele alındı. Bu, onunla ilk karşılaşmayı basitleştirmek için yapıldı. Bu yaklaşım, bu dönüşümün becerilerini göstermek için haklı gösterilebilir, ancak pratik amaçlar için sunumunun daha genel bir biçimini kullanmak muhtemelen daha iyi olacaktır.


7. Box-Cox Dönüşümünün Genel Şekli

Box-Cox dönüşümünün yalnızca pozitif ve sıfır olmayan değerlere sahip diziler için geçerli olduğu unutulmamalıdır. Pratikte bu gereklilik, bir dizinin pozitif alana basit bir kaymasıyla kolayca karşılanır, ancak pozitif alandaki kaymanın büyüklüğü, dönüşüm sonucu üzerinde doğrudan bir etkiye sahip olabilir.

Bu nedenle, kaydırma değeri ek bir dönüşüm parametresi olarak kabul edilebilir ve dizi değerlerinin negatif alana girmesine izin vermeden lambda parametresi ile birlikte optimize edilebilir.

N uzunluğundaki orijinal X dizisi için:

İki parametreli Box-Cox dönüşümünün daha genel biçimini belirleyen ifadeler şunlardır:

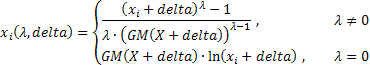
Burada:

;

GM() - geometrik ortalama.

Dizinin geometrik ortalaması şu şekilde hesaplanabilir:

Gördüğümüz gibi, gösterilen ifadelerde zaten iki parametre kullanılıyor - lambda ve delta. Şimdi, dönüşüm sırasında bu parametrelerin her ikisini de aynı anda optimize etmemiz gerekiyor. Algoritmanın hafif karmaşıklığına rağmen, ek bir parametrenin eklenmesi dönüşüm verimliliğini kesinlikle artırabilir. Ayrıca, daha önce kullanılan dönüşümle karşılaştırıldığında ifadelerde ek normalleştirme faktörleri ortaya çıktı. Bu faktörlerle dönüşüm sonucu lambda parametresi değişikliği sırasında boyutunu koruyacaktır.

Box-Cox dönüşümü hakkında daha fazla bilgi [7], [8] adresinde bulunabilir. Aynı türdeki diğer bazı dönüşümler kısaca [8]'de açıklanmıştır.

Mevcut, daha genel dönüşüm formunun ana özellikleri şu şekildedir:

  1. Dönüşümün kendisi, giriş dizisinden yalnızca pozitif değerler içermesini gerektirir. Ek delta parametresinin dahil edilmesi, bazı belirli koşullar yerine getirilirken dizinin gerekli kaydırmasının otomatik olarak gerçekleştirilmesine izin verir;
  2. Delta parametresi optimum değerini seçerken, büyüklüğü tüm dizi değerlerinin "pozitifliğini" garanti etmelidir;
  3. Sıfır değerine yakın değişiklikleri içeren lambda parametresinin değiştirilmesi durumunda dönüşüm süreklidir;
  4. Dönüşüm sonucu, lambda parametre değerinin değiştirilmesi durumunda boyutunu korur.

Olabilirlik işlevi logaritma kriteri, lambda parametresi optimum değeri aranırken, daha önce atıfta bulunulan tüm örneklerde kullanıldı. Elbette, dönüşüm parametrelerinin optimum değerini tahmin etmenin tek yolu bu değildir.

Örnek olarak, artan şekilde sıralanan dönüştürülmüş bir dizi ile normal dağılım işlevi niceliklerinin bir dizisi arasındaki korelasyon katsayısının maksimum değerinin arandığı parametre optimizasyonu yönteminden söz edebiliriz. Bu varyanta daha önce makalede değinilmiştir. Normal dağılım işlevi niceliklerinin değerleri James J. Filliben [9] tarafından önerilen ifadelere göre hesaplanabilir.

İki parametreli dönüşümün genel biçimini belirleyen ifadeler, daha önce düşünülenlerden kesinlikle daha kullanışsızdır. Belki de bu tür dönüşümlerin matematiksel ve istatistiksel paket programlarda oldukça nadir kullanılmasının nedeni budur. Box-Cox dönüşümünü gerektiğinde daha genel bir biçimde kullanma imkanına sahip olmak için atıfta bulunulan ifadeler MQL5'te uygulanmıştır.

CFullBoxCox.mqh dosyası, dönüşüm parametrelerinin optimum değerini arama işlemini gerçekleştiren CFullBoxCox sınıfının kaynak kodunu içerir. Daha önce de belirtildiği gibi, optimizasyon işlemi korelasyon katsayısının hesaplanmasına dayanmaktadır.

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CFullBoxCox class                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // data size
  double Dat[];                    // input data array
  double Shift[];                  // input data array with the shift
  double BCDat[];                  // transformed data (Box-Cox)
  double Mean;                     // transformed data average value
  double Cdf[];                    // Quantile of the distribution cumulative function
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // correlation coefficient 
  double DeltaMin;                 // Delta minimum value
  double DeltaMax;                 // Delta maximum value
  double Par[2];                   // parameters array
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // the function opposite to the normal distribution function
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- copy the input data array
  ArrayCopy(Dat,dat);
  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- calculation of the distribution cumulative function Quantile
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- calculation of the sum of Quantile^2
    Scdf+=Cdf[i]*Cdf[i];
    }

//--- square root of the sum of Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- copy the input data
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- Delta minimum value
  DeltaMin=1e-5-min;
//--- Delta maximum value
  DeltaMax=(max-min)*200-min;
//--- Lambda initial value
  Par[0]=1.0;
//--- Delta initial value
  Par[1]=(max-min)/2-min;
//--- optimization using Powell method
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- geometric mean
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
       //--- average value
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
      //--- average value
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- sorting of the transformed data array
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- correlation coefficient
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| The function opposite to the normal distribution function        |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

Optimizasyon sırasında dönüşüm parametrelerinin değişiklik aralığına bazı sınırlamalar uygulanır. Lambda parametre değeri 5,0 ve -5,0 değerleriyle sınırlıdır. Delta parametreleri için sınırlamalar, giriş dizisinin minimum değerine göre belirlenir. Bu parametre DeltaMin=(0,00001-min) ve DeltaMax=(maks.-min)*200-min değerleriyle sınırlıdır; burada min ve maks., giriş dizisi öğelerinin minimum ve maksimum değerleridir.

FullBoxCoxTest.mq5 script dosyası, CFullBoxCox sınıfının kullanımını gösterir. Bu script dosyasının kaynak kodu aşağıda gösterilmiştir.

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- input file name
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- reading the data
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- shifted input data array
   ArrayResize(shift,n);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- lambda and delta parameters optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- geometric mean
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- input data
//--- shift[] <-- input data with the shift
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

Giriş dizisi, script dosyasının başlangıcındaki dosyadan dat[] dizisine yüklenir ve ardından dönüşüm parametrelerinin optimum değerleri için arama yapılır. Daha sonra, elde edilen parametreler kullanılarak dönüşümün kendisi gerçekleştirilir. Sonuç olarak, dat[] dizisi orijinal diziyi, shift[] dizisi delta değeriyle kaydırılan orijinal diziyi ve bcdat[] dizisi Box-Cox dönüşümünün sonucunu içerir.

FullBoxCoxTest.mq5 script dosyası derlemesi için gerekli tüm dosyalar Box-Cox-Tranformation_MQL5.zip arşivinde bulunur.

Kullandığımız test dizilerinin dönüşümü, FullBoxCoxTest.mq5 script dosyasının yardımıyla gerçekleştirilir. Beklendiği gibi, elde edilen verilerin analizi sırasında bu iki parametreli dönüşüm türünün tek parametreli türe göre biraz daha iyi sonuçlar verdiği sonucuna varabiliriz. Örneğin, analiz sonuçları Şek. 6'da gösterilen EURUSD M1 dizisi için Jarque-Bera testi değeri JB=100,94'ü içermiştir. JB=39,30 tek parametreli dönüşümden sonra (bkz. Şek. 7), ancak iki parametreli dönüşümden sonra (FullBoxCoxTest.mq5 script dosyası) bu değer JB=37,49'a düşmüştür.


Sonuç

Bu makalede, Box-Cox dönüşüm parametrelerinin, ortaya çıkan dizi dağılım yasasının mümkün olduğunca normal olana yakın olması için optimize edildiği durumları inceledik. Ancak pratikte Box-Cox dönüşümünün biraz farklı bir şekilde kullanılması gerektiği durumlar ortaya çıkabilir. Örneğin, zaman dizilerini tahmin ederken aşağıdaki algoritma kullanılabilir:

  1. Box-Cox dönüşüm parametreleri değerlerinin ve tahmin modellerinin ön değerleri seçilir;
  2. Giriş verilerinin Box-Cox dönüşümü gerçekleştirilir;
  3. Tahmin, mevcut parametrelere göre gerçekleştirilir;
  4. Tahmin sonuçları için Ters Box-Cox Dönüşümü yapılır;
  5. Tahmin hatası, dönüştürülmemiş giriş dizisi ile değerlendirilir;
  6. Tahmin hatasını en aza indirmek için parametre değerleri değiştirilir ve algoritma adım 2'ye döner.

Yukarıdaki algoritmada, tahmin hatası minimum kriteri ile tahmin modeli parametrelerinin yanı sıra dönüşüm parametreleri de minimize edilecektir. Bu durumda, Box-Cox dönüşümünün amacı, giriş dizisinin normal dağılım yasasına dönüştürülmesi değildir.

Şimdi, minimum tahmin hatasını sağlayan dağılım yasasını almak için giriş dizisini dönüştürmek gerekiyor. Seçilen tahmin yöntemine bağlı olarak, bu dağılım yasasının mutlaka normal olması gerekmez.

Box-Cox dönüşümü yalnızca pozitif ve sıfır olmayan değerlere sahip diziler için geçerlidir. Giriş dizisinin kaydırılması, diğer tüm durumlarda gerçekleştirilmelidir. Dönüşümün bu özelliğinin kesinlikle dezavantajlarından biri olduğu söylenebilir. Ancak buna rağmen, Box-Cox dönüşümü muhtemelen aynı türden diğer dönüşümler arasında en çok yönlü ve verimli araçtır.


Referans Listesi

  1. А.N. Porunov. Box-Сox Transformation and the Illusion of «Normality» of Macroeconomic Series. "Business Informatics" journal, №2(12)-2010, pp. 3-10.
  2. Mohammad Zakir Hossain, The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses. Journal of Emerging Trends in Economics and Management Sciences (JETEMS) 2(1):32-39.
  3. Box-Cox Transformations.
  4. The article "Time Series Forecasting Using Exponential Smoothing".
  5. The article "Time Series Forecasting Using Exponential Smoothing (continued)".
  6. Analysis of the Main Characteristics of Time Series.
  7. Power transform.
  8. Draper N.R. and H. Smith, Applied Regression Analysis, 3rd ed., 1998, John Wiley & Sons, New York.
  9. Q-Q plot.

MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/363

Ekli dosyalar |
ZIP indir
box-cox-transformation_mql5.zip (91.48 KB)
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.

Bu yazarın diğer makaleleri

Tartışmaya git
Getting Rid of Self-Made DLLs Getting Rid of Self-Made DLLs
MQL5 dil işlevi, görevleri yerine getirmek için yeterli değilse, bir MQL5 programcısı ek araçlar kullanmak zorundadır. Başka bir programlama diline geçmeli ve bir ara DLL oluşturmalıdır. MQL5, çeşitli veri türlerini sunma ve bunları API'a aktarma olanağına sahiptir, ancak ne yazık ki, MQL5, kabul edilen işaretçiden veri ayıklama ile ilgili sorunu çözemez. Bu makalede, tüm "i"leri işaretleyeceğiz ve karmaşık veri türlerini değiştirmenin ve bunlarla çalışmanın basit mekanizmalarını göstereceğiz.
Yeni Müşteriler İçin Birkaç İpucu Yeni Müşteriler İçin Birkaç İpucu
Genellikle çeşitli ünlü kişilere atfedilen meşhur bir söz vardır: "Hata yapmıyorsan, hiçbir şey yapmıyorsun demektir." Aylaklığın kendisinin bir hata olduğunu düşünmedikçe, bu ifadeye itiraz etmesi zor. Ancak gelecekteki hatalarınızın sayısını en aza indirmek için her zaman geçmişteki hatalarınızı (kendinizin ve başkalarının) analiz edebilirsiniz. Aynı ad hizmetinde işler yürütülürken ortaya çıkabilecek olası durumları gözden geçirmeye çalışacağız.
MQL5.community'de Kim Kimdir? MQL5.community'de Kim Kimdir?
MQL5.com web sitesi hepinizi oldukça iyi hatırlar! İleti dizilerinizden kaç tanesinin etkileyici olduğu, makalelerinizin ne kadar popüler olduğu ve Kod Tabanı'nda programlarınızın ne sıklıkla indirildiği... – Bu, MQL5.com'da hatırlananların yalnızca küçük bir kısmı. Başarılarınız profilinizde mevcut, peki ya genel görünüm? Bu makalede tüm MQL5.community üyelerinin başarılarının genel görünümünü göstereceğiz.
Çoklu Regresyon Analizi. Strateji Oluşturucu ve Test Cihazı Bir Arada Çoklu Regresyon Analizi. Strateji Oluşturucu ve Test Cihazı Bir Arada
Makalede, alım satım sistemlerinin geliştirilmesi için çoklu regresyon analizinin kullanım yollarına ilişkin bir açıklama verilmiştir. Ayrıca, strateji arama otomasyonu için regresyon analizinin kullanımı gösterilmiştir. Programlamada yüksek yeterlilik gerektirmeden oluşturulan ve bir EA'ya entegre edilen bir regresyon denklemi örnek olarak verilmiştir.