- Функции потерь
- Метод обратного распространения градиента ошибки
- Методы оптимизации нейронных сетей
Метод обратного распространения градиента ошибки
После того, как мы определились с функцией потерь, можно перейти к обучению нейронной сети. Сам процесс обучения сводится к итерационному подбору параметров нейронной сети (синаптических коэффициентов), при которых значение функции потерь нейронной сети будет минимально.
Из прошлого раздела мы узнали, что функция потерь подбирается выпуклой вниз. Следовательно, начиная обучение из любой точки на графике функции потерь, мы должны двигаться в сторону минимизации ошибки. Для сложных функций, таких как нейронная сеть, наиболее удобным способом является метод градиентного спуска.
Градиентом функции многих переменных (которой является нейронная сеть) называется вектор, состоящий из частных производных функции по ее аргументам. Из курса математики мы знаем, что производная функции характеризует скорость изменения функции в данной точке.
Следовательно, градиент указывает направление наискорейшего роста функции. Двигаясь в направлении антиградиента (обратном к градиенту), мы будем спускаться с максимальной скоростью к минимуму функции.
Наш алгоритм действий будет следующим:
- Инициализируем весовые коэффициенты нейронной сети одним из способов, описанных ранее.
- Вычисляем прогнозные данные на обучающей выборке.
- С помощью функции потерь вычисляем погрешность вычислений нейронной сети.
- Определяем градиент функции потерь в полученной точке.
- Корректируем синаптические коэффициенты нейронной сети в сторону антиградиента.
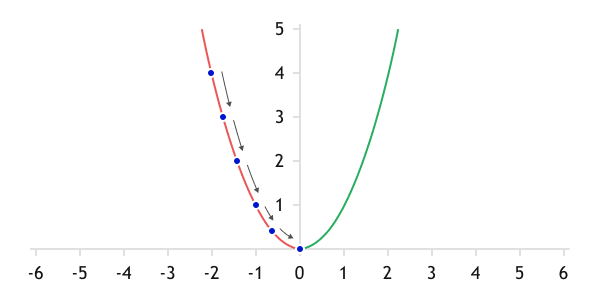
Градиентный спуск
Так как чаще всего будет использоваться нелинейная функция потерь, то и в каждой точке на графике функции потерь направление вектора антиградиента будет меняться. Поэтому, снижаться к минимуму функции потерь мы будем постепенно, с каждой итерацией все ближе и ближе к минимуму.
На первый взгляд, алгоритм довольно прост и логичен. Но как нам технически реализовать пункт 5 нашего алгоритма в случае многослойной нейронной сети?
Данный вопрос решается с применением алгоритма обратного распространения градиента ошибки, который состоит из двух блоков:
- Прямой проход. Пункт 2 из нашего алгоритма выше. Во время прямого прохода на вход нейронной сети подается набор данных из обучающей выборки и производится их обработка в нейронной сети последовательно от входного до выходного слоя. При этом сохраняются промежуточные значения на каждом нейроне.
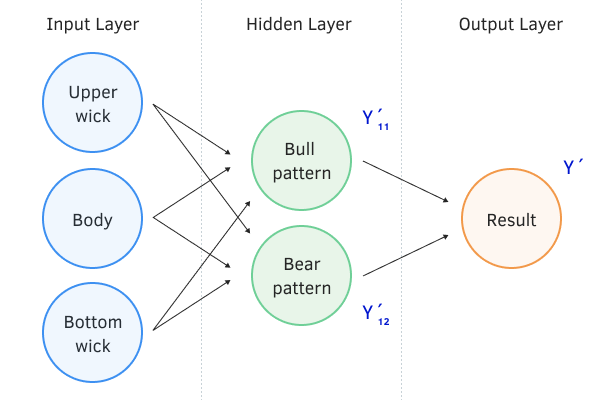
Прямой проход нейронной сети
- Обратный проход включает пункты 3–5 нашего алгоритма.
В этом месте стоит немного вспомнить математику. Мы говорим о частных производных функции, но при этом хотим обучить нейронную сеть, которая состоит из большого количества нейронов. При этом каждый нейрон представляет собой сложную функцию, и чтобы обновить весовые коэффициенты нейронной сети, нам необходимо посчитать частные производные сложной функции нашей нейронной сети по каждому весовому коэффициенту.
По правилам математики, производная сложной функции равна произведению частной производной внешней функции на частную производную внутренней функции.
Воспользуемся этим правилом и найдем частные производные функции потерь L по весовому коэффициенту выходного нейрона wi и по i-му входному значению xi.
где:
- L — функция потерь;
- A — функция активации нейрона;
- S — взвешенная сумма исходных данных;
- X — вектор исходных данных;
- W — вектор весовых коэффициентов;
- wi — i-ый весовой коэффициент, для которого рассчитывается производная:
- xi — i-ый элемент вектора исходных данных.
Первое, что можно заметить в представленных выше формулах, это полное совпадение первых двух множителей. Т.е. при расчете частных производных по весовым коэффициентам и исходным данным нам достаточно один раз посчитать градиент ошибки перед функцией активации, и уже используя это значение, посчитать частные производные для всех элементов векторов весовых коэффициентов и исходных данных.
Аналогичным методом определим частную производную по весовому коэффициенту одного из нейронов скрытого слоя, предшествовавшего выходному нейронному слою. Для этого в предыдущей формуле вектор исходных данных заменим функцией нейрона скрытого слоя. Вектор весовых коэффициентов обернется в скалярное значение соответствующего весового коэффициента.
где:
- Ah — функция активации нейрона скрытого слоя;
- Sh — взвешенная сумма исходных данных нейрона скрытого слоя;
- Xh — вектор исходных данных для нейрона скрытого слоя;
- Wh — вектор весовых коэффициентов нейрона скрытого слоя;
- wh — весовой коэффициент скрытого слоя, для которого рассчитывается производная.
Обратите внимание, что если в последней формуле мы вернем X вместо функции нейрона скрытого слоя, то в первых множителях функции увидим представленную выше функцию частной производной по i-му входному значению.
Отсюда,
Аналогичные формулы можно привести для каждого нейрона нашей сети. Таким образом, мы можем один раз посчитать производную и градиент ошибки на выходе нейрона, а далее распространить градиент ошибки на все связанные нейроны предыдущего слоя.
Следуя этой логике, вначале определяем отклонения от эталонного значения с помощью функции потерь. Функция потерь может быть любая, удовлетворяющая описанным в предыдущем разделе требованиям.
,
где:
- Y — вектор эталонных значений;
- Y' — вектор значений на выходе нейронной сети.
Далее мы определяем, как должны измениться состояния нейронов выходного слоя, чтобы наша функция потерь принимала минимальное значение. С математической точки зрения мы определяем градиент ошибки на каждом нейроне выходного слоя путем вычисления частной производной функции потерь по каждому параметру.
Затем мы «спускаем» градиент ошибки от выходного нейронного слоя к входному, проводя его последовательно через все скрытые нейронные слои нашей сети. Таким образом, мы как бы приводим до каждого нейрона его эталонное значение на данном шаге обучения.
где:
- gradij—1 — градиент на выходе i-го нейрона j—1 слоя;
- Akj — функция активации k-го нейрона на j-ом слое;
- Skj — взвешенная сумма входящих данных k-го нейрона на j-ом слое;
- Wkj — вектор синаптических коэффициентов k-го нейрона на j-ом слое.
После получения градиентов ошибки на выходе каждого нейрона можно приступать к корректировке синаптических коэффициентов нейронов. Для этого еще раз последовательно пройдемся через все слои нейронной сети. При этом на каждом слое будем перебирать все нейроны и для каждого нейрона будем обновлять все синаптические связи.
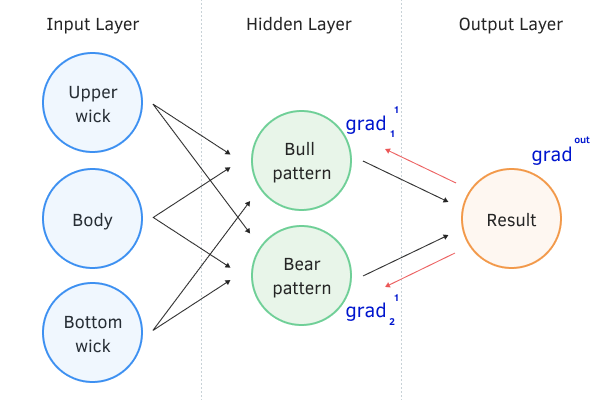
Обратный проход нейронной сети
О способах обновления весовых коэффициентов поговорим в следующей главе.
После обновления весовых коэффициентов возвращаемся к пункту 2 нашего алгоритма. Цикл повторяется до нахождения минимума функции. Определить достижение минимума можно по нулевым частным производным. В общем виде это будет заметно по отсутствию изменения ошибки на выходе нейронной сети после очередного цикла обновления весовых коэффициентов, т.к. при нулевых производных останавливается процесс обучения нейронной сети.