- Функции потерь
- Метод обратного распространения градиента ошибки
- Методы оптимизации нейронных сетей
Методы оптимизации нейронных сетей
Мы продолжаем двигаться дальше по пути изучения базовых принципов обучения нейронных сетей. В предыдущих главах мы уже рассмотрели варианты функций потерь и алгоритм обратного распространения градиента ошибки, который позволяет определить влияние каждого нейрона на общий результат и направление изменения выходного значения каждого нейрона для минимизации общей ошибки на выходе.
Напомню формулу математической модели нейрона.
где:
- f — функция активации;
- n — количество элементов во входной последовательности;
- wi — весовой коэффициент i-го элемента последовательности;
- xi — i-ый элемент входной последовательности.
Градиентный спуск и стохастический градиентный спуск #
В приведенной выше формуле видно, что выходное значение нейрона зависит от функции активации, входной последовательности и вектора весовых коэффициентов. Формула активации задается при конструировании нейронной сети и является неизменной. На входную последовательность нейрон влияние не оказывает. Следовательно, в процессе обучения изменить значение на выходе нейрона мы можем, только подобрав оптимальные значения весовых коэффициентов.
Скорость изменения выходного значения нейрона при изменении отдельно взятого весового коэффициента равна частной производной функции математической модели нейрона по данному весовому коэффициенту. Отсюда, чтобы получить дельту изменения отдельно взятого весового коэффициента, нужно умножить ошибку на выходе нейрона в текущей ситуации на частную производную математической модели нейрона по данному весовому коэффициенту.
Следует отметить, что функция математической модели нейрона чаще всего нелинейна. И, следовательно, частная производная не является постоянной на всем допустимом интервале значений. Поэтому в формулу обновления весовых коэффициентов вводится параметр «коэффициент обучения», который определяет скорость обучения.
Описанный выше подход называется градиентным спуском. В общем случае его можно выразить формулой:
где:
- wjil — l-ый весовой коэффициент на i-ом нейроне j-го слоя;
- α — обучающий коэффициент, определяющий скорость обучения;
- gradij — градиент на выходе i-го нейрона j-го слоя.
Обучающий коэффициент α является гиперпараметром, который подбирается в процессе валидации нейронной сети. Он выбирается из диапазона от 0 до 1. При этом обучающий коэффициент не может быть равен крайним значениям.
При α=0 не будет никакого обучения, так как при умножении любого градиента на ноль мы всегда получим ноль для обновления весовых коэффициентов.
При α=1 или близких к этому значению нас ждет другая проблема. Если при движении в сторону минимума ошибки значение частной производной снижается, то использование достаточно большого шага перекинет нас через точку минимума. А в худшем случае ошибка на выходе нейронной сети еще и увеличится. Кроме того, большой обучающий коэффициент способствует максимальной адаптации сети к текущей ситуации. При этом теряется способность к обобщению. Такое обучение не сможет выявить ключевые признаки и адекватно работать «в полевых условиях».
С небольшими нейронными сетями и маленькими наборами данных метод легко работает. Но нейронные сети становятся все больше, обучающие выборки растут. Для того чтобы сделать одну итерацию обучения, нужно провести прямой проход по всей выборке и сохранить информацию о состоянии всех нейронов для всех выборок — эта информация понадобится для проведения обратного прохода. Следовательно, нам потребуется дополнительное выделение памяти в размере количество нейронов * количество наборов данных.
Решение было найдено в применении стохастического градиентного спуска. Метод сохраняет алгоритм стандартного градиентного спуска, но обновление весовых коэффициентов проводится для каждого случайно взятого набора данных.
На каждой итерации из обучающей выборки случайным образом выбираем один набор данных. Далее осуществляем прямой и обратный проход и обновляем весовые коэффициенты. Затем «перемешиваем» обучающую выборку и выбираем следующий набор данных случайным образом.
Итерации повторяем до получения приемлемой ошибки на выходе нейронной сети.
Стохастический градиентный спуск обладает меньшей сходимостью, по сравнению со стандартным градиентном спуском. И, как правило, для достижения приемлемой ошибки требуется больше итераций. Но при стохастическом градиентном спуске отдельно взятая итерация требует меньше времени, поскольку осуществляется на случайно взятом наборе данных, а не на всей выборке, как при стандартном градиентном спуске. В целом процесс обучения нейронной сети осуществляется с меньшими временными и ресурсными затратами.
Ниже приведен пример реализации функции обновления весовых коэффициентов по методу градиентного спуска. В параметрах функция получает два указателя на массивы данных (текущих весовых коэффициентов и градиентов к ним) и обучающий коэффициент. Вначале проверяем соответствие размеров массивов. Затем организуем цикл, в котором для каждого элемента массива весов рассчитываем новое значение по приведенной выше формуле. Полученное значение сохраняем в соответствующей ячейке массива.
bool SGDUpdate(double &m_cWeights[], |
Метод накопления импульса (Momentum) #
Наверное, основным недостатком методов градиентного спуска является невозможность разделения локальных и глобального минимумов. В процессе обучения всегда остается большой риск остановиться в локальном минимуме, так и не достигнув желаемого уровня точности работы нейронной сети.
Тщательный подбор коэффициента обучения, эксперименты с различными вариантами инициализации весовых коэффициентов и несколько итераций обучения не всегда позволяют добиться желаемых результатов.
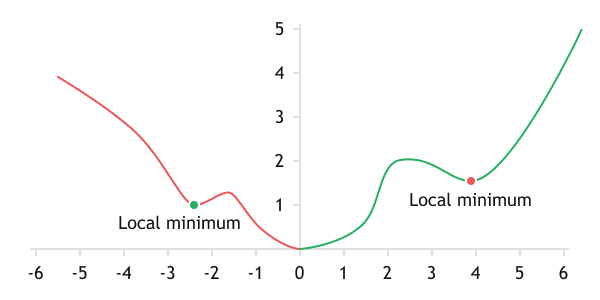
Локальные минимумы на графике сложной функции
Один из вариантов решения был заимствован из физики природных явлений. Если положить мячик в небольшое углубление или ямку, то он будет лежать без движения на ее дне. Но стоит нам тот же мячик спустить по некой наклонной поверхности в эту ямку, то он с легкостью выскочит из нее и покатится дальше. Такое поведение мячика объясняется импульсом, накопленным при спуске по наклонной поверхности.
Аналогично мячику, было предложено добавить накопление импульса при обучении весовых коэффициентов, и затем добавлять этот импульс в формулу обновления весовых коэффициентов методом градиентного спуска.
Импульсы накапливаются по каждому отдельному весовому коэффициенту. При длительном обновлении отдельно взятого весового коэффициента в одном направлении его импульс будет накапливаться и, как следствие, он будет двигаться с большей скоростью к заветной цели. Благодаря накопленной энергии мы сможем преодолевать локальные минимумы, подобно мячику, пущенному по наклонной поверхности.
К сожалению, есть и обратная сторона медали. Накапливая импульс, мы проскочим не только локальный минимум, но и глобальный. При неограниченном накоплении импульса значение нашей ошибки будет двигаться подобно маятнику по графику функции потерь. По аналогии с силой трения в природе, добавим коэффициент β в диапазоне от 0 до 1 (не включая граничные точки), который и будет выполнять роль силы трения. Данный коэффициент характеризует скорость затухания импульса. Чем ближе β к "1", тем дольше сохраняется импульс.
Все описанное выше можно записать в виде двух математических формул:
где:
- Δt — изменение весового коэффициента на текущем шаге;
- Δt—1 — изменение весового коэффициента на предыдущей итерации обучения;
- β — коэффициент затухания импульса.
В результате мы получили неплохой алгоритм для борьбы с локальными минимума. Но, к сожалению, и он не является панацеей. Для преодоления локального минимума нужно накопить достаточный импульс. Для этого инициализация должна быть на достаточной дистанции от локального минимума. При решении практических задач мы не знаем, где в действительности находятся локальные и глобальный минимумы. Да и инициализация весовых коэффициентов случайным образом может забросить нас куда угодно.
К тому же применение данного метода требует дополнительного объема памяти для хранения последнего импульса каждого нейрона и дополнительных трудозатрат на выполнение добавленных вычислений.
Все же метод накопления импульса (Momentum) используется на практике и демонстрирует лучшую сходимость, по сравнению со стохастическим градиентным спуском.
При реализации метода импульсного накопления нам потребуется добавить в параметры функции коэффициент затухания и еще один массив для хранения накопленного импульса по каждому весовому коэффициенту. Логика построения функции остается прежней: сначала проверяем корректность входных данных, а затем в цикле обновляем весовые коэффициенты. При обновлении весов, как и в приведенных формулах, вычислим сначала величину изменения синаптического коэффициента с учетом накопленного импульса, а затем его новое значение. Полученные значения сохраняем в соответствующие ячейки массивов весовых коэффициентов и моментов.
bool MomentumUpdate(double &m_cWeights[], |
//--- |
Метод адаптивного градиента (AdaGrad) #
В обоих рассмотренных выше методах присутствует гиперпараметр скорости обучения. Важно понимать, что от выбора данного параметра во многом зависит и весь процесс обучения нейронной сети. Задание слишком большой скорости обучения может привести к постоянному росту ошибки вместо ее уменьшения. Использование малой скорости обучения приведет к увеличению длительности процесса обучения и повысит вероятность застрять в локальном минимуме, даже при использовании метода накопления импульса.
Поэтому при валидации архитектуры нейронной сети очень много времени уделяется именно подбору правильного коэффициента скорости обучения. Но и при этом всегда сложно подобрать правильную скорость обучения. К тому же всегда хочется обучить нейронную сеть при минимальных затратах времени и ресурсов.
Существует практика постепенного понижения коэффициента в процессе обучения. Обучение сети начинается с относительно большим коэффициентом, который позволяет максимально быстро спуститься до некоторого уровня ошибки. После понижения коэффициента обучения проводится более тонкая подстройка весовых коэффициентов нейронной сети для понижения общей ошибки. Итераций с понижением коэффициента может быть несколько, но с каждым понижением весового коэффициента уменьшается эффективность данной итерации.
Здесь стоит обратить внимание еще и на тот момент, что мы используем одну скорость обучения для всех нейронных слоев и нейронов. Но не все признаки и нейроны вносят одинаковый вклад в финальный результат нейронной сети, поэтому наш коэффициент скорости обучения должен быть довольно универсальным.
Думаю, не стоит говорить, что универсальность враг лучшего: при создании любого универсального продукта или подбора значения (как в нашем случае) приходится идти на компромиссы, чтобы максимально удовлетворить все предъявляемые требования. А эти требования часто бывают противоречивыми.
Казалось бы, в таком случае следует предложить индивидуальные коэффициенты обучения для нейронов. Но решение этой задачи ручным трудом практически невыполнимо. В 2011 году был предложен метод адаптивного градиента AdaGrad. Предложенный метод является вариацией от рассмотренного выше градиентного спуска и не исключает использование коэффициента скорости обучения. При этом авторы метода предлагают накапливать сумму квадратов градиентов за все предшествующие итерации и при обновлении весовых коэффициентов делить обучающий коэффициент на квадратный корень из накопленной суммы квадратов градиентов.
где:
- Gt , Gt—1 — сумма квадратов градиентов на текущем и предыдущем шаге, соответственно;
- ε — некое малое положительное число, чтобы исключить деление на ноль.
Таким образом мы получаем индивидуальный для каждого нейрона и постоянно уменьшающийся коэффициент скорости обучения. Как всегда, за это нам приходится платить дополнительными ресурсами на вычисления и выделением дополнительного объема памяти для хранения сумм квадратов градиентов.
Функция реализации метода AdaGrad очень похожа на функцию обновления весовых коэффициентов методом накопленного импульса. В ней мы отказываемся от использования коэффициента затухания, но по-прежнему используем массив моментов. Только теперь мы будем в него складывать накопленную сумму квадратов градиентов. Также изменения коснулись и вычисления нового значения весового коэффициента. Полный код функции приведен ниже.
bool AdaGradUpdate(double &m_cWeights[], |
//--- |
В приведенной выше формуле можно заметить и основную проблему данного метода. Мы постоянно накапливаем сумму квадратов градиентов. Как следствие, на достаточно длинной обучающей выборке наши скорости обучения быстро будут стремиться к нулю. Это приведет к параличу нейронной сети и невозможности дальнейшего обучения.
Выход из сложившейся ситуации был предложен в методе RMSProp.
Метод RMSProp #
Метод обновления весовых коэффициентов RMSProp является логическим продолжением метода AdaGrad. В нем сохраняется идея автоматического регулирования скорости обучения в зависимости от частоты обновления и величины градиентов, поступающих на нейрон, но при этом решается основная проблема рассмотренного выше метода — паралич обучения на больших тренировочных выборках.
Как и AdaGrad, метод RMSProp эксплуатирует сумму квадратов градиентов, но в RMSProp применяется экспоненциально сглаженная средняя квадратов градиентов.
где:
- REMS(G)t , REMS(G)t—1 — экспоненциальная средняя квадратов градиентов на текущей и предыдущей итерации;
- γ — коэффициент экспоненциального сглаживания.
Использование экспоненциально сглаженной средней квадратов градиентов позволяет избежать снижения скорости обучения нейронов до нуля. При этом каждый весовой коэффициент получит индивидуальную скорость обучения, зависящую от поступающих градиентов. С ростом градиентов скорость обучения будет постепенно снижаться, а при снижении градиентов коэффициент скорости обучения будет нарастать. Это позволит в первом случае ограничить максимальную скорость обучения, а во втором — обновлять коэффициенты даже при малых градиентах ошибки.
Следует обратить внимание, что использование квадрата градиента позволяет работать данному методу и в том случае, когда на нейрон поступают разнонаправленные градиенты. Если из-за большого обучающего коэффициента в процессе обучения мы будем перескакивать через минимум и на следующей итерации двигаться в противоположном направлении, накопленный квадрат градиентов будет постепенно снижать коэффициент обучения, тем самым позволяя нам спуститься ближе к минимуму ошибки.
Реализация данного подхода практически полностью повторяет реализацию метода адаптивного градиента. Мы лишь заменим расчет суммы квадратов градиентов на их экспоненциальную среднюю. Для этого нам потребуется дополнительный параметр γ.
bool RMSPropUpdate(double &m_cWeights[], |
//--- |
Метод Adadelta #
В методах AdaGrad и RMSProp мы дали индивидуальный коэффициент обучения каждому нейрону, но по-прежнему оставили гиперпараметр скорости обучения в числителе формулы. Создатели метода Adadelta пошли немного дальше и предложили полностью отказаться от данного гиперпараметра. В математической формуле метода Adadelta его место заняла экспоненциальная средняя изменений весовых коэффициентов за предыдущие итерации.
где:
- REMS(δw)t , REMS(δw)t—1 — экспоненциальная средняя квадратов изменений весовых коэффициентов на текущей и предыдущей итерации.
В практике применения данного метода могут встречаться как одинаковые коэффициенты экспоненциального сглаживания квадратов дельт весовых коэффициентов и градиентов, так и индивидуальные. Решение принимает архитектор нейронной сети.
Ниже дается пример реализации метода средствами MQL5. Логика построения алгоритма полностью повторяет представленные выше функции. Изменения коснулись лишь вычислений, являющихся особенностями метода: отказ от коэффициента обучения и ввод дополнительного коэффициента усреднения, а вместе с ним и еще одного массива данных.
bool AdadeltaUpdate(double &m_cWeights[], |
//--- |
Метод адаптивной оценки моментов #
В 2014 году Diederik P. Kingma и Jimmy Lei Ba предложили метод адаптивной оценки моментов Adam. По словам авторов, метод объединяет преимущества методов AdaGrad и RMSProp и хорошо работает при онлайн-обучении. Данный метод показывает стабильно хорошие результаты на разных выборках и в последнее время рекомендуется к применению по умолчанию в различных пакетах.
В основе метода лежит расчет экспоненциальной средней градиента m и экспоненциального среднего квадратов градиента v. Каждая экспоненциальная средняя имеет свой гиперпараметр ß, определяющий период усреднения.
Авторы предлагают использовать по умолчанию ß1 на уровне 0,9 и ß2 на уровне 0,999. При этом m0 и v0 принимают нулевые значения. С такими параметрами формулы, представленные выше, в начале обучения возвращают значения близкие к нулю. Как следствие, мы получаем низкую скорость обучения на начальном этапе. Для ускорения обучения авторы предложили скорректировать полученные моменты.
Обновление параметров осуществляется путем корректировки на отношение скорректированного момента градиента m к корню квадратному из скорректированного момента квадрата градиента v. Для исключения деления на ноль в знаменатель добавляют близкую к нулю константу ε. Полученное отношение корректируется на коэффициент обучения α, который в данном случае выступает верхней границей шага обучения. По умолчанию авторы предлагают использовать α на уровне 0,001.
Реализация метода Adam немного сложнее представленных выше, но в целом выдержана в той же логике. Изменения видны только в теле цикла обновления весовых коэффициентов.
bool AdamUpdate(double &m_cWeights[], |
w -= learningRate * m / (MathSqrt(v) + 1.0e-10); |