Функции потерь
Приступая к обучению, необходимо определиться с методами определения качества обучения сети. Обучение нейронной сети — это итерационный процесс. На каждой итерации нам необходимо определить, насколько расчеты нейронной сети точны. В случае обучения с учителем — на сколько они отличаются от эталона. Только зная отклонение, мы сможем понять, насколько и в какую сторону нам нужно корректировать синаптические коэффициенты.
Следовательно, нам нужна некая метрика, которая непредвзято и с математической точностью покажет погрешность работы нейронной сети.
На первый взгляд, это довольно тривиальная задача — сравнить два числа (расчетное значение нейронной сети и целевое). Но, как правило, на выходе нейронной сети мы получаем не одно значение, а целый вектор. Для решения этой задачи обратимся к математической статистике. Введем некую функцию потерь, которая зависит от расчетного значения (y') и эталонного (y).
Данная функция должна определить отклонение расчетного значения от эталонного (ошибку). Если рассматривать расчетное и эталонное значения как точки в пространстве, то ошибка является расстоянием между этими точками. Следовательно, функция потерь при всех допустимых значениях должна быть непрерывной и неотрицательной.
В идеальном состоянии расчетное и эталонное значения совпадают, расстояние между точками равно нулю. Следовательно, функция должна быть выпуклой вниз с минимумом в L(y,y')=0.
В книге Л. Б. Клебанова "Robust and Non-Robust Models in Statistics" описано четыре свойства, которыми должна обладать функция потерь:
- Полнота информации;
- Отсутствие условия рандомизации;
- Условие симметризации;
- Состояние Рао-Блэквелла (статистические оценки параметров могут быть улучшены).
В книге приводится довольно много математических теорем и их доказательств. Демонстрируется взаимосвязь между выбором функции потерь и статистической оценкой. Как следствие, некоторые статистические проблемы могут быть решены при правильном выборе функции потерь.
Средняя абсолютная ошибка (MAE) #
Одну из первых функций потерь — среднюю абсолютную ошибку (в английской аббревиатуре MAE) — представил французский математик 18-го века Пьер-Симон де Лаплас. Он предложил для оценки отклонения использовать модуль разницы между эталонным и расчетным значениями.
Функция имеет график, симметричный относительно нуля, линейный до и после нуля.
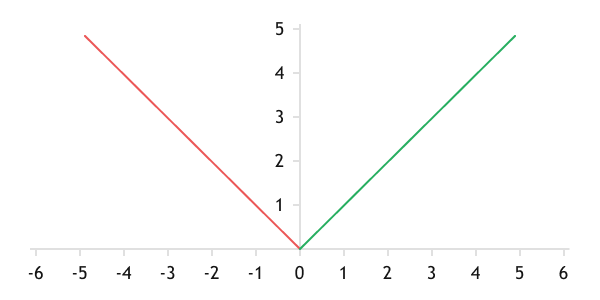
График функции среднего абсолютного отклонения
Использование среднего абсолютного отклонения дает линейное приближение аналитической функции к обучающей выборке на всей дистанции ошибки.
Посмотрим на вариант реализации данной функции в программном коде MQL5. Для расчета отклонений функция должна получить на вход два вектора данных: расчетных и эталонных значений. Эти данные будем передавать в параметрах функции.
В начале метода сравним размеры полученных массивов. В идеале размеры массивов должны быть не меньше нуля. Если проверка не пройдена, то выйдем из функции с результатом максимально возможной ошибки DBL_MAX.
double MAE(double &calculated[], double &target[]) |
После успешного прохождения проверок организуем цикл для суммирования абсолютных значений отклонений. В заключение разделим полученную сумму на количество эталонных значений.
//--- |
Среднеквадратичная ошибка (MSE) #
Немецкий математик 19-го века Карл Фридрих Гаусс предложил в формуле среднего абсолютного отклонения вместо модуля отклонения использовать его квадрат. Функция получила название среднеквадратичного отклонения.
Благодаря квадрату отклонения функция ошибки приобретает вид параболы.
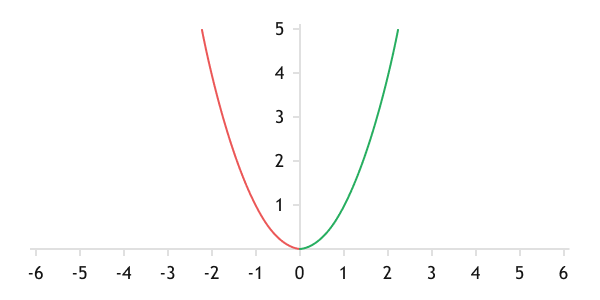
График функции среднеквадратичного отклонения
При использовании среднеквадратичного отклонения скорость компенсации ошибки тем выше, чем больше сама ошибка. При снижении ошибки падает и скорость ее компенсации. В случае с нейронными сетями это позволяет быстрее сходиться нейронной сети при больших ошибках и проводить более тонкую настройку при малых ошибках.
Но есть и обратная сторона медали: указанное выше свойство делает функцию чувствительной к шумовым явлением, так как редкое, большое отклонение вызывает смещение функции.
В настоящее время использование среднеквадратичной ошибки в качестве функции потерь широко используется при решении задач регрессии.
Алгоритм реализации MSE на MQL5 аналогичен реализации MAE. Отличие лишь в теле цикла, где вычисляется сумма квадратов отклонений вместо их абсолютных значений.
double MSE(double &calculated[], double &target[]) |
//--- |
Кросс-энтропия #
Для решения задач классификации в качестве функции потерь чаще всего используют функцию кросс-энтропии.
Энтропия — это мера неопределенности в распределении.
Применение энтропии переводит расчеты из плоскости абсолютных значений в область вероятностей. Кросс-энтропия определяет сходство вероятностей проявления событий двух распределений и вычисляется по формуле:
где:
- p(yi) — вероятность появления i-го события в эталонном распределении;
- p(yi') — вероятность появления i-го события в расчетном распределении.
Так как мы исследуем вероятности появления событий, то значение вероятностей появления события всегда лежит в диапазоне значений от 0 до 1. Значение логарифма в данном диапазоне отрицательное, поэтому добавление знака минуса перед функцией переводит значение функции в положительную область и делает функцию строго убывающей. Для наглядности график логарифмической функции представлен ниже.
В процессе обучения для событий эталонного распределения при появлении события его вероятность равна единице. Вероятность появления отсутствующего события равна нулю. Исходя из графика функции, наибольшую ошибку будет генерировать событие, произошедшее в эталонном распределении и не предсказанное аналитической функцией. Таким образом, мы будем стимулировать нейронную сеть к предсказанию ожидаемых событий.
Именно применение вероятностной модели делает эту функцию наиболее привлекательной для решения задач классификации.
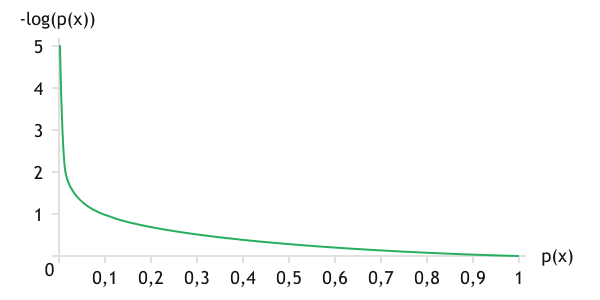
График функции логарифма
Вариант реализации данной функции представлен ниже. Алгоритм реализации аналогичен двум предыдущим функциям.
double LogLoss(double &calculated[], double &target[]) |
Выше представлено описание лишь трех наиболее часто используемых функций потерь. Но на самом деле их число значительно больше. И тут, как и в случае функций активации, нам помогут векторные и матричные операции, реализованные в языке MQL5, среди которых реализована функция Loss. Данная функция позволяет одной строкой кода вычислить функцию потерь между двумя векторами/матрицами одинакового размера. Функция вызывается для вектора или матрицы расчетных значений. В параметрах функции передаются вектор/матрица эталонных значений и тип функции потерь.
double vector::Loss( |
double matrix::Loss( |
Разработчики компании MetaQuotes реализовали 14 различных функций потерь. Их список представлен в таблице ниже.
Идентификатор |
Описание |
|---|---|
LOSS_MSE |
Среднеквадратичная ошибка |
LOSS_MAE |
Средняя абсолютная ошибка |
LOSS_CCE |
Категориальная кросс-энтропия |
LOSS_BCE |
Бинарная кросс-энтропия |
LOSS_MAPE |
Средняя абсолютная ошибка в процентах |
LOSS_MSLE |
Среднеквадратичная логарифмическая ошибка |
LOSS_KLD |
Дивергенция Кульбака-Лейблера |
LOSS_COSINE |
Косинусное сходство/близость |
LOSS_POISSON |
Функция потерь Пуассона |
LOSS_HINGE |
Кусочно-линейная функция потерь (Hinge loss) |
LOSS_SQ_HINGE |
Квадратичная кусочно-линейная функция потерь |
LOSS_CAT_HINGE |
Категориальная кусочно-линейная функция потерь |
LOSS_LOG_COSH |
Логарифм гиперболического косинуса |
LOSS_HUBER |
Функция потерь Хьубера |