[Архив!] Чистая математика, физика, химия и т.п.: задачки для тренировки мозгов, никак не связанные с торговлей - страница 14
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
Ну мне сказать тут нечего, увы. :(
Ну мне сказать тут нечего, увы. :(
про компас? - это же шутка, думал, что под ваш "психотип" подойдет. :о)
Алексей, тебя мое решение устраивает ?
Думаешь для 7-го это слишком круто (не общий, а частный случай 25 одноклассников) ?
Да, для 7-го, пожалуй, крутовато. Но элементарно, и это радует.
Yurixx писал(а) >> Два элемента должны иметь одинаковые значения.
Нетрудно проверить, что при N=26 (т.е. в классе отсутствует ученик с нулем связей) это повторяющееся число = 13.
Единственное, что мне непонятно, - это почему 13, а не 14 или 2. Ты со своей процедурой последовательной разметки мне весь мосх размягчил - но, наверно, именно в ней следует искать объяснение, почему именно 13 :)
Ты, кстати, использовал принцип Дирихле, не называя его.
А почему так?
хороший вопрос)
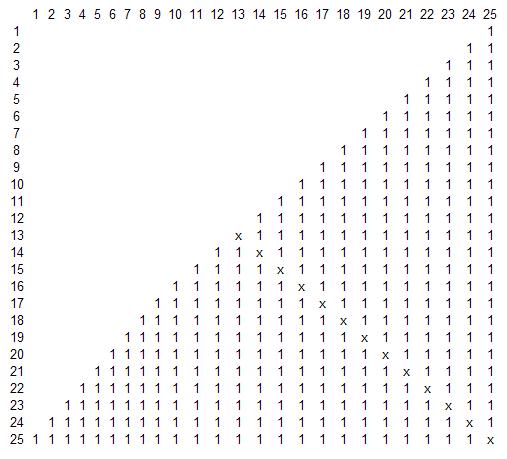
картинка такая(от 1 до 25)
диагональ xxx, никто сам с собой не дружит, приходится этим заниматься Пете и таки видно шо тринадцать раз))
в случае от ноля до 24, можно одного однокласника не учитывать получим квадрат 24*24 и 12 иксов.
при нечётном размере квадрата диагональ=(N+1)/2, при чётном N/2.
Можно представить это как разницу дружбоф) в классе с учётом Пети и без него.
Не похоже на строгое доказательство. Это скорее иллюстрация на пальцах без указания ясных причин, почему именно 12 или 13. ОК, будем думать.
Единственное, что мне непонятно, - это почему 13, а не 14 или 2. Ты со своей процедурой последовательной разметки мне весь мосх размягчил - но, наверно, именно в ней следует искать объяснение, почему именно 13 :)
Ты, кстати, использовал принцип Дирихле, не называя его.
Дело в том, что при этой разметке (а она подчиняется только одному принципу - у всех разное число друзей, и потому достаточно общая) Петя вообще не участвует. Он является одним из 26 учеников, абсолютно равноправным с остальными. В результате получается, что у всех не может быть разное число друзей - ряд от 1 до N-1 невозможно пронумеровать последовательно N разными числами (это в финале доказательства). Поэтому у двух учеников количество друзей должно совпадать. И эти два ученика находятся рядом в центре ряда. Так и получается, что Петя должен быть одним из этих двух. Только в этом случае все остальные имеют разное число друзей. Любые другие разметки не смогут удовлетворить этому условию.
Если попробуешь руками разметить в центре, то сам все увидишь.
Таблица Swan'а это и иллюстрирует.
Надеюсь я правильно понял твой вопрос.
По-моему я не использовал принцип Дирихле, а предложил элементарное доказательство его частного случая.
Мне лично понравилось.
Изящно.
Напомнило басню про проворного маленького Гаусса и учителя который задал классу задачу сложить числа от 1 до 99 и собирался свалить на некоторое время - пока детки будут складывать.
Умножение они уже знали, но повторение - мать учения...
Гаусс обломал учителя - ответ получен был сразу.
;)
Swetten у нас самая дружелюбная.
:)
В коллективе из N сотрудников не может быть ситуации когда у каждого разное количество друзей
А вот если добавить - "у двух возможно одинаковое количество друзей" тогда нет проблем
Остается обозвать Петей одного из этих двух
Да, это почти так.
Если читать условие задачи ЮРИДИЧЕСКИ - то у Пети МОЖЕТ быть равное с одним другим число друзей.
Я же говорил - эта задача некорректна - при ЛЮБОМ прочтении условий. Я пожалуй могу ДОКАЗАТЬ это, причём разными способами. Но не буду..... пока.