Роль качества генератора случайных чисел в эффективности алгоритмов оптимизации

Введение

Когда речь идет о применении алгоритмов оптимизации, многих читателей статей интересует, насколько важно использовать высококачественный генератор случайных чисел. Ответ на этот вопрос не так прост, как может показаться на первый взгляд. Однако интуитивно понятно, что качество случайных чисел может оказать значительное влияние на поисковые возможности алгоритмов, поскольку популяционные алгоритмы в подавляющем своем большинстве основаны на стохастическом поиске.

Давайте вместе разберемся в этом вопросе, но прежде, чем приступить, познакомимся с различными типами генераторов случайных чисел, их влиянием на результаты и где можно найти надежные варианты.

Генераторы случайных чисел (СЧ) — это алгоритмы или устройства, которые создают последовательность чисел или значений и числа кажутся случайными. Важно отметить, что в компьютерных науках и математике такие последовательности обычно называются "псевдослучайными", так как они генерируются детерминированными алгоритмами, а не истинно случайными процессами.

Существует два основных типа генераторов случайных чисел:

1. Псевдослучайные генераторы (ПСГ). Эти генераторы используют математические формулы или алгоритмы для создания последовательности чисел, которые кажутся случайными. Они инициализируются начальным значением, известным как "зерно" (seed), и каждый раз, когда генератор вызывается, он выдает следующее число в последовательности. При правильном выборе алгоритма и зерна ПСГ могут быть полезны для многих приложений, где требуется псевдослучайная последовательность.
2. Истинные генераторы случайных чисел (ИГС). Эти генераторы используют истинно случайные процессы, такие как шум радиоактивного распада или шум квантовых явлений, для создания случайных чисел. Такие генераторы обычно используются в криптографии, лотереях и других областях, где требуется высокая степень случайности.

В программировании часто используются генераторы псевдослучайных чисел, такие как генераторы, встроенные в стандартные библиотеки языков программирования.

Точность генераторов случайных чисел, встроенных в языки программирования, зависит от конкретной реализации и алгоритма, который используется для генерации случайных чисел. Большинство современных языков программирования, такие как MQL5, Python, C++, C#, Java и другие предоставляют встроенные генераторы псевдослучайных чисел, которые обеспечивают достаточно хорошее качество случайных чисел для большинства обычных приложений.

В целом, встроенные генераторы случайных чисел в языках программирования обычно подходят для большинства обычных задач, но для задач, где требуется высокий уровень случайности или безопасности, стоит обратить внимание на специализированные решения.

Для задач, где требуется высокий уровень случайности и безопасности, могут использоваться специализированные решения для генерации случайных чисел. Некоторые из таких решений включают в себя:

1. Криптографические генераторы случайных чисел. Эти генераторы предназначены для использования в криптографических приложениях, где требуется высокий уровень безопасности. Они обеспечивают случайность, устойчивость к предсказанию и стойкость к криптоанализу.
2. Аппаратные генераторы случайных чисел. Эти генераторы используют физические процессы, такие как тепловой шум или квантовые явления, для создания случайных чисел. Они обеспечивают истинно случайные числа и широко применяются в областях, где требуется высокая степень случайности.
3. Библиотеки для генерации случайных чисел. Существуют специализированные библиотеки, которые предоставляют более сложные алгоритмы для генерации случайных чисел, чем стандартные встроенные генераторы в языках программирования. Например, библиотека OpenSSL предоставляет криптографические функции, включая генерацию случайных чисел.

Некоторые из наиболее распространенных алгоритмов, которые могут использоваться во встроенных генераторах случайных чисел в языках программирования, включают в себя:

1. Линейный конгруэнтный метод (Linear Congruential Generator, LCG). Это один из наиболее простых и широко используемых алгоритмов для генерации псевдослучайных чисел. Он имеет недостатки, такие как короткий период и низкая степень случайности.
2. Мерсенн-Твистер (Mersenne Twister). Этот алгоритм обладает длинным периодом и хорошей степенью случайности, и он часто используется во многих языках программирования.
3. Xorshift. Это семейство алгоритмов генерации псевдослучайных чисел, которые обладают хорошей степенью случайности и высокой скоростью работы.
4. PCG (Permuted Congruential Generator). Этот относительно новый класс генераторов обладает хорошим балансом между качеством случайности и производительностью.

Выбор генератора случайных чисел зависит от конкретных требований ваших задач. Несколько соображений, которые могут помочь принять решение:

1. Качество случайности. Если ваше приложение требует высокого уровня случайности, особенно в криптографических целях, то лучше всего использовать специализированные криптографические генераторы случайных чисел, такие как Cryptographically Secure Pseudo-Random Number Generators (CSPRNGs).
2. Производительность. Если для вас важна скорость генерации случайных чисел, то алгоритмы с более высокой производительностью, такие как Xorshift или PCG, могут быть предпочтительны.
3. Период и качество. Некоторые алгоритмы, такие как Вихрь Мерсенна, обладают длинным периодом и хорошим качеством случайности.
4. Удобство использования. Для некоторых разработчиков важно, чтобы генератор случайных чисел был легко доступен и прост в использовании. Встроенные генераторы, такие как те, которые предоставляются стандартными библиотеками языков программирования, могут быть удобными в таких случаях.

Если вам необходим криптографический уровень безопасности, рекомендуется использовать специализированные криптографические генераторы случайных чисел, такие как CryptoRandom в Python или SecureRandom в Java. Если вам нужен баланс между производительностью и качеством случайности, то алгоритмы, такие как Вихрь Мерсенна или PCG, могут быть хорошими вариантами.

Важно также помнить, что безопасность и случайность играют ключевую роль в обеспечении надежности и безопасности системы, поэтому выбор генератора должен быть обдуманным и соответствовать требованиям конкретной задачи. Но в данной статье нас интересует влияние качества ГСЧ на результаты работы алгоритмов оптимизации, и мы будем проводить исследование исключительно в этом контексте.

Вихрь Мерсенна

Среди множества доступных генераторов случайных чисел непросто найти такой, который обеспечивает высокое качество генерации, сохраняя при этом приемлемую скорость. Ведь скорость генерации имеет существенное влияние на общее время выполнения процесса оптимизации.

Поэтому выбор надежного генератора является важным вопросом, требующим баланса между качеством случайных чисел и их скоростью генерации. Необходимо найти оптимальное решение, которое обеспечит достаточное качество генерации, не затрачивая излишнее время на этот процесс.

Аппаратные генераторы труднодоступны для большинства пользователей, поэтому мы их сразу отбрасываем из претендентов на объект рассмотрения в статье. Из программных генераторов имеет широкую известность качественный генератор Мерсенна.

Вихрь Мерсенна (Mersenne Twister) — это алгоритм генерации псевдослучайных чисел, который был разработан Макото Мацумото и Такэши Нишимурой в 1997 году. Он является одним из наиболее широко используемых алгоритмов генерации случайных чисел благодаря своей хорошей комбинации длинного периода, хорошего качества случайности и относительно высокой производительности.

Основные характеристики Вихря Мерсенна:

• Длинный период. Вихрь Мерсенна обладает очень длинным периодом, что означает, что он может генерировать огромное количество уникальных псевдослучайных чисел перед тем, как начнет повторяться последовательность.
• Хорошее качество случайности. Алгоритм обеспечивает хорошее качество случайности, что означает, что сгенерированные числа должны соответствовать статистическим свойствам случайных чисел.
• Производительность. Вихрь Мерсенна имеет хорошую производительность, что делает его привлекательным выбором для многих задач.

Принцип работы Вихря Мерсенна основан на линейном рекуррентном методе генерации псевдослучайных чисел. Алгоритм использует большое число (обычно 32-битное или 64-битное) в качестве состояния генератора, который затем преобразуется с помощью сложных операций, чтобы получить следующее псевдослучайное число. В нашем случае мы будем использовать 64-битный генератор.

Рассмотрим класс "MersenneTwister64", который реализует генератор псевдослучайных чисел на основе алгоритма Mersenne Twister для 64-битных чисел. Краткое описание его методов и функциональности:

• Init - Метод инициализации генератора случайных чисел. Принимает в качестве аргумента seed (начальное значение) и устанавливает внутренние переменные класса. Заполняет массив MT (мерсеннский массив) значениями, основываясь на seed.
• RND_ulong - Метод, возвращающий случайное 64-битное беззнаковое целое число. Если текущий индекс (index) превышает 312, вызывается метод twist() для обновления значений в массиве MT. Затем выполняются несколько операций побитового сдвига и побитового исключающего ИЛИ для получения случайного числа. Значение индекса увеличивается на 1 перед возвратом результата.
• RND_ulong_In_Range - Метод, возвращающий случайное 64-битное беззнаковое целое число в заданном диапазоне (включая границы). Если min и max равны, возвращается min. Если min больше max, значения min и max меняются местами. Затем вызывается метод RND_ulong() для генерации случайного числа, которое смещается и масштабируется для попадания в заданный диапазон.
• twist - Внутренний метод, который выполняет операцию "перемешивания" массива MT. Для каждого элемента массива происходит комбинация соседних элементов с использованием побитовых операций сдвига и побитового исключающего ИЛИ. Значение индекса устанавливается в 0 после выполнения операции "перемешивания".

//——————————————————————————————————————————————————————————————————————————————
class MersenneTwister64
{
public: //--------------------------------------------------------------------

  void Init (ulong seed)
  {
    index = 312;

    MT [0] = seed;
    for (int i = 1; i < 312; i++)
    {
      MT [i] = (6364136223846793005 * (MT [i - 1] ^ (MT [i - 1] >> 62)) + i) & 0xFFFFFFFFFFFFFFFF;
    }
  }

  //from 0 to 18 446 744 073 709 551 615
  ulong RND_ulong ()
  {
    if (index >= 312)
    {
      twist ();
    }

    ulong y = MT [index];
    y = y ^ (y >> 29) & 0x5555555555555555;
    y = y ^ (y << 17) & 0x71D67FFFEDA60000;
    y = y ^ (y << 37) & 0xFFF7EEE000000000;
    y = y ^ (y >> 43);

    index++;
    return y;
  }

  ulong RND_ulong_In_Range (ulong min, ulong max)
  {
    if (min == max) return min;
    if (min > max)
    {
      ulong temp = min;
      min = max;
      max = temp;
    }
    return min + RND_ulong () % (max - min + 1);
  }

private: //-------------------------------------------------------------------
  ulong MT [312];
  int index;

  void twist ()
  {
    for (int i = 0; i < 312; i++)
    {
      ulong y = (MT [i] & 0x8000000000000000) + (MT [(i + 1) % 312] & 0x7FFFFFFFFFFFFFFF);
      MT [i] = MT [(i + 156) % 312] ^ (y >> 1);
      if (y % 2 != 0)
      {
        MT [i] = MT [i] ^ 0xB5026F5AA96619E9;
      }
    }
    index = 0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Сравнение генераторов случайных чисел и результаты тестирования

Попробуем визуально сравнить работу двух генераторов случайных чисел: встроенного в MQL5 (в дальнейшем будем называть его "стандартный") и Вихря Мерсенна. Для этого мы сгенерировали два изображения и проанализировали их внешний вид. На первый взгляд, оба изображения лишены закономерностей и периодичности, а их рисунок является гомогенным. Визуально мы не наблюдаем явных отличий между генераторами.

Изображение сгенерировано стандартным генератором.

Изображение сгенерировано генератором Вихрь Мерсенна.

Однако для более объективного сравнения генераторов случайных чисел, рекомендуется использовать статистические тесты, которые позволяют оценить степень случайности и статистические свойства сгенерированных чисел. Важно отметить, что визуальная оценка может быть ограничена и не всегда способна выявить скрытые систематические отклонения от истинной случайности.

Таким образом, для более точного сравнения генераторов проведем дополнительный анализ с помощью статистического теста, чтобы получить более надежные результаты. Нас интересует равномерность, поэтому будем использовать тест на хи-квадрат, который является статистическим тестом и позволяет оценить, насколько равномерными являются случайные сгенерированные числа. В данном случае было проведено 10000 наблюдений, каждое из которых содержало 10000 сгенерированных значений.

Тест хи-квадрат (χ²-тест) используется для проверки равномерности распределения данных. Он позволяет определить, насколько наблюдаемые частоты соответствуют ожидаемым в равномерном распределении.

Критическое значение для уровня значимости 0.05 в тесте хи-квадрат (χ²-тест) с 9999 степенями свободы (10000 наблюдений минус 1) составляет 10232.73727. Это значение является константой, которая используется для сравнения ожидаемых частот с наблюдаемыми в хи-квадрат тесте. Оно взято из таблицы хи-квадрат распределения и помогает определить, насколько значимы различия между наблюдаемыми и ожидаемыми значениями.

Когда мы проводим тест хи-квадрат, мы сравниваем рассчитанную статистику с критическим значением. Если рассчитанная статистика больше критического значения, мы можем отвергнуть нулевую гипотезу, что распределение согласуется с ожидаемым. В противном случае нулевая гипотеза принимается.

Посмотрим на участок кода тестового скрипта (в целом скрипт строит изображения, замеряет время выполнения генераторов и рассчитывает тест хи-квадрат).

Создаются и инициализируются два массива: "observed" и "expected". Массив "observed" будет использоваться для сохранения наблюдаемого количества выпадения случайных чисел в каждом из "BoxesNumber" интервалов. Массив "expected" будет содержать ожидаемое количество выпадений случайных чисел в каждом интервале, если генераторы работали бы с идеальным равномерным распределением.

Затем код проверяет значение переменной "StandardRND", которая указывает, какой генератор случайных чисел использовать. Если "StandardRND" равно true, то используется стандартный генератор случайных чисел в MQL5. В противном случае используется генератор Вихря Мерсенна. В цикле генерируются случайные числа и увеличивается соответствующий элемент массива "observed" для интервала.

После генерации случайных чисел выполняется вычисление статистики хи-квадрат. Для каждого интервала вычисляется значение "(наблюдаемое - ожидаемое)^2 / ожидаемое" и суммируется в переменную "chiSquareStatistic". Затем задается критическое значение "chiSquareCriticalValue" для уровня значимости 0.05*.

В конце кода выводятся результаты сравнения. Если значение "chiSquareStatistic" больше "chiSquareCriticalValue", то выводится сообщение, что мы отвергаем нулевую гипотезу: распределение отличается от ожидаемого. В противном случае выводится сообщение, что мы не отвергаем нулевую гипотезу: распределение согласуется с ожидаемым.

* - Уровень значимости 0.05 (или 5%) является одним из наиболее распространенных уровней значимости и широко используется во многих областях научных исследований. Это означает, что при проведении статистического теста с уровнем значимости 0.05 мы допускаем 5% вероятность ошибки первого рода. Уровень значимости (significance level) в статистике является пороговым значением, которое используется для принятия решений о статистической значимости результатов. Он обычно обозначается как α (альфа) и представляет собой вероятность ошибки первого рода, то есть вероятность отвергнуть верную нулевую гипотезу.

int observed [];
ArrayResize     (observed, BoxesNumber);
ArrayInitialize (observed, 0);

int expected [];
ArrayResize     (expected, BoxesNumber);
ArrayInitialize (expected, ThrowsNumber / BoxesNumber);

if (StandardRND)
{
  Print ("Standard, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [rndS.RNDintInRange (0, BoxesNumber - 1)]++;
  }
}
else
{
  Print ("Mersenne, ", ThrowsNumber, " throws, ", BoxesNumber, " boxes");
  for (int i = 0; i < ThrowsNumber; i++)
  {
    observed [(int)rndM.RND_ulong_In_Range (0, BoxesNumber  - 1)]++;
  }
}

// Вычисление статистики хи-квадрат
double chiSquareStatistic = 0;
for (int i = 0; i < ArraySize(observed); i++)
{
  chiSquareStatistic += MathPow(observed[i] - expected[i], 2) / expected[i];
}

// Критическое значение для уровня значимости 0.05
double chiSquareCriticalValue = 10232.73727; //10000

// Вывод результатов
if (chiSquareStatistic > chiSquareCriticalValue)
{
  Print("We reject the null hypothesis: The distribution differs from the expected one.");
}
else
{
  Print("We do not reject the null hypothesis: The distribution is consistent with the expected one.");
}

Запустим скрипт 5 раз для расчета статистики и времени выполнения стандартного генератора. Заодно выполняется замер времени выполнения генератора Вихрь Мерсенна. Вычисляем разницу по времени выполнения как частное времени выполнения Вихря и времени выполнения стандартного генератора.

2024.03.18 20:54:33.456    stand: 120353 mcs
2024.03.18 20:54:33.456    mers : 397920 mcs
2024.03.18 20:54:33.456    diff : 3.3062740438543283
2024.03.18 20:54:33.459    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:33.854    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:38.802    stand: 121670 mcs
2024.03.18 20:54:38.802    mers : 403180 mcs
2024.03.18 20:54:38.802    diff : 3.3137174323991125
2024.03.18 20:54:38.805    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:39.194    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:43.767    stand: 121222 mcs
2024.03.18 20:54:43.767    mers : 400986 mcs
2024.03.18 20:54:43.767    diff : 3.3078649090099157
2024.03.18 20:54:43.770    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:44.156    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:48.476    stand: 119246 mcs
2024.03.18 20:54:48.476    mers : 400319 mcs
2024.03.18 20:54:48.476    diff : 3.3570853529678146
2024.03.18 20:54:48.479    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:48.873    We reject the null hypothesis: The distribution differs from the expected one.
2024.03.18 20:54:53.144    stand: 119309 mcs
2024.03.18 20:54:53.144    mers : 404502 mcs
2024.03.18 20:54:53.144    diff : 3.390372897266761
2024.03.18 20:54:53.148    Standard, 100000000 throws, 10000 boxes
2024.03.18 20:54:53.553    We reject the null hypothesis: The distribution differs from the expected one.

К сожалению, стандартный генератор случайных чисел, не прошел ни одного из пяти испытаний при проверке с помощью теста на хи-квадрат, что указывает на наличие систематических отклонений от ожидаемого случайного равномерного распределения.

Теперь проведём испытание Вихря Мерсенна, при этом, продолжая, замерять время выполнения у обоих генераторов.

2024.03.18 20:55:48.133    stand: 115447 mcs
2024.03.18 20:55:48.133    mers : 413258 mcs
2024.03.18 20:55:48.133    diff : 3.57963394458063
2024.03.18 20:55:48.138    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:49.504    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:55:56.340    stand: 117433 mcs
2024.03.18 20:55:56.340    mers : 402337 mcs
2024.03.18 20:55:56.340    diff : 3.4260982858310696
2024.03.18 20:55:56.346    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:55:57.717    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:05.837    stand: 120129 mcs
2024.03.18 20:56:05.837    mers : 400705 mcs
2024.03.18 20:56:05.837    diff : 3.3356225391037966
2024.03.18 20:56:05.843    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:07.219    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:12.206    stand: 119980 mcs
2024.03.18 20:56:12.206    mers : 397436 mcs
2024.03.18 20:56:12.206    diff : 3.312518753125521
2024.03.18 20:56:12.211    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:13.582    We do not reject the null hypothesis: The distribution is consistent with the expected one.
2024.03.18 20:56:18.837    stand: 118140 mcs
2024.03.18 20:56:18.837    mers : 397565 mcs
2024.03.18 20:56:18.837    diff : 3.3652023023531403
2024.03.18 20:56:18.842    Mersenne, 100000000 throws, 10000 boxes
2024.03.18 20:56:20.220    We do not reject the null hypothesis: The distribution is consistent with the expected one.

Вихрь Мерсенна справился с задачей на всех пяти тестах (запусков теста хи-квадрат). При этом видим, что у этого генератора есть существенный недостаток - Вихрь медленнее стандартного примерно в 3.4 раза, что может заметно повлиять на скорость работы алгоритмов оптимизации.

Настало время самого интересного - изюминки данного исследования: проведём испытания с целью выяснить, насколько сильно влияет качество генераторов случайных чисел на результаты оптимизации. Напомню, что стандартный генератор создаёт числа в диапазоне [0;32767], а 64-битный Вихрь Мерсена в диапазоне [0;18446744073709551615].

Для проведения эксперимента мы выбрали 50 функций Hilly и выполнили 10 000 итераций для каждой функции. Почему мы выбрали именно 50 функций Hilly и почему именно Hilly? Во-первых, это количество было выбрано таким образом, чтобы алгоритм не смог достичь 100% сходимости за ограниченное количество запусков фитнес-функции. Это позволило наблюдать разницу в применении различных типов генераторов случайных чисел. Во-вторых, выбор функций Hilly обусловлен её гладкостью, что позволяет избежать закономерного разброса результатов, не связанного с генерацией случайных чисел, если бы мы применили дискретную тестовую функцию. Мы повторили эксперимент 20 раз и усреднили результаты для получения более надежных и статистически значимых данных. В качестве алгоритма оптимизации мы выбрали BGA, который занимает первое место в нашей рейтинговой таблице и при этом демонстрирует очень малый разброс результатов на гладких функциях.

Из распечатки результатов видно, что результаты оптимизации при использовании как стандартного генератора случайных чисел, так и генератора Мерсенна практически одинаковы для алгоритма BGA. Различия наблюдаются только в третьем знаке после запятой, которые не являются критическими для наших целей и считаются достаточно малыми.

//Standard
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9257245560389498
=============================
All score: 0.92572

//Mersenne
C_AO_BGA:50:50:1.0:3:0.001:0.7:16
=============================
50 Hilly's; Func runs: 10000; result: 0.9221148477644971
=============================
All score: 0.92211

При визуализации работы алгоритма мы не обнаружили значительных отклонений при использовании двух различных типов генераторов случайных чисел внутри логики алгоритма, а разница в разбросах результатов вполне укладывается в вариабельность работы самого алгоритма.

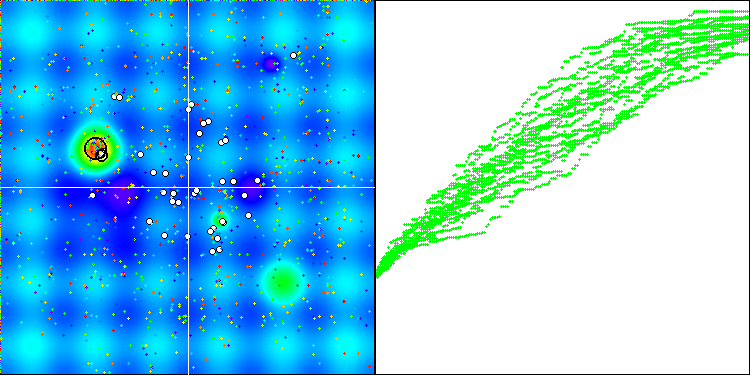
Работа BGA со стандартным генератором. 

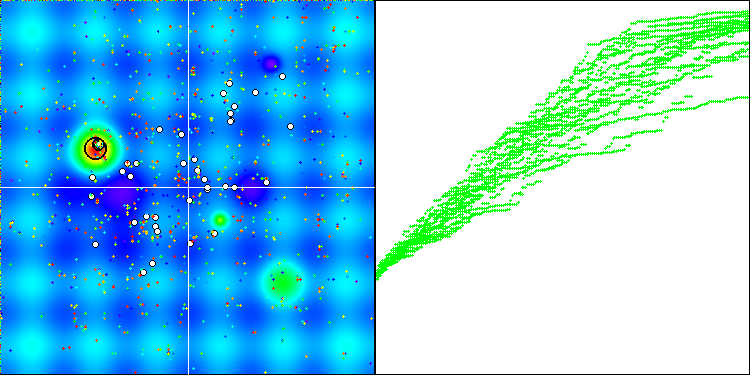
Работа BGA с Вихрем Мерсенна.

Предварительный вывод такой: качество генераторов случайных чисел не влияет на работу алгоритмов оптимизации.

Сделаем предположение, что незначительная разница в результатах при применении выше озвученных генераторов в алгоритме оптимизации BGA возможно связана с тем, что в BGA каждый бит в хромосоме генерируется независимо от остальных битов. По сути, роль генераторов случайных сводится к булевой операции, "да/нет", а разница между количеством выпадений "да" и "нет" хоть и существует, но составляет всего лишь тысячные доли процента.

Хорошо, для бинарного генетического алгоритма нет никакой разницы в использовании генераторов случайных чисел, хотя этот вывод был вовсе не очевиден на первый взгляд, но так ли это для других алгоритмов оптимизации, особенно для тех, которые используют непрерывные вероятности на всём протяжении пространства, ограниченного границами [min, max] по координатам?

Тогда попробуем провести еще несколько экспериментов, чтобы закрепить полученное утверждение или опровергнуть его, в этот раз возьмем алгоритм (P_O)ES, алгоритм находится в числе лидеров нашей рейтинговой таблицы и использует в своей логике большое количество операций со случайными числами и использует непрерывные вероятности на всём пространстве поиска.

Распечатка работы (P_O)ES в 5 запусках тестов со стандартным генератором СЧ:

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9611258962207798
=============================
All score: 0.96113

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9515388684155862
=============================
All score: 0.95154

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9374143219597522
=============================
All score: 0.93741

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9408961932771648
=============================
All score: 0.94090

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9533447716768805
=============================
All score: 0.95334

Распечатка работы (P_O)ES в 5 запусках тестов с генератором Вихря Мерсенна:

C_AO_(P_O)ES:100:150:0.02:8.0:10

=============================
50 Hilly's; Func runs: 10000; result: 0.9726583883537465
=============================
All score: 0.97266

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9699307111435692
=============================
All score: 0.96993

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9864631937799934
=============================
All score: 0.98646

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9608040257741147
=============================
All score: 0.96080

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
50 Hilly's; Func runs: 10000; result: 0.9540192199550924
=============================
All score: 0.95402

Как можно увидеть из распечатки проведенных экспериментов, первая серия опытов относилась к использованию в алгоритме стандартного генератора случайных чисел. Мы видим, что среднее значение результата находится в области 0.95, а среднее значение результата при использовании Вихря Мерсенна составляет 0.96, что не дает существенной разницы, однако показывает нам, что все же результаты проведенных экспериментов выше при участии Вихря Мерсенна, но необходимо помнить, что время затраченное при использовании данного алгоритма превышает время работы стандартного алгоритма в 3.5 раза.

Выводы

Итак, мы провели интересный эксперимент с целью поставить точку в вопросе, волнующим многих: важно ли качество генераторов случайных чисел в применении совместно с алгоритмами оптимизации. Подобного исследования я не встречал в свободном доступе.

Для некоторым алгоритмов, которые используют булевые операции, таких как BGA, и алгоритмов, использующих случайные числа в небольшом дискретном диапазоне, таких ка DE (дифференциальная эволюция, где случайные числа используются для выбора родительских особей в популяции), качество ГСЧ не играет практически никакой роли.

Для других алгоритмов, использующих случайные числа для генерации новых решений во всем диапазоне оптимизируемых параметров, такие как (P_O)ES (к подобным относится большинство популяционных алгоритмов) качество ГСЧ хоть и играет роль, но оно очень незначительно и укладывается в погрешность измерений. Важно, что более качественный генератор Вихрь Мерсенна в 3.5 раза медленнее стандартного.

В задачах оптимизации баланс качества и времени вычислений играет, безусловно, важную роль в конечном итоге, в данном случае мы выбираем скорость. Прирост результатов алгоритмов от применения качественных генераторов находится в пределах погрешности измерений, при этом скорость падает в разы.

К статье прикреплен архив с кодами проведённых тестов. Выводы и суждения, представленные в статье, основываются на результатах проведённых экспериментов.