
Нейросети — это просто (Часть 53): Декомпозиция вознаграждения
Введение
Мы продолжаем рассмотрение методов обучения с подкреплением. Как Вы знаете, все алгоритмы обучения моделей данного направления машинного обучения основаны на парадигме максимизации вознаграждения от окружающей среды. И функция вознаграждения играет ключевую роль в процессе обучения моделей. Очень редко её сигналы однозначны.
В попытках стимулирования Агента к желаемому поведению мы вводим в функцию вознаграждения дополнительные премии и штрафы. К примеру, мы часто усложняли функцию вознаграждения в попытке стимулировать Агента к изучению окружающей среды и вводили штрафы за бездействие. При этом архитектура модели и функция вознаграждения остаются плодом субъективных соображений архитектора модели.
В процессе обучения модель может столкнуться с различными сложностями и трудностями, даже при тщательном подходе к проектированию. Агент может не достичь желаемых результатов по множеству различных причин, поиск которых превращается в "гадание на кофейной гуще". Но как понять, что Агент правильно трактует наши сигналы в функции вознаграждения? В попытке разобраться с этим вопросом возникает желание разделить вознаграждение на отдельные составляющие. Использование декомпозированного вознаграждения и анализ влияния отдельных компонентов могут быть очень полезны в поиске путей оптимизации процесса обучения модели. Это позволит лучше понять, как различные аспекты влияют на поведение Агента. Выявить причины проблем и эффективно скорректировать архитектуру модели, процесс обучения или функцию вознаграждения.
1. Необходимость декомпозиции вознаграждения
Декомпозиции значений функции вознаграждений простой и широко применимый метод, который может справиться с различными вызовами. В обучении с подкреплением Агент получает вознаграждение, которое часто представляет собой сумму множества компонент. Каждая из них предназначена для кодирования некоторого аспекта желаемого поведения Агента. Из этого композитного вознаграждения Агент обучается единственной сложной функции ценности. Используя декомпозицию значений, Агент учит функции ценности для каждой компоненты вознаграждения. И любая отдельно взятая из них функция вероятнее будет иметь более простую форму.
Для целей оптимизации стратегии композитная функция ценности восстанавливается путем взвешенной суммы функций ценности компонент.
Декомпозицию вознаграждений можно включить в широкий спектр различных методов, в том числе и рассматриваемое нами семейство методов Актер-Критик.
Однако, дополнительные диагностические и обучающие возможности декомпозиции функции вознаграждения имеют свою цену в виде более сложной задачи прогнозирования: вместо обучения одной функции ценности необходимо обучить множество функций. Анализ влияния данного фактора на производительность Агента проведен в статье "Value Function Decomposition for Iterative Design of Reinforcement Learning Agents". Авторы статьи обнаружили, что при добавлении декомпозиции функции вознаграждения в алгоритм Soft Actor-Critic результаты обучения модели уступают исходному алгоритму. Однако, авторы предложили варианты улучшения алгоритма. Что позволило не только соответствовать исходному алгоритму Soft Actor-Critic, но иногда и превосходить его производительность. Эти улучшения могут быть применены к декомпозиции функции вознаграждения и для других алгоритмов семейства Актер-Критик.
Широкий спектр алгоритмов обучения с подкреплением может быть адаптирован для использования декомпозиции функции вознаграждения по следующему шаблону:
- Изменяем модель Q-функций, чтобы на выходе модели мы получили по одному элементу для каждой компоненты функции вознаграждения.
- Используем базовый алгоритм обучения Q-функции для обновления каждой компоненты.
Этот шаблон работает для алгоритмов обучения моделей как с дискретным, так и непрерывным пространством действий.
Идея довольно проста. Но как было сказано выше, авторы статьи обнаружили неэффективности "решения в лоб" при использовании декомпозиции вознаграждения в рамках алгоритма Soft Actor-Critic. Напомню формулы оптимизации Q-функции в данном алгоритме.
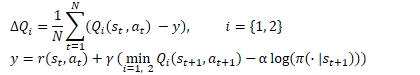
Здесь мы видим использование минимальной оценки будущего состояния из 2 целевых моделей Критиков. Как указано в пункте 2 шаблона, для обновления параметров каждой компоненты Q-функции мы используем базовый алгоритм. Но как показала практика, использование покомпонентного минимального значения ведет к разбалансированию модели. Более эффективно работает выбор одной модели с минимальной общей оценкой. И использование её оценок компонент для обучения моделей.
В целом предполагается, что функция вознаграждения модели является линейной функцией её компонент.
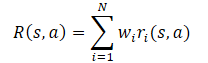
Применяя линейность математического ожидания, мы находим, что Q-функция наследует линейную структуру от функции вознаграждения.
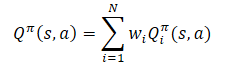
Если не оговорено иное, мы предполагаем, что Wi=1 для всех i. И поскольку веса компонентов вынесены из Q-функции, то их можно изменять без изменения целевого прогноза компоненты. Это позволяет оценивать политику для любой комбинации весов.
Второй момент, на который стоит обратить внимание, оптимизация декомпозированной функции вознаграждения — это оптимизация модели по многим критериям. И ей присущи проблемы, характерные для многокритериальной оптимизации: конфликтующие градиенты, высокая кривизна и большие различия в величинах градиентов. Для минимизации отрицательного влияния данного фактора, авторы метода предлагают использовать алгоритм Conflict-Averse Gradient Descent (CAGrad), разработанный для среды многозадачного обучения с подкреплением. Этот метод направлен на смягчение вышеуказанных проблем многокритериальной оптимизации. Основная идея заключается в том, чтобы заменить градиент многозадачной целевой функции на взвешенную сумму градиентов для каждой отдельной задачи. Для этого решается следующая оптимизационная задача:
![]()
где d — вектор обновления,
g₀ — средний градиент,
с — коэффициент скорости сходимости в диапазоне [0, 1).
Решение данной оптимизационной задачи позволяет учитывать влияние каждой компоненты на оптимизацию и делать акцент на улучшение наихудшей оценки на каждом шаге.
2. Реализация средствами MQL5
2.1 Создание нового класса модели
Свой вариант декомпозиции функции вознаграждения мы реализуем на базе алгоритма SAC+DICE. Сразу скажем, что ввиду особенностей реализации алгоритмов, мы не будем наследоваться от класса CNet_SAC_DICE, созданного в предыдущей статье. Но все же мы воспользуемся ранее сделанным наработками. Мы создадим по его образу и подобию новый класс CNet_SAC_D_DICE, структура которого приведена ниже.
class CNet_SAC_D_DICE : protected CNet { protected: CNet cActorExploer; CNet cCritic1; CNet cCritic2; CNet cTargetCritic1; CNet cTargetCritic2; CNet cZeta; CNet cNu; CNet cTargetNu; vector<float> fLambda; vector<float> fLambda_m; vector<float> fLambda_v; int iLatentLayer; float fCAGrad_C; int iCAGrad_Iters; int iUpdateDelay; int iUpdateDelayCount; //--- float fLoss1; float fLoss2; vector<float> fZeta; vector<float> fQWeights; //--- vector<float> GetLogProbability(CBufferFloat *Actions); vector<float> CAGrad(vector<float> &grad); public: //--- CNet_SAC_D_DICE(void); ~CNet_SAC_D_DICE(void) {} //--- bool Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1); //--- virtual bool Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau); virtual void GetLoss(float &loss1, float &loss2) { loss1 = fLoss1; loss2 = fLoss2; } virtual bool TargetsUpdate(float tau); //--- virtual void SetQWeights(vector<float> &weights) { fQWeights=weights; } virtual void SetCAGradC(float c) { fCAGrad_C=c; } virtual void SetLambda(vector<float> &lambda) { fLambda=lambda; fLambda_m=vector<float>::Zeros(lambda.Size()); fLambda_v=fLambda_m; } virtual void TargetsUpdateDelay(int delay) { iUpdateDelay=delay; iUpdateDelayCount=delay; } //--- virtual bool Save(string file_name, bool common = true); bool Load(string file_name, bool common = true); };
В приведенной структуре класса мы видим заимствованные объекты моделей. Но вместо переменных для хранения коэффициента Лагранжа и его средних мы будем использовать вектора, размер которых равен количеству компонент функции вознаграждения. Тут же мы добавляем вектор fQWeights для хранения весовых коэффициентов каждой компоненты. Переменную fCAGrad_C выделим для записи коэффициента скорости сходимости метода CAGrad.
И вполне естественно, что данные изменения нашли свое отражение в конструкторе класса. На начальном этапе мы инициализируем все вектора единичной длины.
CNet_SAC_D_DICE::CNet_SAC_D_DICE(void) : fLoss1(0), fLoss2(0), fCAGrad_C(0.5f), iCAGrad_Iters(15), iUpdateDelay(100), iUpdateDelayCount(100) { fLambda = vector<float>::Full(1, 1.0e-5f); fLambda_m = vector<float>::Zeros(1); fLambda_v = vector<float>::Zeros(1); fZeta = vector<float>::Zeros(1); fQWeights = vector<float>::Ones(1); }
Метод инициализации класса и создания вложенных моделей практически полностью перекочевал из прошлой статьи. Изменения внесены лишь в части изменения размеров векторов.
bool CNet_SAC_D_DICE::Create(CArrayObj *actor, CArrayObj *critic, CArrayObj *zeta, CArrayObj *nu, int latent_layer = -1) { ResetLastError(); //--- if(!cActorExploer.Create(actor) || !CNet::Create(actor)) { PrintFormat("Error of create Actor: %d", GetLastError()); return false; } //--- if(!opencl) { Print("Don't opened OpenCL context"); return false; } //--- if(!cCritic1.Create(critic) || !cCritic2.Create(critic)) { PrintFormat("Error of create Critic: %d", GetLastError()); return false; } //--- if(!cZeta.Create(zeta) || !cNu.Create(nu)) { PrintFormat("Error of create function nets: %d", GetLastError()); return false; } //--- if(!cTargetCritic1.Create(critic) || !cTargetCritic2.Create(critic) || !cTargetNu.Create(nu)) { PrintFormat("Error of create target models: %d", GetLastError()); return false; } //--- cActorExploer.SetOpenCL(opencl); cCritic1.SetOpenCL(opencl); cCritic2.SetOpenCL(opencl); cZeta.SetOpenCL(opencl); cNu.SetOpenCL(opencl); cTargetCritic1.SetOpenCL(opencl); cTargetCritic2.SetOpenCL(opencl); cTargetNu.SetOpenCL(opencl); //--- if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), 1.0) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), 1.0) || !cTargetNu.WeightsUpdate(GetPointer(cNu), 1.0)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- cZeta.getResults(fZeta); ulong size = fZeta.Size(); fLambda = vector<float>::Full(size,1.0e-5f); fLambda_m = vector<float>::Zeros(size); fLambda_v = vector<float>::Zeros(size); fQWeights = vector<float>::Ones(size); iLatentLayer = latent_layer; //--- return true; }
Обратите внимание, что здесь мы инициализируем вектор весов fQWeights единичными значениями. Если Ваша функция вознаграждения предусматривает иные коэффициенты, то необходимо воспользоваться методом SetQWeights. Однако, вызывать его надо уже после инициализации класса методом Create, иначе Ваши коэффициенты будут перезаписаны единичными значениями.
Алгоритм Conflict-Averse Gradient Descent мы вынесли в отдельный метод CAGrad. В параметрах данный метод получает вектор градиентов и возвращает скорректированный вектор.
В теле метода мы сначала проведем небольшую подготовительную работу, в которой:
- определим среднее значение градиента;
- масштабируем градиенты для повышения стабильности вычислений;
- подготовим локальные переменные и вектора.
vector<float> CNet_SAC_D_DICE::CAGrad(vector<float> &grad) { matrix<float> GG = grad.Outer(grad); GG.ReplaceNan(0); if(MathAbs(GG).Sum() == 0) return grad; float scale = MathSqrt(GG.Diag() + 1.0e-4f).Mean(); GG = GG / MathPow(scale,2); vector<float> Gg = GG.Mean(1); float gg = Gg.Mean(); vector<float> w = vector<float>::Zeros(grad.Size()); float c = MathSqrt(gg + 1.0e-4f) * fCAGrad_C; vector<float> w_best = w; float obj_best = FLT_MAX; vector<float> moment = vector<float>::Zeros(w.Size());
После завершения подготовительной работы мы организуем цикл решения оптимизационной задачи. В теле цикла мы итерационно решаем задачу нахождения оптимального вектора обновления с помощью метода градиентного спуска.
for(int i = 0; i < iCAGrad_Iters; i++) { vector<float> ww; w.Activation(ww,AF_SOFTMAX); float obj = ww.Dot(Gg) + c * MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f); if(MathAbs(obj) < obj_best) { obj_best = MathAbs(obj); w_best = w; } if(i < (iCAGrad_Iters - 1)) { float loss = -obj; vector<float> derev = Gg + GG.MatMul(ww) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2) + ww.MatMul(GG) * c / (MathSqrt(ww.MatMul(GG).Dot(ww) + 1.0e-4f) * 2); vector<float> delta = derev * loss; ulong size = delta.Size(); matrix<float> ident = matrix<float>::Identity(size, size); vector<float> ones = vector<float>::Ones(size); matrix<float> sm_der = ones.Outer(ww); sm_der = sm_der.Transpose() * (ident - sm_der); delta = sm_der.MatMul(delta); if(delta.Ptp() != 0) delta = delta / delta.Ptp(); moment = delta * 0.8f + moment * 0.5f; w += moment; if(w.Ptp() != 0) w = w / w.Ptp(); } }
После завершения итераций цикла мы корректируем градиенты ошибки с использованием оптимальных весовых коэффициентов. Полученный результат возвращаем вызывающей программе.
w_best.Activation(w,AF_SOFTMAX); float gw_norm = MathSqrt(w.MatMul(GG).Dot(w) + 1.0e-4f); float lmbda = c / (gw_norm + 1.0e-4f); vector<float> result = ((w * lmbda + 1.0f / (float)grad.Size()) * grad) / (1 + MathPow(fCAGrad_C,2)); //--- return result; }
Весь процесс обучения, как и в классе CNet_SAC_DICE, мы организовали в методе CNet_SAC_D_DICE::Study. Но несмотря на единство подходов и внешнее сходство, в алгоритме и структуре метода есть много отличий. И первые изменения мы внесли в параметры метода. Здесь мы заменили переменную вознаграждения reward на вектор декомпозированных вознаграждений Rewards.
Кроме того, мы исключили вектор логарифмов вероятностей действий ActionsLogProbab. Как Вы знаете, алгоритмом Soft Actor-Critic энтропийная составляющая включается в функцию вознаграждения для стимулирования Агента к повторному совершению действий с малой вероятностью. А декомпозиция функции вознаграждения выделяет отдельный элемент для каждого компонента. Таким образом, логарифмы вероятности уже присутствуют в векторе декомпозированного вознаграждения Rewards и нам нет необходимости их дублировать в отдельном векторе.
bool CNet_SAC_D_DICE::Study(CArrayFloat *State, CArrayFloat *SecondInput, CBufferFloat *Actions, vector<float> &Rewards, CBufferFloat *NextState, CBufferFloat *NextSecondInput, float discount, float tau) { //--- if(!Actions) return false;
В теле метода мы проверяем актуальность указателя на полученный буфер выполненных действий. И на этом завершается контрольный блок нашего метода.
Переходя к следующему этапу, надо сказать, что в процессе обучения модели был замечен довольно большой необоснованный рост оценок последующих состояний целевыми моделями. Подобные оценки сильно превышали фактические вознаграждения, что приводило к взаимной адаптации обучаемой модели и её целевой копии без учета фактических вознаграждений окружающей среды.
Для минимизации этого эффекта было принято решение на начальном этапе обучать модель с использование фактического накопительного вознаграждения. Полный отказ от использования целевых моделей так же имеет отрицательный эффект. Ведь в буфере воспроизведения опыта накопительная оценка ограничена обучающим периодам. Она может сильно отличаться для подобных состояний и действий в зависимости от расстояния до конца обучающей выборки. Это сглаживается целевой моделью. Кроме того, целевая модель помогает оценить состояния с учетом действий текущей политики. С ростом количество итераций обновления параметров Агента текущая политика все больше будет отличаться от политики в буфере воспроизведения опыта, что нельзя игнорировать. Но нужна целевая модель с адекватными оценками. Таким образом, нам нужно 2 режима работы метода: с использование целевых моделей и без.
В процессе организации алгоритма метода мы руководствуемся следующими соображениями:
- При необходимости использования целевых моделей пользователь передает в параметрах указатели на будущие состояния. В векторе Rewards содержится декомпозированное вознаграждение только за действие, совершенное в текущем состоянии.
- При отказе от использования целевых моделей пользователь не передает указатели на будущие состояния (в переменных параметров содержится NULL). В векторе Rewards содержится накопительное декомпозированное вознаграждение.
Следовательно, далее мы проверяем указатель на будущее состояние и, при необходимости, определяем действие в будущем состоянии с учетом текущей политики. И оцениваем пару состояние-действие.
if(!!NextState) if(!CNet::feedForward(NextState, 1, false, NextSecondInput)) return false; if(!cTargetCritic1.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1) || !cTargetCritic2.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false; //--- if(!cTargetNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this), layers.Total() - 1)) return false;
Далее мы совершаем прямой проход консервативной политики в текущем состоянии. Осуществляем подмену действий и проводим прямой проход моделей DICE блока.
if(!CNet::feedForward(State, 1, false, SecondInput)) return false; CBufferFloat *output = ((CNeuronBaseOCL*)((CLayer*)layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite(); if(!cNu.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false; if(!cZeta.feedForward(GetPointer(this), iLatentLayer, GetPointer(this))) return false;
После чего определим значения функций потерь моделей блока Distribution Correction Estimation. Данный шаг был подробно описан в предыдущей статье. Я лишь акцентирую внимание, что в случае отказа от использования целевой модели вектор оценки будущего состояния next_nu заполняется нулевыми значениями.
vector<float> nu, next_nu, zeta, ones; cNu.getResults(nu); cZeta.getResults(zeta); if(!!NextState) cTargetNu.getResults(next_nu); else next_nu = vector<float>::Zeros(nu.Size()); ones = vector<float>::Ones(zeta.Size()); vector<float> log_prob = GetLogProbability(output); int shift = (int)(Rewards.Size() - log_prob.Size()); if(shift < 0) return false; float policy_ratio = 0; for(ulong i = 0; i < log_prob.Size(); i++) policy_ratio += log_prob[i] - Rewards[shift + i] / LogProbMultiplier; policy_ratio = MathExp(policy_ratio / log_prob.Size()); vector<float> bellman_residuals = (next_nu * discount + Rewards) * policy_ratio - nu; vector<float> zeta_loss = MathPow(zeta, 2.0f) / 2.0f - zeta * (MathAbs(bellman_residuals) - fLambda) ; vector<float> nu_loss = zeta * MathAbs(bellman_residuals) + MathPow(nu, 2.0f) / 2.0f; vector<float> lambda_los = fLambda * (ones - zeta);
Далее мы обновляем вектор коэффициентов Лагранжа с использованием метода оптимизации Adam.
Обратите внимание, что вектор градиентов ошибок мы корректируем с использование выше рассмотренного метода CAGrad. А использование векторных операций нам позволяет работать с векторами также просто, как и с простыми переменными.
Скорректированные значения мы сохраним в соответствующем векторе.
vector<float> grad_lambda = CAGrad((ones - zeta) * (lambda_los * (-1.0f))); fLambda_m = fLambda_m * b1 + grad_lambda * (1 - b1); fLambda_v = fLambda_v * b2 + MathPow(grad_lambda, 2) * (1.0f - b2); fLambda += fLambda_m * lr / MathSqrt(fLambda_v + lr / 100.0f);
Следующим этапом мы обновляем параметры моделей v, ζ. Алгоритм данных операций остается прежним. Мы лишь заменяем переменные на вектора и используем векторные операции.
CBufferFloat temp; temp.BufferInit(MathMax(Actions.Total(), SecondInput.Total()), 0); temp.BufferCreate(opencl); //--- update nu int last_layer = cNu.layers.Total() - 1; CLayer *layer = cNu.layers.At(last_layer); if(!layer) return false; CNeuronBaseOCL *neuron = layer.At(0); if(!neuron) return false; CBufferFloat *buffer = neuron.getGradient(); if(!buffer) return false; vector<float> nu_grad = CAGrad(nu_loss * (zeta * bellman_residuals / MathAbs(bellman_residuals) - nu)); if(!buffer.AssignArray(nu_grad) || !buffer.BufferWrite()) return false; if(!cNu.backPropGradient(output, GetPointer(temp))) return false;
Векторы градиентов ошибки мы обязательно корректируем с использованием алгоритма Conflict-Averse Gradient Descent в методе CNet_SAC_D_DICE::CAGrad.
//--- update zeta last_layer = cZeta.layers.Total() - 1; layer = cZeta.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; vector<float> zeta_grad = CAGrad(zeta_loss * (zeta - MathAbs(bellman_residuals) + fLambda) * (-1.0f)); if(!buffer.AssignArray(zeta_grad) || !buffer.BufferWrite()) return false; if(!cZeta.backPropGradient(output, GetPointer(temp))) return false;
На этом этапе мы завершаем работу с объектами блока Distribution Correction Estimation и переходим к процедуре обучения наших моделей Критиков. Вначале мы осуществляем их прямой проход. Прямой проход Актера мы уже осуществили ранее.
//--- feed forward critics if(!cCritic1.feedForward(GetPointer(this), iLatentLayer, output) || !cCritic2.feedForward(GetPointer(this), iLatentLayer, output)) return false;
Следующим этапом нам предстоит определить вектор эталонных значений для обновления параметров Критиков. Здесь есть 2 момента. И оба они касаются целевых моделей. Вначале мы проверяем необходимость их использования для оценки последующего состояния и действия. Для этого мы проверяем указатель на последующее состояние системы.
Если мы все же используем целевые модели для оценки последующей пары состояние-действие, то нам необходимо выбрать целевого Критика с минимальной совокупной оценкой. Совокупную оценку легко получить путем умножения вектора весовых коэффициентов компонент функции вознаграждения на вектор декомпозированного прогнозного вознаграждения, полученного при прямом проходе целевых моделей. Далее нам остается лишь выбрать минимальную оценку и сохранить вектор прогнозных значений выбранной модели.
При отказе от оценки последующих состояний вектор прогнозных значений заполняется нулевыми значениями.
vector<float> result; if(fZeta.CompareByDigits(vector<float>::Zeros(fZeta.Size()),8) == 0) fZeta = MathAbs(zeta); else fZeta = fZeta * 0.9f + MathAbs(zeta) * 0.1f; zeta = MathPow(MathAbs(zeta), 1.0f / 3.0f) / (MathPow(fZeta, 1.0f / 3.0f) * 10.0f); vector<float> target = vector<float>::Zeros(Rewards.Size()); if(!!NextState) { cTargetCritic1.getResults(target); cTargetCritic2.getResults(result); if(fQWeights.Dot(result) < fQWeights.Dot(target)) target = result; }
Прогнозные оценки корректируем на коэффициент дисконтирования и суммируем с вознаграждением текущего состояния.
target = (target * discount + Rewards); ulong total = log_prob.Size(); for(ulong i = 0; i < total; i++) target[shift + i] = log_prob[i] * LogProbMultiplier;
В полученном векторе мы скорректируем логарифм вероятности действий в текущей политике. Здесь стоит отметить, что логарифмы вероятностей действий, сохраненные в буфере воспроизведения опыта, уже содержатся в векторе вознаграждений. Мы же заменяем их значения логарифмов текущей политики, чтобы обучить критика оценке с учетом текущей политике.
После определения целевых значений мы вычисляем ошибку прогнозирования первого Критика и градиент ошибки по каждому компоненту Q-функции. Полученные градиенты корректируем с использованием алгоритма Conflict-Averse Gradient Descent.
//--- update critic1 cCritic1.getResults(result); vector<float> loss = zeta * MathPow(result - target, 2.0f); if(fLoss1 == 0) fLoss1 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss1 = MathSqrt(0.999f * MathPow(fLoss1, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); vector<float> grad = CAGrad(loss * zeta * (target - result) * 2.0f);
Скорректированные градиенты ошибки мы переносим в соответствующий буфер Критика1 и осуществляем обратный проход модели.
last_layer = cCritic1.layers.Total() - 1; layer = cCritic1.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic1.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
Здесь же мы осуществляем частичный обратный проход Актера, для корректировки блока предварительной обработки исходных данных.
Повторяем операции для второго Критика.
//--- update critic2 cCritic2.getResults(result); loss = zeta * MathPow(result - target, 2.0f); if(fLoss2 == 0) fLoss2 = MathSqrt(fQWeights.Dot(loss) / fQWeights.Sum()); else fLoss2 = MathSqrt(0.999f * MathPow(fLoss2, 2.0f) + 0.001f * fQWeights.Dot(loss) / fQWeights.Sum()); grad = CAGrad(loss * zeta * (target - result) * 2.0f); last_layer = cCritic2.layers.Total() - 1; layer = cCritic2.layers.At(last_layer); if(!layer) return false; neuron = layer.At(0); if(!neuron) return false; buffer = neuron.getGradient(); if(!buffer) return false; if(!buffer.AssignArray(grad) || !buffer.BufferWrite()) return false; if(!cCritic2.backPropGradient(output, GetPointer(temp)) || !backPropGradient(SecondInput, GetPointer(temp), iLatentLayer)) return false;
В следующем блоке нашего метода мы будем осуществлять обновление политик. Напомню, что алгоритмом SAC+DICE предусмотрено обучение 2 политик Актеров: консервативной и оптимистической. Вначале мы осуществим обновление консервативной политики. Прямой проход для данной модели мы уже осуществили ранее.
Для обучения Актеров мы будем использовать Критика с минимальной средней ошибкой. Определим такую модель и сохраним на неё указатель в локальной переменной.
vector<float> mean; CNet *critic = NULL; if(fLoss1 <= fLoss2) { cCritic1.getResults(result); cCritic2.getResults(mean); critic = GetPointer(cCritic1); } else { cCritic1.getResults(mean); cCritic2.getResults(result); critic = GetPointer(cCritic2); }
Тут же мы загрузим прогнозные оценки каждого из Критиков. После чего определим эталонные значения для обратного прохода моделей по формуле.
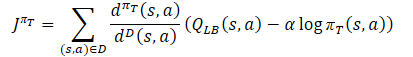
При этом мы обязательно корректируем вектор градиентов ошибки с использованием метода Conflict-Averse Gradient Descent.
vector<float> var = MathAbs(mean - result) / 2.0f; mean += result; mean /= 2.0f; target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target - var * 2.5f) - result) + result;
Далее нам остается перенести полученные данные в буфер и осуществить обратный проход Критика и Актера. Чтобы исключить взаимную подстройку моделей, перед началом операций отключаем режим обучения Критика. В данном случае мы используем его только для передачи градиента ошибки Актеру.
CBufferFloat bTarget; bTarget.AssignArray(target); critic.TrainMode(false); if(!critic.backProp(GetPointer(bTarget), GetPointer(this)) || !backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; }
Модель оптимистического Актера, в отличии от консервативного, ранее мы еще не использовали. Следовательно, перед началом процесса обновления его параметров нам предстоит осуществить её прямой проход с текущим состоянием окружающе среды.
//--- update exploration policy if(!cActorExploer.feedForward(State, 1, false, SecondInput)) { critic.TrainMode(true); return false; } output = ((CNeuronBaseOCL*)((CLayer*)cActorExploer.layers.At(layers.Total() - 1)).At(0)).getOutput(); output.AssignArray(Actions); output.BufferWrite();
Как и в случае консервативного Актера, мы осуществляем подмену вектора действий и получаем логарифмы вероятностей, но уже с учетом оптимистической политики.
cActorExploer.GetLogProbs(log_prob);
И определим вектор эталонных значений для обратного прохода моделей, но уже по формуле оптимистической политики.
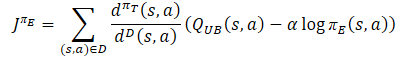
Вектор градиентов ошибок корректируем методом Conflict-Averse Gradient Descent.
target = mean; for(ulong i = 0; i < log_prob.Size(); i++) target[shift + i] = discount * log_prob[i] * LogProbMultiplier; target = CAGrad(zeta * (target + var * 2.0f) - result) + result;
После чего осуществляем обратный проход моделей и возвращаем Критика в режим обучения модели.
bTarget.AssignArray(target); if(!critic.backProp(GetPointer(bTarget), GetPointer(cActorExploer)) || !cActorExploer.backPropGradient(SecondInput, GetPointer(temp))) { critic.TrainMode(true); return false; } critic.TrainMode(true);
Далее нам остается обновить целевые модели. И здесь я внес очередные дополнения для предотвращения искажения оценок будущих состояний и адаптации моделей Критиков под значения их целевых копий.
Обновления параметров целевых моделей на каждой итерации осуществляется только при отказе от их использования для оценки последующего состояния. Если же целевые модели используются в процессе обучения, то их обновление осуществляется с задержкой.
Поэтому мы сначала проверяем необходимость обновления моделей и только потом осуществляем операции.
if(!!NextState) { if(iUpdateDelayCount > 0) { iUpdateDelayCount--; return true; } iUpdateDelayCount = iUpdateDelay; } if(!cTargetCritic1.WeightsUpdate(GetPointer(cCritic1), tau) || !cTargetCritic2.WeightsUpdate(GetPointer(cCritic2), tau) || !cTargetNu.WeightsUpdate(GetPointer(cNu), tau)) { PrintFormat("Error of update target models: %d", GetLastError()); return false; } //--- return true; }
После успешного завершения всех итераций метода мы завершаем его работы с результатом true.
Декомпозиция вознаграждений и использование векторов повлекло изменения и в других методах. В том числе и методах работы с файлами. Но мы не будем сейчас на них останавливаться. Вы можете самостоятельно ознакомиться с ними, как и с полным кодом всех методов нового класса, во вложенном файле "MQL5\Experts\SAC-D&DICE\Net_SAC_D_DICE.mqh".
2.2 Корректируем структуры хранения данных
А мы двигаемся дальше и переходим к работе над файлом "MQL5\Experts\SAC-D&DICE\Trajectory.mqh". Но если раньше мы изменяли здесь архитектуру моделей, то сейчас мы её оставили практически без изменений. Нам нужно лишь изменить количество нейронов на выходе Критика. Их должно быть достаточно для декомпозиции функции вознаграждения. Но прежде, чем указать их количество, давайте определим структуру декомпозированного вознаграждения.
В первом элементе с индексом "0" мы укажем относительное изменение баланса. Как вы знаете, основная наша цель максимизация прибыли на рынке.
В параметре с индексом "1" мы укажем относительную величину изменения Эквити. Отрицательное значение укажет на нежелательную просадку. А положительная на нереализованную прибыль.
Ещё один элемент выделим для штрафов за отсутствие открытых позиций.
Далее мы добавим логарифмы вероятностей действий. Как Вы знаете длина вектора логарифмов вероятностей равна вектору действий.
//+------------------------------------------------------------------+ //| Rewards structure | //| 0 - Delta Balance | //| 1 - Delta Equity ( "-" Drawdown / "+" Profit) | //| 2 - Penalty for no open positions | //| 3... - LogProbs vector | //+------------------------------------------------------------------+
Таким образом, размер нейронного слоя результатов Критика на 3 элемента больше количества действий.
#define NActions 6 //Number of possible Actions #define NRewards 3+NActions //Number of rewards
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } //--- Actor ........ ........ //--- Critic critic.Clear(); //--- Input layer ........ ........ //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Далее надо сказать, что декомпозиция вознаграждения изменила и структуру хранения данных в буфере воспроизведения опыта. Теперь нам недостаточно одной переменной для записи вознаграждения. Нужен массив данных. В то же время мы внесли энтропийную составляющую в массив вознаграждений и нам не нужен отдельный массив для повторной записи этих значений. Следовательно, в структуре описания состояния мы заменим массив log_prob на rewards. И скорректируем методы копирования структуры и работы с файлами.
struct SState { float state[HistoryBars * BarDescr]; float account[AccountDescr - 4]; float action[NActions]; float rewards[NRewards]; //--- SState(void); //--- bool Save(int file_handle); bool Load(int file_handle); //--- overloading void operator=(const SState &obj) { ArrayCopy(state, obj.state); ArrayCopy(account, obj.account); ArrayCopy(action, obj.action); ArrayCopy(rewards, obj.rewards); } };
В структуре траектории STrajectory мы удаляем массив вознаграждений Rewards, так как вознаграждение теперь будем расписывать в структуре состояния SState. И вносим точечные правки в методы структуры.
struct STrajectory { SState States[Buffer_Size]; int Total; float DiscountFactor; bool CumCounted; //--- STrajectory(void); //--- bool Add(SState &state); void CumRevards(void); //--- bool Save(int file_handle); bool Load(int file_handle); };
А с полным кодом упомянутых структур и их методов можно ознакомиться во вложении.
2.3 Создание советников обучения модели
Мы двигаемся дальше и переходим к работе над советниками обучения модели. В процессе обучения, как и ранее, мы используем 3 советника:
- Research — сбор базы примеров
- Study — обучение моделей
- Test — проверка полученных результатов.
В советниках Research и Test изменения коснулись лишь подготовки структуры описания состояния окружающей среды и полученного вознаграждения в завершении метода OnTick. Если раньше мы суммировали вознаграждения и штрафы, то сейчас мы каждый компонент вносим в свой элемент массива. При этом важно соблюдение указанной выше структуру данных. Каждый элемент массива должен быть заполнен в обязательном порядке. Если значение компоненты отсутствует, то записываем "0" в соответствующий элемент массива. Такой подход даст нам уверенность в корректности используемых данных.
void OnTick() { //--- ........ ........ //--- sState.rewards[0] = bAccount[0]; sState.rewards[1] = 1.0f-bAccount[1]; vector<float> log_prob; Actor.GetLogProbs(log_prob); if((buy_value + sell_value) == 0) sState.rewards[2] -= (float)(atr / PrevBalance); else sState.rewards[2] = 0; for(ulong i = 0; i < NActions; i++) { sState.action[i] = ActorResult[i]; sState.rewards[i + 3] = log_prob[i] * LogProbMultiplier; } if(!Base.Add(sState)) ExpertRemove(); }
С полным кодом советников можно ознакомиться во вложении.
Обучение моделей, как обычно, осуществляется в советнике Study. Как уже было сказано выше, процесс обучения моделей мы разбиваем на 2 этапа:
- Обучение с фактическим накопительным вознаграждением (без целевых моделей),
- Обучение с использованием целевых моделей.
Длительность первого этапа определяется константой.
#define StartTargetIteration 20000
Стоит обратить внимание, что обучение без использования целевых моделей осуществляется только при первом запуске советника Study, когда нет предварительно обученных моделей.
Если же при запуске советнику обучения удалось загрузить предварительно обученные модели, то в таком случае целевые модели используются с первой итерации обучения.
Данный контроль реализован в методе OnInit советника.
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; } //--- load models if(!Net.Load(FileName, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Net.Create(actor, critic, critic, critic, LatentLayer)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; StartTargetIter = StartTargetIteration; } else StartTargetIter = 0; //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Как можно заметить, при создании новых моделей в переменную StartTargetIter мы записываем значение константы StartTargetIteration. Если же загружены предварительно обученные модели, то в переменную задержки сохраняем "0".
Итерации обучения организованы в методе Train. В начале метода мы, как обычно, определяем количество сохраненных траекторий в буфере воспроизведения опыта. И организовываем цикл обучения с числом итераций, заданным во внешнем параметре советника.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = (int)((MathRand() / 32767.0) * (total_tr - 1)); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
В теле цикла мы случайным образом семплируем состояние в одной из сохраненных траекторий. После чего мы переносим информацию о выбранном состоянии в буфера данных и вектор.
//--- bState.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- bActions.AssignArray(Buffer[tr].States[i].action); vector<float> rewards; rewards.Assign(Buffer[tr].States[i].rewards);
Обратите внимание, что на данном этапе мы подготавливаем информацию только о выбранном состоянии. Чтобы не выполнять лишнюю работу, информацию о последующем состоянии мы будем формировать только в случае необходимости.
Мы проверяем необходимость использования целевых моделей для оценки последующего состояния путем сравнения текущей итерации обучения и значения переменной StartTargetIter. Если количество итераций не достигло порогового значения, то осуществляем обучения на кумулятивных значениях. Но здесь есть один момент. При сохранении данных в буфер воспроизведения опыта мы подсчитали накопительным итогом значения всех компонент вознаграждения. Только вот энтропийная составляющая нам необходима без накопительного итога. Поэтому, мы организовываем цикл и снимаем накопленные значения только с энтропийной составляющей функции вознаграждения.
//--- if(iter < StartTargetIter) { ulong start = rewards.Size() - bActions.Total(); for(ulong r = start; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, NULL, NULL, DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
И далее вызываем метод обучения нашего нового класса. Здесь мы указываем "NULL" в параметрах последующего состояния.
После достижения порогового значения использования целевых функций мы сначала подготовим информацию о последующем состоянии системы.
else { //--- Target bNextState.AssignArray(Buffer[tr].States[i + 1].state); PrevBalance = Buffer[tr].States[i].account[0]; PrevEquity = Buffer[tr].States[i].account[1]; if(PrevBalance == 0) { iter--; continue; } bNextAccount.Clear(); bNextAccount.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); bNextAccount.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); bNextAccount.Add(Buffer[tr].States[i + 1].account[2]); bNextAccount.Add(Buffer[tr].States[i + 1].account[3]); bNextAccount.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); bNextAccount.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance); x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); bNextAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); bNextAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Затем мы снимаем накопительные значения по всем компонентам функции вознаграждения, оставляя лишь вознаграждения текущего состояния.
for(ulong r = 0; r < rewards.Size(); r++) rewards[r] -= Buffer[tr].States[i + 1].rewards[r] * DiscFactor; if(!Net.Study(GetPointer(bState), GetPointer(bAccount), GetPointer(bActions), rewards, GetPointer(bNextState), GetPointer(bNextAccount), DiscFactor, Tau)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
И вызываем метод обучения модели нашего класса. На этот раз мы указываем объекты с данными последующего состояния.
В завершении итерации цикла мы выводим сообщение для информирования пользователя и переходим к следующей итерации.
//--- if(GetTickCount() - ticks > 500) { float loss1, loss2; Net.GetLoss(loss1, loss2); string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), loss1); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), loss2); Comment(str); ticks = GetTickCount(); } }
После успешного завершения всех итераций цикла мы очищаем поле комментариев на графике. Осуществляем принудительное обновление целевых моделей. Выводим результат обучения в журнал MetaTrader 5 и инициализируем процесс завершения работы советника.
Comment(""); //--- float loss1, loss2; Net.GetLoss(loss1, loss2); Net.TargetsUpdate(Tau); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", loss1); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", loss2); ExpertRemove(); //--- }
На этом мы завершаем работу с советниками обучения модели. С полным кодом всех программ, используемых в статье, Вы можете ознакомиться во вложении.
3. Тестирование
Выше был предложен вариант реализации подхода декомпозиции функции вознаграждения на базе алгоритма SAC+DICE и теперь мы можем на практике оценить результаты проделанной работы. Как и ранее обучение моделей осуществлялось на исторических данных инструмента EURUSD тайм-фрейм H1 временной интервал в первые 5 месяцев 2023 года. Все параметры индикаторов используются по умолчанию. Начальный баланс 10000 USD.
Процесс обучения модели итерационный, чередующийся этапами сбора примеров в буфер накопления опыта и обновления параметров модели.
На первом этапе мы создаем первичную базу примеров с использованием моделей Актеров, заполненных случайными параметрами. В результате чего мы получаем ряд случайных проходов, которые генерируют несвязанные политикой наборы данных "Состояние → Действие → Новое состояние → Вознаграждение".
В отличие от всех ранее рассмотренных алгоритмов, в данном случаем мы собираем декомпозированные данные о вознаграждении от окружающей среды за совершаемые действия Агента.
После сбора примеров мы осуществляем первичное обучение нашей модели. Для этого мы запускаем советник "..\SAC-D&DICE\Study.mq5".
Должен сказать, что при первичном обучении без использования целевых моделей мы наблюдаем устойчивую тенденцию к снижению ошибки обоих Критиков. Однако, при использовании целевых моделей для оценки последующего состояния наблюдаются хаотичные (не частые) всплески ошибки прогнозирования. После которых можно наблюдать плавный возврат к предыдущему уровню ошибки.
На втором этапе мы повторно запускаем советник сбора обучающих данных в режиме оптимизации тестера стратегий с полным перебором параметров. На этот раз при всех прохода мы используем обученного на первом этапе оптимистичного Актера. Разброс результатов отдельных проходов ниже первичного сбора данных и обусловлен стохастичностью политики Актера.
Процесс сбора примеров и обучения модели повторяем несколько раз до получения желаемого результата или достижения локального минимума, когда очередная итераций сбора примеров и обучения модели не дает прогресса результатов.
В процессе обучения модели мы получили политику Актера, способную генерировать небольшую прибыль за обучающий период.
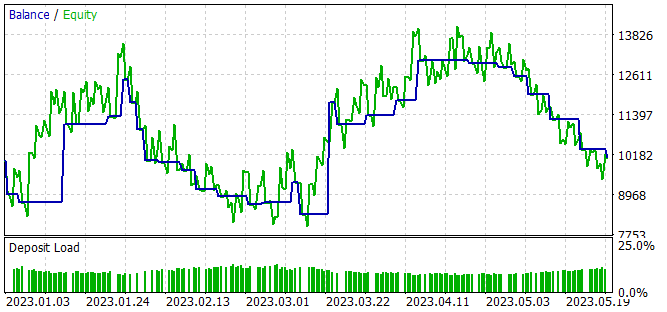
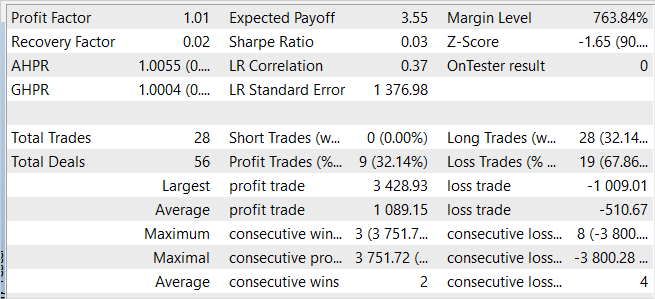
Несмотря на полученную прибыль, выученная политика далека от наших желаний. На графике баланса мы видим волнообразное движение с довольно большой амплитудой. Из 28 сделок только 32% было закрыто с прибылью. Общая прибыль была достигнута благодаря превышению размера прибыльной сделки над убыточной. Так средняя прибыль по сделке в 2 раза превышает средний убыток. А максимальная прибыль на одну сделку почти в 3.5 раза превышает максимальный убыток. В результате профит фактор чуть выше 1.
В защиту модели можно сказать, что на новых данных советник также продемонстрировал прибыль. За один месяц после периода обучения модель смогла получить почти 20% дохода, что выше результата на обучающей выборке. Однако статистика результатов сопоставима с данными на обучающей выборке. В процессе тестирования было совершено всего 4 сделки и только одна из них закрыта с прибылью. Но прибыль по этой сделке в 12.8 раз превышает максимальную из убыточных сделок.
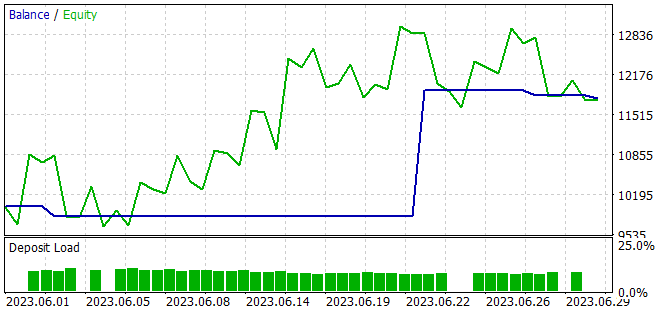
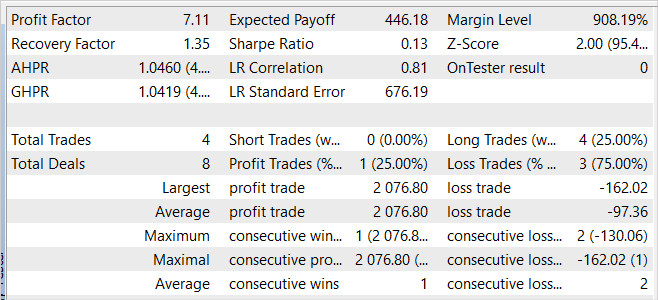
Сопоставляя вместе результаты на обучающей выборке и за последующий период, можно предположить, что на новых данных мы наблюдаем начало волны доходности. За которой в обозримом будущем возможен спад.
В целом модель способна генерировать прибыль, но требуется дополнительная оптимизация.
Заключение
В данной статье мы познакомились с подходом декомпозиции функции вознаграждения, который позволяет более эффективно обучать Агентов. Декомпозиция вознаграждения позволяет анализировать влияние различных компонентов на принимаемые Агентом решения.
Мы реализовали алгоритм средствами MQL5 и интегрировали декомпозицию функции вознаграждения в метод SAC+DICE.
В процессе практического тестирования реализованного алгоритма нам удалось получить модель, способную генерировать прибыль как на обучающей выборке, так и вне ее. Что свидетельствуют об обобщающей способности алгоритма.
Однако, полученные результаты далеки от наших желаний. В то же время декомпозиция функции вознаграждения позволяет проанализировать влияние отдельных компонентов функции вознаграждения на результат обучения. Я предлагаю Вам поэкспериментировать с включением и исключением отдельных компонентов. И оценить их влияние на результат обучения.
Ссылки
- Conflict-Averse Gradient Descent for Multi-task Learning
- Value Function Decomposition for Iterative Design of Reinforcement Learning Agents
- Нейросети — это просто (Часть 52): Исследование с оптимизмом и коррекцией распределения
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | Study.mq5 | Советник | Советник обучения агента |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 5 | Net_SAC_D_DICE.mqh | Библиотека класса | Класс модели |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования