busca de padrões, descrevendo os principais padrões
Todas as suposições básicas da teoria de correlação e regressão são baseadas na suposição de que os dados em estudo são normalmente distribuídos. Seus insumos (preço) têm uma distribuição normal?
Todas as suposições básicas da teoria de correlação e regressão são baseadas na suposição de que os dados em estudo são normalmente distribuídos. Seus insumos (preço) têm uma distribuição normal?
não o conseguiu
Em princípio, mostrarei que o RMS detecta qualquer padrão embutido em uma série de dígitos, incluindo séries temporais (RT), creio, independentemente da natureza da aparência desses dígitos na série. Todas estas e outras sutilezas serão discutidas usando exemplos concretos, incluindo a análise de séries aleatórias.
RMS encontrará um padrão válido ou fictício, mas devido à falta de normalidade de distribuição, o valor preditivo do modelo será 0. Estas não são sutilezas, esta é a base.
O que, exatamente, você não entendeu?
RMS encontrará um padrão real ou imaginário, mas devido à falta de normalidade da distribuição, o valor preditivo do modelo será 0. Isto não é sutileza, é a base.
A RMS encontrará a dependência mais adequada, ao invés de uma dependência derivada. E sobre a ausência ou presença de normalidade na distribuição dos dados iniciais, vamos abrir uma discussão separada e deixar que os especialistas desta base falem aqui em paralelo.
Recebi..... E certo - esqueça, normalidade! Só atrapalha.
P.S. o valor preditivo do modelo será próximo de 0
Vamos começar com uma função linear.
Imaginemos que a série é dada pelos números Yi = a+bxi:
xi Yi
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
Aqui está um gráfico dos valores reais e calculados, o erro do modelo é 2,78163E-14%:
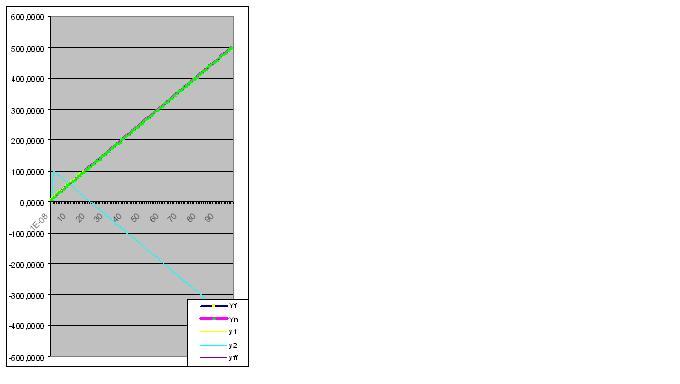
Recebi..... E com razão - que se lixe, a normalidade! Só atrapalha.
P.S. o valor preditivo do modelo será próximo de 0
Devido a sua persistência, tenho que começar por demonstrar a capacidade de previsão do modelo, analisando a função Y=tg(0,1x)+2 e introduzindo os primeiros 8 pares de dígitos:
xi Yi
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
Erro 0,427140953%:
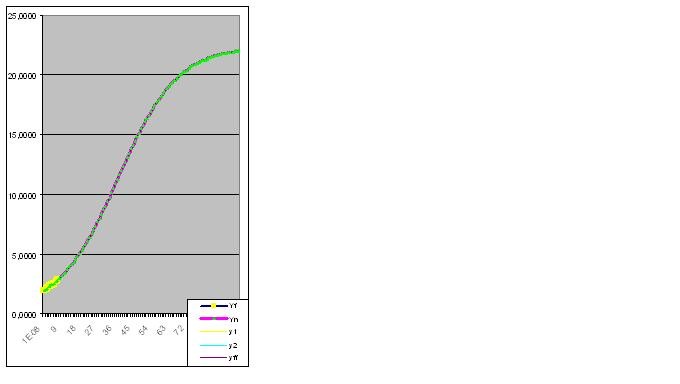
Entretanto, uma vez introduzido o 9º par de dígitos, o modelo prevê imediatamente sobre o comportamento "estranho" do objeto no futuro:
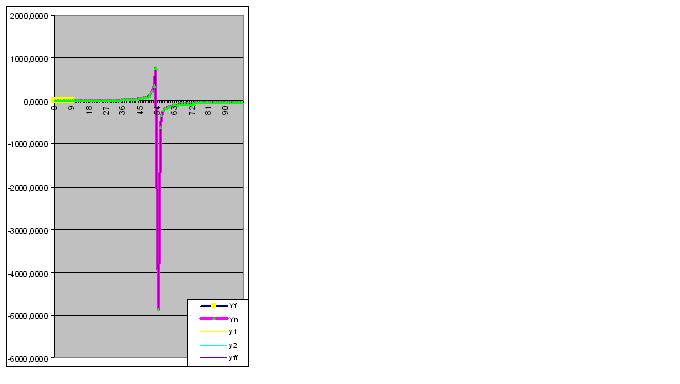
A entrada de mais dados aproxima a "anomalia" prevista dos dados originais:
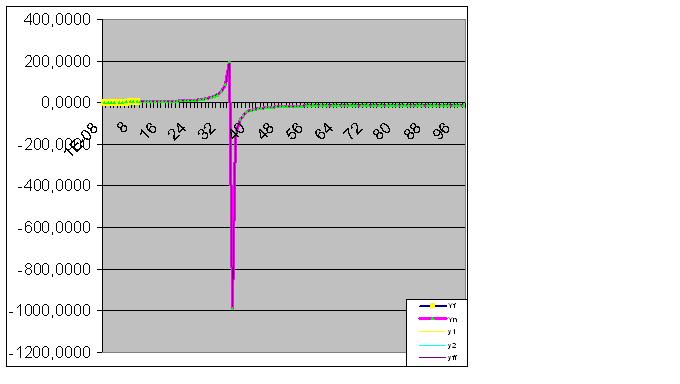
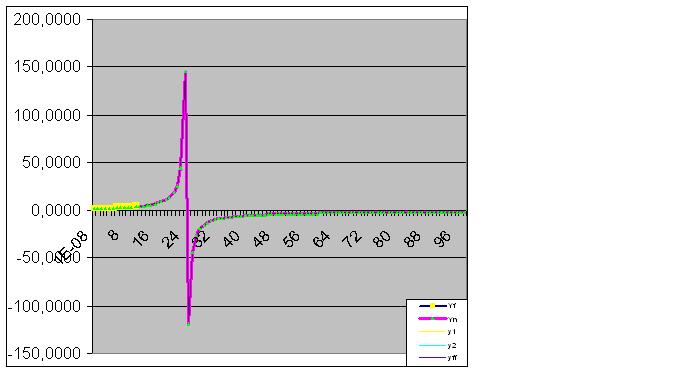
Aqui os dados brutos também começaram a realizar a "simulação" prevista:
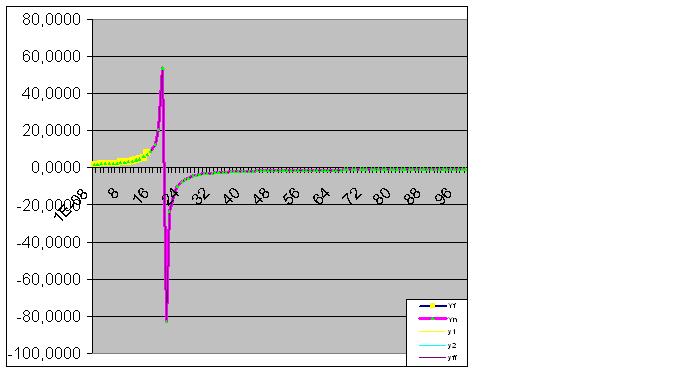
Finalmente, a previsão é perfeitamente cumprida:
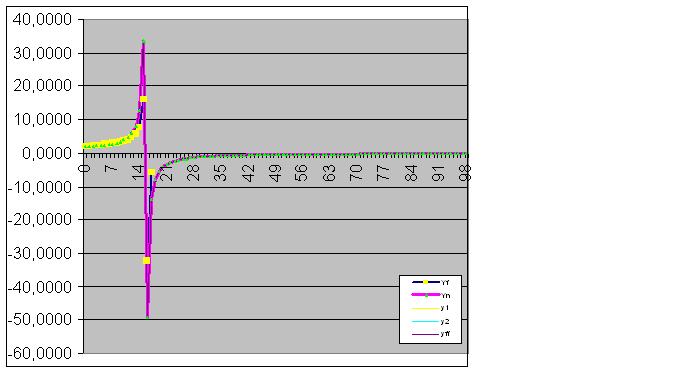
Em seguida, o modelo captura perfeitamente o estado final do objeto, de modo que a soma dos valores reais da função seja igual ao RMS calculado com a precisão do computador
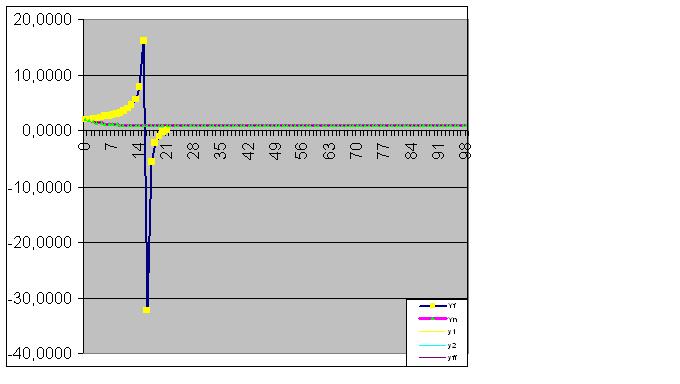
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Caros membros do fórum, não é segredo que a questão de encontrar as dependências que descrevem os padrões básicos do mercado é uma questão importante. Aqui tentaremos abordar esta questão por todos os meios de análise disponíveis, incluindo várias propostas dos participantes sobre este assunto e o material teórico e prático acumulado até este momento de todas as fontes possíveis. Como resultado deste trabalho, se nos debruçarmos apenas sobre uma visão desta função, penso que consideraremos que o tempo e o esforço não foram despendidos em vão.
Começarei por demonstrar as capacidades do RMS com exemplos simples de descrições de padrões bem conhecidos: linear, parábola, hipérbole, expoente, seno, cosseno, tangente, cotangente e outros, bem como sua combinação, que certamente estão presentes no mercado. Por favor, apoiem-me neste impulso com sugestões construtivas e críticas saudáveis, se necessário.