[Arquivo!] Pura matemática, física, química, etc.: problemas de treinamento do cérebro não relacionados ao comércio de qualquer forma - página 614

Novo comentário
 
Mathemat:

Dima, por que você quer saber a probabilidade que difere de um por milésimos de um por cento? Se você quer garantias, não há nenhuma. Os ganhadores do Prêmio Nobel (LTCM) e o próprio Niederhoffer se esconderam atrás de probabilidades em algum grau menos uma - e ainda "acertaram".

Por milésimos de por cento - não é necessário. Mas 120 transações é muito, deve ser possível calcular para um pequeno número de transações, por exemplo - para 20, 30, 40. E 30% não é suficiente para 120.

E probabilidades muito pequenas (muito grandes) são usadas para calcular a vida útil aproximada do sistema. É importante saber quanto tempo vai durar - um ano ou 10 anos.
Há algo em que se possa confiar? A matemática é o melhor caminho a seguir.
 
Bem, pelo menos leia em algum terw básico, ele virá a calhar de qualquer maneira.
 
GaryKa, Mathemat

Certo?



 
DmitriyN: Certo?

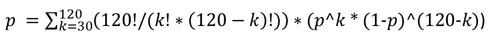
Isso mesmo!

Mas os erros de arredondamento podem consumir toda a precisão. É melhor contar a soma de 0 a 30. Será igual à adição da probabilidade que você quer saber.

 
Se as bolas forem devolvidas, então sempre p=q, para que possamos simplificar a fórmula no lado direito (* p^120)
 
Mislaid: Resolvemos o problema cardinalmente: sem igualdade. Determinar que os conjuntos de números nas faces do cubo não devem se sobrepor.

Há casos, há casos em que a soma dos rostos é igual a 17.

Por exemplo, (333332) > (662111), com uma probabilidade de vitória de 23/36 ~ 0,64. É verdade, não é simples: (662111) não ganha por nenhuma margem apreciável.

Parece que até agora a soma dos rostos de 18 é a mais fértil.

 
GaryKa:
Se devolvermos as bolas, então é sempre p=q, para que possamos simplificar a fórmula no lado direito (* p^120)

Não importa realmente se voltamos ou não. Extraímos muito pouco para fazer alguma diferença. Mas pode ser simplificada decentemente. E entre parênteses com potências, o multiplicador (1/2)^120 permanecerá.

Hehe.

2 Dima: Não se preocupe com estas combinações. Controle a distribuição normal e leve uma integral definida de zero até o limite inferior correspondente aos seus 30 anos. Você cometerá um grande erro com combinações nesta fórmula, a menos que encontre uma fórmula analítica para a simples soma de combinações.

Ou tente a soma das combinações de 0 a 30, as notas p não o incomodarão. Você pode ter sorte.

P.S. Em resumo, é fácil. Veja aqui.

Você precisa calcular k1, k2 e depois a integral.

Tome k1=0, k2=30, isto é mais preciso. n=120, p=q=1/2. Depois

(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477

(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10,954.

Também 1/sqrt(2*pi) ~ 0,39894 vem a calhar.

Substituir os dois primeiros números nos limites de integração, e substituir 0,39894*exp(-x^2/2) na função integrand, e obtemos (aqui está um serviço ao tomar certos integrais):

2.163*10^(-8).

Portanto, sua probabilidade é de 1-2,163*10^(-8) ~ 0,99999998.

Não tente sequer assumir a inicial da função sob a integral: ela é não-inteira.

 
Mathemat: ... Trabalhar a distribuição normal ... a menos que você possa encontrar uma fórmula analítica para uma simples soma de combinações ...
Estas suas palavras me deram uma idéia interessante para tentar encontrar uma fórmula analítica para calcular uma combinação através de uma distribuição normal ))
 
Mathemat:
Vou tentar descobrir. Bons links.
 
GaryKa: Estas suas palavras me deram uma idéia interessante - tentar encontrar uma fórmula analítica para calcular a combinação através de uma distribuição normal ))
Este é o teorema local de Moab-Laplace.
1...607608609610611612613614615616617618619620621...628
Novo comentário