
Redes neurais em trading: Modelos de espaço de estados
Introdução
Recentemente, tornou-se amplamente difundida a adaptação de grandes modelos previamente treinados em grandes conjuntos de dados brutos de diversas áreas, como texto, imagens, áudio, séries temporais, entre outros, para novas tarefas.
Embora esse conceito não dependa de uma arquitetura específica, a maioria dos modelos é baseada em um único tipo de arquitetura: Transformer e sua camada principal, Self-Attention. A eficiência do Self-Attention deve-se à sua capacidade de direcionar informações de forma densa para a janela de contexto, o que permite modelar dados complexos. No entanto, essa característica apresenta desvantagens fundamentais: a incapacidade de modelar qualquer coisa além da janela final e o escalonamento quadrático em relação ao comprimento da janela.
Nas tarefas de modelagem de sequências, uma solução alternativa pode ser o uso de modelos estruturados de sequências em espaço de estados (Space Sequence Models — SSM). Esses modelos podem ser interpretados como uma combinação de redes neurais recorrentes (RNN) e redes neurais convolucionais (CNN). Esta classe de modelos pode ser computada de maneira muito eficiente, com escalonamento linear ou quase linear em relação ao comprimento da sequência. Além disso, possui mecanismos fundamentais para modelar dependências de longo alcance em determinadas modalidades de dados.
Um dos algoritmos propostos no artigo "Mamba: Linear-Time Sequence Modeling with Selective State Spaces" permite o uso de modelos de espaço de estados para a previsão de séries temporais. Ele apresenta uma nova classe de modelos de espaço de estados seletivos.
Os autores do artigo definem a principal limitação dos modelos existentes: a capacidade de selecionar informações de maneira eficiente a partir dos dados brutos (ou seja, focar em determinados dados ou ignorá-los). Eles desenvolvem um mecanismo simples de seleção, no qual os parâmetros do SSM dependem dos dados brutos. Isso permite que o modelo filtre informações irrelevantes e retenha informações relevantes por tempo indeterminado.
Os autores do método simplificam as arquiteturas anteriores de modelos profundos de sequência, combinando o design das arquiteturas SSM com o design MLP em um único bloco, resultando em uma arquitetura simples e uniforme (Mamba), que incorpora espaços de estados seletivos.
Os SSM seletivos e, consequentemente, a arquitetura Mamba são modelos totalmente recorrentes com propriedades-chave que os tornam adequados como base para modelos gerais que trabalham com sequências.
- Alta qualidade: a seletividade garante um desempenho elevado em modalidades densas.
- Treinamento e inferência rápidos: os cálculos e o uso de memória são escalonados de forma linear em relação ao comprimento da sequência durante o treinamento, enquanto o desdobramento autorregressivo do modelo durante a inferência requer apenas tempo constante por etapa, já que não exige o armazenamento em cache de elementos anteriores.
- Contexto de longo prazo: a combinação de qualidade e eficiência proporciona um aumento no desempenho ao lidar com sequências de grande dimensão.
1. O algoritmo Mamba
Os autores do método Mamba argumentam que o problema fundamental da modelagem de sequências é a perda de contexto em um estado mais reduzido. A partir dessa perspectiva, é possível analisar os compromissos dos modelos sequenciais populares. Por exemplo, a atenção (attention) é simultaneamente eficiente e ineficiente, pois não comprime explicitamente o contexto de forma alguma. Isso é evidente pelo fato de que a inferência autorregressiva exige o armazenamento explícito de todo o contexto (ou seja, o cache de Key-Value), resultando diretamente em uma inferência lenta com tempo linear e treinamento do Transformer em tempo quadrático.
Por outro lado, os modelos recorrentes são eficientes porque possuem um estado finito, o que implica inferência em tempo constante e treinamento em tempo linear. No entanto, sua eficácia é limitada pela capacidade de comprimir o contexto.
Para entender esse princípio, os autores do método destacam, em seu trabalho, a solução de duas tarefas sintéticas:
- A tarefa de Cópia Seletiva. Ela exige raciocínio baseado no conteúdo para que seja possível memorizar tokens relevantes e filtrar os irrelevantes.
- A tarefa de Cabeças de Indução. Esse mecanismo explica a maior parte das habilidades dos LLM em aprendizado contextual. Resolver essa tarefa requer raciocínio dependente do contexto para saber quando obter a conclusão correta no contexto apropriado.
Essas tarefas revelam os modos de falha dos modelos LTI. Sob a perspectiva recorrente, sua dinâmica constante não permite selecionar as informações corretas de seu contexto ou influenciar o estado oculto transmitido ao longo da sequência de maneira independente dos dados brutos. Sob a perspectiva da convolução, sabe-se que convoluções globais podem resolver a tarefa básica de cópia, pois ela requer apenas a percepção do tempo. No entanto, enfrentam dificuldades na tarefa de cópia seletiva devido à falta de percepção do conteúdo. Mais especificamente, a distância entre os dados brutos e os resultados varia e não pode ser modelada por kernels de convolução estática.
Portanto, o compromisso de eficiência em modelos sequenciais é caracterizado pela qualidade com que eles comprimem seu estado. Nesse sentido, os autores do método sugerem que o princípio fundamental para a construção de modelos sequenciais é a seletividade, ou seja, a capacidade de focar nos dados brutos ou filtrá-los no estado sequencial, de acordo com o contexto. Em particular, o mecanismo de seleção controla como as informações são propagadas ou interagem nas dimensões da sequência.
Uma maneira de incorporar o mecanismo de seleção nos modelos é permitir que seus parâmetros, que afetam a interação ao longo da sequência, dependam dos dados brutos. A principal diferença é fazer com que alguns parâmetros, como Δ B e C, sejam funções dos dados brutos, além de implementar alterações associadas às formas dos tensores. Especificamente, esses parâmetros agora possuem uma dimensão equivalente ao comprimento L, o que significa que o modelo deixou de ser invariante no tempo para se tornar dependente do tempo.
Os autores do método escolhem especificamente:
- SB(x) = LinearN(x)
- SC(x) = LinearN(x)
- SΔ(x) = BroadcastD(Linear1(x))
- τΔ = SoftPlus
A escolha de SΔ e τΔ decorre da conexão com os mecanismos de portas das RNNs.
Os autores do método buscam tornar os SSM eficientes e seletivos no hardware moderno (GPU). Em um nível elevado, modelos recorrentes como SSM sempre equilibram eficiência e velocidade: modelos com maior dimensionalidade do estado oculto devem ser mais eficazes, mas mais lentos. Assim, o desafio enfrentado pelos autores do método Mamba foi maximizar a dimensionalidade do estado oculto sem comprometer a velocidade do modelo ou aumentar o consumo de memória.
O mecanismo de seleção visa superar as limitações dos modelos LTI. No entanto, é necessário retomar a questão do cálculo dos SSM. Para resolver essa questão, os autores do método utilizam três métodos clássicos: fusão de kernels, varredura paralela e recomputação. Eles fazem duas observações principais:
- Os cálculos recorrentes ingênuos utilizam O(BLDN) FLOP, enquanto os cálculos convolucionais usam O(BLD log(L)) FLOP. O primeiro apresenta um coeficiente constante menor. Assim, para sequências longas e dimensões de estado N não muito grandes, o modo recorrente pode, na verdade, utilizar menos FLOP.
- Duas questões principais envolvem o caráter sequencial da repetição e o grande uso de memória. Para abordar o último problema, assim como no modo convolucional, podemos tentar não calcular o estado completo h.
A ideia central é aproveitar as propriedades dos aceleradores modernos (GPU) para calcular o estado h apenas nos níveis mais eficientes da hierarquia de memória. Em particular, a largura de banda da memória limita a maioria das operações, e isso também se aplica à operação de varredura. Os autores do método utilizam a fusão de kernels para reduzir o número de operações de entrada e saída na memória, o que resulta em uma aceleração significativa em comparação com a implementação padrão.
Além disso, os autores do método aplicam cuidadosamente uma técnica clássica de recomputação para reduzir a demanda de memória: os estados intermediários não são armazenados, mas recalculados no sentido inverso durante o carregamento dos dados brutos.
Os SSM seletivos são transformações de sequência autônomas que podem ser integradas de forma flexível em redes neurais.
O mecanismo de seleção é um conceito mais amplo que pode ser aplicado de maneiras diversas a outros parâmetros ou por meio de diferentes transformações.
A seletividade permite filtrar tokens irrelevantes ou ruidosos que podem surgir entre os dados brutos de interesse. Um exemplo disso é a tarefa de cópia seletiva, mas esse fenômeno é amplamente encontrado em modalidades de dados comuns, especialmente em dados discretos. Esse atributo decorre da capacidade do modelo de filtrar mecanicamente quaisquer dados brutos específicos Xt.
Empiricamente, observou-se que muitas modelos sequenciais não melhoram com contextos mais longos, apesar do princípio de que mais contexto deveria resultar em um desempenho estritamente melhor. Isso se deve ao fato de que muitos modelos sequenciais não conseguem ignorar de forma eficaz contextos irrelevantes quando necessário.
Por outro lado, modelos seletivos podem simplesmente redefinir seu estado a qualquer momento para eliminar histórico indesejado, melhorando, em princípio, seu desempenho de forma monótona com o aumento do comprimento do contexto.
Abaixo, é apresentada a visualização do método criada pelos autores.
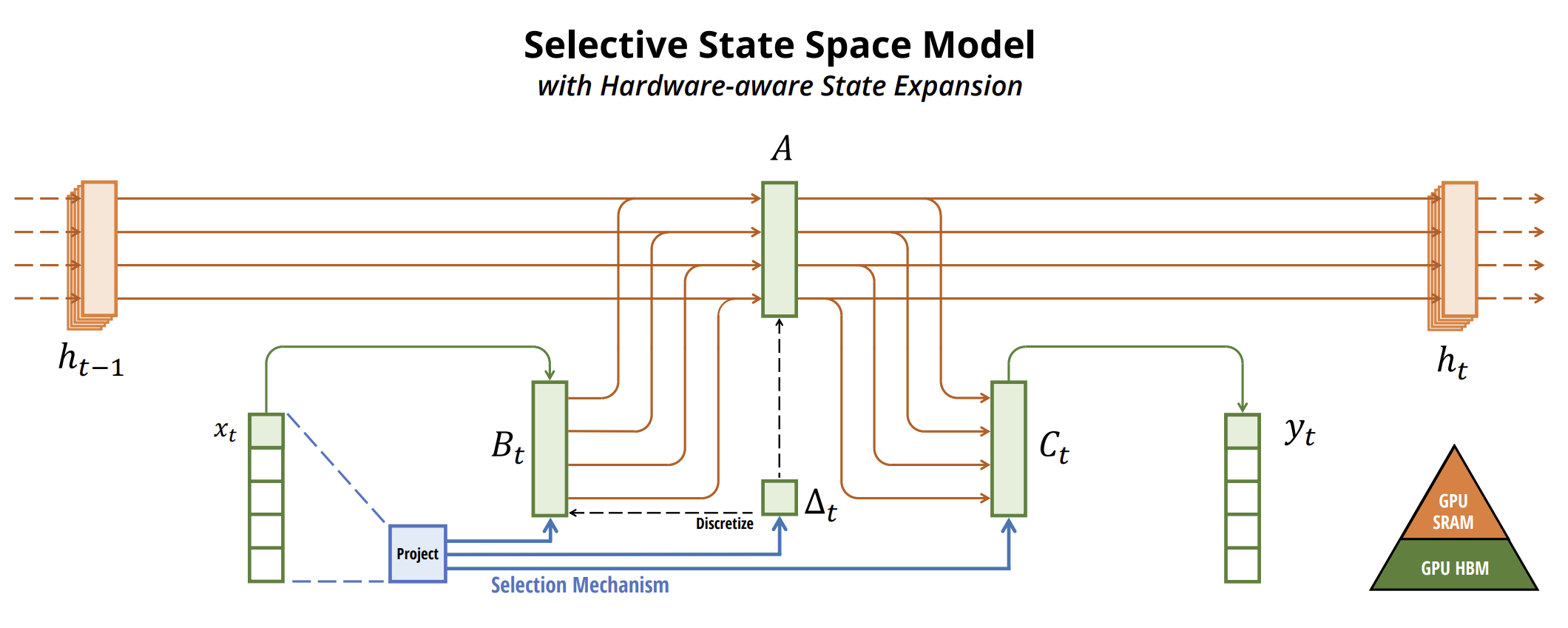
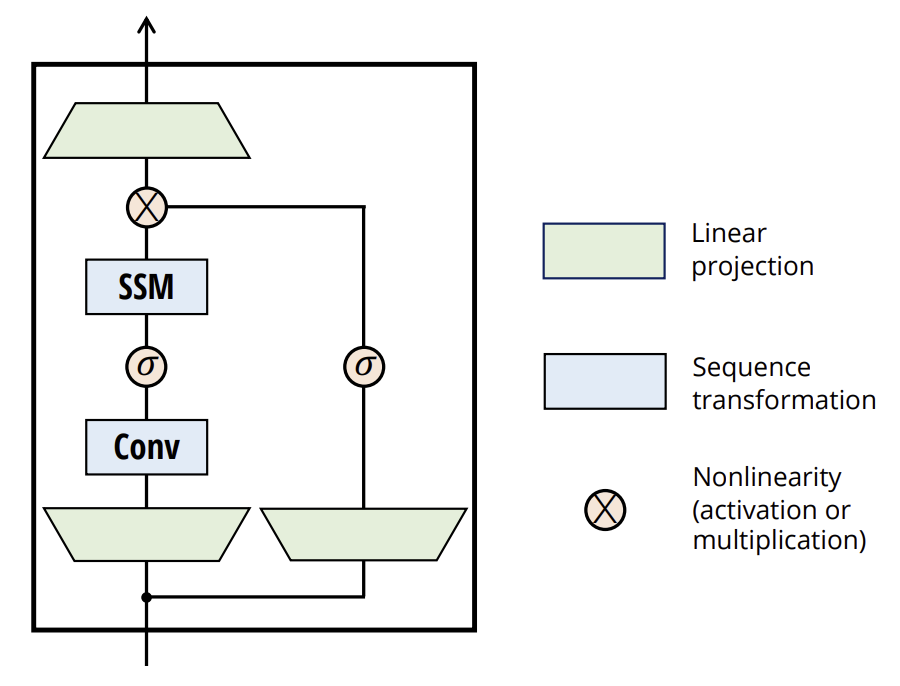
2. Implementação em MQL5
Após explorar os aspectos teóricos do método Mamba, passamos à implementação prática dos enfoques propostos utilizando MQL5. Dividiremos o trabalho em duas etapas. Primeiramente, construiremos uma classe para implementar o algoritmo SSM, que constitui um dos componentes internos do método Mamba. Em seguida, estruturaremos os processos do algoritmo de nível superior.
2.1 Implementação do SSM
É importante observar que existem diversos algoritmos para a construção de SSM. Neste experimento, adotei uma abordagem um pouco distinta da implementação apresentada pelos autores do método Mamba, construindo um dos modelos mais simples de seleção de espaço de estados. Esse modelo foi implementado na classe CNeuronSSMOCL. Como objeto base, utilizamos a classe fundamental de camada neural totalmente conectada CNeuronBaseOCL. A estrutura da nova classe é apresentada abaixo.
class CNeuronSSMOCL : public CNeuronBaseOCL { protected: uint iWindowHidden; CNeuronBaseOCL cHiddenStates; CNeuronConvOCL cA; CNeuronConvOCL cB; CNeuronBaseOCL cAB; CNeuronConvOCL cC; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronSSMOCL(void) {}; ~CNeuronSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Na estrutura apresentada, podemos observar a declaração de uma constante, que define a dimensão do estado oculto de um único elemento (iWindowHidden), e cinco camadas neurais internas, cujas funcionalidades exploraremos no decorrer da implementação.
O conjunto de métodos que podem ser redefinidos em nossa classe é bastante comum. Imagino que você já tenha deduzido suas finalidades funcionais.
Todos os objetos internos da classe foram declarados como estáticos, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos declarados e herdados, como de costume, é realizada no método Init. Neste método, recebemos constantes que nos permitem determinar de forma inequívoca qual objeto o usuário deseja criar.
bool CNeuronSSMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Esses parâmetros são três:
- window: define o tamanho do vetor de um único elemento da sequência;
- window_key: especifica o tamanho do vetor da representação interna de um único elemento da sequência;
- units_count: indica o tamanho da sequência a ser analisada.
Conforme mencionado, neste experimento utilizamos um algoritmo SSM simplificado. Em particular, ele não implementa a separação de sequências multimodais em canais independentes.
No corpo do método, chamamos diretamente um método homônimo da classe base, onde a inicialização dos objetos e variáveis herdados já está implementada. Além disso, esse método realiza o controle mínimo necessário sobre os parâmetros recebidos do programa externo.
Após a execução bem-sucedida do método da classe base, avançamos para a inicialização dos objetos declarados nesta classe. Primeiro, inicializamos a camada interna de armazenamento do estado oculto.
if(!cHiddenStates.Init(0, 0, OpenCL, window_key * units_count, optimization, iBatch)) return false; cHiddenStates.SetActivationFunction(None); iWindowHidden = window_key;
Imediatamente, armazenamos o tamanho do vetor correspondente ao estado interno de um único elemento da sequência em uma variável local.
Observe que salvamos o valor do parâmetro diretamente, sem verificar sua validade. O ponto-chave é que, previamente, inicializamos conscientemente o objeto da camada interna, cujo tamanho é definido por esse parâmetro. Se o usuário fornecer um valor incorreto, serão gerados erros na etapa de inicialização da classe. Assim, a inicialização antecipada da camada interna realiza a verificação dos parâmetros de maneira indireta. Dessa forma, evitamos realizar operações desnecessárias nesta etapa.
É importante mencionar que o objeto cHiddenStates é usado apenas para armazenamento temporário de dados e sua função de ativação foi desativada intencionalmente.
Em seguida, inicializamos duas camadas de projeção de dados, que controlam a influência dos dados no resultado. A primeira camada inicializada é a de projeção do estado oculto.
if(!cA.Init(0, 1, OpenCL, iWindowHidden, iWindowHidden, iWindowHidden, units_count, 1, optimization, iBatch)) return false; cA.SetActivationFunction(SIGMOID);
Aqui utilizamos uma camada convolucional que nos permite criar projeções independentes do estado oculto de cada elemento da sequência. Para regular a influência de cada elemento no resultado, utilizamos a função sigmoide como função de ativação desta camada. Como você sabe, o intervalo de valores desta função é [0, 1]. Quando o valor é "0", o elemento não influencia o resultado geral.
Da mesma forma, inicializamos a camada de projeção dos dados brutos.
if(!cB.Init(0, 2, OpenCL, window, window, iWindowHidden, units_count, 1, optimization, iBatch)) return false; cB.SetActivationFunction(SIGMOID);
Observe que ambas as camadas de projeção retornam um tensor do tamanho do estado oculto, embora recebam tensores de tamanhos diferentes como entrada. Isso pode ser notado pelo tamanho da janela de dados analisada e pelo seu passo ao inicializar os objetos.
Para determinar a influência conjunta dos dados brutos e do estado oculto no resultado, planejamos usar uma soma ponderada. Para reduzir o número de operações realizadas, decidimos combinar este processo com a projeção dos dados para a dimensionalidade desejada dos resultados. Portanto, primeiro concatenamos os dados em um tensor unificado ao longo da dimensão dos elementos da sequência.
if(!cAB.Init(0, 3, OpenCL, 2 * iWindowHidden * units_count, optimization, iBatch)) return false; cAB.SetActivationFunction(None);
Depois disso, utilizamos mais uma camada convolucional interna.
if(!cC.Init(0, 4, OpenCL, 2*iWindowHidden, 2*iWindowHidden, window, units_count, 1, optimization, iBatch)) return false; cC.SetActivationFunction(None);
Por fim, no método de inicialização, substituímos os ponteiros dos buffers de resultados e gradientes de erro da nossa classe pelos buffers equivalentes da camada interna de projeção de resultados. Esse passo simples nos permite eliminar operações desnecessárias de cópia de dados durante a propagação para frente e reversa.
SetActivationFunction(None); if(!SetOutput(cC.getOutput()) || !SetGradient(cC.getGradient())) return false; //--- return true; }
E, claro, não esquecemos de monitorar o processo de execução das operações. No final do método, retornamos um valor lógico que indica o sucesso das operações para o programa chamador.
Após a conclusão do processo de inicialização da classe, avançamos para a construção dos algoritmos de propagação para frente. Como você sabe, essa funcionalidade é implementada no método redefinível feedForward. Aqui tudo é bastante simples e direto.
bool CNeuronSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cA.FeedForward(cHiddenStates.AsObject())) return false; if(!cB.FeedForward(NeuronOCL)) return false;
Nos parâmetros do método, recebemos um ponteiro para o objeto da camada neural anterior, que nos fornece os dados brutos.
No corpo do método, realizamos diretamente duas projeções (dos dados brutos e do estado oculto) para um formato compatível. Para isso, utilizamos os métodos de propagação para frente das respectivas camadas convolucionais internas.
As projeções obtidas são concatenadas em um único tensor ao longo da dimensão dos elementos da sequência.
if(!Concat(cA.getOutput(), cB.getOutput(), cAB.getOutput(), iWindowHidden, iWindowHidden, cA.Neurons() / iWindowHidden)) return false;
Por fim, no método, realizamos a projeção da camada concatenada para a dimensionalidade desejada dos resultados.
if(!cC.FeedForward(cAB.AsObject())) return false;
Aqui, é importante observar dois pontos. Aqui, é importante observar dois pontos. Primeiro, não transmitimos o resultado obtido para o buffer de resultados da camada atual — essa operação foi eliminada com a substituição dos ponteiros dos buffers de dados.
Em segundo lugar, você provavelmente notou que não atualizamos o estado oculto. Nesse formato, o método de propagação para frente parece incompleto. No entanto, o problema é que os dados atuais do estado oculto ainda são necessários para os cálculos da propagação reversa. Nesse caso, faz sentido atualizar o estado oculto durante o processo de propagação reversa, pois ele é utilizado apenas no algoritmo da camada atual.
Por outro lado, há uma desvantagem: durante a execução do modelo, não utilizamos os métodos de propagação reversa. Se transferirmos a atualização do estado oculto para esses métodos, ele simplesmente não será atualizado durante a execução do modelo, o que comprometerá todo o algoritmo.
Portanto, primeiro verificamos o modo de operação atual do modelo e, apenas no caso de execução do modelo, atualizamos o estado oculto. Para isso, somamos e normalizamos as projeções do estado oculto anterior e dos dados brutos.
if(!bTrain) if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true)) return false; //--- return true; }
Agora, nosso método de propagação para frente está completo. Retornamos para o programa chamador um valor lógico indicando o sucesso das operações realizadas.
Após a execução do algoritmo de propagação para frente, passamos a trabalhar nos métodos de propagação reversa. Como de costume, redefinimos dois métodos:
- calcInputGradients — distribuição dos gradientes de erro;
- updateInputWeights — atualização dos parâmetros do modelo.
O algoritmo do método de distribuição de gradientes de erro reflete o método de propagação para frente, mas em ordem inversa. Recomendo que você revise esse algoritmo de maneira independente no anexo. No entanto, algumas palavras devem ser ditas sobre o método de atualização dos parâmetros do modelo. É nesse método que implementamos a atualização do estado oculto durante o treinamento do modelo.
bool CNeuronSSMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cA.UpdateInputWeights(cHiddenStates.AsObject())) return false; if(!SumAndNormilize(cA.getOutput(), cB.getOutput(), cHiddenStates.getOutput(), iWindowHidden, true)) return false;
Primeiro, ajustamos os parâmetros da camada interna de projeção do estado oculto. Somente depois disso é que atualizamos os valores do estado oculto.
Observe que, nesta etapa, não verificamos o modo de operação do modelo, pois a chamada deste método é permitida apenas durante o processo de treinamento.
Em seguida, chamamos os métodos homônimos dos demais objetos internos que possuem parâmetros treináveis.
if(!cB.UpdateInputWeights(NeuronOCL)) return false; if(!cC.UpdateInputWeights(cAB.AsObject())) return false; //--- return true; }
Ao concluir todas as operações do método, retornamos seu resultado lógico para o programa chamador.
Com isso, finalizamos a análise dos métodos da classe de implementação do SSM. O código completo de todos os seus métodos pode ser consultado no anexo.
2.2 Classe do método Mamba
Acima, implementamos a classe para a camada SSM. Agora podemos avançar para a implementação do algoritmo de alto nível do método Mamba. Para isso, criaremos a classe CNeuronMambaOCL, que herdará a funcionalidade base da camada totalmente conectada CNeuronBaseOCL, assim como a anterior. A estrutura da nova classe é apresentada abaixo.
class CNeuronMambaOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL cXProject; CNeuronConvOCL cZProject; CNeuronConvOCL cInsideConv; CNeuronSSMOCL cSSM; CNeuronBaseOCL cZSSM; CNeuronConvOCL cOutProject; CBufferFloat Temp; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; //--- public: CNeuronMambaOCL(void) {}; ~CNeuronMambaOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMambaOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Aqui, vemos o conjunto familiar de métodos redefiníveis e a declaração de camadas neurais internas, cujas funcionalidades exploraremos durante a implementação dos métodos da classe.
No entanto, nenhuma variável interna é declarada para o armazenamento de constantes. As soluções que permitiram eliminar esse tipo de armazenamento também serão discutidas no processo de implementação.
Como de costume, todos os objetos internos são declarados como estáticos e, portanto, o construtor e o destrutor da classe permanecem vazios. A inicialização dos objetos é realizada no método Init.
bool CNeuronMambaOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
O conjunto de parâmetros aqui é semelhante ao do método homônimo da classe CNeuronSSMOCL analisada anteriormente. Não é difícil deduzir que eles possuem funcionalidades semelhantes.
No corpo do método, chamamos diretamente o método de inicialização da classe base, que lida com os objetos e variáveis herdados.
Como você se lembra da descrição teórica do método Mamba, os dados brutos aqui passam por dois fluxos paralelos. Para ambos os fluxos, realizamos a projeção dos dados, que será executada por camadas convolucionais.
if(!cXProject.Init(0, 0, OpenCL, window, window, window_key + 2, units_count, 1, optimization, iBatch)) return false; cXProject.SetActivationFunction(None); if(!cZProject.Init(0, 1, OpenCL, window, window, window_key, units_count, 1, optimization, iBatch)) return false; cZProject.SetActivationFunction(SIGMOID);
No primeiro fluxo, utilizamos uma camada convolucional e o SSM. No segundo, aplicamos uma função de ativação e os dados são encaminhados para a fusão dos fluxos de informações. Por conseguinte, os tensores devem ter tamanhos compatíveis na saída dos dois fluxos. Para alcançar esse resultado, aumentamos ligeiramente o tamanho da projeção do primeiro fluxo, o que é compensado pela compressão dos dados durante a convolução.
Observe que a função de ativação é usada apenas para a projeção do segundo fluxo.
O próximo passo é inicializar a camada convolucional.
if(!cInsideConv.Init(0, 2, OpenCL, 3, 1, 1, window_key, units_count, optimization, iBatch)) return false; cInsideConv.SetActivationFunction(SIGMOID);
Aqui, realizamos uma convolução independente dentro de cada elemento da sequência. Portanto, definimos o tamanho do tensor do estado oculto como o número de elementos da convolução. Em seguida, adicionamos o número total de variáveis independentes, que equivale ao número de elementos da sequência.
O tamanho da janela de convolução e seu passo correspondem ao aumento na projeção do primeiro fluxo de dados.
Aqui também aplicamos uma função de ativação, o que torna os dados compatíveis em ambos os fluxos de informação.
Seguimos então para o bloco SSM, onde ocorre a seleção dos estados.
if(!cSSM.Init(0, 3, OpenCL, window_key, window_key, units_count, optimization, iBatch)) return false;
No final do algoritmo, para introduzir não linearidade na combinação dos dois fluxos de informação, concatenamos os dados dos fluxos em um único tensor, como feito anteriormente.
if(!cZSSM.Init(0, 4, OpenCL, 2 * window_key * units_count, optimization, iBatch)) return false; cZSSM.SetActivationFunction(None);
Realizamos a projeção dos dados para o tamanho necessário dentro dos elementos individuais da sequência utilizando uma camada convolucional.
if(!cOutProject.Init(0, 5, OpenCL, 2*window_key, 2*window_key, window, units_count, 1, optimization, iBatch)) return false; cOutProject.SetActivationFunction(None);
Adicionamos um buffer para armazenar os resultados intermediários.
if(!Temp.BufferInit(window * units_count, 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false;
Executamos a substituição dos ponteiros para os buffers de dados.
if(!SetOutput(cOutProject.getOutput())) return false; if(!SetGradient(cOutProject.getGradient())) return false; SetActivationFunction(None); //--- return true; }
Por fim, retornamos o resultado lógico das operações realizadas ao programa chamador.
Após a conclusão do trabalho com o método de inicialização da classe, iniciamos a construção dos algoritmos de propagação no método feedForward. Parte do algoritmo já havia sido apresentada durante a criação do método de inicialização. Agora, veremos a implementação do algoritmo no código.
bool CNeuronMambaOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cXProject.FeedForward(NeuronOCL)) return false; if(!cZProject.FeedForward(NeuronOCL)) return false;
Nos parâmetros do método, recebemos um ponteiro para o objeto da camada anterior, cujo buffer contém os dados brutos. No corpo do método, realizamos imediatamente a projeção dos dados recebidos, chamando os métodos de propagação para frente das camadas convolucionais de projeção de dados.
Com isso, podemos considerar concluídas as operações do segundo fluxo de informações. No entanto, ainda precisamos realizar as operações do fluxo principal de dados. Primeiro, aplicamos uma convolução nos dados.
if(!cInsideConv.FeedForward(cXProject.AsObject())) return false;
Depois disso, realizamos a seleção dos estados.
if(!cSSM.FeedForward(cInsideConv.AsObject())) return false;
Agora, com as operações de ambos os fluxos concluídas, combinamos os resultados em um único tensor.
if(!Concat(cSSM.getOutput(), cZProject.getOutput(), cZSSM.getOutput(), 1, 1, cSSM.Neurons())) return false;
Lembramos, então, que não salvamos a dimensionalidade do estado interno de um elemento da sequência. No entanto, isso não é um problema. Sabemos que os tensores de ambos os fluxos de informação têm a mesma dimensionalidade. Assim, ao processarmos um elemento de cada tensor sequencialmente, manteremos a estrutura geral intacta.
Por fim, resta apenas projetar os dados para a dimensionalidade necessária dos resultados.
if(!cOutProject.FeedForward(cZSSM.AsObject())) return false; //--- return true; }
No final do método, retornamos ao programa chamador o resultado lógico das operações realizadas.
Como se pode observar, o algoritmo do método de propagação para frente não é particularmente complexo. O mesmo pode ser dito sobre os métodos de propagação reversa. Por isso, sugiro não nos aprofundarmos na análise detalhada desses algoritmos agora, deixando-os para estudo independente. O código completo desta classe e de todos os seus métodos está disponível no anexo.
2.3 Arquitetura dos modelos
Acima, implementamos nossa visão dos enfoques propostos pelos autores do método Mamba. No entanto, o trabalho realizado deve gerar resultados. Para avaliar a eficiência dos algoritmos implementados, precisamos integrá-los ao nosso modelo. Provavelmente, você já percebeu que os novos blocos serão adicionados à modelo do Codificador do estado do ambiente. Afinal, é esso modelo que treinamos dentro da abordagem de previsão do movimento futuro de preços.
A arquitetura da referido modelo é definida no método CreateEncoderDescriptions.
bool CreateEncoderDescriptions(CArrayObj *&encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Nos parâmetros do método, recebemos um ponteiro para um array dinâmico, no qual registraremos a descrição da arquitetura do modelo criado.
No corpo do método, verificamos a validade do ponteiro recebido e, se necessário, criamos uma nova instância do objeto. Assim, finalizamos o trabalho preparatório e partimos para a criação da descrição da arquitetura do modelo.
A primeira camada é projetada para transmitir os dados brutos para o modelo. Aqui, como de costume, utilizamos uma camada totalmente conectada de tamanho adequado.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Normalmente, transmitimos à modelo os dados brutos tal como os recebemos do terminal. Naturalmente, esses dados pertencem a diferentes distribuições. Sabemos que a eficiência de qualquer modelo aumenta significativamente quando se trabalha com dados de valores compatíveis. Para ajustar os dados brutos diversificados a um formato mais uniforme, utilizamos uma camada de normalização em lotes.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, criamos um bloco composto por três camadas do método Mamba com arquiteturas idênticas. Para isso, elaboramos uma única descrição da arquitetura do bloco e, em seguida, adicionamos essa descrição ao array o número necessário de vezes.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMambaOCL; descr.window = BarDescr; //window descr.window_out = 4 * BarDescr; //Inside Dimension prev_count = descr.count = HistoryBars; //Units descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; for(int i = 2; i <= 4; i++) if(!encoder.Add(descr)) { delete descr; return false; }
Observe que o tamanho da janela de dados analisada é igual ao número de elementos que descrevem um único elemento da sequência, enquanto o tamanho da representação interna foi definido como quatro vezes maior. Isso porque, no método Mamba, os autores recomendam uma projeção expansiva.
O número de elementos da sequência corresponde à profundidade do histórico analisado.
Como mencionado durante a implementação das classes, nesta realização não alocamos canais de informação separados. Contudo, nosso algoritmo trabalha com elementos independentes da sequência. Se for necessário analisar canais independentes, você pode transpor os dados previamente e ajustar os parâmetros da camada correspondente. No entanto, deixaremos essa abordagem para outro experimento.
Mesmo assim, realizaremos a previsão das sequências em canais independentes. Para isso, adicionaremos a transposição dos dados após o bloco Mamba.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = prev_count; descr.window = BarDescr; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Utilizaremos duas camadas convolucionais para prever os valores futuros dos canais independentes.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = prev_count; descr.window_out = 4 * NForecast; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = BarDescr; descr.window = 4 * NForecast; descr.window_out = NForecast; descr.activation = TANH; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Depois, retornaremos os valores previstos ao formato original.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronTransposeOCL; descr.count = BarDescr; descr.window = NForecast; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Adicionaremos a eles as características estatísticas da distribuição dos dados brutos, obtidas durante a normalização.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
O último detalhe de nosso modelo será o ajuste dos resultados no domínio da frequência.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
As arquiteturas dos modelos Ator e Crítico permaneceram inalteradas. Também não houve mudanças nos programas de interação com o ambiente. No entanto, precisávamos realizar pequenas correções nos programas de treinamento das modelos. Isso porque o uso de estados ocultos no bloco SSM exige uma alteração na sequência de fornecimento dos dados brutos, o que é típico de modelos recorrentes. Essas alterações são feitas sempre que utilizamos modelos com estados ocultos, nos quais as informações são acumuladas ao longo do tempo de operação. Recomendo que você analise essas alterações por conta própria no anexo. Lembro que o código de todos os programas e classes utilizados na preparação deste artigo está disponível lá. Assim, finalizamos a análise da implementação dos enfoques propostos e partimos para os testes práticos com dados históricos reais.
3. Testes
Agora, entramos na etapa final: o treinamento das modelos e a avaliação dos resultados alcançados. Treinamos as modelos com dados históricos do ano de 2023, usando o par EURUSD no timeframe H1. Mantivemos os parâmetros padrão de todos os indicadores.
Na primeira etapa, treinamos o modelo do Codificador do estado do ambiente para prever o movimento de preços em um horizonte de planejamento específico. Esse modelo analisa apenas os dados históricos do movimento de preços, ignorando completamente as ações do Ator. Isso nos permite realizar o treinamento completo do modelo utilizando os dados previamente coletados, sem a necessidade de atualizações. No entanto, essa atualização pode ser necessária caso o período histórico de treinamento seja alterado ou ampliado.
O primeiro ponto a destacar é que o modelo demonstrou ser bastante compacto e veloz. O processo de treinamento ocorreu de maneira relativamente estável e eficiente. Além disso, o modelo apresentou resultados interessantes.
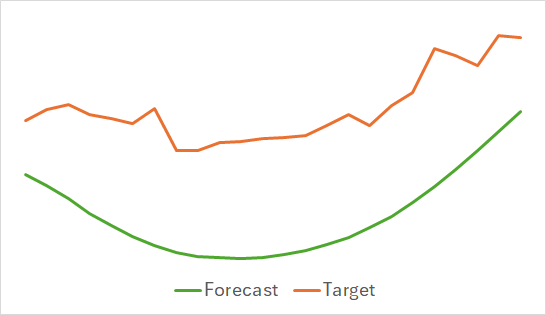
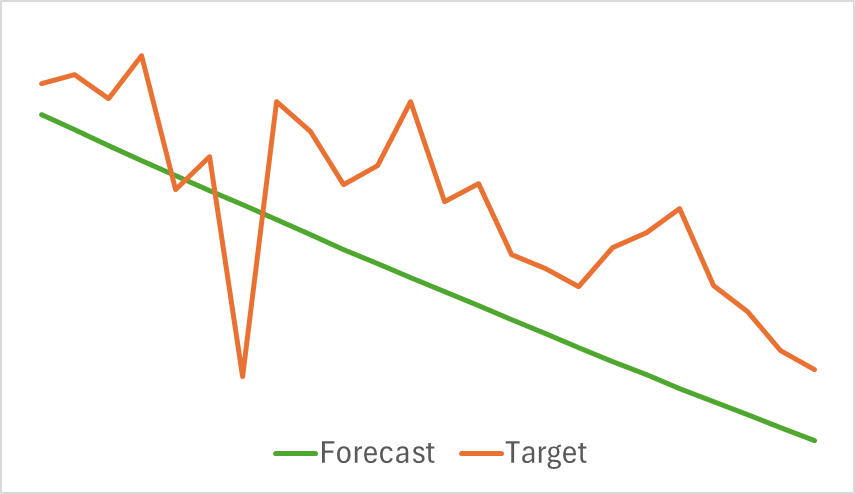
Acima, estão apresentados os resultados da previsão do movimento de preços para as próximas 24 horas. No primeiro caso, a linha de previsão descreve de maneira bastante suave o ponto de mudança da tendência. Já no segundo caso, a linha de previsão indica praticamente de forma linear a tendência atual.
Na segunda etapa, realizamos o treinamento iterativo da política do Ator. Juntamente com isso, treinamos a função de custo do Crítico. O papel do Crítico é orientar o Ator na direção de maior eficiência em sua política.
Como mencionado anteriormente, a segunda etapa do treinamento é iterativa. Isso significa que, durante o treinamento das modelos, atualizamos periodicamente o conjunto de treinamento para incluir dados relevantes à política atual do Ator. A atualização contínua desse conjunto é essencial para o aprendizado correto das modelos.
No entanto, durante o treinamento, não obtivemos uma política com uma tendência clara de crescimento do saldo da conta. De fato, nosso modelo gerou lucro no período de testes de janeiro de 2024, mas não foi possível observar uma tendência clara.
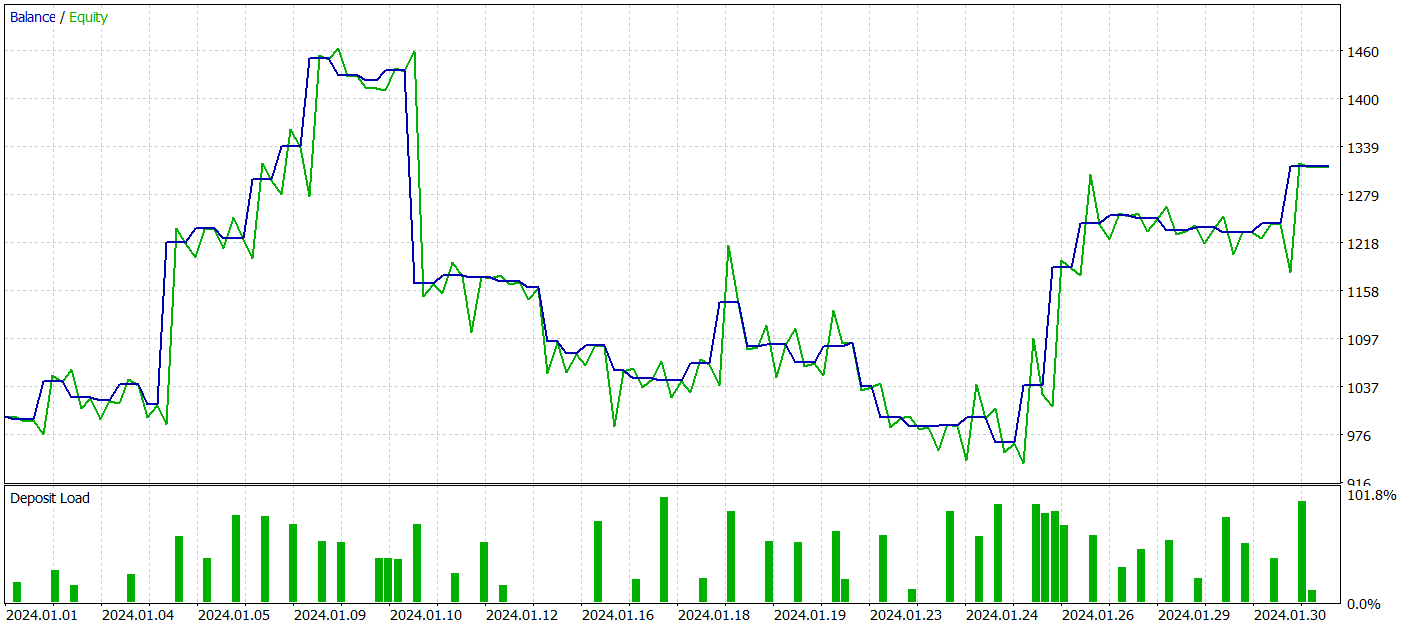
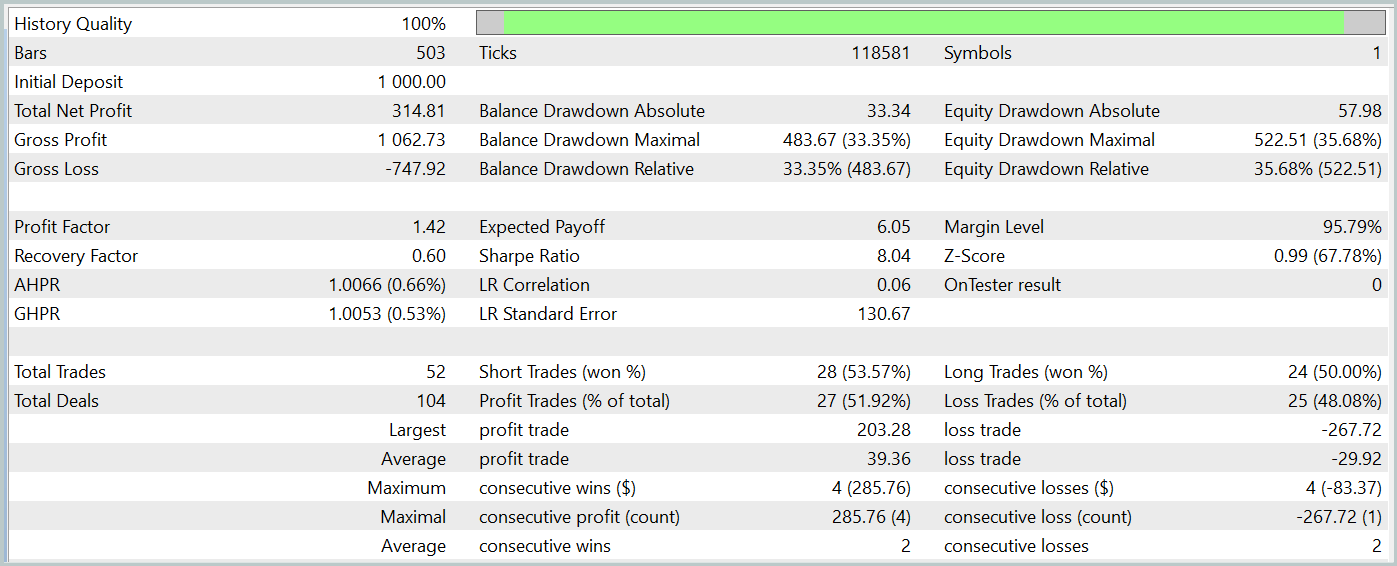
Durante o período de teste, o modelo realizou 52 negociações, das quais 27 foram encerradas com lucro, representando quase 52%. O lucro médio por negociação foi superior à média das perdas (-29,82 contra 39,36). No entanto, a maior perda superou o maior lucro por negociação em 30%. Além disso, foi registrada uma redução de mais de 35% no saldo (Equity). Esses resultados mostram que o modelo precisa de ajustes adicionais.
Chamam atenção os gráficos de lucros e perdas distribuídos por horas e dias.
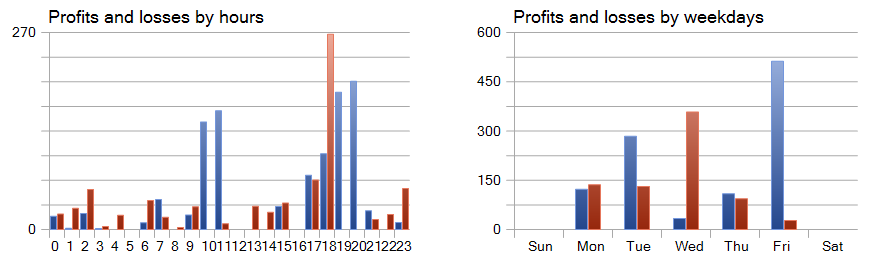
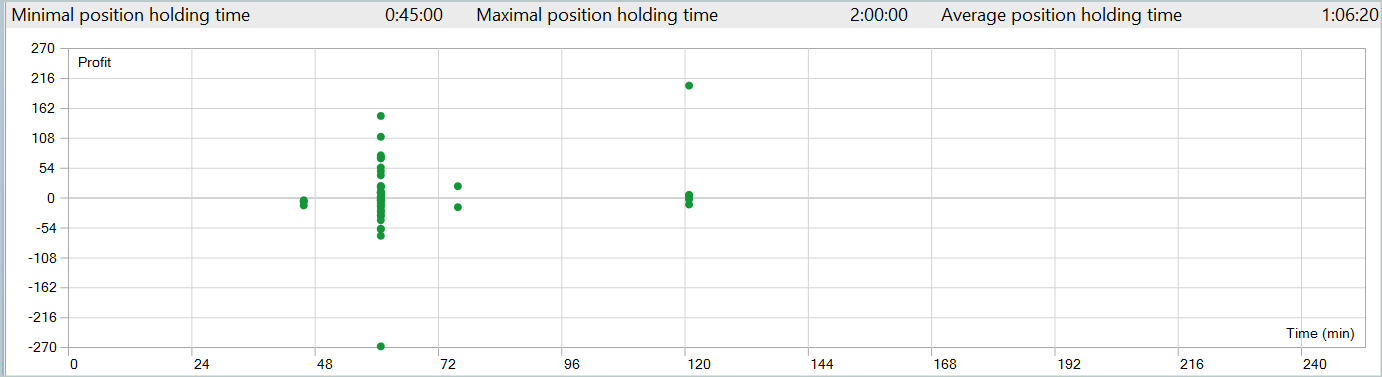
Destacamos positivamente a sexta-feira, enquanto a quarta-feira se mostrou mais desfavorável. Também identificamos períodos intradiários nos quais houve maior concentração de negociações lucrativas e prejudiciais. Esses padrões oferecem insights valiosos. Considerando que a duração média de retenção das posições é pouco superior a uma hora, com um máximo de duas horas, há muito a ser explorado.
Considerações finais
Neste artigo, exploramos o novo método de previsão de séries temporais, o Mamba, que oferece uma alternativa eficiente e de alto desempenho às arquiteturas tradicionais, como o Transformer. Por meio da integração de modelos seletivos de espaço de estados (SSM), o Mamba proporciona alta capacidade de processamento e escalabilidade linear conforme o comprimento da sequência.
Na parte prática do artigo, implementamos nossa visão dos enfoques propostos utilizando MQL5. Treinamos as modelos com dados reais e obtivemos resultados mistos.
Referências
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de Modelos |
| 4 | StudyEncoder.mq5 | Expert Advisor | EA para treinamento do Codificador |
| 5 | Test.mq5 | Expert Advisor | EA para testar o modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15546
 Algoritmo de otimização de migração animal (AMO)
Algoritmo de otimização de migração animal (AMO)
 Analisando exemplos de estratégias de trading no terminal do cliente
Analisando exemplos de estratégias de trading no terminal do cliente
 Métodos de William Gann (Parte I): Criando um indicador de ângulos de Gann
Métodos de William Gann (Parte I): Criando um indicador de ângulos de Gann
 Redes neurais em trading: Injeção de informação global em canais independentes (InjectTST)
Redes neurais em trading: Injeção de informação global em canais independentes (InjectTST)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso