Construção de linhas fractais

Introdução

Fractais são usados por praticamente todos os traders. Contudo, caso você pergunte a eles o que é um fractal, a melhor resposta que você irá obter é que se trata de um indicador no sistema de Bill Williams. Os traders mais avançados dirão que se trata de uma sequência de 5 barras, nas quais, caso o ponto alto da barra média for mais alto do que aqueles das outras barras da sequência, tem-se um fractal para cima, e caso o ponto baixo da barra média for mais baixo do que aqueles das outras barras, tem-se um fractal para baixo. Como diz a famosa frase, "isso é tudo o que eu tenho a dizer sobre a guerra".

Uma breve descrição de fractais, particularmente da sua natureza e de seu uso, é apresentada no livro de Bill Williams chamado "New Trading Dimensions: How to Profit from Chaos in Stocks, Bonds, and Commodities" ("Novas dimensões da negociação: como lucrar com o caos em ações, títulos e produtos"). Também pode-se encontrar algumas informações no artigo de Chekulaev chamado "Fractais" (em russo). As fórmulas matemáticas são bem descritas no livro de Shiryaev chamado "Fundamentos da matemática estocástica" (em russo).

Uso de fractais

Há dois tipos de penetração fractal a serem marcados: um simples, no qual o preço excede o nível do fractal para cima (cai para baixo do nível do fractal para baixo). Neste caso, seria melhor esperar pelo preço de fechamento e abrir uma posição na abertura da próxima barra.

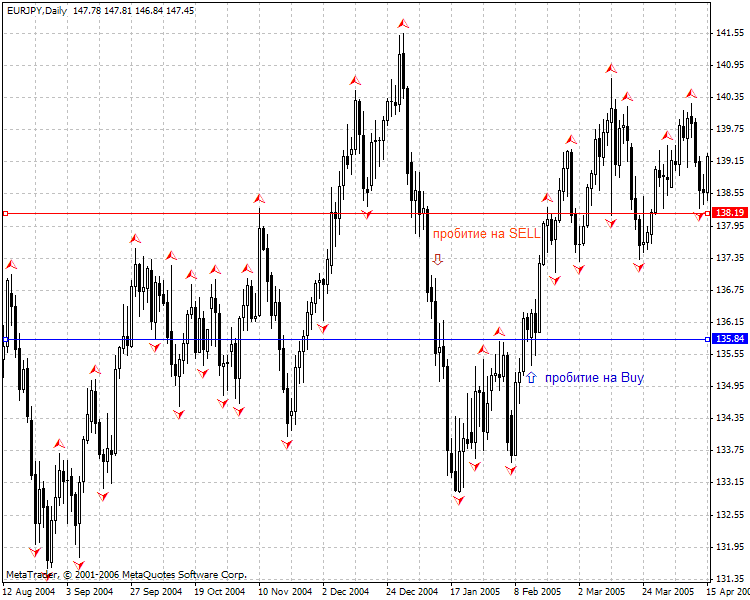
Os fractais respectivos de compra e venda são marcados com setas na figura acima, onde nós consideramos a penetração fractal simples. Uma penetração complexa utiliza 2 fractais: o último e o penúltimo. Eles são unidos por uma linha reta que, espera-se, será penetrada pelo preço de fechamento.

Os pontos de entrada nos quais a linha fractal é penetrada são marcados pelas setas azul e vermelha. O ambiente de desenvolvimento do MQL4 irá nos ajudar a entender melhor a ideologia fractal.Vamos definir um problema para testar fractais:

• desenhe fractais de compra/venda;
• desenhe níveis de penetração horizontais;
• desenhe linhas fractais;
• marque os pontos de entrada previstos com setas.

Fractais de compra/venda

Esta deve ser a parte mais simples. Nós também devemos considerar o indicador iFractal, disponível no MQL4 (no Omega, eu mesmo tive que escrever este indicador, o que foi bastante difícil devido às propriedades do Omega). Os exemplos de como escrever este indicador podem ser encontrados na base de códigos.

Níveis horizontais de penetração

Vamos usar linhas horizontais padrão. Nós vamos especificar o preço de um fractal como uma coordenada de preço, e a data de formação do fractal e o tempo atual serão apresentados como coordenadas de tempo.

ObjectCreate("SimpleUp"+Up,OBJ_TREND,0,bufUpDate[Up],
             bufUpPrice[Up],Time[i-1],bufUpPrice[Up]);
ObjectSet("SimpleUp"+Up,OBJPROP_COLOR,Aqua);
ObjectSet("SimpleUp"+Up,OBJPROP_RAY,True);

Linhas fractais

A forma mais simples parece ser desenhar linhas de tendência através de 2 pontos. Nós criamos um raio da linha e esperamos pela penetração. Contudo, de fato não parece ser possível comparar o preço de fechamento com o valor do preço na linha fractal, pois a função ObjectGet pode devolver apenas valores de pontos que formaram a linha fractal. Então o que devemos fazer?

Nós devemos lembrar da geometria analítica. Nós temos 2 pontos, então temos uma equação de linha reta. E, dado que nós conhecemos as coordenadas de tempo, podemos facilmente obter o valor do preço a partir da equação de linha reta. A equação de linha reta canônica possui a seguinte aparência:

Nós vamos substituir o preço e o tempo, ao invés de x e y. A realização disso é dada na função LevelCalculate que calcula o nível de penetração e, ao mesmo tempo, define novas coordenadas da linha fractal a serem configuradas através do uso da função ObjectSet.

ObjectCreate("LineUp"+Up,OBJ_TREND,0,bufUpDate[Up],
             bufUpPrice[Up],bufUpDate[Up-1],bufUpPrice[Up-1]); 
ObjectSet("LineUp"+Up,OBJPROP_COLOR,Blue);
ObjectSet("LineUp"+Up,OBJPROP_RAY,False);

Colocação de setas

Nós construímos todas as linhas necessárias no ciclo e então as comparamos aos preços atuais. Caso ele penetre uma linha simples, nós colocamos uma seta amarela. Caso ele penetre uma linha fractal, a seta para compra será azul, e para venda será vermelha.

Tudo isso é realizado como o indicador FractalLines.mq4.

//+------------------------------------------------------------------+
//|                                                 FractalLines.mq4 |
//|                      Copyright © 2006, MetaQuotes Software Corp. |
//|                                        https://www.metaquotes.net/ |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2006, MetaQuotes Software Corp."
#property link      "https://www.metaquotes.net/"
 
#property indicator_chart_window
#property indicator_buffers 2
#property indicator_color1 Blue
#property indicator_color2 Red
//---- input parameters
extern int       lines=5;  //The amount of visible fractal lines
extern int       MaxFractals=10000; // :)
extern bool       ShowHorisontalLines=true;
extern bool       ShowFractalLines=true; 
//---- buffers
double ExtMapBuffer1[];
double ExtMapBuffer2[];
//--- my variables
double bufUpPrice[10000];  //price array of Up fractals
double bufUpDate[10000];   //date array of Up fractals
double bufDownPrice[10000];   //price array of Down fractals
double bufDownDate[10000]; //date array of Down fractals
int Up = 0; //counter of Up fractals
int Down = 0;  //counter of Down fractals
 
//The function calculates the price value of penetration of the fractal line by the simplest
//equations of analytic geometry
double LevelCalculate(double Price1, double Time1, double Price2, 
                     double Time2, double NewTime)
{
   double level;
   if (Time2!=Time1)// Just in case, to avoid zero divide.
   {
      level=(NewTime-Time1)*(Price2-Price1)/(Time2-Time1)+Price1;
   }
   else
   { 
      return(Price2);
   }
   return(level);
}
 
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int init()
  {
//---- indicators
   SetIndexStyle(0,DRAW_ARROW);
   SetIndexArrow(0,217);
   SetIndexBuffer(0,ExtMapBuffer1);
   SetIndexEmptyValue(0,0.0);
   SetIndexStyle(1,DRAW_ARROW);
   SetIndexArrow(1,218);
   SetIndexBuffer(1,ExtMapBuffer2);
   SetIndexEmptyValue(1,0.0);
//----
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator deinitialization function                       |
//+------------------------------------------------------------------+
int deinit()
  {
//----
   
//----
   return(0);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int start()
  {
   int    counted_bars=IndicatorCounted();
//---- the last calculated bar will be recalculated   
   if(counted_bars > 0) 
       counted_bars--;
   int limit = Bars - counted_bars;
// We will rather place arrows at the moment of penetration of fractal lines, 
// estimate efficiency
 // The idea was borrowed from Rosh, hopefully he will not be offended by this :)    
  string arrowName; // here, we will give the arrow a unique name
  
  //The number of the penetrated fractal
  //Penetration of the fractal line
  int FractalUp = 0;
  int FractalDown = 0;
  //Simple penetration of a fractal
  int SimpleFractalUp = 0;
  int SimpleFractalDown = 0;
  
  double BuyFractalLevel = 0;  //penetration level of the Up fractal line
  double SellFractalLevel = 0; //penetration level of the Down fractal line
  double buf = 0; // buffer value of fractal being available; if it is 0, there is no fractal at all
 
//---- the main loop       
   for(int i = limit; i>0; i--)
   {   
   
       //Draw simple fractal levels
       
       //Define the current fractal levels 
 
         BuyFractalLevel=LevelCalculate(bufUpPrice[Up],bufUpDate[Up],
                   bufUpPrice[Up-1],bufUpDate[Up-1],Time[i]);
         //Move the second coordinate of the Up fractal line                              
         ObjectSet("LineUp"+Up,OBJPROP_TIME1,Time[i]);
         ObjectSet("LineUp"+Up,OBJPROP_PRICE1,BuyFractalLevel); 
         SellFractalLevel=LevelCalculate(bufDownPrice[Down],
                          bufDownDate[Down],bufDownPrice[Down-1],
                          bufDownDate[Down-1],Time[i]);
         //Move the second coordinate of the Down fractal line                               
         ObjectSet("LineDown"+Down,OBJPROP_TIME1,Time[i]);
         ObjectSet("LineDown"+Down,OBJPROP_PRICE1,SellFractalLevel);
         
      //Search for a simple penetration
         if (Close[i]>ObjectGet("SimpleUp"+Up,OBJPROP_PRICE1)&&
                          (Up>SimpleFractalUp))
         {
            arrowName="SimleUpArrow"+Up;
            ObjectCreate(arrowName,OBJ_ARROW,0,Time[i-1],
                         Low[i-1]-Point*10);
            ObjectSet(arrowName,OBJPROP_ARROWCODE,241);
            ObjectSet(arrowName,OBJPROP_COLOR,Yellow);
            SimpleFractalUp=Up;             
         }
         
         if (Close[i]<ObjectGet("SimpleDown"+Down,OBJPROP_PRICE1)&&
                          (Down>SimpleFractalDown))
         {
            arrowName="SimleUpArrow"+Down;
            ObjectCreate(arrowName,OBJ_ARROW,0,Time[i-1],
                         High[i-1]+Point*10);
            ObjectSet(arrowName,OBJPROP_ARROWCODE,242);
            ObjectSet(arrowName,OBJPROP_COLOR,Yellow);
            SimpleFractalDown=Down;             
         }                                                                                                                          
 
      //Search for a complex penetration
        if ((Close[i]>BuyFractalLevel)&&(Up>FractalUp)) 
         {
            //Put an up-arrow
            arrowName="UpArrow"+Up;
            ObjectCreate(arrowName,OBJ_ARROW,0,Time[i-1],
                         Low[i-1]-Point*10);
            ObjectSet(arrowName,OBJPROP_ARROWCODE,241);
            ObjectSet(arrowName,OBJPROP_COLOR,Blue);
            FractalUp=Up;        
         }
                                          
        if ((Close[i]<SellFractalLevel)&&(Down>FractalDown))
         {
            //Put a down-arrow
            arrowName="DownArrow"+Down;
            ObjectCreate(arrowName,OBJ_ARROW,0,Time[i-1],
                         High[i-1]+Point*10);
            ObjectSet(arrowName,OBJPROP_ARROWCODE,242);
            ObjectSet(arrowName,OBJPROP_COLOR,Red); 
            FractalDown=Down;       
         }
        //Draw the Up fractal itself
        ExtMapBuffer1[i] = iFractals(NULL, 0, MODE_UPPER, i);
        
        //If it is available, place it in the array of fractals
        buf = iFractals(NULL, 0, MODE_UPPER, i);
        if (buf!=0)
        {
            Up++;
            bufUpPrice[Up]=iFractals(NULL, 0, MODE_UPPER, i);
            bufUpDate[Up]=Time[i];
            //The current fractal penetration level - fractal itself
            BuyFractalLevel=bufUpPrice[Up];
            
            if (Up>1)
            
            {
               //Simple fractal
               ObjectCreate("SimpleUp"+Up,OBJ_TREND,0,bufUpDate[Up],
                   bufUpPrice[Up],Time[i-1],bufUpPrice[Up]);
      ObjectSet("SimpleUp"+Up,OBJPROP_COLOR,Aqua);
      ObjectSet("SimpleUp"+Up,OBJPROP_RAY,True);   
               //Draw fractal lines on 2 coordinates
               ObjectCreate("LineUp"+Up,OBJ_TREND,0,bufUpDate[Up],
                  bufUpPrice[Up],bufUpDate[Up-1],bufUpPrice[Up-1]); 
      ObjectSet("LineUp"+Up,OBJPROP_COLOR,Blue);
      ObjectSet("LineUp"+Up,OBJPROP_RAY,False);
               //Remove the outdated lines
               if (Up>lines+1)
               {
                  ObjectDelete("LineUp"+(Up-lines));
                  ObjectDelete("SimpleUp"+(Up-lines));                  
               }
            }     
        }
         //A similar block, but for Down fractals
        ExtMapBuffer2[i] = iFractals(NULL, 0, MODE_LOWER, i);
        buf = iFractals(NULL, 0, MODE_LOWER, i);    
        if (buf!=0)
        {
            Down++;
            bufDownPrice[Down]=iFractals(NULL, 0, MODE_LOWER, i);
            bufDownDate[Down]=Time[i];
            SellFractalLevel=bufDownPrice[Down];
                                         
            if (Down>1)
            
            {
               ObjectCreate("SimpleDown"+Down,OBJ_TREND,0,bufDownDate[Down],
                   bufDownPrice[Down],Time[i-1],bufDownPrice[Down]);        
               ObjectSet("SimpleDown"+Down,OBJPROP_COLOR,LightCoral);
               ObjectSet("SimpleDown"+Down,OBJPROP_RAY,True);
                                  
               ObjectCreate("LineDown"+Down,OBJ_TREND,0,
                            bufDownDate[Down],bufDownPrice[Down],
                            bufDownDate[Down-1],bufDownPrice[Down-1]);        
               ObjectSet("LineDown"+Down,OBJPROP_COLOR,Red);
               ObjectSet("LineDown"+Down,OBJPROP_RAY,False);
               if (Down>lines+1)
               {
                  ObjectDelete("LineDown"+(Down-lines));
                  ObjectDelete("SimpleDown"+(Down-lines));
               }            
            }
     
        }           
        if (!ShowHorisontalLines)
        {   
            ObjectDelete("SimpleDown"+Down);              
            ObjectDelete("SimpleUp"+Up);                
        }
        if (!ShowFractalLines)
        {
            ObjectDelete("LineDown"+Down);        
            ObjectDelete("LineUp"+Up);
        }          
     }   
//----
   return(0);
  }
//+----------------------------------------------------------------- 

Linhas antigas devem ser removidas, do contrário o gráfico ficará parecido com uma paleta. Há algumas configurações adicionais fornecidas no indicador, como visibilidade ou quantidade de linhas. O resultado das atividades do indicador é dado abaixo:

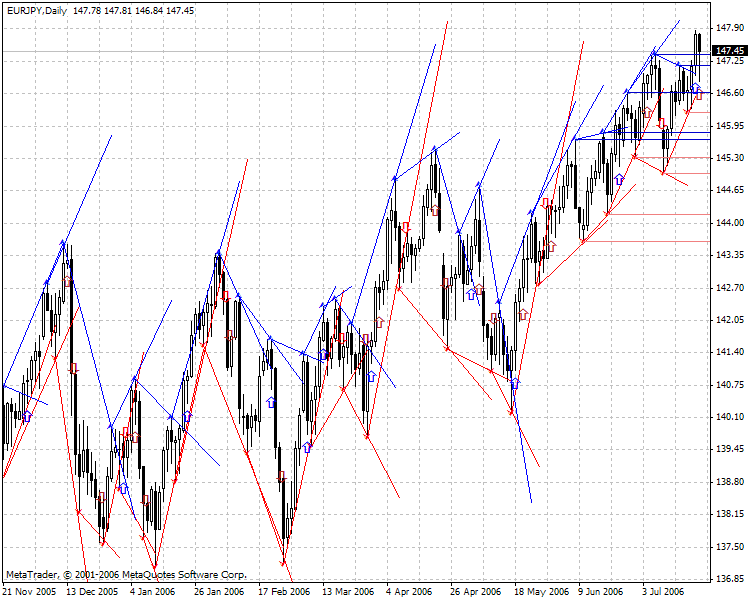
Isso deve empolgar aqueles que amam fractais!