Redes neurais de maneira fácil (Parte 28): algoritmo de gradiente de política

Conteúdo

• Introdução
• 1. Particularidades ao implementar gradiente de política
• 2. Fundamentos do treinamento do modelo de política
• 3. Implementação do treinamento de modelo
• 3.1 Implementando SoftMax
• 3.2 Criando o EA para treinar o modelo
• 4. Prova do modelo treinado no testador de estratégia
• Considerações finais
• Referências
• Programas utilizados no artigo

Introdução

Continuamos nosso mergulho nos métodos de aprendizado por reforço. No artigo anterior, nos iniciamos no método de aprendizado Q profundo. Ele aproxima a função de utilidade de uma ação usando uma rede neural. Como resultado, obtemos uma ferramenta que serve para prever a recompensa esperada ao executar uma ação específica em um determinado estado do sistema. Depois dessa previsão, o agente executa uma ação com base na política adotada e no valor da recompensa esperada. Não discutimos explicitamente o uso da política, mas assumimos a escolha da ação com a recompensa máxima esperada. Isso decorre da fórmula de Bellman e do objetivo geral do aprendizado por reforço, que é maximizar a recompensa da sessão analisada.

Note que, ao estudar os métodos de aprendizado por reforço, nunca mencionamos o retreinamento do modelo. Na verdade, se você observar o modelo de aprendizado por reforço, o objetivo do agente é estudar o ambiente da melhor maneira possível. Assim, quanto melhor o agente conhecer o ambiente, mais bem-sucedida será sua performance.

Mas quando você lida com um ambiente volátil como o mercado, às vezes você percebe que não há limite para sua variabilidade. Ele não possui 2 estados idênticos. E, mesmo que os estados atuais sejam semelhantes, vamos entrar em estados totalmente opostos no próximo passo.

A aproximação da função Q nos dá apenas a recompensa média esperada sem levar em conta a dispersão de valores e a probabilidade de uma recompensa positiva. E a utilização de uma estratégia gananciosa com uma escolha de máxima recompensa dá sempre uma escolha precisa de ação. Por um lado, facilita o trabalho do nosso agente. Mas tal estratégia só dá frutos enquanto nosso agente não estiver em algum tipo de confronto com o ambiente. Quando isto acontece, suas ações se tornam previsíveis para o ambiente, podendo este desenvolver medidas para contrariar as ações do agente e alterar a política de recompensas. E o agente continuará a usar a função Q previamente aproximada, que não corresponderá mais ao ambiente alterado.

Para solucionar problemas desse gênero, têm sido propostos métodos que não se aproximam da política de recompensa do ambiente. E eles desenvolvem sua própria estratégia de comportamento. É a tais métodos que pertence o gradiente de política, que proponho apresentar hoje.

1. Particularidades ao implementar gradiente de política

Quando demos início ao nosso estudo sobre o aprendizado por reforço, dissemos que o agente interage com o ambiente e realiza ações de acordo com sua estratégia. Isso resulta em uma transição de um estado para outro. Assim, para cada transição, o agente recebe uma certa recompensa proporcionada pelo ambiente, e o valor dessa recompensa é usado pelo agente para avaliar a utilidade da ação realizada. O método do gradiente de política envolve o desenvolvimento de uma estratégia de comportamento do agente.

Obviamente, não definiremos explicitamente a estratégia do agente, como pode ser observado durante o DQN. Em vez disso, apenas fazemos uma suposição sobre a existência de uma certa função matemática de política P, que avalia o estado atual do ambiente e retorna a melhor ação realizaa pelo agente. Como se pode observar, essa abordagem nos permite esquecer todas as dificuldades de aproximar a função Q. E, ao mesmo tempo, podemos nos esquecer de especificar uma política explícita quanto ao comportamento do agente, como se escolhêssemos uma ação com uma recompensa máxima esperada (estratégia gananciosa).

Claro, tudo tem um custo. Por isso, ao invés de aproximar a função Q, teremos que aproximar a função P de política de nosso agente. Este artigo se concentrará no método de gradiente de política estocástico. Ele assume que nossa função de política, ao avaliar o estado atual do ambiente, retorna a distribuição de probabilidade de receber uma recompensa positiva ao executar a ação correspondente.

Quando isso acontece, assumimos que as ações de nosso agente são distribuídas uniformemente. E para selecionar uma ação específica, basta um agente amostrar um valor de entre uma distribuição normal com probabilidades dadas. Claro, podemos usar a estratégia gananciosa e escolher a ação com maior probabilidade. Mas é a amostragem que adiciona variabilidade ao comportamento do nosso agente. E uma probabilidade maior aumenta a frequência de escolha dessa ação específica.

Lembre que, anteriormente, ao treinar modelos por reforço, introduzimos um hiperparâmetro que é responsável pelo equilíbrio entre exploração e uso. No caso da utilização do método do gradiente de política estocástico, esse equilíbrio é regulado pelo modelo no processo de aprendizado justamente graças ao uso de amostragem de ações do agente com uma dada probabilidade. No início do treinamento do modelo, as probabilidades de todas as ações são quase iguais. Isso permite que o modelo explore o ambiente estudado o máximo possível. No processo de estudo do ambiente, aumentamos a probabilidade de ações que levem à maximização da lucratividade, e reduzimos as probabilidades de escolha para as demais ações. Assim, o equilíbrio entre exploração e uso muda em favor da escolha das ações mais lucrativas, o que permite construir uma estratégia com o máximo de lucratividade.

Para aproximar a função P de política de agente, usaremos uma rede neural. E, como se pode imaginar, visto que precisamos determinar a melhor ação do agente a partir dos dados de entrada do estado atual do ambiente, podemos considerar essa tarefa como um problema de classificação. Onde cada ação é uma classe separada de estados iniciais. E aqui, como mencionado anteriormente, precisamos obter na saída da camada neural uma representação probabilística da atribuição do estado do ambiente a um determinado estado.

De certa maneira, a representação probabilística restringe o valor resultante. Elas devem ser normalizadas entre 0% e 100%. E a soma de todas as probabilidades deve ser 100%. No campo do aprendizado de máquina, é comum usar frações de um em vez de porcentagens. E com esta representação temos uma restrição de faixa de valores de 0 a 1, e a soma de todos os valores é igual a 1. Podemos chegar a esse resultado usando a função SoftMax, que possui a seguinte fórmula matemática.

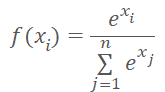
Anteriormente, já nos familiarizamos com essa função, quando nos inicíamos nos métodos de agrupamento de dados. Mas se, ao estudar métodos de aprendizado não supervisionados, procurássemos semelhanças nos dados de entrada para determinar a classe, agora iremos distribuir o estado do ambiente em ações (classes) dependendo da recompensa recebida. E a função SoftMax satisfaz plenamente nossos requisitos. Ela permite que os resultados da rede neural sejam totalmente convertidos em valores dentro do domínio das probabilidades, e, além disso, é diferenciável ao longo de toda a gama de valores. O que é muito importante para treinar nosso modelo.

2. Fundamentos do treinamento do modelo de política

Agora vamos falar um pouco sobre os fundamentos do treinamento do modelo de aproximação da função de política. A questão é que quando treinávamos o modelo DQN, o ambiente nos devolveu uma recompensa em cada nova condição. E treinamos o modelo para prever a recompensa esperada com o mínimo de erro. O que não era muito diferente das abordagens usadas anteriormente com a aprendizado supervisionado.

No caso de aproximar a função P de política de agente a cada novo estado, também recebemos uma recompensa do ambiente. Mas queremos prever a melhor ação, não a recompensa. O sinal de recompensa só pode nos mostrar o impacto da ação atual no resultado. E vamos treinar o modelo para aumentar a probabilidade de escolher uma ação com recompensa positiva e diminuir a probabilidade de escolher uma ação com recompensa negativa.

E aqui devemos lembrar que estamos treinando um modelo de predição de probabilidade. Como mencionado acima, os valores das probabilidades previstas são limitados ao intervalo de 0 a 1. O que não é de modo algum comparável à recompensa recebida. Eles podem ser tanto positivos quanto negativos. Aqui usamos a seguinte lógica. Como precisamos maximizar a probabilidade de escolher ações com uma recompensa positiva, para tais ações definiremos o valor alvo como "1". Assim, o erro do modelo será definido como o desvio da probabilidade de ação prevista em relação a 1. O uso do desvio nos permite utilizar o método gradiente descendente já construído para treinar nosso modelo de aproximação de função de política, uma vez que, minimizando o desvio em relação a 1, maximizamos a probabilidade de escolher uma ação com recompensa positiva.

Também precisamos prestar atenção na escolha da função de perda do nosso modelo. Aqui também podemos recorrer aos métodos de aprendizado supervisionado e lembrar que, para problemas de classificação, podemos usar a função de entropia cruzada.

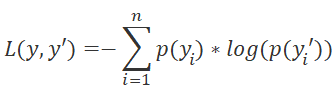
onde p(y) é os valores verdadeiros da distribuição e p(y') é os valores previstos do nosso modelo.

O uso do logaritmo também é de grande importância para prever eventos subsequentes. Sabemos pela teoria da probabilidade que a probabilidade de ocorrência de dois eventos sucessivos é igual ao produto das probabilidades desses eventos. E para todos os logaritmos, a propriedade é verdadeira.

Isso nos permite mudar entre o produto das probabilidades e a soma de seus logaritmos. O que torna o treinamento do nosso modelo mais estável.

Como no caso do treinamento do DQN, para receber as recompensas, nosso agente passa por uma sessão completa com parâmetros fixos. Salvamos os estados, ações e recompensas no buffer. E fazemos uma retropropagação do modelo usando os dados acumulados.

Observe que, como não temos uma função de utilidade de ação, a substituímos pela soma dos valores obtidos durante a sessão. Para cada estado, o valor da função Q é a soma das recompensas sucessivas até o final da sessão.

O treinamento do modelo é repetido até que o nível de erro desejado ou o número máximo de sessões de treinamento seja atingido.

3. Implementação de treinamento de modelo

Depois de estudar os aspectos teóricos do método, procedemos à sua implementação usando MQL5. Primeiro, vamos implementar a função SoftMax. Anteriormente, não a implementávamos como função de ativação, por conta das suas peculiaridades a nível de funcionamento. Agora, para não fazer alterações substanciais em objetos criados anteriormente, proponho implementá-la como uma camada separada de nosso modelo.

3.1 Implementando SoftMax

Para tanto, criaremos uma nova classe CNeuronSoftMaxOCL como herdeira da classe base dos neurônios CNeuronBaseOCL.

class CNeuronSoftMaxOCL    :  public CNeuronBaseOCL
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; }

public:
                     CNeuronSoftMaxOCL(void) {};
                    ~CNeuronSoftMaxOCL(void) {};
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);   
   virtual bool      calcOutputGradients(CArrayFloat *Target, float error) override;
   //---
   virtual int       Type(void) override  const   {  return defNeuronSoftMaxOCL; }
  };

A nova classe não requer a criação de buffers separados. Além disso, ela não utiliza todos os buffers da classe pai, sobre os quais falaremos um pouco mais adiante. Portanto, o construtor e o destruidor da classe ficam vazios. Pela mesma razão, não substituiremos o método de inicialização de nossa classe. Essencialmente, precisaremos apenas substituir os métodos de propagação feedForward de distribuição de gradiente de erro ecalcOutputGradients.

Além disso, por conta do uso da nova função de perda, redefiniremos o método para calcular o erro do modelo e seu gradiente calcOutputGradients.

E, claro, substituiremos o método de identificação da classe Type.

Vamos começar com a organização do processo de propagação. Como antes, realizaremos todas as operações computacionais no modo multi-thread usando a tecnologia OpenCL. Bem, pimeiro vamos criar um novo kernel SoftMax_FeedForward no programa OpenCL. Nos parâmetros do kernel, passaremos ponteiros para os buffers de dados de entrada e de resultados, bem como o tamanho desses buffers. A avaliação da função não requer nenhum parâmetro adicional.

No corpo do kernel, como sempre, definimos o identificador do thread, que serve como um ponteiro para o elemento correspondente do array de dados de entrada e de saída. Como esta é uma implementação da função de ativação, o tamanho dos buffers de entrada e de saída são iguais. E, consequentemente, o ponteiro para os elementos de ambos os buffers será mesmo.

__kernel void SoftMax_FeedForward(__global float *inputs,
                                  __global float *outputs,
                                  const ulong total)
  {
   uint i = (uint)get_global_id(0);
   uint l = (uint)get_local_id(0);
   uint ls = min((uint)get_local_size(0), (uint)256);
//---
   __local float temp[256];

É importante notar que o cálculo da função SoftMax requer a determinação da soma dos valores exponenciais de todos os elementos do buffer de dados de entrada. Não gostaríamos de repetir o cálculo deste valor em cada thread. Além disso, sim gostaríamos de distribuir o processo de cálculo desse valor entre vários threads. Mas aqui há o problema de sincronizar o trabalho de vários threads e trocar dados entre eles. A tecnologia OpenCL não permite o envio de dados de um thread para outro. Mas permite, dentro de grupos de trabalho separados, criar variáveis e arrays comuns na memória local. E essa teconologia também oferece a função barrier(CLK_LOCAL_MEM_FENCE) para sincronização de threads dentro do grupo de trabalho. Usaremos esse conjunto de ferramentas.

Desta forma, enquanto definimos o ID de thread no espaço global de tarefas, vamos definir o ID de thread no grupo de trabalho. E declaramos imediatamente um array na memória local. Nós o usaremos para trocar dados entre threads do grupo de trabalho ao calcular a soma total dos valores exponenciais.

A dificuldade está no fato do OpenCL não permitir o uso de arrays dinâmicos na memória local. E somos forçados a determinar o tamanho do array no estágio de criação do kernel. Com esse tamanho, limitamos o número de threads envolvidos na soma dos valores exponenciais.

O próprio processo de soma de valores exponenciais é realizado a partir de 2 laços sucessivos. No corpo do primeiro loop, cada thread participante do processo de soma percorrerá todo o vetor de valores iniciais com um incremento igual ao número de threads de soma e coletará sua parte da soma dos valores exponenciais. Assim, distribuiremos uniformemente todo o processo de soma entre todos os threads. E cada um deles armazenará seu valor no elemento correspondente do array local.

   uint count = 0;
   if(l < 256)
      do
        {
         uint shift = count * ls + l;
         temp[l] = (count > 0 ? temp[l] : 0) + (count * ls + l < total ? exp(inputs[shift]) : 0);
         count++;
        }
      while((count * ls + l) < total);
   barrier(CLK_LOCAL_MEM_FENCE);

Em dado estágio, sincronizamos os threads após a conclusão das iterações do loop.

Em seguida, precisamos coletar a soma de todos os elementos do array local em um único valor. Para fazer isso, realizamos o segundo laço. Aqui dividimos o tamanho do array local pela metade e somamos os valores aos pares. Obviamente, cada operação de adição de 2 valores será executada por um thread separado. Depois disso, repetimos as iterações do loop, dividindo o número de elementos pela metade e somando os elementos aos pares. As iterações do loop são repetidas até obtermos a soma total dos valores no elemento do array com índice "0".

   count = ls;
   do
     {
      count = (count + 1) / 2;
      if(l < 256)
         temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0);
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Como se pode ver, cada nova iteração do loop só pode começar após a conclusão das operações de todos os threads participantes. Portanto, realizamos a sincronização após cada iteração do loop.

É importante observar aqui que a arquitetura OpenCL fornece apenas sincronização total de threads. E todos os elementos do grupo de trabalho devem chegar ao respetivo operador barrier. Caso contrário, o programa travará. Portanto, ao preparar um programa, precisamos ter muito cuidado com os pontos de sincronização de threads. Não é altamente recomendável defini-los no corpo de operadores condicionais quando o algoritmo do programa permitir que pelo menos um thread ignore os pontos de sincronização.

Depois de concluir as iterações dos loops acima, obtivemos a soma de todos os valores exponenciais dos dados de entrada e podemos concluir o processo de normalização dos dados. Para isso, organizaremos outro laço, no qual preencheremos o buffer de dados de entrada com os valores correspondentes.

   float sum = temp[0];
   if(sum != 0)
     {
      count = 0;
      while((count * ls + l) < total)
        {
         uint shift = count * ls + l;
         outputs[shift] = exp(inputs[shift]) / (sum + 1e-37f);
         count++;
        }
     }
  }

Assim concluímos o trabalho no kernel de propagação e procedemos à criação de kernels de retropropagação.

Começaremos criando kernels de retropropagação com distribuição do gradiente através da função SoftMax. Aqui devemos prestar atenção que a principal característica desta função é a normalização da soma de todos os valores dos resultados em "1". Portanto, alterar apenas um valor na entrada da função de ativação provoca o recálculo de todos os valores do vetor de resultados. Da mesma forma, ao distribuir o gradiente de erro, cada elemento dos dados de entrada deve receber sua parcela do erro a partir de cada elemento do vetor de resultados. A fórmula matemática para a influência de cada elemento dos dados de entrada no resultado é apresentada a seguir. Temos que implementá-la no kernel SoftMax_HiddenGradient.

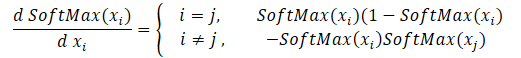
Nos parâmetros, o kernel recebe ponteiros para 3 buffers de dados. Buffers de resultados após um propagação, gradientes provenientes da camada anterior ou da função de perda. Bem como o buffer de gradientes da camada anterior, no qual escreveremos os resultados deste kernel.

No corpo do kernel, definimos o ID do thread e o número total de fluxos, que nos apontará para um elemento de array a fim de registrar o resultado do thread atual e o tamanho dos buffers.

Em seguida, prepararemos 2 variáveis privadas. Em uma copiaremos o valor do elemento correspondente do vetor de resultados da propagação. E a segunda vamos declará-la para coletar os resultados do trabalho do thread atual. O uso de variáveis privadas é causado pelas especificidades da arquitetura OpenCL dos dispositivos. O acesso a variáveis privadas é muito mais rápido do que operações semelhantes com buffers na memória global. Portanto, essa abordagem melhora o desempenho geral do kernel.

A seguir, em um laço coletamos o gradiente de erro de todos os elementos dos resultados de acordo com a fórmula acima. Depois que as operações de loop são concluídas, passamos o valor de gradiente acumulado para o elemento correspondente do buffer de gradiente da camada anterior e encerramos o kernel.

__kernel void SoftMax_HiddenGradient(__global float* outputs,
                                    __global float* output_gr,
                                    __global float* input_gr)
  {
   size_t i = get_global_id(0);
   size_t outputs_total = get_global_size(0);
   float output = outputs[i];
   float result = 0;
   for(int j = 0; j < outputs_total; j++)
      result += outputs[j] * output_gr[j] * ((float)(i == j ? 1 : 0) - output);
   input_gr[i] = result;
  }

Agora resta implementar o kernel para determinar o gradiente de erro da função de perda SoftMax_OutputGradient. Lembre que, neste caso, usamos LogLoss como uma função de perda.

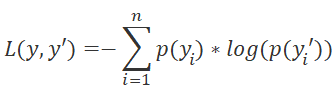
Como distribuímos os gradientes aos elementos da ação correspondente, também calcularemos a derivada elemento por elemento. Isso nos permite dividir o cálculo do gradiente de erro entre os threads. Do curso de matemática da escola, sabemos que a derivada do logaritmo é igual à razão de 1 para o argumento da função. Assim, a derivada de nossa função de perda terá a seguinte forma.

Nós apenas temos que implementar a fórmula matemática acima no kernel do programa OpenCL. Seu código é bastante simples e cabe nas 2 linhas abaixo.

__kernel void SoftMax_OutputGradient(__global float* outputs,
                                     __global float* targets,
                                     __global float* output_gr)
  {
   size_t i = get_global_id(0);
   output_gr[i] = -targets[i] / (outputs[i] + 1e-37f);
  }

Assim concluímos o trabalho do lado do programa OpenCL e procedemos ao trabalho do lado do programa principal. Aqui adicionamos constantes para trabalhar com novos kernels, adicionamos uma declaração de novos kernels e criamos métodos para chamá-los.

#define def_k_SoftMax_FeedForward         36
#define def_k_softmaxff_inputs            0
#define def_k_softmaxff_outputs           1
#define def_k_softmaxff_total             2
//---
#define def_k_SoftMax_HiddenGradient      37
#define def_k_softmaxhg_outputs           0
#define def_k_softmaxhg_output_gr         1
#define def_k_softmaxhg_input_gr          2
//---
#define def_k_SoftMax_OutputGradient      38
#define def_k_softmaxog_outputs           0
#define def_k_softmaxog_targets           1
#define def_k_softmaxog_output_gr         2

Os métodos para chamar kernels repetem completamente os algoritmos usados anteriormente de métodos semelhantes. E seu código completo pode ser encontrado no anexo.

Depois de implementar a função SoftMax ausente, podemos começar a preparar um Expert Advisor para gerar e treinar o modelo de gradiente de política.

3.2 Criando o EA para treinar o modelo

Para treinar o modelo de aproximação da função de política de comportamento do agente, criaremos um novo Expert Advisor no arquivo "REINFORCE.mq5". A principal funcionalidade deste EA será emprestada do "Q-learning.mq5", que criamos no último artigo para treinar o modelo DQN. É importante notar que, ao contrário do modelo DQN, no novo Expert Advisor usamos apenas uma rede neural. Mas para a implementação correta do algoritmo, precisamos criar três pilhas: estados do ambiente, ações realizadas e recompensas recebidas.

CNet                StudyNet;
CArrayObj           States;
vectorf             vActions;
vectorf             vRewards;

Em seguida, alteramos ligeiramente os parâmetros externos do EA de acordo com os requisitos do algoritmo.

input int                  SesionSize =  24 * 22;
input int                  Iterations = 1000;
input double               DiscountFactor =   0.999;

O método de inicialização do Expert Advisor permaneceu praticamente inalterado. Acabamos de adicionar a inicialização da pilha para acumular ações realizadas e recompensas recebidas.

   if(!vActions.Resize(SesionSize) ||
      !vRewards.Resize(SesionSize))
      return INIT_FAILED;

O próprio processo de aprendizado é construído na função Train. Proponho analisá-lo com mais detalhes.

No início da função, como antes, determinamos o intervalo da amostra de treinamento de acordo com os parâmetros externos fornecidos.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

Após determinar o período de treinamento, carregamos a amostra de treinamento.

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();
//---
   int total = bars - (int)(HistoryBars + 2 * SesionSize);

As operações acima não diferem daquelas usadas em Expert Advisors anteriores. Isto é seguido por um sistema de laços de treinamento do modelo. Tal sistema utiliza as principais formas de treinar o modelo.

O loop externo é responsável por iterar as sessões de treinamento do modelo. E no início do laço, determinamos aleatoriamente a barra do início da sessão no pool geral do histórico carregado.

   CBufferFloat* State;
   for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++)
     {
      int error_code;
      int shift = (int)(fmin(fabs(Math::MathRandomNormal(0,1,error_code)),1) * (total) + SesionSize);
      States.Clear();

Em seguida, fazemos um laço em que nosso agente, passo a passo, percorre completamente a sessão. No corpo do loop, primeiro preenchemos o buffer do estado atual do sistema com dados históricos do período analisado. Realizamos uma operação semelhante ao treinar modelos anteriores antes de cada propagação.

      for(int batch = 0; batch < SesionSize; batch++)
        {
         int i = shift - batch;
         State = new CBufferFloat();
         if(!State)
           {
            ExpertRemove();
            return;
           }
         int r = i + (int)HistoryBars;
         if(r > bars)
            continue;
         for(int b = 0; b < (int)HistoryBars; b++)
           {
            int bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) ||
               !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) ||
               !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign))
               break;
           }

E realizamos uma propagação do nosso modelo.

         if(IsStopped())
           {
            ExpertRemove();
            return;
           }
         if(State.Total() < (int)HistoryBars * 12)
            continue;
         if(!StudyNet.feedForward(GetPointer(State), 12, true))
           {
            ExpertRemove();
            return;
           }

Com base nos resultados da propagação, obtemos uma distribuição de probabilidade de ações e amostramos a próxima ação da distribuição normal, levando em consideração a distribuição de probabilidade resultante. A amostragem é realizada por uma função separada, GetAction, cujos parâmetros recebem a distribuição de probabilidade.

         StudyNet.getResults(TempData);
         int action = GetAction(TempData);
         if(action < 0)
           {
            ExpertRemove();
            return;
           }

Após a amostragem da ação, determinamos a recompensa para a ação selecionada com base no tamanho da próxima vela. Utilizamos a política de remuneração adotada no último artigo.

         double reward = Rates[i - 1].close - Rates[i - 1].open;
         switch(action)
           {
            case 0:
               if(reward < 0)
                  reward *= -2;
               break;
            case 1:
               if(reward > 0)
                  reward *= -2;
               else
                  reward *= -1;
               break;
            default:
               reward = -fabs(reward);
               break;
           }

E armazenamos todo o conjunto de dados na pilha. Aqui é importante dizer que simplesmente adicionamos estados e ações às pilhas. Enquanto guardamos as recompensas, levando em consideração o fator de desconto. E aqui é necessário determinar na fase de projeto como iremos descontar as recompensas. São 2 variantes de desconto. Podemos descontar as recompensas iniciais dando mais valor às recompensas posteriores. Essa abordagem é mais usada quando o agente recebe recompensas intermediárias no processo de passagem pela sessão. Porém, a principal tarefa do agente é chegar ao final da sessão, onde ele receberá a recompensa máxima.

A segunda abordagem é a inversa, nela é dado mais peso às primeiras recompensas. E as recompensas subsequentes são descontadas. Esta variante é aceitável quando buscamos a recompensa máxima e mais rápida. Esta é exatamente a abordagem que eu usei. Afinal, é importante para nós obter imediatamente o lucro máximo e não ficar recebendo perdas à espera de uma reversão do mercado após uma transação.

Eis aqui outro ponto importante. Depois de completar a passagem pela sessão, temos que calcular a recompensa cumulativa de cada estado até o final da sessão. As operações vetoriais MQL5 permitem calcular apenas a soma cumulativa direta. Portanto, simplesmente armazenaremos todos os valores de recompensa em um vetor na ordem inversa. E depois que o loop termina, usamos uma operação vetorial para calcular a soma cumulativa.

         if(!States.Add(State))
           {
            ExpertRemove();
            return;
           }
         vActions[batch] = (float)action;
         vRewards[SessionSize - batch - 1] = (float)(reward * pow(DiscountFactor, (double)batch));
         vProbs[SessionSize - batch - 1] = TempData.At(action);
         //---
        }

Depois de salvar os dados, passamos para a próxima iteração do loop. Assim, coletamos dados para toda a sessão.

Após a conclusão de todas as iterações do laço, calcularemos a recompensa total da sessão, levando em consideração o desconto, o vetor de valores de recompensa acumulados de cada estado até o final da sessão e o valor da função de perda.

Aqui vamos salvar o modelo atual, mas somente se a recompensa máxima for atualizada.

      float cum_reward = vRewards.Sum();
      vRewards = vRewards.CumSum();
      vRewards = vRewards / fmax(vRewards.Max(), fabs(vRewards.Min()));
      float loss = (vRewards * MathLog(vProbs) * (-1)).Sum();
      if(MaxProfit < cum_reward)
        {
         if(!StudyNet.Save(FileName + ".nnw", loss, 0, 0, Rates[shift - SessionSize].time, false))
            return;
         MaxProfit = cum_reward;
        }

Agora que temos os valores das recompensas ao longo do caminho da sessão do agente, podemos realizar um loop de treinamento para o modelo de função de política. Para isso, preparamos mais um laço. Nele, vamos extrair alternadamente os estados do ambiente de nosso buffer e realizar uma propagação do modelo. Isso é necessário a fim de restaurar todos os valores internos do modelo para o estado correspondente do ambiente.

Em seguida, preparamos um vetor de valores de referência para o estado atual do ambiente. Lembre que vamos maximizar as probabilidades de escolher uma ação com recompensa positiva e minimizar as probabilidades de outras. Portanto, se durante a execução da ação recebemos um valor positivo, preenchemos o vetor de probabilidades de referência com valores zero. E apenas para a ação concluída, definimos a probabilidade como 1. No caso de receber uma recompensa negativa, preencheremos o vetor de probabilidades de referência com uns. E apenas para a ação selecionada, definimos a probabilidade como zero.

      for(int batch = 0; batch < SessionSize; batch++)
        {
         State = States.At(batch);
         if(!StudyNet.feedForward(State))
           {
            ExpertRemove();
            return;
           }
         if((vRewards[SessionSize - batch - 1] >= 0 ?
             (!TempData.BufferInit(Actions, 0) || !TempData.Update((int)vActions[batch], 1)) :
             (!TempData.BufferInit(Actions, 1) || !TempData.Update((int)vActions[batch], 0))
            ))
           {
            ExpertRemove();
            return;
           }
         if(!StudyNet.backProp(TempData))
           {
            ExpertRemove();
            return;
           }
        }

E faremos uma retropropagação para atualizar os coeficientes de peso do nosso modelo. As iterações são repetidas para todos os estados de ambiente salvos.

Depois de concluir todas as iterações do loop, enviamos uma mensagem informativa para o log e avançamos para a próxima sessão.

      PrintFormat("Iteration %d, Cummulative reward %.5f, loss %.5f", iter, cum_reward, loss);
     }
   Comment("");
//---
   ExpertRemove();
  }

Não se esqueça de controlar o processo de execução das operações em cada etapa. E após a execução bem-sucedida de todas as iterações, saímos da função e geramos um evento de fechamento de terminal. O código completo do EA pode ser encontrado no anexo.

Também é importante dizer que para aproximar a função de política do nosso modelo, usamos uma rede neural com uma arquitetura semelhante ao aprendizado da função Q do artigo anterior. Além disso, pegamos o modelo treinado do último artigo e substituímos o bloco de decisão nele e adicionamos SoftMax como a última camada da rede neural para normalizar os dados.

O processo de treinamento de um modelo é completamente semelhante ao processo de treinamento de qualquer outro modelo. Há muitos desses exemplos em cada artigo desta série. E para resumir o trabalho deste artigo, decidi me desviar um pouco do formato já modelo do artigo. Em vez disso, sugiro examinar o trabalho dos modelos treinados no testador de estratégia.

4. Prova do modelo treinado no testador de estratégia

No artigo anterior, treinamos um modelo DQN. Neste, criamos e treinamos um modelo de gradiente de política. E proponho criar EAs de teste e usá-los para ver o trabalho dos modelos no testador de estratégia. Para fazer isso, criaremos 2 Expert Advisors, "Q-learning-test.mq5" e "REINFORCE-test.mq5". Pelo nome dos arquivos, é fácil adivinhar qual modelo cada Expert Advisor está testando.

A estrutura de construção dos EAs é absolutamente a mesma. Portanto, vamos considerar apenas um. E o código completo de ambos os EAs pode ser encontrado no anexo.

O novo Expert Advisor "REINFORCE-test.mq5" é baseado no Expert Advisor "REINFORCE.mq5" discutido acima. Mas como o EA não treinará o modelo, removemos a função Train. Ao mesmo tempo, transferiremos a funcionalidade principal para a função OnTick, que processa cada evento de surgimento de novo tick.

Nosso modelo treinado avalia o estado do ambiente com base nas velas fechadas. Portanto, no corpo da função OnTick, verificamos a abertura de uma nova nova vela. E somente quando uma nova vela aparecer, as demais operações da função serão executadas.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
   if(lastBar >= iTime(Symb.Name(), TimeFrame, 0))
      return;

Quando uma nova vela aparece, carregamos os dados históricos mais recentes e preenchemos o buffer de descrição do estado do sistema.

   int bars = CopyRates(Symb.Name(), TimeFrame, 0, HistoryBars+1, Rates);
   if(!ArraySetAsSeries(Rates, true))
      return;
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();
//---
   State1.Clear();
   for(int b = 0; b < (int)HistoryBars; b++)
     {
      int bar_t = (int)HistoryBars - b;
      float open = (float)Rates[bar_t].open;
      TimeToStruct(Rates[bar_t].time, sTime);
      float rsi = (float)RSI.Main(bar_t);
      float cci = (float)CCI.Main(bar_t);
      float atr = (float)ATR.Main(bar_t);
      float macd = (float)MACD.Main(bar_t);
      float sign = (float)MACD.Signal(bar_t);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) ||
         !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
         !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
         !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
         break;
     }

Em seguida, verificamos se os dados foram preenchidos corretamente e chamamos uma propagação em nosso modelo.

   if(State1.Total() < (int)(HistoryBars * 12))
      return;
   if(!StudyNet.feedForward(GetPointer(State1), 12, true))
      return;
   StudyNet.getResults(TempData);
   if(!TempData)
     return;

Como resultado da propagação, obtemos uma distribuição de probabilidade de ações possíveis, da qual amostramos uma ação aleatória.

   lastBar = Rates[0].time;
   int action = GetAction(TempData);
   delete TempData;

Em seguida, temos que executar a ação selecionada. Mas antes de passar para a abertura de um novo negócio, verificaremos a disponibilidade de posições já abertas. Para fazer isso, definiremos 2 sinalizadores: Buy e Sell. Ao declarar variáveis, nós as definimos como false.

Depois disso, fazemos um loop com a iteração de todos os valores. E ao encontrar uma posição aberta para o símbolo analisado, mudaremos o valor do sinalizador correspondente.

   bool Buy = false;
   bool Sell = false;
   for(int i = 0; i < PositionsTotal(); i++)
     {
      if(PositionGetSymbol(i) != Symb.Name())
         continue;
      switch((ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE))
        {
         case POSITION_TYPE_BUY:
            Buy = true;
            break;
         case POSITION_TYPE_SELL:
            Sell = true;
            break;
        }
     }

Em seguida vem o bloco de operações de negociação. Aqui usamos a instrução switch para ramificar o algoritmo do bloco, dependendo da ação que está sendo executada. Se a escolha recaiu sobre a abertura de uma nova posição, verificamos os sinalizadores das posições abertas. No caso de uma posição já ter sido aberta na direção correspondente, simplesmente a deixamos no mercado e aguardamos a abertura de uma nova vela.

Se, no momento da tomada de decisão, estiver aberta uma posição oposta, primeiro fechamos a posição aberta e só depois abrimos uma nova.

   switch(action)
     {
      case 0:
         if(!Buy)
           {
            if((Sell && !Trade.PositionClose(Symb.Name())) ||
               !Trade.Buy(Symb.LotsMin(), Symb.Name()))
              {
               lastBar = 0;
               return;
              }
           }
         break;
      case 1:
         if(!Sell)
           {
            if((Buy && !Trade.PositionClose(Symb.Name())) ||
               !Trade.Sell(Symb.LotsMin(), Symb.Name()))
              {
               lastBar = 0;
               return;
              }
           }
         break;
      case 2:
         if(Buy || Sell)
            if(!Trade.PositionClose(Symb.Name()))
              {
               lastBar = 0;
               return;
              }
         break;
     }
//---
  }

Caso o agente precise fechar todas as posições, então chamamos a função de fechamento de posições para o símbolo atual. A função é chamada apenas se pelo menos uma posição estiver aberta.

E, claro, não esquecemos de controlar o processo de execução das operações em cada etapa.

O código completo do EA pode ser encontrado no anexo.

Testamos primeiro o modelo DQN. E aqui recebemos uma surpresa. O modelo deu lucro. Mas, ao mesmo tempo, ela fez apenas uma operação de negociação, que ficou aberta durante todo o teste. O gráfico do instrumento com um negócio perfeito é mostrado abaixo.

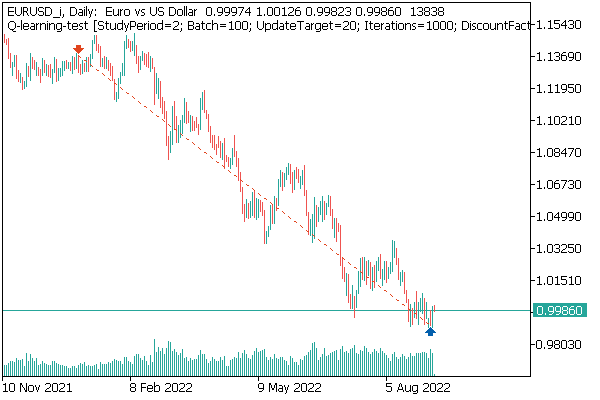
Ao avaliar esse negócio no gráfico do instrumento, não se pode deixar de concordar que o modelo identificou claramente a tendência global e abriu um negócio em sua direção. O negócio é lucrativo, mas fica a dúvida: será que o modelo conseguirá fechar tal negócio a tempo? Na verdade, treinamos o modelo com dados históricos dos últimos 2 anos. E, durante todos os 2 anos, o mercado foi dominado por uma tendência de baixa para o instrumento analisado. Portanto, surge a dúvida de se o modelo conseguirá fechar o negócio a tempo.

E aqui é importante dizer que ao usar a estratégia gananciosa, o modelo de gradiente de política dá resultados semelhantes. E lembre que, quando começamos a estudar métodos de aprendizado por reforço, enfatizei repetidamente a necessidade da escolha certa da política de recompensa. E então decidi experimentar a política de recompensa. Em particular, para excluir o fato de permanecer muito tempo em uma posição de perda, decidi aumentar as penalidades para posições não lucrativas. E, consequentemente, treinei o modelo de gradiente de política levando em consideração a nova política de recompensa. Depois de vários experimentos com os hiperparâmetros do modelo, consegui atingir 60% de lucratividade nas operações. O gráfico de testes é mostrado abaixo.

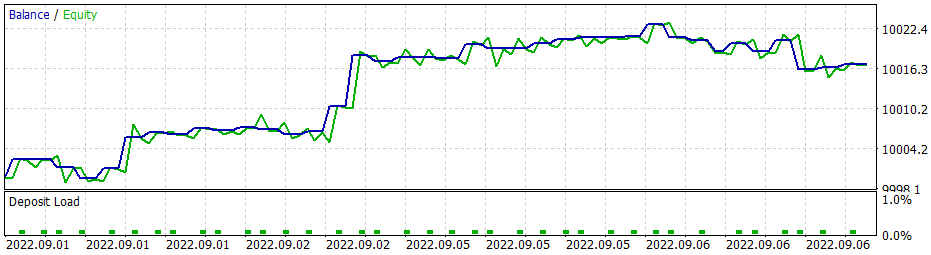
O tempo médio de manutenção da posição é de 1 hora e 40 minutos.

Considerações finais

Neste artigo, estudamos outro algoritmo proveniente dos métodos de aprendizado por reforço. Criamos e treinamos um modelo usando o método de gradiente de política.

Ao contrário de outros artigos desta série, neste treinamos e testamos os modelos com ajuda do testador de estratégia. Olhando para os resultados do teste, podemos concluir que os modelos são bastante capazes de gerar sinais para tornar as operações de negociação lucrativas. Ao mesmo tempo, vale ressaltar mais uma vez a importância de escolher a política de recompensa e a função de perda corretas para atingir o resultado desejado.

Referências

1. Redes neurais de maneira fácil (Parte 25): exercícios práticos de transferência de aprendizado
2. Redes neurais de maneira fácil (Parte 26): aprendizado por reforço
3. Redes neurais de maneira fácil (Parte 27): aprendizado Q profundo (DQN)

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	REINFORCE.mq5	EA	EA para treinamento de modelos
2	REINFORCE-test.mq5	EA	EA para prova do modelo no testador de estratégia
1	Q-learning-test.mq5	EA	Expert Advisor para provar o modelo DQN no testador de estratégia
2	NeuroNet.mqh	Biblioteca de classes	Biblioteca para preparar modelos de redes neurais
3	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL para preparar modelos de redes neurais

…