를 포함하는 두 평행선 사이의 거리를 계산하십시오.
여기요!
그리고 어떻게 그러한 좌표계를 구축할 수 있습니까? 어떻게 상상하십니까?
X 축을 따라 한 지점에서 거리를 측정해야합니다. 이것은 당신의 시간입니다, 나는 추측합니다 ...
아니면 오프셋으로 측정해야 합니까? 그런 다음 피타고라스 정리에 의해 두 변과 한 각이 알려져 있습니다 ...
그러나 거리가 무엇인지에 따라 - 픽셀 단위로? 그런 다음 처음에는 모든 것을 적절한 좌표계로 변환해야 합니다.논리적으로 생각한다면 빨간 선은 거리를 측정하기 위해 이 두 개의 (검은색) 선에 수직이어야 합니다. 이 값이 얼마로 측정되는지는 중요하지 않습니다. 저에게 가장 중요한 것은 눈금이 변경될 때 이 값이 변경되지 않는다는 것입니다.
나는 이것을 시도했습니다 : 선의 교차점 값을 취하고 그 사이 의 막대 수를 계산하십시오 ... 이 접근 방식은 눈금을 변경할 때 적합하지 않습니다!
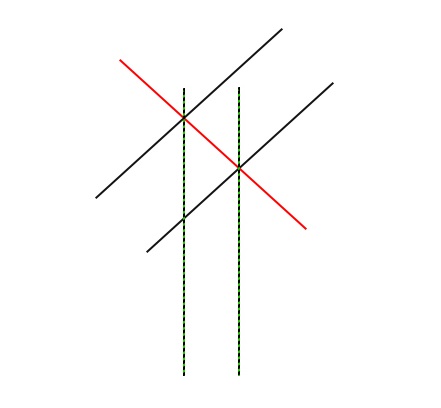
스케일이 영향을 미치지 않도록 고정 차트 스케일을 사용해야 합니다. 그렇지 않으면 항상 영향을 미칩니다.
왜요 ? 그러나 비율은 어떻습니까?
Itum :
이 값이 얼마로 측정되는지는 중요하지 않습니다. 저에게 가장 중요한 것은 눈금이 변경될 때 이 값이 변경되지 않는다는 것입니다.
음, 그렇다면 일반적으로 간단합니다. 포인트로 측정합니다. 두 라인은 가격에 묶여 있으며 눈금이 변경될 때 두 라인 사이의 거리는 변경되지 않고 라인의 시각적 표시만 변경됩니다.
여기에서 스케일이 다른 스크린샷에서 선을 확인했습니다. 보시다시피 선 사이의 거리는 변경되지 않습니다.
귀하의 경우 문제는 점 사이의 거리 개념이 "가격 / 초"공간에 정의되어 있지 않다는 것입니다. 따라서 최단 거리를 찾는 것은 불가능합니다.
축의 치수가 다르기 때문입니다. 따라서 다음 중 하나가 필요합니다.
- 가격과 시간 사이의 X 요소를 선택하면 거리는 ( 가격 x 초 x X )의 제곱근 단위입니다.
- 한 축을 따라 거리를 계산합니다.
수직 거리는 차트의 기간이 변경되어도 실제로 변경되지 않습니다(불완전한 막대와 휴무일이 있기 때문에).
수평 거리는 전혀 변하지 않습니다.
그러나 한 축을 따라 거리를 측정할 때는 무한할 수 있으며 이는 의미가 없습니다.
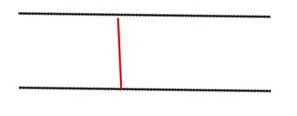
그래프의 눈금을 포함하여 두 평행선 사이의 거리를 계산하는 방법을 알려주세요(눈금에 영향을 주지 않도록)
다음은 예입니다.
빨간색 선은 두 평행선 사이의 거리입니다. 어떻게 계산합니까?
모든 것은 기본이야, 왓슨...
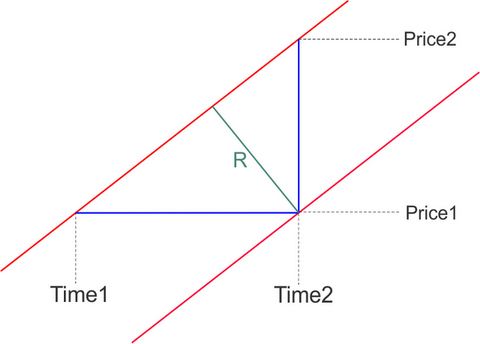
2차원 가격 X 시간 시스템을 가격 X 가격 평면으로 축소하기 위해서는 보다 논리적으로 가격 변화율 V라고 하는 새로운 특성을 도입할 필요가 있습니다.
그리고 포인트/초 단위로 측정하는 것이 편리합니다.
또한, V = 이것에 정비례하는 시스템에서 선 각도의 탄젠트:
- 1 수직 픽셀 = 1 _Point
- 가로 1픽셀 = 1초(화면에서 60픽셀 너비의 1분 막대)
그런 다음 두 평행선의 거리는 두 가지 방법으로 계산할 수 있습니다.
double V=(Price2-Price1)/(Time2-Time1); ulong DeltaTime = TimeLine2-TimeLine1; // double DeltaPrice = PriceLine2- PriceLine1; double R=DeltaTime*V/ sqrt ( 1 +V*V) ; // double R=V/(DeltaPrice*sqrt(1+V*V)) ; // где // точки (Price1,Time1) и (Price2,Time2) это две любые точки лежащие на одной из параллельных линий, Time измеряется в секундах // TimeLine1 и TimeLine2 - время первой и второй линии при фиксированной цене (пересечение с горизонтальной линией) // PriceLine1 и PriceLine2- цена первой и второй линии при фиксированном времени (пересечение с вертикальной линией) // DeltaPrice - расстояние между линиями в пунктах по вертикали // DeltaTime - расстояние между линиями в секундах по горизонтали // R - искомое кратчайшее расстояние между двумя параллельными линиями, скорость измерения цены которых равна V пунктов в секунду
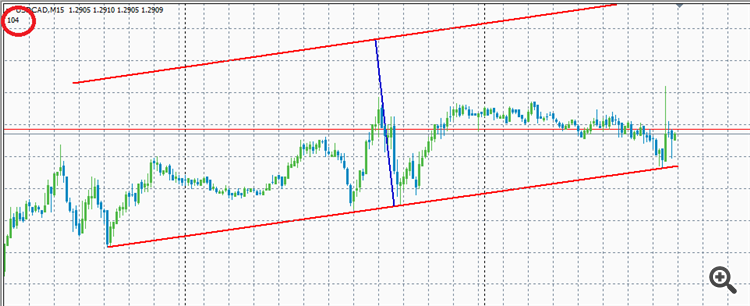
이 수직선은 위 시스템의 비율과 다른 비율을 가진 시스템에서 수직선처럼 보이지 않을 것이 분명합니다.
모든 것은 기본이야, 왓슨...
2차원 가격 X 시간 시스템을 가격 X 가격 평면으로 축소하기 위해서는 보다 논리적으로 가격 변화율 V라고 하는 새로운 특성을 도입할 필요가 있습니다.
그리고 포인트/초 단위로 측정하는 것이 편리합니다.
또한, V = 이것에 정비례하는 시스템에서 선 각도의 탄젠트:
- 1 수직 픽셀 = 1 _Point
- 가로 1픽셀 = 1초(화면에서 60픽셀 너비의 1분 막대)
그런 다음 두 평행선의 거리는 두 가지 방법으로 계산할 수 있습니다.
이 수직선은 위 시스템의 비율과 다른 비율을 가진 시스템에서 수직선처럼 보이지 않을 것이 분명합니다.
Time1=TimeLine1, Time2=TimeLine2인 경우가 있기 때문에 단순화할 수 있습니다.
그 다음에:
double V=(Price2-Price1)/(Time2-Time1); double R=(Price2-Price1)/ sqrt ( 1 +V*V) ;
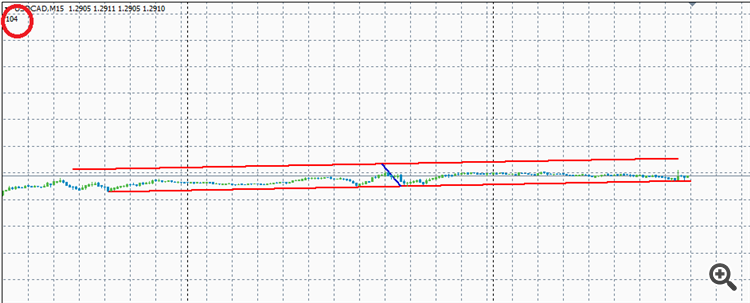
그래프의 눈금을 포함하여 두 평행선 사이의 거리를 계산하는 방법을 알려주세요(눈금에 영향을 주지 않도록)
다음은 예입니다.
빨간색 선은 두 평행선 사이의 거리입니다. 어떻게 계산합니까?