링크 주셔서 감사합니다. 관련 아이디어를 찾고 있었습니다. R 기능의 관점에서 질문에 접근할 필요가 없다고 생각합니다. 기존 접근 방식:
측정 단위(숫자, 방향, 거리)의 의미 손실을 무시하고 중심 좌표가 Xc, Yc인 반지름이 R인 원의 방정식에서 직접
R^2 = (X-Xc)^2 + (Y-Yc)^2
숫자 i(Xi = i)가 있는 점에서 잔차 함수를 만듭니다. 이것은 점(Xi, Yi)에서 중심 Xc, Yc까지의 거리와 반지름 R 사이의 차이입니다.
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
우리는 제곱 Di를 더하고 목적 함수가 최소화되도록 합니다. R, Xc, Yc의 세 가지 필수 변수 매개변수가 있습니다. 극단 (첫 번째 및 마지막) 점은 중간 점 (인접 점 없음)보다 영향이 적으므로 해당 Di ^ 2에 2를 곱하는 것이 좋습니다. 그리고 마지막 포인트에 중점을 두고 피팅하기 위해 가중치에 대해 다른 열을 추가하여 마지막 몇 포인트의 가중치로 재생할 수도 있습니다.
비뚤어지면 측정 단위를 고려해야합니다. 거리를 계산할 때 X와 Y의 영향이 거의 같게 하려면(R은 두 가지 영향을 모두 받습니다), X에 대해 숫자 i가 아니라 동일한 숫자에 평준화 척도를 곱한 값을 취해야 합니다. X와 Y의 범위는 크기가 비슷합니다.
추신 sernam.ru는 저작권 침해 혐의를 매우 교활하게 제거하여 책의 텍스트를 부분적으로만 출판하고 인쇄물, 특히 책 제목을 지정하지 않은 것으로 나타났습니다. sernam.ru에서는 인터넷 어디에서도 찾을 수 없는 텍스트를 찾을 수 있습니다.
시간 내 주셔서 감사합니다...
공식 Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R에 따라 최소화할 필요가 있음을 깨달았습니다.
그런 다음 플레이어에서 찾을 수 있는 원을 만들어야 합니다. 방정식은 ...
y=(R^2-(X-Xc)^2)^0.5+Yc
블라디미르 :
하나 더. 호와 다항식 모두에 대해 Excel에서 회귀를 시도했습니다. 결과는 크게 다르지 않습니다. 그래서 이것에 시간을 낭비하지 마십시오. 틱과 같은 직선 대신 호를 기반으로 표시기를 만들 수 있지만. 아마도 sma보다 더 잘 작동할 것입니다.
블라디미르 :
여기 내가 사용한 공식이 있습니다.
일반 호 방정식: (x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , 여기서 R에 대한 공식은 그림에 나와 있습니다.
그러나 이것은 포지티브 평면에만 적합합니다. 실험을 위해 나는 긍정적 인 평면에있는 "호를 따라 가격 채널"을 가져갔습니다.
그건 그렇고, 모니터링 사이트에서 수익성 측면의 리더는 이제 "다항식"이라는 이름의 계정입니다. 그 결과 보증금이 660배 증가합니다. 이것은 광고를 위한 것이 아닙니다(광고할 수 없습니다. 소유자는 오스트리아에서 온 소녀입니다). 이것은 아마도 당신이 올바른 길을 찾는 데 도움을 주기 위한 것입니다.
나는 여기에서 다항식, 최소 제곱, 다양한 근사 방법, 예측 가능성 등에 대한 논쟁을 읽었습니다. ... 누군가는 예측을 믿고 누군가는 믿지 않습니다. 그러나 내가 찾길 바랐던 것은 보지 못했습니다. 내가 의미하는 바를 설명하기 위해 나는 우주의 중력에 대한 비유를 사용할 것입니다. 내가 만든 애니메이션 gif를 살펴보자. 자신의 질문에 답하십시오. 각 물체의 궤적을 예측할 수 있습니까? 물론 할 수 있습니다. 그러나 현재 각 물체에 대한 정보를 알고 있는 경우에만 질량, 현재 위치 및 이동 방향, 물체가 나타난 시간 및 사라진 시간. 그리고 본질적으로 하나의 공식만 사용하는 수학 및 계산 문제입니다(빛의 속도에서 멀리 떨어진 속도에 대한 고전 역학의 변형에 대해).
또한 우리 행성도 악순환이 아니라 3차원 정현파(나선형)로 움직인다는 것을 이해해야 합니다.
이 비디오는 그것을 명확하게 보여줍니다:
하지만 모든 객체에 대한 정보가 없다면 어떻게 될까요? 과거의 궤적 자체만 알고도 궤적을 예측할 수 있을까? 여기서부터 재미가 시작됩니다.
누군가가 아니오라고 말하면 불가능합니다. 대답은 정확하지 않습니다. 긍정적인 대답도 잘못된 것입니다. 이 문제에 대한 해결책은 확률적일 뿐입니다. 문제는 반대로 해결해야 합니다. 이전 궤적을 기반으로 먼저 물체의 주요 "덩어리"와 질량의 확률적 궤적을 계산해야 합니다. 그런 다음 가능한 궤적의 확률 모델을 예측합니다. 이것이 AI의 기본 작업인 패턴 인식입니다. 내가 이해하는 바는 Maxim Dmitrievsky가 말한 내용이었습니다. 약 6년 전에 저는 이 분야의 첫 번째 개발을 KB( https://www.mql5.com/ru/code/10882 )에 게시했습니다. 나는 거기에 있는 채널을 인식하기 위해 1도의 다항식(선형 회귀)을 사용했습니다. 그 이후로 저는 이 분야에서 상당한 진전을 이루었습니다. 그러나 나는 어떤 것도 공개하지 않으며 명백한 이유로 공개하지 않을 것입니다. 궁금하신 분들을 위해 힌트를 드릴 뿐입니다. 선형 채널을 찾는 것은 본질적으로 이러한 중력 질량의 중심을 찾는 것입니다. 그리고 원칙적으로 모든 악기 (기호)에는 5 ~ 10 개의 센터 (채널)가 있습니다. 가격을 예측하려면 이 모든 것을 동시에 고려해야 합니다. 이 경우에만 예측의 정확성이 50%를 크게 초과합니다. 그럼에도 불구하고 그들은 특별한 숫자 집합을 찾으려고 노력하며 미래를 예측할 것이라고 순진하게 믿습니다. 사실 이 "숫자 집합"은 살아 있고 역동적이며 물질 중력과 유사하게 많은 물체의 국소 질량 중심 위치가 변하는 것처럼 끊임없이 변하고 있습니다. 그리고 과제는 이 "숫자 집합"의 변화 법칙을 찾고 심지어 법칙 자체의 변화 법칙을 찾는 것으로 귀결됩니다. :)) 이상적으로는 이 "숫자 집합"을 매 틱마다 다시 계산해야 합니다. 이것이 바로 제가 많은 사람들이 최적화라고 부르는 특정 "숫자 집합"을 찾는 것이 과거 데이터에 대한 진부한 적합성이라고 반복해서 말한 이유입니다.
중력에 대한 비유가 매우 적절하다고 생각합니다. 돈은 시장에서 중력을 만듭니다. 누군가는 100달러로, 누군가는 수십억으로 들어갈 것입니다. 동일한 중력 법칙이 여기에서 작동하며 심지어 위에서 설명한 것과 동일한 공식이 적용됩니다. 끌어당기는 힘은 거리의 제곱에 반비례하고 질량에 정비례합니다. 따라서 2차 다항식 회귀(포물선)가 가장 적합한 도구입니다. 쌍곡선을 사용하는 것이 더 논리적이지만 두 중력체의 상호 작용이 발생하는 것은 쌍곡선의 법칙에 정확히 따르기 때문입니다. 그러나 사실은 포물선이 계산에 훨씬 더 편리할 뿐만 아니라 가장 중요한 구간에서 포물선과 쌍곡선이 매우 유사하다는 것입니다. 여기 에서 분명히 볼 수 있습니다. 빨간색 선은 포물선, 파란색 선은 쌍곡선입니다.
돈의 중력과 천체의 중력의 주요 차이점은 돈이 갑자기 나타났다가 사라지면서 강력한 중력 변동을 일으킬 수 있다는 것입니다. 하지만 이 이벤트를 계산하기 위해서는 채널 고장과 같은 것이 있습니다.
링크 주셔서 감사합니다. 관련 아이디어를 찾고 있었습니다. R 기능의 관점에서 질문에 접근할 필요가 없다고 생각합니다. 기존 접근 방식:
측정 단위(숫자, 방향, 거리)의 의미 손실을 무시하고 중심 좌표가 Xc, Yc인 반지름이 R인 원의 방정식에서 직접
R^2 = (X-Xc)^2 + (Y-Yc)^2
숫자 i(Xi = i)가 있는 점에서 잔차 함수를 만듭니다. 이것은 점(Xi, Yi)에서 중심 Xc, Yc까지의 거리와 반지름 R 사이의 차이입니다.
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
우리는 제곱 Di를 더하고 목적 함수가 최소화되도록 합니다. R, Xc, Yc의 세 가지 필수 변수 매개변수가 있습니다. 극단 (첫 번째 및 마지막) 점은 중간 점 (인접 점 없음)보다 영향이 적으므로 해당 Di ^ 2에 2를 곱하는 것이 좋습니다. 그리고 마지막 포인트에 중점을 두고 피팅하기 위해 가중치에 대해 다른 열을 추가하여 마지막 몇 포인트의 가중치로 재생할 수도 있습니다.
비뚤어지면 측정 단위를 고려해야합니다. 거리를 계산할 때 X와 Y의 영향이 거의 같게 하려면(R은 두 가지 영향을 모두 받습니다), X에 대해 숫자 i가 아니라 동일한 숫자에 평준화 척도를 곱한 값을 취해야 합니다. X와 Y의 범위는 크기가 비슷합니다.
추신 sernam.ru는 저작권 침해 혐의를 매우 교활하게 제거하여 책의 텍스트를 부분적으로만 출판하고 인쇄물, 특히 책 제목을 지정하지 않은 것으로 나타났습니다. sernam.ru에서는 인터넷 어디에서도 찾을 수 없는 텍스트를 찾을 수 있습니다.
공식 Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R에 따라 최소화할 필요가 있음을 깨달았습니다.
그런 다음 플레이어에서 찾을 수 있는 원을 만들어야 합니다.
방정식은 ...
y=(R^2-(X-Xc)^2)^0.5+Yc
그래서 이것에 시간을 낭비하지 마십시오. 틱과 같은 직선 대신 호를 기반으로 표시기를 만들 수 있지만. 아마도 sma보다 더 잘 작동할 것입니다.
여기 내가 사용한 공식이 있습니다.
일반 호 방정식:
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , 여기서 R에 대한 공식은 그림에 나와 있습니다.
그러나 이것은 포지티브 평면에만 적합합니다. 실험을 위해 나는 긍정적 인 평면에있는 "호를 따라 가격 채널"을 가져갔습니다.
그냥 예쁜 이름일지도...
RRR5 :
...
그러나 이것은 포지티브 평면에만 적합합니다. 실험을 위해 나는 긍정적 인 평면에있는 "호를 따라 가격 채널"을 가져갔습니다.
"포지티브 플레인"이란 무엇입니까?
"포지티브 플레인"이란 무엇입니까?
그러나 이것을위한 것이 아닙니다.
글쎄, 그러한 호의 경우 작동 할 것입니다.
그러나 이것을위한 것이 아닙니다.
RRR5, 당신은 빨리 그림을 그립니다. 흥미로운 점은 무엇입니까?
나는 여기에서 다항식, 최소 제곱, 다양한 근사 방법, 예측 가능성 등에 대한 논쟁을 읽었습니다. ...
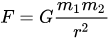
누군가는 예측을 믿고 누군가는 믿지 않습니다.
그러나 내가 찾길 바랐던 것은 보지 못했습니다.
내가 의미하는 바를 설명하기 위해 나는 우주의 중력에 대한 비유를 사용할 것입니다.
내가 만든 애니메이션 gif를 살펴보자.
자신의 질문에 답하십시오. 각 물체의 궤적을 예측할 수 있습니까?
물론 할 수 있습니다.
그러나 현재 각 물체에 대한 정보를 알고 있는 경우에만 질량, 현재 위치 및 이동 방향, 물체가 나타난 시간 및 사라진 시간.
그리고 본질적으로 하나의 공식만 사용하는 수학 및 계산 문제입니다(빛의 속도에서 멀리 떨어진 속도에 대한 고전 역학의 변형에 대해).
프로그램 자체는 여기서 끈적끈적한 중력입니다. 당신은 주위에 놀 수 있습니다.
또한 우리 행성도 악순환이 아니라 3차원 정현파(나선형)로 움직인다는 것을 이해해야 합니다.
이 비디오는 그것을 명확하게 보여줍니다:
하지만 모든 객체에 대한 정보가 없다면 어떻게 될까요?
과거의 궤적 자체만 알고도 궤적을 예측할 수 있을까?
여기서부터 재미가 시작됩니다.
누군가가 아니오라고 말하면 불가능합니다. 대답은 정확하지 않습니다. 긍정적인 대답도 잘못된 것입니다.
이 문제에 대한 해결책은 확률적일 뿐입니다.
문제는 반대로 해결해야 합니다. 이전 궤적을 기반으로 먼저 물체의 주요 "덩어리"와 질량의 확률적 궤적을 계산해야 합니다. 그런 다음 가능한 궤적의 확률 모델을 예측합니다.
이것이 AI의 기본 작업인 패턴 인식입니다.
내가 이해하는 바는 Maxim Dmitrievsky가 말한 내용이었습니다.
약 6년 전에 저는 이 분야의 첫 번째 개발을 KB( https://www.mql5.com/ru/code/10882 )에 게시했습니다. 나는 거기에 있는 채널을 인식하기 위해 1도의 다항식(선형 회귀)을 사용했습니다. 그 이후로 저는 이 분야에서 상당한 진전을 이루었습니다. 그러나 나는 어떤 것도 공개하지 않으며 명백한 이유로 공개하지 않을 것입니다. 궁금하신 분들을 위해 힌트를 드릴 뿐입니다.
선형 채널을 찾는 것은 본질적으로 이러한 중력 질량의 중심을 찾는 것입니다.
그리고 원칙적으로 모든 악기 (기호)에는 5 ~ 10 개의 센터 (채널)가 있습니다. 가격을 예측하려면 이 모든 것을 동시에 고려해야 합니다. 이 경우에만 예측의 정확성이 50%를 크게 초과합니다.
그럼에도 불구하고 그들은 특별한 숫자 집합을 찾으려고 노력하며 미래를 예측할 것이라고 순진하게 믿습니다.
사실 이 "숫자 집합"은 살아 있고 역동적이며 물질 중력과 유사하게 많은 물체의 국소 질량 중심 위치가 변하는 것처럼 끊임없이 변하고 있습니다. 그리고 과제는 이 "숫자 집합"의 변화 법칙을 찾고 심지어 법칙 자체의 변화 법칙을 찾는 것으로 귀결됩니다. :))
이상적으로는 이 "숫자 집합"을 매 틱마다 다시 계산해야 합니다. 이것이 바로 제가 많은 사람들이 최적화라고 부르는 특정 "숫자 집합"을 찾는 것이 과거 데이터에 대한 진부한 적합성이라고 반복해서 말한 이유입니다.
중력에 대한 비유가 매우 적절하다고 생각합니다. 돈은 시장에서 중력을 만듭니다. 누군가는 100달러로, 누군가는 수십억으로 들어갈 것입니다. 동일한 중력 법칙이 여기에서 작동하며 심지어 위에서 설명한 것과 동일한 공식이 적용됩니다. 끌어당기는 힘은 거리의 제곱에 반비례하고 질량에 정비례합니다. 따라서 2차 다항식 회귀(포물선)가 가장 적합한 도구입니다. 쌍곡선을 사용하는 것이 더 논리적이지만 두 중력체의 상호 작용이 발생하는 것은 쌍곡선의 법칙에 정확히 따르기 때문입니다. 그러나 사실은 포물선이 계산에 훨씬 더 편리할 뿐만 아니라 가장 중요한 구간에서 포물선과 쌍곡선이 매우 유사하다는 것입니다.
여기 에서 분명히 볼 수 있습니다. 빨간색 선은 포물선, 파란색 선은 쌍곡선입니다.
돈의 중력과 천체의 중력의 주요 차이점은 돈이 갑자기 나타났다가 사라지면서 강력한 중력 변동을 일으킬 수 있다는 것입니다. 하지만 이 이벤트를 계산하기 위해서는 채널 고장과 같은 것이 있습니다.
이 문제에 대한 해결책은 확률적일 뿐입니다.
문제는 반대로 해결해야 합니다. 이전 궤적을 기반으로 먼저 물체의 주요 "덩어리"와 질량의 확률적 궤적을 계산해야 합니다. 그런 다음 가능한 궤적의 확률적 모델을 예측합니다.
여기서 "확률적 해법"이 주어진 공간에서 모든 궤적의 전체 집합이 될까봐 두렵습니다. 이 해법의 가치는 무엇입니까?
올해 유로달러가 100을 넘지 않고 음수가 아닐 것이라는 "높은 확률로" 말하는 것과 같습니다. 이 진술의 확률은 100%에 가깝습니다. 그러나 그러한 "예측"에서 얼마나 많은 이점을 얻을 수 있습니까?
확률 이론에서는 많은 독립된 힘이 물체의 상태에 영향을 줄 때 상태의 확률이 가우스 법칙을 따르기 시작한다는 것을 증명합니다. 그러나 가격의 과정과 가치는 시장 참가자의 투입물과 산출물이 의존한다는 단순한 이유 때문에 이러한 분포의 대상이 아닙니다.
RRR5 :
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
그러나 이것은 포지티브 평면에만 적합합니다. 실험을 위해 나는 긍정적 인 평면에있는 "호를 따라 가격 채널"을 가져갔습니다.
왜 MNC를 좋아하지 않는지 이해가 되지 않습니다. 그는 결국 일반적으로 지정된 곡선을 만듭니다.
나는 작은 TF에서 일하는 것을 좋아하지만 그런 단점은 좋아하지 않습니다.
어떻게 예측할 수 있습니까?