불가능한 일이 가능한가?

새 코멘트
 

전능의 역설:

일반적으로 역설은 다음과 같은 질문으로 공식화됩니다. "신이 스스로 들 수 없는 돌을 만들 수 있습니까?" ( 예, 끝없는 생성 및 상승주기라고 생각합니다 ) 또는

" 신이 내각이 180도가 되지 않는 삼각형을 만들 수 있을까요 ?" ( 예, 리만 기하학이라고 생각합니다) .

콜럼버스가 "24시간 이내에 유럽에서 미국으로 갈 수 있습니까?"라는 질문을 받았다면 당시의 가능성을 염두에 두고 아니요라고 대답했을 것입니다. 하지만 오늘날에는 어떤 어린이도 가능하다고 말할 것입니다. . 이것은 "이 가능성이 콜럼버스 시대에 이미 존재했습니까, 아니면 우리 시대에만 나타났습니까?"라는 질문으로 이어집니다. 이론적으로 이 가능성은 항상 존재했지만 실제로는 우리 시대에만 가능하게 되었습니다. 이것으로부터 다음과 같은 결론을 내리는 것이 가능합니까? 우리가 물리적으로 구현할 수 있는지 여부에 관계없이 수학에 모순되지 않는 모든 것이 가능합니까? 기회는 우리가 알든 모르든 존재합니다.

Геометрия Римана — Википедия
  • ru.wikipedia.org
Геометрия Римана (Эллиптическая геометрия) — одна из трёх «великих геометрий» (Евклида, Лобачевского и Римана). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой гауссовой кривизной, Лобачевского — с постоянной отрицательной, то геометрия Римана реализуется на поверхностях с постоянной положительной гауссовой кривизной, т...
 
불가능은 이해하거나 제기하는 것이 불가능하지 않으며 아마도 신에게만 ... 또는 반신 ...
 

역설의 주제는 일반적으로 매우 흥미롭고 점차 선으로 이어지며 열린 마음으로 생각하도록 가르칩니다.

나는 행이 1-2 + 3-4 + 5 .. (숫자가 하나씩 차례로 변경됨) ..=> 1/4

여기에서 사랑받지 못하는 terver와 matstat에는 많은 역설이 있습니다 :-)

 
A. 아인슈타인은 씁니다. “공의 표면에 사는 완전히 납작한 딱정벌레를 상상해 보십시오. 이 딱정벌레는 분석 정신을 부여받을 수 있으며 물리학을 공부하고 책을 쓸 수도 있습니다. 그의 세계는 2차원적일 것이다. 정신적으로든 수학적으로든 그는 3차원이 무엇인지 이해할 수도 있지만 이 차원을 시각적으로 시각화할 수는 없습니다. 사람은 이 딱정벌레와 정확히 같은 위치에 있지만 사람이 3차원이라는 유일한 차이점이 있습니다.

수학적으로 사람은 4차원을 상상할 수 있지만 물리적으로 사람은 그것을 볼 수 없고 시각적으로 시각화합니다. 그에게 4차원은 수학적으로만 존재합니다. 그의 마음은 4차원을 이해할 수 없다”(A. Einstein. Collection of science works. Volume 4. M. Nauka, 1967).
 
Maxim Kuznetsov :

...

여기에서 사랑받지 못하는 terver와 matstat에는 많은 역설이 있습니다 :-)

왜 확률 이론과 수학 통계가 갑자기 여기에서 사랑받지 못하게 되었습니까? 여기에서는 모든 것이 괜찮은 것 같습니다. 여기에 확률 이론과 문제의 수학적 통계를 기반으로 한 말도 안되는 이야기가 있습니다.

역설이란 무엇입니까?

 
Alexander Voronkov :
A. 아인슈타인은 씁니다. “공의 표면에 사는 완전히 납작한 딱정벌레를 상상해 보십시오. 이 딱정벌레는 분석 정신을 부여받을 수 있으며 물리학을 공부하고 책을 쓸 수도 있습니다. 그의 세계는 2차원이 될 것입니다. 정신적으로든 수학적으로든 그는 3차원이 무엇인지 이해할 수도 있지만 이 차원을 시각적으로 시각화할 수는 없습니다. 사람은 이 딱정벌레와 정확히 같은 위치에 있지만 사람이 3차원이라는 유일한 차이점이 있습니다.

수학적으로 사람은 4차원을 상상할 수 있지만 물리적으로 사람은 그것을 볼 수 없고 시각적으로 시각화합니다. 그에게 4차원은 수학적으로만 존재합니다. 그의 마음은 4차원을 이해할 수 없다”(A. Einstein. Collection of science works. Volume 4. M. Nauka, 1967).

아인슈타인과 GR/SRT는 일반적으로 좋습니다.

"거대한 두꺼비가 0.97С의 상대 속도로 당신을 향해 날아갑니다. 두꺼비가 정확히 무엇인지 이해할 수 있습니까?"

 
Dmitry Fedoseev :

왜 확률 이론과 수학 통계가 갑자기 여기에서 사랑받지 못하게 되었습니까? 여기에서는 모든 것이 괜찮은 것 같습니다. 여기에 확률 이론과 문제의 수학적 통계를 기반으로 한 말도 안되는 이야기가 있습니다.

역설이란 무엇입니까?

여기에서 그들은 두 단위가 독립적이라는 점을 감안할 때 1 + 1 = 2라고 믿습니다.
 


:)
 

MT4에서 테스트 시간의 내림차순으로 Expert Advisor를 자동으로 테스트할 수 있습니까? 예를 들어, 2015.01.01에서 2015.12.31까지, 다음 단계는 2015.01.02에서 2015.12.31까지입니다.

옵티마이저를 사용하여 이 문제를 해결합니다.

 //+------------------------------------------------------------------+
// Внешние переменные 
input bool CheckEvery_Day= false ;
input bool TestEachYearSeparately= false ;
input int   DayOfYear_= 1 ;
input int   Year_= 2009 ;
// Эксперт функция тик
void OnTick ( void )
  {
   if (CheckEvery_Day)
     {
       if (TestEachYearSeparately)
         if (Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_) || Year()>Year_) return ; //тестировать каждый год отдельно
       else
         if (Year()<Year_ || (Year()<=Year_ && DayOfYear()<DayOfYear_)) return ;                 //тестировать весь период 
     }

// Ваш код 

  }
//+------------------------------------------------------------------+

기간 선택:

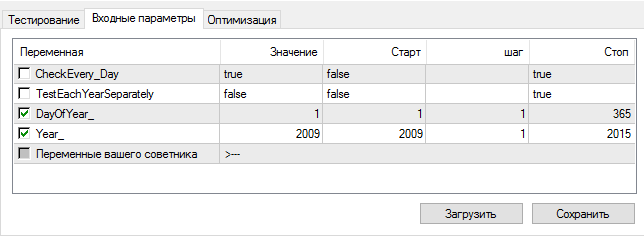
옵티마이저 활성화:

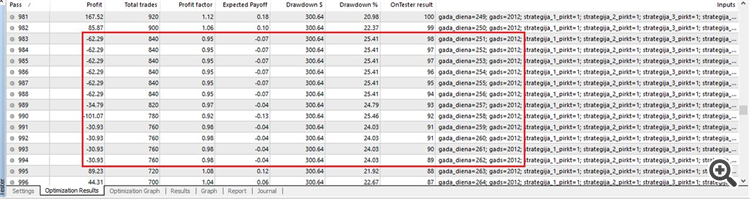
새로운 날부터 테스트를 시작할 때마다 EA가 테스트를 통과하는 방법을 확인할 수 있는 결과를 얻습니다.

 
Dmitry Fedoseev :

왜 확률 이론과 수학 통계가 갑자기 여기에서 사랑받지 못하게 되었습니까? 여기에서는 모든 것이 괜찮은 것 같습니다. 여기에 확률 이론과 문제의 수학적 통계를 기반으로 한 말도 안되는 이야기가 있습니다.

역설이란 무엇입니까?

TV와 MS의 역설은 처음 들어보셨나요?

여기 보세요. 여기에는 많은 좋은 예가 있습니다.

SEKEI G. / 확률 이론 및 수학 통계의 역설

범주: 수학 2010년 3월 11일

제목: 확률 이론과 수학 통계의 역설

저자: Sekey G.

초록: 헝가리 수학자의 책으로 확률 이론, 수학 통계 및 무작위 과정 이론에서 나온 예상치 못한 결론과 진술의 모음을 포함하고 있습니다. 이 책은 생동감 있고 흥미진진한 방식으로 작성되었으며 여기에 제시된 자료는 다음 그림에서 설명하는 데 사용할 수 있습니다. 확률 이론에 대한 대학 강의 및 일부 섹션 - 학교 학생들의 작업 수학 서클
다양한 자격을 갖춘 수학자 대상, 확률론 및 수리통계학 전공자 전원 대상

PDF로 다운로드(11.4MB): Sekei G. / 확률 이론 및 수학 통계의 역설

vixri.com

 
Олег avtomat :

TV와 MS의 역설은 처음 들어보셨나요?

여기 보세요. 여기에는 많은 좋은 예가 있습니다.

SEKEI G. / 확률 이론 및 수학 통계의 역설

범주: 수학 2010년 3월 11일

제목: 확률 이론과 수학 통계의 역설

저자: Sekey G.

초록: 헝가리 수학자의 책으로 확률 이론, 수학 통계 및 무작위 과정 이론에서 나온 예상치 못한 결론과 진술의 모음을 포함하고 있습니다. 이 책은 생동감 있고 흥미진진한 방식으로 작성되었으며 여기에 제시된 자료는 다음 그림에서 설명하는 데 사용할 수 있습니다. 확률 이론에 대한 대학 강의 및 일부 섹션 - 학교 학생들의 작업 수학 서클
다양한 자격을 갖춘 수학자 대상, 확률론 및 수리통계학 전공자 전원 대상

PDF로 다운로드(11.4MB): Sekei G. / 확률 이론 및 수학 통계의 역설

vixri.com

그리고 그 자신은 최소한 자신의 말로 무언가를 쓸 수 있습니까? 아니면 링크용이 아니라 스크린샷용입니까?

이제 나는 책을 읽으러 달려갔다. 이러한 역설의 대부분은 문제의 잘못된 공식화에서 작성자의 언어에서 발생합니다. 공을 날려 버리고 두뇌를 움직여야하며 역설이 없습니다.

1234567
새 코멘트