金融時系列の予測

－はじめに

本稿ではニューラルネットワークのもっとも一般的な実用的アプリケーションの一つ、市場の時系列予測、を取り上げます。この分野において、予測はもっとも密接に利益性と関連し、ビジネス活動の一つであるとみなすことができます。

金融時系列の予測はあらゆる投資活動に必要とされる要素です。将来利益を得るために今資金を投入する、という投資そのもののコンセプトは、将来予測のコンセプトに基づいています。そのため、金融時系列の予測は、組織化された為替やその他有価証券の取引システムといった投資業界全体に根差すものです。

この予測産業のスケールを物語る数値をいくつか提供します（Sharp, 1997）。米国株式市場の日次売上高は100億ドル（米）を超えます。11兆ドル（米）という金額（全額米ドル18兆ドルのうち）で有価証券が登録されている米国の預託信託会社は日々約2,500億ドル（米）を記録しています。世界的な FOREX の取引はもっと活発です。その日次収益は1兆ドル（米）を超えます。それは全世界の総資本のおよそ 50 分の 1 です。

全トランザクションの99% は投機であることが知られています。すなわちそれらは実際の商品循環に貢献するためではなく、『安く買い高く売る』というスキームから利益を得るために行われているのです。それらは取引を行う者によるレート変化予測を基にしています。同時に、そしてひじょうに重要なことですが、取引すべての参加者による予測は一様ではありません。投機取引のボリュームは市場参加者の予測相違の尺度、すなわち、現実には金融時系列の予測不能の尺度、を特徴づけます。

このもっとも重要な市場時系列の特性は、1900年にLouis Bachelier によって出された論文にある効率的な市場仮説に根差すものです。この説によると、投資家はダウ・ジョーンズや S&P500（ニューヨーク取引所）といった指数を利用して予測される平均市場の利益性を期待するのみです。ただし、投機的利益はすべて無作為に発生し、それはギャンブルのようなものです。市場曲線の予測不可能性は、交通量の多い通りの地面に落ちているお金がほとんどみつからないのと同じ理由で判断されます。見返りなくそれを拾う人が多すぎるのです。

有効な市場理論は市場参加者そのものからは当然ながら支持されていません（かれらはまさにこの『落ちている』お金を探しているからです）。その大半は市場時系列は、あてずっぽうに見えても、隠れた規則性がある、すなわちそれらは少なくとも部分的に予測可能である、と確認しています。1930年代にそうした隠れた経験的規則性を探し出そうとしたのは、テクニカル分析の創始者である Ralph Elliott でした。

1980年台、この観点により、少し前に出た力学カオス理論で驚くべき裏付けが発見されました。この理論はカオス状態と偶発性（無作為）の対立に基づいています。一連のカオスはただランダムに見えますが、決定された動的プロセスとして、それは短期的予測の余地がかなりあります。実現可能な予測領域は 予測期間により時間内に制限されているが、それは予測により実利を得るには十分なものかもしれない（Chorafas, 1994）。そうすると、ノイズのある一連のカオスから規則性を抽出するより良い数学的手法を持つ者はより良い利益率を期待するでしょう。自分達に劣る手法しか持たない者を犠牲にして。

本稿では、金融時系列を部分的に予測することを裏付ける特定の事柄を提供し、この予測性を数字で評価もします。

テクニカル分析とニューラルネットワーク

ここ数十年間に、テクニカル分析－多様な市場動向インディケータを基にした実験的ルール、はますます盛んになっています。テクニカル分析は、別の商品とは関連性なく、既定の商品の個別の変動に注意を集中する（Pring, 1991）のです。

この方法は、心理学的に、所定の時間に取引をしている対象の銘柄だけに対するブローカーの集中に基づきます。著名なテクニカル分析家（最初は心理療法士として訓練を受けた）である Alexander Elder 氏によると、市場コミュニティの動きは、群衆心理の特別な法則によって特徴づけられる群衆行動とひじょうに似ている、というのです。群衆効果は思考を単純化し、個人の特性レベルを下げ、個人のものより原始的な集団的な行動を生み出します。特に社会的本能がリーダー、アルファオス／メスの役割を強調するのです。Elder 氏によると価格曲線は、市場の集合意識そのものに集中しているリーダーそのものなのです。市場価格動向のこの心理学的解釈は、例の力学カオス理論を証明するものです。市場の部分的予測性は、比較的小さな内部自由度を持つ単一のカオス力学システムを形成するプレーヤーの比較的原始的な集団行動によって決定されるのです。

教義によれば、集団の『絆から離れる』こと、そしてそれを超え、市場曲線を予測できる集団より賢くなる必要があるのです。このためには、時系列の以前の動向について評価される ギャンブルシステムを開発し、感情や既存市場に渦巻く噂に影響されずに、このシステムに厳格に従うことです。別の言い方をすると、予測はアルゴリズムに基づくべきであるのです。すなわちそういったことはコンピュータに引き渡すことができる、もとい引き渡すべきである（LeBeau, 1992）のです。人間はこのアルゴリズムの作成だけ行うので、その目的のために人は、開発を促し、のちにテクニカル分析に基づきプログラムされた戦略を支援する多様なソフトウェア製品を手にしているのです。

この理論によると、戦略開発段階でなぜコンピュータを利用しないのか、です。コンピュータの存在は、既知の市場指標の計算や既定の戦略を検証するヘルパーではなく、インディケータの発見に対して最適なインディケータや最適な戦略を見つけ出すためのものなのです。ニューラルネットワーク技術のアプリケーションにサポートされるこの方法は、数多くの明白なメリットにより、90年台初頭より（Beltratti, 1995、Baestaens, 1997）どんどんフォロワーを勝ち取ってきています。

まず、ニューラルネットワーク分析はテクニカル分析とは異なり、入力データの性質に制限がありません。それは既定の時系列のインディケータと、その他の市場証券の変動に関する情報のどちらでもありえます。理由がないわけではなく、これらはニューラルネットワークを積極的に利用する機関投資家（たとえば大規模な年金基金など）です。そういった投資家は、異なるマーケット間の相関関係がもっとも重要である大規模なポートフォリオと連携します。

次に、一般的な推奨によるテクニカル分析とは異なり、ニューラルネットワークは所定の銘柄に対して、最適なインディケータを見つけ、それを基に　また再び所定の 時系列に対して戦略を最適に予測することができます。そのうえ、これら戦略には適応性があり、市場とともに変化します。それは若くダイナミックに発展する市場、特にロシア市場にとってはもっとも重要なことです。

ニューラルネットワークのモデル化そのものは、演繹的な考慮事項はなんら関与しないデータのみを基にしています。そこにニューラルネットワークの強みがあり、同時にそれがアキレスのかかとでもあります。有効なデータは学習に不十分で、潜在的入力の次元性は高すぎることがわかります。本稿でのちに、テクニカル分析で蓄積されてきた経験がどのように金融予測の分野に典型的なこの問題を乗り越えるのに役立てるかお見せします。

時系列予測手法

第1ステップとして、ニューラルネットワークを用いて時系列予測の一般的なスキームを説明します（図1）。

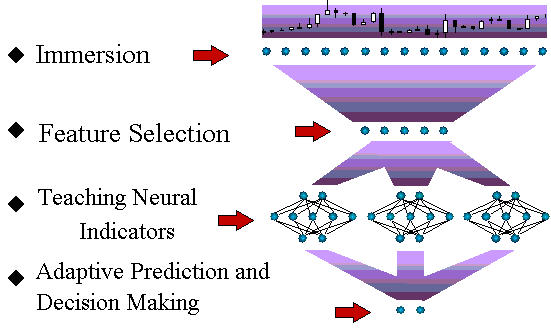
図1　時系列予測の技術サイクルスキーム

本稿でのちにこのプロセスフローの全段階を簡潔にお話しします。ニューラルネットワーク モデル化の一般原則は本タスクに完全に適用可能であっても、金融時系列の予測には特殊な性質があります。本稿ではこの特殊な性質をできる限り説明していきます。

イマーション テクニック　－タケンスの定理

イマーション段階から始めます。ここでわかるように、予測はデータの 外挿のように思えますが、ニューラルネットワークは確かに 内挿の問題を解決し、それはソリューションの妥当性を大幅に高めるものです。時系列の予測は、時系列を多次元空間に浸す 手続きを用いて、ニューラル分析－所定の例に対する他変数関数の概算－のルーチン問題に変化します（Weigend, 1994）。たとえば、時系列のある次元ラグ 空間は時間の連続した瞬間に時系列値で構成されます。

.

以下のタケンス定理は動的システムに対して証明されます。時系列が動的システムによって生成される、すなわち の値がそのようなシステムの状態の任意の関数であれば、そこには時系列の次の値の 明白な予測値を提供する浸漬深度（おおよそこの動的システムの自由度の実効的な数に等しい）が存在する（Sauer, 1991）のです。よって、かなり大きなものを選択すると、時系列の将来値と先行値の間に名はウナ依存を保証することができるのです。すなわち、時系列予測は他変数関数内挿の問題に変わるのです。そして、ニューラルネットワークをこの時系列の履歴によって定義される例のセットに基づく未知の関数を復元するために利用することができるのです。

逆に、ランダムな時系列については、過去の知識は未来を予測するためになんら有用なヒントは提供してくれません。よって、効率的市場理論に基づき、予測ずみ時系列値の分散はラグ空間に入れても変化はありません。

浸漬中のカオス力学と確率（ランダム）動力学の間に検出される違いは図2に示しています。

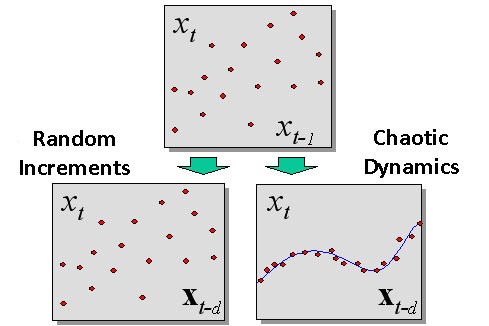
図2 　浸漬中に検出されるランダム過程とカオス力学の間の違い

時系列予測性の経験的証明

浸漬手法により実際の証券の予測性を量的に測定することができます。すなわち、効率的市場仮説を証明または反駁することができるのです。後者によると、すべてのラグ空間座標における点の発散は、同様であります（点が同様に分布されている個別の無作為な値であれば）。逆に、一定の予測性をもたらすカオス力学は、観測が一定の超表面の周辺に集まっていることに導きます。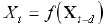すなわち、実験サンプルはラグ空間全体の次元よりも小さな次元セットを形成するのです。

次元を測定するには、以下の直観的特性を利用します。あるセットの次元が D である場合、 の辺を持つより小さな立方体の表面に分割されると仮定すると、その立方体の数は のように増えます。これは、前回の考察からわかっているボックスカウンティング法によりセットの次元を検出する基礎になります。一式の点の次元は、セットの点すべてを含むボックスの数が増える割合により検出されます。アルゴリズムの速度を上げるために、2の倍数として 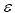の次元を取ります。すなわち、解像度スケールはビットで測定するのです。

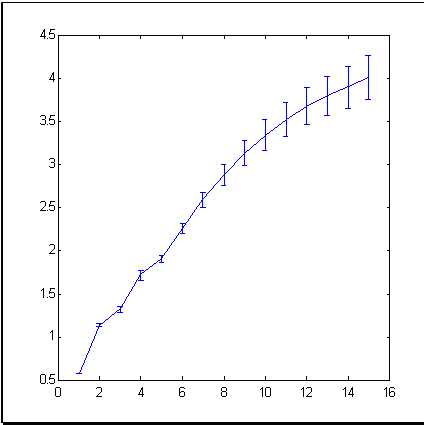
典型的な市場時系列の例として、ニューヨーク市場の平均価格変動を反映する良く知られたファイナンシャルツールである S&P500 指数を採用します。図3 は679か月の期間における指数変動を表示しています。ボックスカウンティング法で計算されたこの時系列の増分の次元（情報次元を意味します）は、図4に示しています。

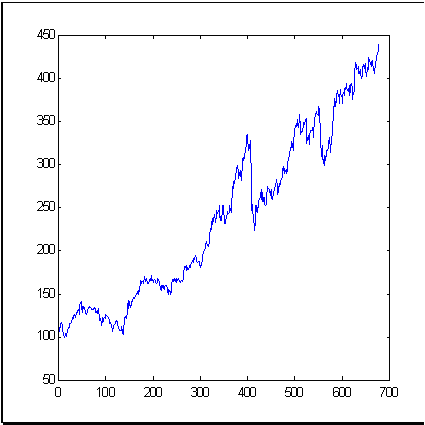
図3 　S&P500 の679の値の時系列（本稿での例として）		図4 　 S&P500 時系列の増分の情報次元

図4から次のとおり、実験的ポイントは15次元の浸漬空間において約4の次元セットを形成しています。これは、増分の時系列を独立した ランダム値であるとする効率的市場理論に基づきて取得される15からはかなり小さなものです。

よって、完全に決定されたカオス力学がここにあるとは主張できないものの、経験的データは金融時系列において一定の予測可能な構成要素の存在があるという説得力ある証拠を提供しています。市場予測に対してニューラルネットワーク分析を適用する試みには強い根拠があります。

ただし、理論的予測可能性は予測の実用的に優位なレベルを保証するものではないことに注意が必要です。特定の時系列の予測可能性の定量的評価は クロスエントロピーを測定することで取得可能です。それにはボックスカウンティング法を用いることも可能です。たとえば、S&P500 の増分予測を浸漬深度に関連して測定するのです。クロスエントロピー

,

以下がクロスエントロピーのチャートです（図5）。時系列の次の値に関する追加情報を測定します。それはこの時系列の前の値を知ることでサポートされています。

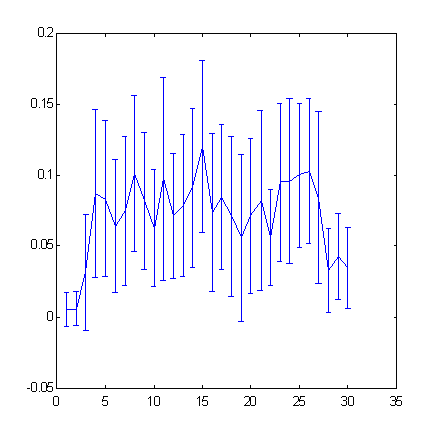
図5 　浸漬深度（『ウィンドウ』幅）に関連しての S&P500 の時系列に対する増分符号の予測

浸漬深度を25より大きく増加すると、予測性を減少させることになります。

実質的に予測可能性のそのようなレベルに達する利益をさらに評価します。

属性の入力空間形成

図5では、時系列浸漬ウィンドウの幅を広げることは、最終的には予測可能性を下げる結果になることがわかります。入力次元の増加はもはや情報値で補われることはないのです。この場合、ラグ空間次元が例で与えられる数よりも大きすぎると、小さな次元で属性のスペース を形成する特殊な方法を使用する必要があります。属性選択および／または有効な例の数量を増加する金融時系列特殊方法は以下で説明します。

エラー機能の選択

ニューラルネットワーク学習を作成するのにインプット／アウトプットのティーチング セットを形成するのでは十分ではありません。ネットワーク推測エラーも決定する必要があります。デフォルトでほとんどのニューラルネットワーク アプリケーションに使用されている二乗平均平方根誤差には、市場時系列に対する『金融的センス』があまりありません。これが記事の特別な項目で特に金融時系列の固有エラーを考察し、可能な利益率に関連付ける方法をお見せする理由です。

たとえば、市場ポジションを選択するためのレート変化の兆候を確実に検出することは、平均二乗偏差を減らすことよりもずっと重要です。これら指数が互いに関連していても、そのうちの一つに対して最適化されたネットワークはもう片方について悪い予測を出します。本稿でのちに証明する適切なエラー関数を選択することは、一定の理想的な戦略に基づき、たとえば利益を最大化したい（または潜在的損失を最小化）という願望によって決められます。

ニューラルネットワーク学習

時系列予測の主要な特徴はデータの前処理フィールドにあります。個別のニューラルネットワークに対するティーチング手順は標準的なものです。通常どおり、有効なパラメータは3つのサンプルに分けられます。それは学習、有効化、検証です。1番目は、ネットワーク学習に使用されます。2番目は最適なネットワーク構造の選択および／またはネットワークのティーチングを停止するタイミングの選択に使用されます最後、ティーチングにはまったく使用されなかった3番目は『トレーニングされた』ニューラルネットワークを制御する質を予測するのに役立ちます。

ただ、ひじょうにノイズの多い金融時系列に対して、 グループニューラルネットワークの使用は大幅に予測の信頼性が高まる結果となります。本稿のしめくくりはこの手法についての話題となります。

研究の一部では、フィードバックニューラルネットワークにより、予測の質がより良いものとなっている証拠も見つけることがあります。そのようなネットワークはインプットで明示的に有効なデータよりもずっと過去にさかのぼったデータを保存するローカルメモリを持ちます。ただし、そのような構造を考えることは、本題からの逸脱となり、以下で説明する特殊な時系列浸漬手法によりネットワークの『水平線』を効率的に広げる代替手法があるため、余計にそうなってしまいます。

属性スペースの形成

インプットの効率的なコーディングは予測の質を上げるためのポイントです。それはほとんど予想のつかない金融時系列にとっては特に重要です。データの前処理について標準的な推奨事項はすべてこちらで適用できます。ただ、データ前処理の金融時系列特有の方法があり、本項ではそれを詳しく考察していこうと思います。

時系列浸漬法

まず、クオート値それ自体を使用してはならないことを心に留める必要があります。それは として指定するもので、ニューラルネットワークのインプットまたはアウトプットです。予測には実に重大なクオート変化があります。一般的にこういった変化はクオート自体よりももっと小さな範囲にあるため、レート値の間には強い相関関係が存在します。－レートのもっとも予測できる次の値は、その前の値に等しい：、となるのです。同時に、繰り返し強調されるように、学習クオリティーを高めるために、インプットの統計的独立性に努める必要があります。

これは、インプットとして統計的にもっとも独立している値を選択するのが理論的である理由です。たとえばクオート変化、 または相対増分対数です。後者の選択は、インフレの影響が顕著に目立つ長期的な時系列には都合のよいものです。この場合、系列のシンプルな同意部分は異なる範囲にあります。事実、それらは異なる単位で測定されるためです。逆に連続クオート間の比率は測定単位に依存せず、インフレのため測定単位が変化しても、それらは同一尺度を持ちます。結果、時系列の大きな定常性によりティーチングに大きな履歴を使用でき、より良い学習が行えるのです。

ラグ空間に浸漬するデメリットは、ネットワークの限られた『水平線』です。逆に、テクニカル分析は過去のウィンドウ は固定せず、ときとして時系列のひじょうに遠い値を使用することもあります。たとえば、比較的遠い過去から採られた時系列の最大値、最小値はトレーダーの心理にかなり強い影響を与え、そのためこういった値は予測にはまだ有意であると主張されます。ラグ空間に浸漬するために不十分なウィンドウ幅は、自然に予測の効率を下げるような情報を提供しません。一方、距離を縮める値、時系列の極値、に対してウィンドウを広げることでネットワーク次元が増加することとなります。これはこんどは、ニューラルネットワークの予想の精度を下げることにつながります。それはここでのネットワークの成長のためです。

この頭打ち状況ともいえるものから抜け出すには、時系列の過去の変化をコーディングする代替方法を用いることです。時系列履歴を遠くまで遡るほど、その変化が予測結果に及ぼす影響が低くなることは直観的に明らかです。これは、厳密に言えば、将来を形成するトレーダーによる過去の主観的認知により決定されるものです。そのため、そのような時系列の表現を見つける必要があります。それは、選択的精度を持つものです。過去にさかのぼるほど、詳細ではなくなるのです。同時に、曲線の一般的表示は完全なままでないといけません。いわゆるウェーブレット分解がここではひじょうに有望です。その情報値はラグ浸漬と等しくなっていますが、過去が選択精度を伴って記述されるという方法でデータを圧縮する方が簡単になります。

インプットの次元低減：属性

このデータ圧縮は、過度に大きなインプット変数の数から予測するのに最も重大な属性を抽出する一例です。属性を系統的に抽出する方法はすでに上で説明しました。それらも時系列予測に連続的に適応することが可能です（そしてする必要があります）。

インプットの表現がおそらくデータ抽出を容易にするということは重要です。ウェーブレット表現は優れたコーディングの一例（属性抽出の観点から）である（Kaiser, 1995）のです。たとえば、次のグラフ（図 6）は、10 個の特別に選択されたウェーブレット相関により再構築された時系列の 50 の値のセクションを表示しています。5倍少ないデータを必要としたにもかかわらず、時系列の一番近い過去は正確に再構築されており、一方で遠い過去は正確に高値と安値を反映している概要で復元されていることにご注意ください。そのため、許容可能な精度で10次元インプットベクトルを持つ50次元ウィンドウを記述することが可能なのです。

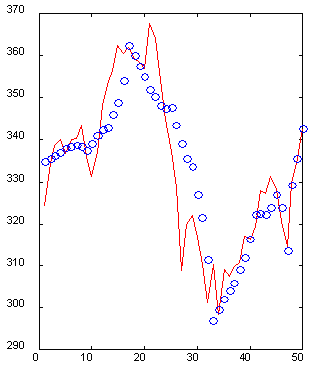
図6 　50次元ウィンドウ（実線）と、10のウェーブレット相関（o）によるその復元例

もう一つ可能性ある方法は、属性空間の潜在的候補として、適切なソフトウェア パッケージ（MetaStock または Windows On Wall Street)）で自動的に計算されるさまざまなテクニカルインディケータを使用することです。所定の時系列に応用するなら、それぞれは便利であることがわかりますが、そのような経験的属性（Colby, 1988）の大きな数字は、使用を困難にします。上記で述べられている方法により、ニューラルネットワークのインプットとして使用するテクニカルインディケータのもっとも有意な組み合わせを選択することができます。

ヒント法

金融予測における最も弱い点の一つは、ニューラルネットワーク学習に対する例の欠如です。一般的に言うと、金融使用（特にロシア市場）は定常ではありません。まだ履歴がまったく蓄積されていない新しい指数があるようで、時間とともに古い市場での取引の性質は変化するのです。こういった条件で、ニューラルネットワーク学習に有効な時系列の長さはかなり限られています。

ただ、時系列力学の不変量について先験的な配慮をいくらかすることで例の数を増やすことができます。これは、金融予測の質を大幅に高める別の物理数学用語です。問題は、既存のものに様々な変換を加えることでそこから取得される人工的な例（ヒント）を作成することです。

例によって主要な考えを説明します。以下の仮定は心理的に合理的なものです。トレーダーは、軸上の特定の値ではなく、価格曲線に注意を向けることが多いものです。よって、クオート軸に沿って時系列をわずかばかり伸ばすと、そのニューラルネットワーク学習に対するその変換（最初のものと共に）から得られる時系列を利用することができるようになるのです。そのため、トレーダーがどのように時系列を知覚するかという心理的特性からもたらされる先験的情報を用いることで、例の数を倍増させました。また、例の数を増やすとともに、その中でソリューションを検索する関数クラスを制限しました。それは予想のクオリティーを高めることでもあります（もちろん利用される不変量が事実に対して真である場合）。

以下（図 7、8 をご覧ください）に表示された。ボックスカウンティング法により S&P500 の予測可能性を計算した結果はヒントの役目を示しています。属性空間はこの場合、直交化技術によって作成されました。100 次元のラグ空間でインプット変数として 30の主要な構成要素を使用しました。そして、この主要な構成要素から7個の属性を選択しました。もっとも有意な直交直線の組み合わせです。以下の図からわかるように、この場合、ヒントのアプリケーションだけが顕著な予測を提供できることが判明しました。

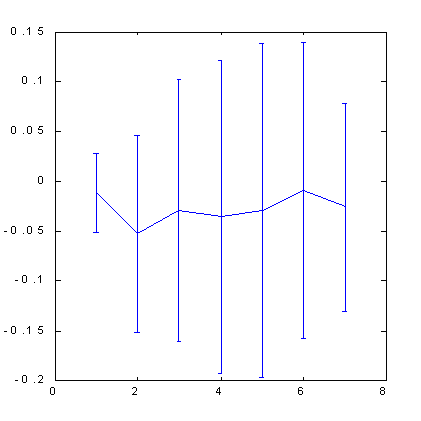
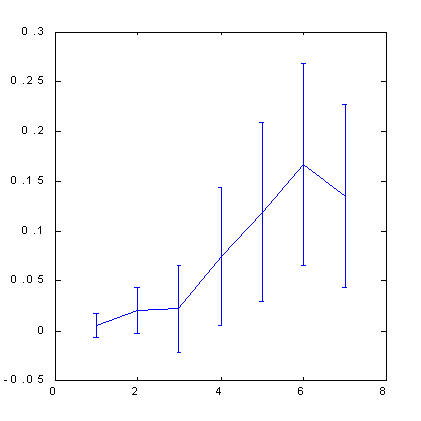
図7 　S&P500 に対するクオート変化の兆候予測可能性

図8 　数多くの例のあとの S&P500 に対するクオート変化の兆候予測可能性後は価格軸を伸ばすことで 4 倍になりました。

直交空間の使用により、標準的な浸漬手法に比べ一定の予測可能性向上を導くことに留意ください。0.12 ビット（図 5）から0.17 ビット（図 8）です。少し後、利益に関する予測可能性の影響の話を始めるとき、このことで利益率がふたたび半減することを証明します。

ニューラルネットワークがどの方向でソリューションを検索するのかについてのヒントをうまく利用できた重要なもうひとつの例は、外国為替取引における隠れた対称性を利用することです。この対称性という意味は、外国為替のクオートは2つの『視点』から考察されるというものです。たとえば、一連 のDM/$ や、 $/DMです。そのうちの一方を増やすことはもう片方を減らすことになります。この特性は例の数を倍増するのに利用できます。対称類似体 を のような例それぞれに追加するのです。ニューラルネットワーク予測の実験は、基本的な外国為替市場に対して、特に対象性を考慮することで利益率をおよそ2倍に増やすことを示しました。実際の取引コストに配慮して、年間 5% から 10% です（Abu-Mostafa, 1995）。

予測クオリティーの測定

金融時系列の予測は多次元関数近似化問題に変わるとはいうものの、インプットを作り、ニューラルネットワークへのアウトプットを選択するというそれ自体の特殊な性質を両方持ちます。インプットについては上ですでに考察しました。ですから、ここではアウトプット変数を選択するという特殊な性質を詳しく調べます。ですがまず、主要な質問に答える必要があります。金融予測のクオリティーはどのように測定できるのでしょうか？これは、ニューラルネットワーク学習のベストな戦略を見つけるのに役立つのです。

予測可能性と利益率の関係

金融時系列予測の特殊な性質は最大の利益を得る作用で、関数の近似化で従来よくあるように、平均二乗偏差を最小に抑えることではありません。

日々の取引のもっとも単純なケースでは、利益はクオート変化の兆候 を正しく予測することで決まるものです。これが、ニューラルネットワークが値そのものよりも兆候の予測を正確に行うことを狙いとするゆえんです。日々の市場参入をもっともシンプルに行う上で、利益率がどのように精度を検出する兆候に関連しているか見つけます（図9）。

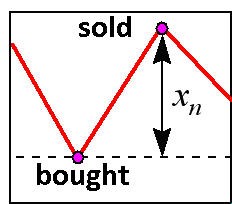
図9 　日次市場エンター

の時点で、トレーダーの最大資本が、相対的クオート変化が と指定します。そしてネットワークのアウトプットとして、この変化の兆候に対する信頼性あるレベル： を取ります。 の非線形形式のアウトプットを持つこのネットワークは、変化の兆しをどのように予測するか学習し、その確率に比例する範囲で兆候を予測します。そして 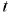段階のキャピタルゲインは以下のように記録されます。

ここで は『動作中』の資本分配率です。それは全取引期間
に対する利益です。
最適なレートサイズ 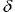を選択することでそれを最大化します。トレーダーに正確にサインの を予想させ、それに対応して、 の確率で誤った予想をします。そして利益率の対数、

,

と利益そのものは の値および平均においてもっとも高くなります。

.

ここで、の係数を取り入れました。たとえば、ガウス分布に対しては です。兆候の予想可能性レベルは、ボックスカウンティング法により先験的に見積もることのできるクロスエントロピーに直接関連しています。バイナリアウトプットに対しては以下です（図10 参照）。

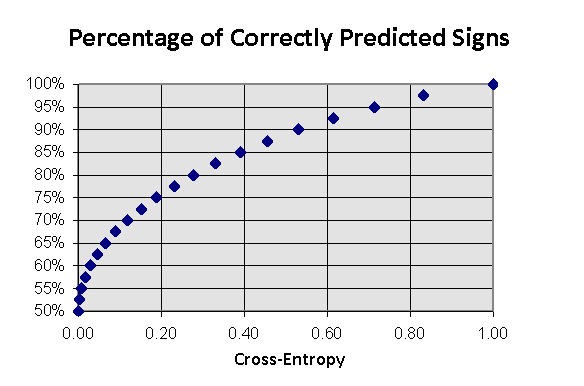
図10 　既知の入力に対する出力記号のクロスエントロピー関数としての時系列変化の正確な予測方向の端数

最終的に、以下のように、ビットで表現されるI の所定の記号予想可能性に対する利益率の推定を取得します。

それは、Iの予想可能性を持つ時系列に対して、原則的に 市場エンターにおいて資本を倍にすることが可能であることを意味します。よって、たとえば、前に計算された I=0.17 （図8参照）に等しい S&P500 の時系列予想可能性は、 市場エントリーについて平均で資本を倍にするとされます。そのため、小さなクオート変化兆候の予測可能性もひじょうに驚くべき利益率を出す可能性があるのです。

ここで、最適な利益率には、市場エントリーのたびにトレーダーが厳密に定義された資本のシェアを危険にさらす場合、かなり注意して取引を行うことが必要であることを強調しておきます。

,

ここで はこの市場の変動性 に対する一般的な利益／損失サイズです。比率の大小の値はどちらも利益を減らします。リクスの高い取引はどんな予想可能性においても資金を失う結果につながりうるのです。この事実は図11で説明がされています。

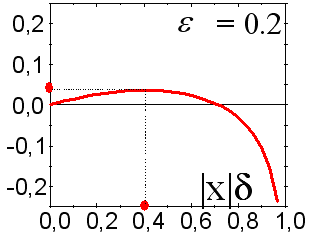
図11 　『kitty で』選択された資本シェアから得る平均利益率の依存

これは上の推定値が利益率の上限だけに洞察をする理由です。揺らぎ効果をもっと注意深く考察することは本稿の範囲を超えてしまいます。ただ、契約サイズを最適に選択するには、各段階で正確に予測する必要があることは定性的に明確です。

エラー機能の選択

利益を最大化するために金融時系列を予測することにしたら、ニューラルネットワークをこの最終結果に合わせて調整することは理にかなっています。たとえば、上で述べたスキームに従ってトレードする場合、すべての学習サンプルにより平均化された以下の学習エラー関数をニューラルネットワーク学習に対して選択するのです。

.

ここで、取引中の資本シェアは学習中に調整する追加のネットワークアウトプットとして取り入れます。この方法には、活性化関数 を持つ第1のニューロンである は比率を上下する確率を出します。そして第2のネットワークアウトプットであるは所定の段階で投資する推奨される資本シェアを生み出します。

ただし、前の分析によると、このシェアは予測の信頼水準に比例するため、2つのネットワークアウトプットを を設定することでただ一つと置き換え、エラーを最小化する唯一のグローバルパラメータである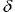の最適化に限定します。

これは、ネットワークによって予想されるリスクレベルに従い比率を調節する機会を産み出します。変動金利を扱うことで固定金利よりも利益が出るのです。確かに、平均的な予測可能性で決めて金利を固定すると、資本増加率はに比例します。一方で、各ステップで最適な金利を選択する場合、それは に比例します。

グループネットワークの使用

一般的に言うと、同一サンプルについてトレーニングされた異なるネットワークによる予想値は、異なります。これはシナプス重量の初期値を選択するランダムな性質のためです。この欠点（不確実な要素）は、異なるニューラルネットワークで構成されるグループ ニューラル エキスパートを作成することでメリットにすることができるのです。エキスパート予想値のこの分散は、これら予想値の信頼水準の考えを提供します。それは正しいトレーディング戦略を選択するのに使用するものです。

グループ値平均が同一グループの平均的エキスパートよりも優れた予測をすることを証明するのは簡単です。のインプット値に対して i番目のエキスパートのエラーをに等しくします。グループの平均エラーは、コーシーの不等式から、つねに個別のエキスパートの平均二乗エラーよりは小さくなります。

.

エラーの削減はかなり基礎的であることに注意を払います。個別のエキスパートのエラーが互いに相関しなければ、すなわちであれば、Lエキスパートで構成されるグループの平均二乗エラーが1件のエキスパートの平均の個別エラーより倍小さいのです。

これは予測をグループ全体の平均値を基にするほうが良いことの理由です。この点は図12で説明されています。

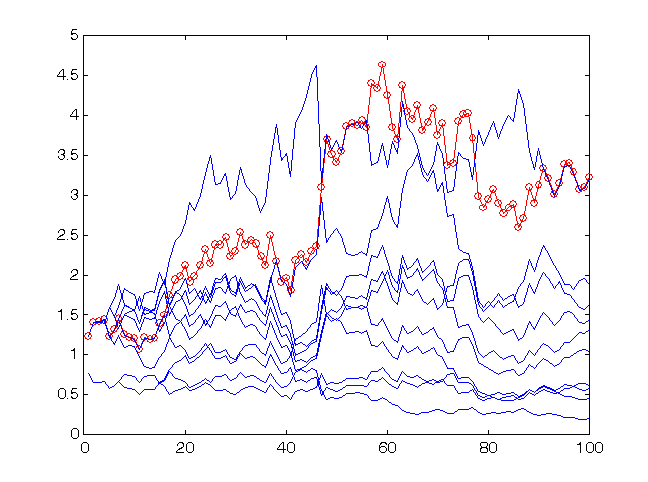
図12 　10個のネットワークによるグループで予測するとき、時系列 sp500 の最終100の値に対する利益率

グループ（サイクル）の利益は平均的エキスポートより高くなります。グループに対して正しく予想された記号のスコアは 59:41 です。

図12からわかるように、この場合、グループの利益は各エキスパートよりも高くなっています。よって、グループ手法は基本的に予測クオリティーを上げるのです。利益率の絶対値に注意してください。グループ資本は、市場エントリー100で 3.25 倍増えました（この比率は「もちろん取引コストが考慮されれば低くなります）。

予想値は、インデックスインクリメント時系列の 30 の連続する指数移動平均（EMA 1 … EMA 30）におけるネットワーク学習時に取得されました。次のステップにおけるインクリメントサインは予想されました。

この実験では、金利は所定の予測精度（正確な予想サイン59対不正確な予想サイン41）に対する最適化レベルに近いレベルに固定されました。すなわちです。図13で、同じ予想値でのよりリスクの高い結果、すなわちをもつ、を確認できます。

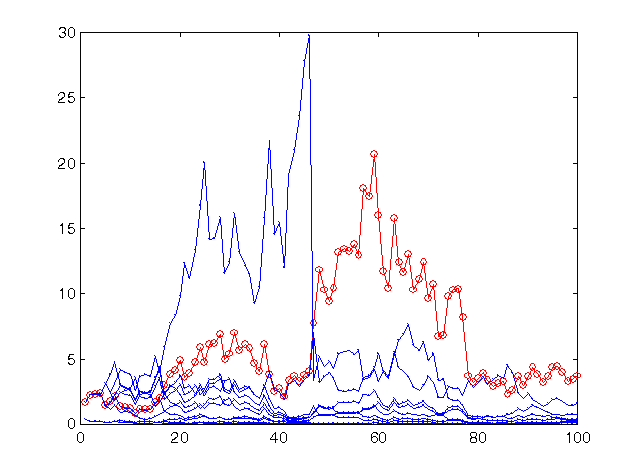
図13　同一の10個のネットワークでリスクのより高い戦略を用いて予測する場合の時系列の最終100の値に対する利益率

グループの利益は同じレベルに留まっています（やや高く）。このリスク値が前回のものと最適値に近いためです。ただ、全体としてグループの予想値より精度が劣る大半のネットワークにとっては、その金利はリスクが高すぎることがわかります。それは実質的にすべてを損なうものです。

上記の例は、予測クオリティーを正確に推定できることがどれほど重要か、またこの推定値が同一予想値の集積性を増やすためにどのように利用できるのかを示しています。

もっと大きな極値に行って平均 ではなくエキスパートネットワークの加重 意見を使用することも可能です。重量は、学習サンプルにおけるグループの予想能力を最大化し、適応的に選択します。結果として、トレーニングの悪いグループネットワークは小さな分布となり、予想値を損なうことはありません。

この方法の可能性は、25個のエキスパートで構成されるグループネットワークの2タイプによる予想値を以下で比較することで説明されます（図14および図15）。予想は同一スキームに従って行われました。インプットとして、最初の10個のフィボナッチ番号に等しい期間で時系列の指数移動平均が使用されました。100の実験から取得した結果によると、加重予想は正しい予想サインが正しくない予想サインを平均的に超え、ほぼ15に等しく、一方で平均予想に対するこのファクターは約12です。一定期間内の減少率と比較して、価格上昇の総量は正確に 12 に等しいことに留意が必要です。よって、増加の主な傾向を "+" 記号の些細な一定の予測値とみなすことは、正しく予想されている比率への同一結果を25個のエキスパートの加重意見として出すこととなるのです。

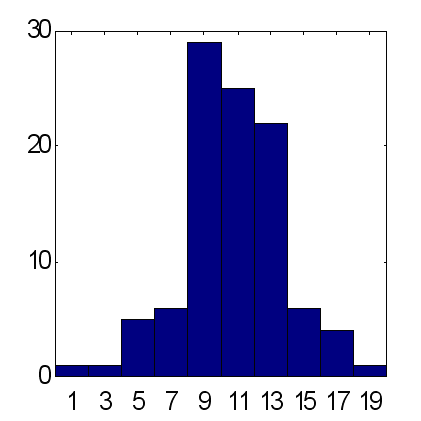
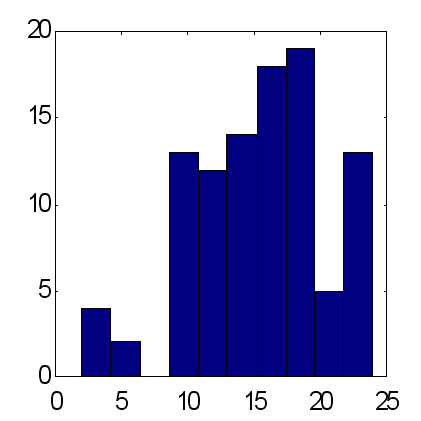
図14　25のエキスパートの平均予測における正確に予想された合計のヒストグラム3.2の標準偏差における100グループに対する平均 = 11.7 です。

図15 　25のエキスパートの加重予測における正確に予想された合計のヒストグラム4.9 の標準偏差における100グループに対する平均 = 15.2 です。

ニューラルネットワーク予測値の可能性ある利益率

これまで、数値実験の結果を正しく予想した兆候としてパーセントで表現してきました。ニューラルネットワークを使用してトレードを行う際、現実的に到達可能な利益率を見出します。変動を顧慮せず上記で取得された利益率の上限は、実際にはほとんど到達できるものではありません。達成される予想レベルを相殺する前に取引コストを考慮していなければ余計にそうなります。

実質上、コミッションを考慮することで減衰定数のようになります。

そのうえ、予想レベル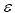とは異なり、コミッション は二次的ではなく線的に入ります。そのため、上記の例では、予測可能性の典型的な値 はコミッションを超えることはできません。

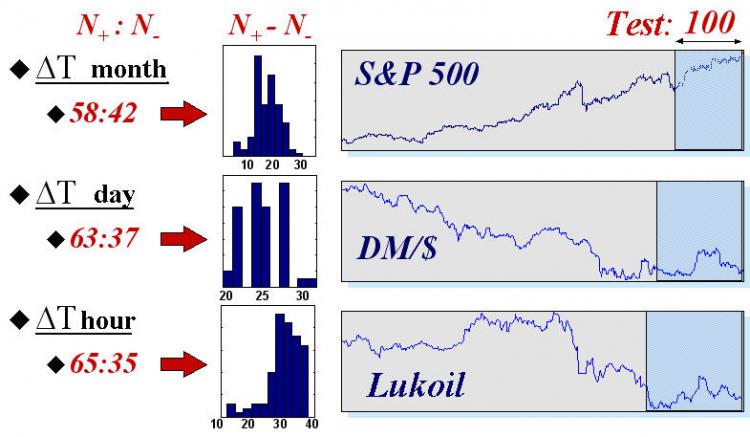
この分野でのニューラルネットワークのほんとうの可能性の考えを提示するために、異なる典型的な時間で3つの指数についてニューラルネットワークを用いた自動トレーディングの結果を出します。3つとは、読み出しに 毎月の間隔を持つ指数S$P500 の値、DM/$ の日次クオート、ロシア市場における Lukoil 株に対する毎時の先物読み出しです。予測の統計は、50の異なるニューラルネットワークシステムから収集されました（各50のニューラルネットワーク グループを持ちます）。時系列自体と各時系列の最終100個の値の検証セットにおける兆候の予測結果は図16に表示しています。

図16 　3つの実金融指数の100個の値の検証サンプルにおいて正確に（ ）また不正確に（ ）予想した数値の平均値およびヒストグラム

この結果は直観的に明確な規則性を裏付けるものです。それは、時系列に予想可能性があるほど、読み出し間隔は小さくなる、というものです。実質上、時系列の連続値の間で経過する時間が長ければ、その変化に向かう外部情報が市場参加者にとって有効になり、そしてそのため、時系列自体が持つ将来の情報は少なくなります。

そして上で取得された予想値は検証セットのトレードに使用されました。同時に、各ステップの契約サイズは予想の信頼度に比例して選ばれ、グローバルパラメータ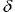の値は学習サンプル上で最適化されました。そのうえ、それがうまくいったことで、グループの各ネットワークは独自の浮動評価を得ました。各ステップにおける予測では、ネットワークの実際に『ベスト』な部分だけ使用しました。そのような『ニューラル』トレーダーの結果は図17に示しています。

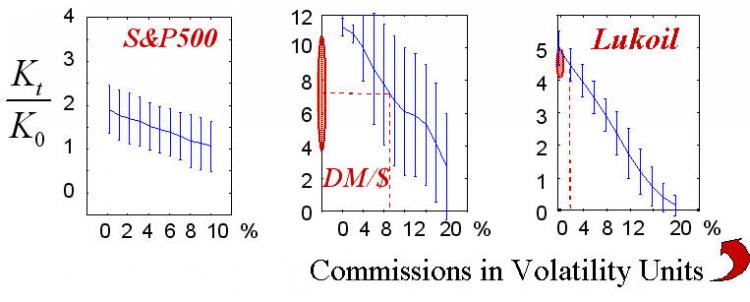
図17 　コミッション額に従った50件の実行の勝利統計

破線で引かれているコミッションの実値は現実に到達可能な利益率の領域を示しています。

最終勝利（ゲームの戦略自体のように）はもちろん、コミッションサイズにより決まります。上の図でしめされているのはこの依存性です。私が知る測定単位として選択された中のコミッションの現実的値は、図の中でマークしています。実トレードの『量子化された』性質はこの実験では考慮されていない、すなわちトレードサイズは一般的契約の整数に等しくなる、ということを考慮していなかった、点は改善する必要があります。この場合は一般的トレードが数多くの契約を持つ大規模資本をトレードすることに対応しています。また、保証取引が暗示されていました。すなわち、利益率は契約そのもののスケーリングよりはるかに小さい安全資本 に対する比率として計算されました。

上の結果はニューラルネットワークに基づくトレードは、少なくとも短期間ではひじょうに有望であることを示しています。そのうえ、金融予測の自己相似性を考慮すると（Peters, 1994）、時間単位の利益率はより高く、一般的トレード時間は少なくなります。よって、ニューラルネットワークを使用した自動トレードは一般的ブローカーをしのぐメリットが顕著であるリアルタイムもー9度でのトレーディングの際、もっとも効率的であることがわかります。そのメリットとは、耐疲労性、感情への非感受性、潜在的なより高い回答率、です。自動売買システムに接続されたよくトレーニングされたニューラルネットワークは、人間のブローカーが自身のターミナルでチャート上の価格変化を認識するよりもずっと簡単に意思決定を行うことができるのです。

おわりに

（少なくとも一部の）市場時系列は部分的に予想可能であることを示しました。その他のニューラル分析同様、時系列予測にはかなり複雑で注意深いデータ処理が必要です。ただし、時系列の処理には、利益を増やすために利用できる独自の特性があります。これはインプットの選択（データ表現の特殊な方法を用いて）とアウトプット選択、また特殊なエラー関数の利用に関連しています。最後になりましたが、個別のニューラルネットワークと比較することで、グループニューラルエキスパートを使用することがどれほど収益性を高めるか示しました。また、複数の実際の証券における実利益率も提供しました。

参照資料

• Sharpe, W.F., Alexander, G.J., Bailey, J.W. (1997). Investments. - 第6版、Prentice Hall, Inc., 1998.
• Abu-Mostafa, Y.S. (1995). "Financial market applications of learning from hints”. In Neural Networks in Capital Markets. Apostolos-Paul Refenes (Ed.), Wiley, 221-232.
• Beltratti, A., Margarita, S., and Terna, P. (1995). Neural Networks for Economic and Financial Modeling. ITCP.
• Chorafas, D.N. (1994). Chaos Theory in the Financial Markets. Probus Publishing.
• Colby, R.W., Meyers, T.A. (1988). The Encyclopedia of Technical Market Indicators. IRWIN Professional Publishing.
• Ehlers, J.F. (1992). MESA and Trading Market Cycles. Wiley.
• Kaiser, G. (1995). A Friendly Guide to Wavelets. Birk.
• LeBeau, C., and Lucas, D.W. (1992). Technical traders guide to computer analysis of futures market. Business One Irwin.
• Peters, E.E. (1994). Fractal Market Analysis. Wiley.
• Pring, M.G. (1991). Technical Analysis Explained. McGraw Hill.
• Plummer, T. (1989). Forecasting Financial Markets. Kogan Page.
• Sauer, T., Yorke, J.A., and Casdagli, M. (1991). "Embedology". Journal of Statistical Physics. 65, 579-616.
• Vemuri, V.R., and Rogers, R.D., eds. (1993). Artificial Neural Networks. Forecasting Time Series. IEEE Comp.Soc.Press.
• Weigend, A and Gershenfield, eds. (1994). Times series prediction: Forecasting the future and understanding the past. Addison-Wesley.
• Baestaens, D.-E., Van Den Bergh, W.-M., Wood, D. Neural Network Solutions for Trading in Financial Markets. Financial Times Management (July 1994).

記事は著者の同意を得て発表しました。

著者について：Sergey Shumskiy はロシア科学アカデミー物理学研究所 Cand.Sc. （物理学および数学）の上級研究員、機械学習と人工知能技師、ロシアニューラルネットワーク協会の幹部会メンバー、機械学習技術によって企業のエキスパートシステムを開発する、IQMen Corp の CEO です。Shumskiy 氏は 50 以上の科学出版の共著者です。
著者のコース：Neural Computing and Its Applications in Economics and Business