Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Non lo so, ho scritto qual è la formula e tutte le variabili sono definite. Lasciatemi anche chiarire - questa è la quantità di profitto presa ogni mese (non il profitto totale per m mesi).
Resta da ricavare la formula per la somma delle serie, hai scritto che lo fai facilmente - fallo. Poi prendere la derivata, equipararla a zero...
Nei miei termini, la vostra formula per il prelievo del mese corrente si presenta così:
Di conseguenza, scomporre la derivata bestiale di questa funzione è difficile come quella precedente.
Penso che si possa provare a pre-prologaritmizzare f e poi cercare il suo massimo... Forse sarà più facile così.
avtomat:
E poi, nella seconda fase, aprire la valvola che divide il flusso in due parti. Questo cambierà il flusso di ingresso.
Non vedi ancora la soluzione?
No, non so cosa stai pensando. Ditemi.
Ci sono alcuni che nemmeno il teorema di Pitagora, come interpretato da loro, può essere compreso.
OFFTOP:
A scuola hanno dato la prova più succinta del teorema di Pitagora.
Nota, l'idea di base più semplice (non standard) è p.2. Non viene utilizzata alcuna conoscenza delle proprietà dei triangoli simili, inoltre non è necessaria alcuna conoscenza della trigonometria per capire l'esistenza della funzione f. Cioè una tale prova può essere data nelle scuole elementari dopo aver spiegato bene (non come al solito) ai bambini cos'è l'area.
OFFTOP:
A scuola hanno dato la prova più succinta del teorema di Pitagora.
In quale grado?
La formula S = c^2 * f(alfa) non è ovvia per un bambino di 7 anni. È dare per scontato che lo sia.
Di conseguenza, rompere la derivata bestiale di questa funzione è altrettanto difficile di quella precedente.
L'intero processo è bloccato con il derivato?
Questa funzione è x0*k*(1-(1+q-k)^2)/(k-q)?
Se è così, è come se non ci fossero problemi, li ho risolti facilmente, ho solo bisogno di ricordare un po'. La variabile q?
in quale classe?
La formula S = c^2 * f(alfa) non è ovvia per un bambino di 7 anni. È dare per scontato che lo sia.
Quasi tutti i bambini che sono stati introdotti al concetto di area di una figura abbastanza bene da sentirlo, avranno poche difficoltà a capire la prova di cui sopra.
Se un bambino capisce veramente cos'è l'area, ne capisce la misura e capisce anche che l'area di qualsiasi figura può essere espressa attraverso le sue caratteristiche (in questo caso l'ipotenusa e l'angolo) che definiscono in modo unico la figura.
Non è necessaria alcuna conoscenza delle proprietà dei triangoli simili e della trigonometria.
Sono stato in visita di recente e ho visto due piramidi di pietra (simili alle piramidi egiziane). Li ho presi in mano e li ho messi alla loro base (sono di dimensioni leggermente diverse):
Ed è venuto fuori con un'altra prova del teorema di Pitagora (chiaro dalla costruzione).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
No, il problema è la derivata di k da: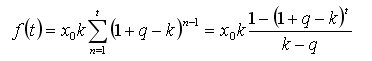
Deve essere equiparato a zero e risolto rispetto a k.
Non posso farlo in modo intelligente, quindi lo farò in modo semplice:
Diciamo che ci sono 10.000 sul deposito all'inizio del periodo. Ogni periodo aggiungiamo il 5% al deposito e lo reinvestiamo nel deposito. Ogni periodo ci è permesso di prelevare solo il 3%.
Se ritiri tutto il 3% dei tuoi soldi ogni periodo, tutti noi otteniamo più di 4k$ (e non ce ne frega un cazzo del deposito), altrimenti otteniamo solo 0.5k$ (ma con molto sul deposito).
Quasi tutti i bambini che sono stati introdotti al concetto di area di una figura abbastanza bene da sentirlo, avranno poche difficoltà a capire la prova di cui sopra.
Se un bambino capisce veramente cos'è l'area, ne capisce la misura e capisce anche che l'area di qualsiasi figura può essere espressa attraverso le sue caratteristiche (in questo caso l'ipotenusa e l'angolo), che definiscono in modo unico la figura.
Ma non è una prova rigorosa.
Non posso farlo in modo intelligente, quindi lo farò in modo semplice:
Ecco perché abbiamo bisogno di una soluzione analitica generale, non per disegnare tali tabelle, ma per sostituire due valori di input in una semplice formula e ottenere la risposta.
Questo è il punto, tutto quanto sopra è "sembra che sia così che sarà". Che "può essere in qualche modo espresso attraverso qualcosa".
Ma non è una prova rigorosa.
Che razza di prova concreta è questa?! È ovvio: