[Archives] Mathématiques pures, physique, chimie, etc. : problèmes d'entraînement cérébral sans rapport avec le commerce. - page 614
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Dima, pourquoi veux-tu connaître la probabilité qui diffère de un par des millièmes de pour cent ? Si vous voulez des garanties, il n'y en a pas. Des lauréats du prix Nobel (LTCM) et Niederhoffer lui-même se sont cachés derrière des probabilités à un degré moins un - et ont quand même "frappé".
Et de très petites probabilités (très grandes) sont utilisées pour calculer la durée de vie approximative du système. Il est important de savoir combien de temps il durera - un an ou 10 ans.
Peut-on compter sur quelque chose ? Les mathématiques sont le meilleur moyen d'y parvenir.
N'est-ce pas ?
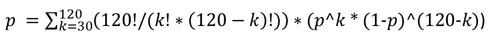
C'est ça !
Mais les erreurs d'arrondi peuvent gâcher toute la précision. Il est préférable de compter la somme de 0 à 30. Elle sera égale à l'addition à la probabilité que vous voulez connaître.
Il y a des cas, il y a des cas où la somme des visages est égale à 17.
Par exemple, (333332) > (662111), avec une probabilité de gagner de 23/36 ~ 0,64. Certes, ce n'est pas simple : (662111) ne gagne pas avec une marge appréciable.
Il semble que jusqu'à présent la somme des visages de 18 soit la plus fertile.
Si nous retournons les boules, alors c'est toujours p=q, donc nous pouvons simplifier la formule dans le côté droit (* p^120)
Cela n'a pas vraiment d'importance si nous revenons ou pas. Nous extrayons trop peu pour faire la différence. Mais on peut le simplifier décemment. Et dans les parenthèses avec des puissances, le multiplicateur (1/2)^120 restera.
Hehe.
2 Dima: Ne vous embêtez pas avec ces combinaisons. Maîtrisez la distribution normale et prenez une intégrale définie de zéro à la borne inférieure correspondant à votre 30. Vous ferez une grosse erreur avec les combinaisons dans cette formule, à moins que vous ne trouviez une formule analytique pour la simple somme des combinaisons.
Ou essayez la somme des combinaisons de 0 à 30, les notes p ne vous gêneront pas. Vous pourriez avoir de la chance.
P.S. En bref, c'est simple. Regardez ici.
Vous devez calculer k1, k2 et ensuite l'intégrale.
Prenons k1=0, k2=30, c'est plus précis. n=120, p=q=1/2. Puis
(k2-np)/sqrt(npq) = (30-60)/sqrt(120*1/2*1/2) ~ -5.477
(k1-np)/sqrt(npq) = (0-60)/sqrt(120*1/2*1/2) ~ -10.954.
De plus, 1/sqrt(2*pi) ~ 0.39894 est très utile.
Substituez les deux premiers nombres dans les limites d'intégration, et substituez 0.39894*exp(-x^2/2) dans la fonction intégrande, et nous obtenons (voici un service sur la prise de certaines intégrales) :
2.163*10^(-8).
Donc votre probabilité est de 1-2.163*10^(-8) ~ 0.99999998.
N'essayez même pas de prendre l'initiale de la fonction sous l'intégrale : elle est non-entière.