[Archives] Mathématiques pures, physique, chimie, etc. : problèmes d'entraînement cérébral sans rapport avec le commerce. - page 313
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
P.S. Вероятно, предполагается, что гири можно ставить только на одну чашку весов. На другой - груз.
Одно решение очевидно: 1, 2, 4, 8, 16, 32.
1,2,4,8,16,32 - réponse unique
Si un poids est inférieur à 2^n, le poids total sera inférieur à 63,
S'il y en a plus, il y aura des lacunes dans la séquence des poids que l'on peut obtenir avec ces kettlebells.
Il est intéressant de noter que le problème devient considérablement plus difficile et intéressant si les poids peuvent être placés sur les deux gobelets en même temps. C'est celui que j'aimerais torturer. Mais je ne connais pas la solution.
Bien que de toute façon il s'avère que le poids minimum des poids est 1. Mais cela ne signifie pas automatiquement qu'ils vont jusqu'au degré 2.
Suivant (10e) :
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
Je ne suis pas sûr du minimum de kettlebell 1
peut-être que deux kettlebells 2 et 3 fonctionneraient aussi.
Интересно, что задача становится существенно сложнее и интереснее, если гирьки можно ставить на обе чашки одновременно. Вот ее бы помучить. Но известного мне решения нет.
Хотя в любом случае получается, что гирька минимального веса - это 1. Но это не означает автоматически, что они идут степенью двойки.
L'ordinateur a fait le calcul :)
Si les poids peuvent être placés sur les deux tasses simultanément, le problème a 2136 solutions (exactement 63 poids peuvent être équilibrés).
En effet, toutes les solutions contiennent un poids de 1.
Компьютер подсчитал :)
Если гирьки можно ставить на обе чашки одновременно, то задача имеет 2136 решений (можно уравновесить ровно 63 груза).
Действительно все решения содержат гирьку с весом 1.
Allez-vous afficher le programme ? S'il vous plaît, s'il vous plaît !
Yep, demande en larmes un programme.
Доказательство того, что минимальная - 1, несложно: максимально возможный вес равен сумме всех шести чисел, а тот, что ближайший к нему, равен сумме пяти (шесть без минимальной гирьки). Разница между максимальным и ближайшим к нему весом должна быть равна 1. Следовательно, минимальная равна 1. ihor, доказано, надеюсь?
Ага, слезно просим программку.
J'avais tort sur 1.
Il n'y a rien d'intéressant dans le programme, un simple dépassement.
#include <stdio.h>
#define COUNT 63
bool isOK(int v0,int v1,int v2,int v3,int v4,int v5){
bool arr[COUNT] ;
for(int i=0;i<COUNT;i++) arr[i]=false ;
// 1 - sur une tasse, 0 - le poids n'est pas impliqué -1 - sur la deuxième tasse
for(int i0=-1;i0<=1;i0++)
for(int i1=-1;i1<=1;i1++)
for(int i2=-1;i2<=1;i2++)
for(int i3=-1;i3<=1;i3++)
for(int i4=-1;i4<=1;i4++)
for(int i5=-1;i5<=1;i5++) {
int ves=v0*i0+v1*i1+v2*i2+v3*i3+v4*i4+v5*i5;
if(ves > COUNT) return false ;
si(ves>0) arr[ves-1]=vrai ;
}
for(int i=0;i<COUNT;i++)
if(!arr[i]) return false ;
retourner vrai ;
}
main(){
for(int i0=1;i0<COUNT;i0++)
for(int i1=i0;i1<=COUNT-i0;i1++)
for(int i2=i1;i2<=COUNT-i0-i1;i2++)
for(int i3=i2;i3<=COUNT-i0-i1-i2;i3++)
for(int i4=i3;i4<=COUNT-i0-i1-i2-i3;i4++)
for(int i5=i4;i5<=COUNT-i0-i1-i2-i3-i4;i5++)
if(isOK(i0,i1,i2,i3,i4,i5))
printf("%d %d %d %d %d %d\n",i0,i1,i2,i3,i4,i5) ;
}
Следующая (10-й):
La preuve est sans grande rigueur, mais correcte.
Introduisons la notation des coordonnées des sommets, comme le montre la figure. Pour que le bleu soit un carré
x1-x2=y1-y4 ;
y1-y2=x1-x2 ;
ainsi que
x3-x4=y2-y3 ;
y4-y3=x2-x3.
A partir des deux premières équations, si on rappelle l'équation du graphique, on obtient
x4-x2=A(sinx2-sinx4),
des troisième et quatrième
x3-x1=A(sinx1-sinx3).
Puisque aucune restriction n'est imposée aux carrés autre que le nombre minimum de carrés, nous ne considérerons que les cas où les carrés sont symétriques par rapport à l'origine. Mais alors x4=-x2, x3=-x1 et pareil pour les sinus. Nos équations prendront la forme suivante :
sin(2*x2)/(2*x2)=1/A
sin(2*x1)/(2*x1)=1/A
Rappelez le graphique des fonctions de x2 et x1 se trouvant sur les côtés gauches. Pour ce faire, observez la figure : le graphique présente des extrema décroissants en x positif et négatif. Évidemment, en réduisant progressivement le nombre A, nous pouvons obtenir autant de racines que nécessaire, y compris 1978 et plus.
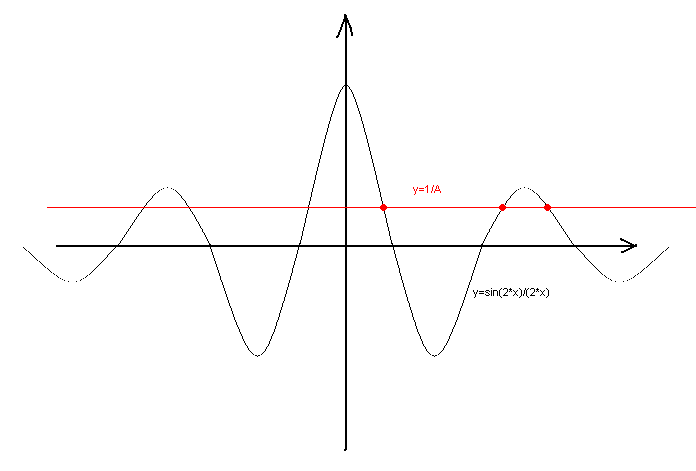
Les racines obtenues sont différentes et se rapportent les unes aux autres de manière purement irrationnelle. Je n'ai pas besoin de prouver en détail que les carrés dans ce cas ne sont pas égaux par paire.