L'étiquette du marché ou les bonnes manières dans un champ de mines - page 102
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Maintenant, parlons de son utilité (pertinence). Par construction, il s'agit toujours d'une série alternée. Que proposez-vous de rechercher dans ses motifs, le ratio des côtés en zigzag de Kagi ?
Les motifs eux-mêmes aussi, puisque.
La RT est une dérivée du kaga de construction, la RT elle-même est juste un nombre N - 1 sur chaque segment de kaga de N longueurs, est-ce que je comprends bien ?
Si oui, alors le PT doit aussi être alterné.
Si non, alors expliquez comment la construction correcte d'un cagi permet d'obtenir plusieurs PT de même signe dans un segment de cagi ?
Pour être précis, Pastukhov traite les motifs de kagi
et le tableau 3.1 parle des modèles kagi
Je propose d'utiliser les données primaires - les modèles kagi, et de construire des PTs basés sur leurs propriétés.
Donc je pense que c'est important :
Le PT est un dérivé du cagi de construction, le PT lui-même est juste un nombre N - 1 sur chaque segment de cagi de longueur N, est-ce que je comprends bien ?
Oui, c'est correct.
Si c'est le cas, alors le RT doit également être variable en fonction du signe. Dans la négative, expliquez comment il est possible d'obtenir plusieurs RT du même signe sur le même segment kagi si la construction du kagi est correcte ?
Non, ce n'est pas une affirmation correcte. Il suffit de réaliser une fois les constructions nécessaires pour s'en convaincre :
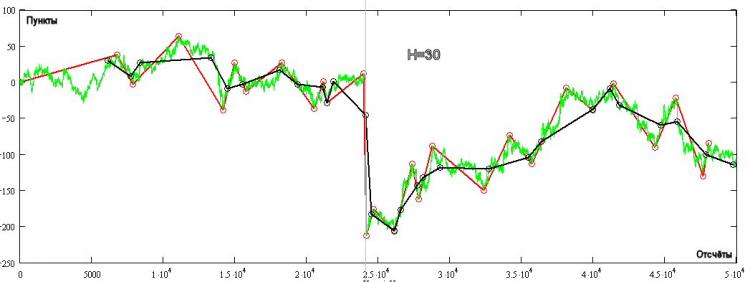
Dans la figure, le vert montre une cotation en tick, le rouge est la construction Kagi (toujours variable en signe) pour H=30 pips, et le noir est le PT. Il existe un certain nombre de domaines où PT n'est pas une variable de signe ! La manière dont cela se produit est visible dans le graphique même - la lecture du TP suivant est obtenue lorsque le prix s'éloigne du sommet d'une valeur supérieure ou égale à H. Le TP ne change pas en fonction de la stratégie que vous suivez (H+ ou H-), il dépend uniquement de la direction de la position ouverte à chaque lecture du TP.
Je propose d'utiliser des données primaires - des modèles de cagi, et de construire des PTs basés sur leurs propriétés.
C'est pourquoi je pense que c'est important :
Une contre-suggestion est de parvenir à un accord sur les questions majeures.
Par exemple, essayez d'obtenir un consensus sur la question des éventuels PT cognats, puis que pour la suite de la discussion, il suffit d'utiliser les PT uniquement, sans faire appel au modèle Kagi original. Et enfin, de convenir qu'il est nécessaire et suffisant d'utiliser la série RT en première différence pour l'analyse (même si Pastukhov ne le fait pas), ce qui simplifie sensiblement l'analyse des modèles !
Si vous, Michael, avez une vision différente de l'approche de ce problème, je serais heureux de lire les résultats de vos recherches.
Une contre-suggestion est de parvenir à un accord sur les principales questions.
Par exemple, pour tester un consensus sur un éventuel cognate PT, alors, que pour la suite de la discussion, nous devons utiliser uniquement PT, sans faire appel à la construction originale de Kagi. Et enfin, de convenir qu'il est nécessaire et suffisant d'utiliser la série RT en première différence pour l'analyse (même si Pastukhov ne le fait pas), ce qui simplifie sensiblement l'analyse des modèles !
Si vous, Michael, avez une vision différente de l'approche à adopter face à ce problème, je serais heureux de lire les résultats de vos recherches.
Une différence dans la définition de DH est révélée :
Comprenons votre définition.
En quoi diffère-t-elle d'une série Renko ?
Si ce n'est pas le cas, alors nous sommes confrontés à un choix de méthode de construction de modèle pour la prévision entre Kagi et Renko.
Aux pages 82-85, Pastukhov évalue la stabilité statistique de ces deux séries et arrive à la conclusion suivante
Il est assez logique de prendre les plus stables comme prédicteurs.
Quels sont vos arguments en faveur du choix de la construction renko comme prédicteurs ?
Je parle des constructions Kagi.
La différence entre Renko et Kagi selon la thèse, est que pour les constructions Renko, la distance entre les sommets du Renko-zigzag est toujours un multiple de H et est toujours supérieure ou égale à H. Pour Kagi, cette distance peut être quelconque et est toujours supérieure ou égale à H.
Michael, regarde l'image ci-dessus, pour les constructions Kagi (celles en rouge), la longueur du segment peut être de 3.14H, Sur la même section, Renko ne peut être que de 3H. C'est toute la différence !
Et je suis tout à fait d'accord avec vous pour dire qu'il n'y a pas de concurrence de Renko et qu'il n'y a aucun intérêt à envisager cette panne.
Je parle des constructions Kagi.
La différence entre Renko et Kagi selon la thèse, est que pour les constructions Renko, la distance entre les sommets du Renko-zigzag est toujours un multiple de H et est toujours supérieure ou égale à H. Pour Kagi, cette distance peut être quelconque et est toujours supérieure ou égale à H.
Michael, regarde l'image ci-dessus, pour les constructions Kagi (celles en rouge), la longueur du segment peut être de 3.14H, Sur la même section, Renko ne peut être que de 3H. C'est toute la différence !
Et je suis tout à fait d'accord avec vous pour dire qu'il n'y a pas de concurrence pour Renko et qu'il n'y a aucun intérêt à envisager cette scission.
Reprenons lentement et simplement :
Sans demander "quel est le nom de la fonction PT monotone par morceaux qui en résulte ?".
Posons-nous les questions :
J'ai une réponse approximative à la première question : il s'agit d'une sorte de MA, c'est-à-dire d'une tentative de moyenne d'une série chronologique de prix.
J'espère que vous serez d'accord avec cela.
La deuxième question est alors la suivante : pourquoi est-il meilleur comme prédicteur qu'un MA quantifié en N ?
est une sorte de MA, c'est-à-dire une tentative de moyenne de la série chronologique des prix.
J'espère que vous êtes d'accord avec cela.
Oui, je le fais.
La deuxième question est alors : quelle est sa supériorité en tant que prédicteur de la même AM quantifiée N ?
Mashka, indépendamment des modèles cachés de BP lissés, aura un FP constant. Si nous introduisons quelque chose de similaire à la PF pour la RT, un phénomène intéressant est observé, à savoir que plus la PF est différente d'un processus de Wiener, moins la PF aura la RT. C'est-à-dire que le décalage maximal du PT est observé sur un processus aléatoire intégré et, quantitativement, le PT ne présente pas la propriété de variabilité de signe. Cependant, dès que le marché devient arbitraire, le PT présente des propriétés de signe-variance et son "retard" diminue.
En d'autres termes, l'effet de "lissage" pour le PT n'est observé qu'à un tel H, où le marché est exempt d'arbitrage (la valeur moyenne du segment Kagi tend vers 2H) et cela peut servir de signal pour passer à d'autres horizons de négociation par le paramètre H. Ou, trouver le moyen d'exploiter cette régularité.
Expliquez-moi s'il vous plaît, je travaille dans la finance depuis je ne sais combien de temps et le terme transaction a toujours été utilisé.
Et maintenant je regarde sur wikipedia, soi-disant dans la banque c'est une transaction. C'est très étrange, la liposuccion...
Qui peut commenter ?
Alors allez-y et corrigez-la vous-même sur cette WikiPedia.
Je pense que la transaction est plus correcte, aussi.
En d'autres termes, l'effet de "lissage" pour PT n'est observé que sur un tel H, où le marché est sans arbitrage (les segments moyens de Kagi tendent vers 2H), et cela peut servir de signal pour passer à d'autres horizons de négociation par le paramètre H. Ou bien, trouver un moyen d'exploiter ce schéma.
Serge, je m'abstiendrai pour l'instant de toute comparaison avec d'autres constructions et approches (je dois aller jusqu'au bout du sujet),
On y reviendra peut-être plus tard. Pour l'instant, sur le sujet du kagi :
Puisque la volatilité de H dépend du choix de H, deux mesures supplémentaires sont nécessaires pour une analyse kagi complète.
1) Un graphique de la volatilité de H en fonction de H. (Horizontal H, vertical H-volatilité)
2) Un graphique de la volatilité de la H-volatilité elle-même. En termes simples - un graphique de la volatilité H en fonction de
temps (pour H fixe). Vous ne pouvez pas vous en passer. Si la courbure est trop forte, il n'y a rien à attraper dans ces parties.
Pourquoi n'essayez-vous pas de faire un tracé tridimensionnel (x=t, y=H, z=HVol) ?
2) Un graphique de volatilité de la H-volatilité elle-même. En termes plus simples, un graphique de la volatilité H en fonction de
temps (pour un H fixe). Vous ne pouvez pas vous en passer. Si la courbure est trop forte, il n'y a rien à attraper dans ces parties.
Je vais essayer d'exposer ma compréhension de la situation.
Pour évaluer les perspectives de négociation d'un instrument, vous devez disposer d'une estimation quantitative de la prévisibilité.
En d'autres termes, nous travaillons avec
pour un instrument spécifique si (et jusqu'à ce que) il existe au moins un signe de H-volatilité pour lequel H-volatilité
est prévisible au moment de la transaction (tT), qui dépend à son tour de la sélection de Н.
C'est-à-dire qu'un tableau bidimensionnel est de toute façon nécessaire (les valeurs dans les cellules sont de la troisième dimension). La diffusion n'a pas d'importance pour le moment.
En parlant de kagi :
Puisque la volatilité de H dépend du choix de H, deux mesures supplémentaires sont nécessaires pour une analyse kagi complète.
1) Un graphique de la volatilité de H en fonction de H. (Horizontal H, vertical H-volatilité)
C'est ici :
J'ai joint ci-dessous un fichier au format texte contenant des lignes de transactions.
Le format du fichier est le suivant :