Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
¡Saludos, Vladimir!
No hay ninguna obra suya sobre física cuántica en Internet; he buscado de todo. Sólo queda la basura, escrita en su vejez. Realmente quiero entender cómo llegó a esta ecuación pseudo-diferencial... No te lo vas a creer: sus conclusiones analíticas coinciden plenamente con mis datos experimentales.
En https://www.mql5.com/ru/forum/221552/page158#commen t_6392311 te he dado el enlace.
Contiene el parámetro (Overshot), los programas MQL que lo calculan, las formas de aplicarlo e interpretar los resultados - en general, todo lo que no tiene la no entropía. Y, lo que es más importante, una prueba directa de la separación de la tendencia del plano. A diferencia de la no entropía, en cuyas propiedades necesarias estamos hasta ahora convencidos por su tradicional "tal y cual", cuyo precio ya ha sido aclarado aquí por numerosos ejemplos de su convicción, la certeza. Incluyendo los absolutos.
Poner un monumento a los autores de ese mensaje (artículo).
La tendencia del piso está muy bien separada por la habitual actualización de máximos y mínimos, si acaso (muy cercana en su significado a los overshots de los que escribe Vladimir. Es cierto que el zigzag tiene un umbral fijo, y no me gusta mucho).
Me gustaría aclarar.
Creo que es interesante ver el efecto de la naturaleza de las fluctuaciones en la rentabilidad de la negociación en la ruptura del nivel y en el rebote del nivel. De ahí la división tendencia/flotación y su finalidad. En http://www.argolab.net/izuchaem-zigzagi.html se refleja directamente este objetivo:
"Si en la práctica el valor medio de los overshots es mucho mayor que 1, significa que es rentable abrir una operación hacia la dirección de una rodilla formada en ZigZag ("to breakout"). Y si es significativamente menor que 1, entonces deberíamos abrir una operación en la dirección opuesta ("on reversal")".
Todavía no entiendo cómo se refleja este objetivo en la "actualización normal de hai/loi". ¿Me lo dirías?
Es sólo una herramienta, como el zigzag, por ejemplo: Alto(i, 30)-Alto(i+5, 30). Simplemente me resulta más cercano porque (probablemente) tiene en cuenta mejor la volatilidad actual. Como en el zigzag, es posible inventar algunas métricas, por ejemplo, dividir el valor de actualización por la altura (¿anchura?) del canal. En un plano será cercano a cero, en una tendencia será de 0,5-1. Cuando el zigzag tiene un exceso, este instrumento tendrá una actualización alta/baja.
En cuanto a la naturaleza de las fluctuaciones, promediar las métricas sobre todo el activo es algo así como la "temperatura media del hospital", porque la tendencia/planeza se concentra en ciertas horas del día (si hablamos de trabajo intradiario). Aunque hay dos cruces (creo que sabes cuáles) que tienen, de media, una planitud ligeramente superior a la de otros pares.
Se trata de un parámetro que permite distinguir entre un piso y una tendencia.
Este parámetro no es el coeficiente de Hearst.
¿Sabes qué? Este parámetro se llama la no-entropía https://en.wikipedia.org/wiki/Negentropy.
El primero que aprenda a calcularlo correctamente y a utilizarlo en algoritmos, debería recibir en vida un monumento de la humanidad agradecida. ¡Eso es!
otro intento de suavizar
Se puede hacer así
Pero sólo hay un problema.
de nuevo, pierde precisión.
Y "un centavo ahorra un centavo".
otro intento de suavizar
Eso está bien.
pero sólo hay un problema.
Una vez más, se pierde la precisión.
y "un centavo salvó un centavo".
No, es algo genial. De hecho, es la suma de los productos de las probabilidades de los incrementos y los logaritmos de esas probabilidades para un tamaño de muestra determinado. Muestra en qué medida la distribución de probabilidad en un momento dado difiere de algún punto de referencia. Sólo tienes que hacer una tabla, como Hurst, y ya está.
Llevo mucho tiempo buscando este parámetro oculto, ya que la asimetría y la curtosis no son suficientes. Pedí con lágrimas en los ojos a los comerciantes de este foro que me ayudaran a encontrarlo. Sólo 2 operadores que respeto - Vladimir y Dmitriy Skub - respondieron a esta solicitud. Ambos sugirieron sus variantes. No he entendido nada y no entiendo nada. ¿Cómo es que la gente gana dinero aquí sin saber nada? Es una paradoja.
Aquí están los gráficos para AUDCAD durante las últimas 2 semanas con un tamaño de muestra de 16900 ticks para el tiempo de lectura exponencial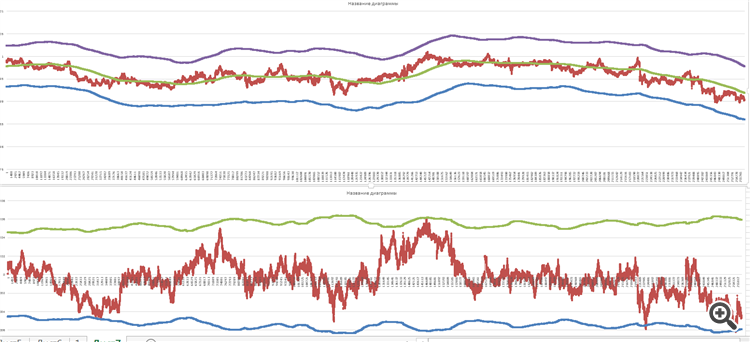
Sí, todo parece estar bien, pero hay algo que me preocupa... Déjame explicarte qué.
Primero, un poco de teoría:
Este producto F(x,t) es la distribución de incrementos que vemos.
La función de MacDonald es responsable de la "memoria" de nuestro proceso.
Y esto es lo que obtengo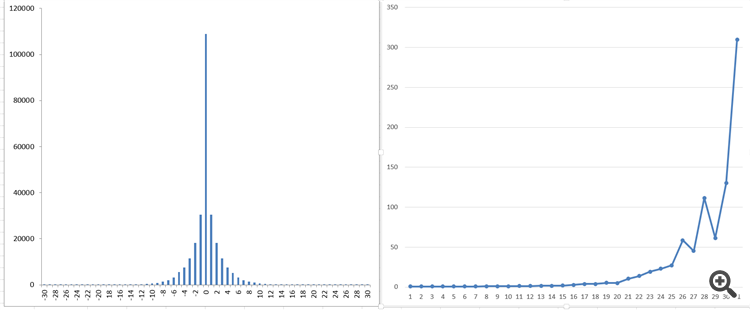
Lo que ves a la derecha es lo que obtengo como "memoria" del proceso.
¡Esto es con una población general de más de 250.000 garrapatas!
Por desgracia, no veo una función suave como las funciones de Bessel modificadas. No debería haber estos "saltos"...
Por este motivo, casi he llegado a la conclusión de que, después de todo, probablemente esté tomando los datos de las garrapatas de forma equivocada.
Todavía tengo que tomarlo a intervalos regulares. Aunque... Sólo la práctica puede confirmarlo.
Hasta ahora me he quedado con un buen resultado y con unas dudas desmesuradas...
Y esto es lo que consigo.
Lo que ves a la derecha es lo que obtengo como "memoria" del proceso.
¡Esto es con una población general de más de 250.000 garrapatas!
Por desgracia, no veo una función suave como las funciones de Bessel modificadas. No debería haber estos "saltos"...
Por esta razón, casi he llegado a la conclusión de que, después de todo, probablemente esté tomando los datos de las garrapatas de forma equivocada.
Todavía tengo que tomarlo a intervalos regulares. Aunque... Sólo la práctica puede confirmarlo.
Hasta ahora me he quedado con un buen resultado y con dudas sin resolver...
Sus datos son correctos: todo el mundo los tiene, y en todos los plazos. Es el tipo habitual de incrementos inestables con un ramillete completo: cambios de media, cambios de varianza, colas y efecto ARCH. Hay que modelar todo:
Y miles y miles de personas han estado haciendo esto durante 30 o 40 años.