[Archivo] Matemáticas puras, física, química, etc.: problemas de entrenamiento cerebral no relacionados con el comercio de ninguna manera - página 614
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Dima, ¿por qué quieres saber la probabilidad que difiere de uno en milésimas de porcentaje? Si quieres garantías, no las hay. Los premios Nobel (LTCM) y el propio Niederhoffer se escondieron detrás de las probabilidades en algún grado menos uno, y aun así "acertaron".
Y las probabilidades muy pequeñas (muy grandes) se utilizan para calcular la vida útil aproximada del sistema. Es importante saber cuánto durará: un año o 10 años.
¿Hay algo en lo que confiar? Las matemáticas son el mejor camino.
¿Verdad?
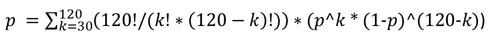
¡Eso es!
Pero los errores de redondeo pueden acabar con toda la precisión. Es mejor contar la suma de 0 a 30. Será igual a la adición a la probabilidad que quieres conocer.
Hay casos, hay casos en los que la suma de las caras es igual a 17.
Por ejemplo, (333332) > (662111), con una probabilidad de ganar de 23/36 ~ 0,64. Es cierto que no es sencillo: (662111) no gana por un margen apreciable.
Parece que hasta ahora la suma de las caras de 18 es la más fértil.
Si devolvemos las bolas, entonces siempre es p=q, por lo que podemos simplificar la fórmula en el lado derecho (* p^120)
Realmente no importa si volvemos o no. Extraemos muy poco para hacer la diferencia. Pero se puede simplificar decentemente. Y en los paréntesis con potencias quedará el multiplicador (1/2)^120.
Jeje.
2 Dima: No te molestes con estas combinaciones. Hazte con la distribución normal y toma una integral definida desde cero hasta el límite inferior correspondiente a tu 30. En esta fórmula cometerás un gran error con las combinaciones, a menos que encuentres una fórmula analítica para la suma simple de combinaciones.
O prueba la suma de combinaciones de 0 a 30, las notas p no te molestarán. Puede que tengas suerte.
P.D. En resumen, es sencillo. Mira aquí.
Hay que calcular k1, k2 y luego la integral.
Tomemos k1=0, k2=30, esto es más preciso. n=120, p=q=1/2. Entonces
(k2-np)/cuadrado(npq) = (30-60)/cuadrado(120*1/2*1/2) ~ -5,477
(k1-np)/cuadrado(npq) = (0-60)/cuadrado(120*1/2*1/2) ~ -10,954.
También 1/sqrt(2*pi) ~ 0,39894 viene bien.
Sustituyendo los dos primeros números en los límites de integración, y sustituyendo 0,39894*exp(-x^2/2) en la función integrante, obtenemos (aquí hay un servicio sobre la toma de ciertas integrales):
2.163*10^(-8).
Así que su probabilidad es 1-2,163*10^(-8) ~ 0,99999998.
Ni siquiera intentes tomar la inicial de la función bajo la integral: es no entera.