Vista del Análisis Técnico en el contexto de Sistemas de Control Automáticos (SCA), o "Vista inversa".

Introducción

Para ganarse la vida, basta con trabajar.
Sin embargo, para ser rico, hay que encontrar algo más.
Alphonse Karr
(traducido del francés por MetaQuotes Software Corp.)

Si algo sale mal, hay que mejorar, expandir horizontes, mirar a las cosas de forma diferente. A veces esto puede darte resultados interesantes e inusuales. A primera vista, algunas ideas parecen absurdas... "por definición". Afortunadamente, es sólo a primera vista. De hecho, una persona que no esté preparada no puede imaginarse lo que pasa con, por ejemplo, las velocidades relativistas. La escala es, por supuesto, completamente diferente, pero alguien discutirá a veces los extremos teniendo sus aplicaciones prácticas. Los resultados más interesantes e inusuales se obtienen a menudo utilizando algo "inusual". Lo que se trata aquí es exactamente ese "algo".

El análisis técnico se ha desarrollado durante muchos años. El entendimiento de este proceso es cada vez más profundo, y se utilizan propiedades y leyes cada vez más complicadas. Y, lo que es más notable, hace ya bastante tiempo que se empezó a hablar sobre los sistemas de trading completamente automatizados. Al mismo tiempo, la teoría y la práctica del control automático continúan desarrollándose como asunto científico e ingeniero.

Es lógico que la educación y las experiencias en estos dos campos sugieran la idea de mezclarlos. La sensación constante de superficialidad, y el deseo de golpear la naturaleza del caso son estímulos adicionales. Los métodos más conocidos, por muy complicados que sean, utilizan propiedades más bien simples.

A continuación hay una breve representación del desarrollo de año y medio en esta dirección. Son principalmente teoría y algunos métodos prácticos interesantes. Todo es de "eficacia probada". La intención era representar una vista alternativa. Puedo proporcionar más detalles más tarde si es necesario.

Es interesante que resultó ser una generalización de las leyes que ya existían, pero a veces es una "vista inversa" de verdad. Por supuesto, se puede decir que el tema es que las máquinas y las finanzas con "peras y manzanas". Sin embargo, creo que aún así tienen mucho en común. Es más, en lo que respecta al lado técnico, la teoría en sí está desarrollada de forma mucho más fundamental, es decir, no como una aplicación en un sólo campo, si no mucho más profunda. Unas leyes así son siempre más fiables. Naturalmente, los principios de alto nivel pueden encontrar sus aplicaciones aquí. En el ámbito técnico, la discretización y expansión son más bien desagradables. El principio principal de control es bastante inusual. La cuestión son las leyes fundamentales exactas.

En mi opinión, resultó ser una generalización de los principios conocidos en una clase más grande de sistemas y profundizando en la parte de la misma que no se ha tratado tradicionalmente con anterioridad (al menos en mi práctica). Esto, por supuesto, no reduce la importancia de los métodos clásicos.

Principios centrales

Nadie debería creerse Dios o Su profeta.
Es suficiente con escuchar a una persona que te hace pensar.
Atribuido a Peter Oppenheimer

Visto tradicionalmente, el análisis resuelve la tarea de predecir y encontrar los puntos de entrada/salida del mercado. Cuando se abre una posición, está acompañada (protegida, etc.). Incluso esta fórmula en sí implica una discretización alta y la existencia de movimientos "buenos" y "malos". El tema principal del análisis es el pasado, y hay alguna persistencia en la toma de decisiones.

Lo que pasará en el mercado, en el caso de que el "Santo Grial" se encuentre y se aplique en todo el mundo, es otro tema.

Los movimientos del mercado y su utilidad están relacionados generalmente de una forma muy simple. Por ejemplo, el viernes 8 de agosto de 2008, el precio de los valores más líquidos cayó en el mercado de valores ruso en un fondo negativo externo. Los inversores están incómodos.

Además, el análisis y la toma de decisiones representan a menudo dos sistemas separados. Un analista estima la situación del mercado y propone sus recomendaciones. Todo el control se reduce a comparar los datos analíticos de varias fuentes (incluidas as de uno mismo), tomar la decisión de abrir o cerrar, y acompañar la posición en base a la información obtenida. No se prevén respuestas, o está mal realizado debido a que la información sobre la situación del trader parece ser absurda para el analista. Además, la parte analítica está distribuida y puede cambiarse.

Las construcciones creadas (indicadores, formas, etc.), como norma general, están muy relacionadas con las leyes fundamentales del mercado. Normalmente, están relacionadas sólo con las leyes del mercado (psiologíca, macroeconomía, etc.). Hay algunos métodos más generales, como Fibonacci o Elliot. Sin embargo, muchas otras leyes fundamentales participan en el trabajo de un SCA (sistema de control automático).

Todo lo anterior es un caso especial. Puede que todo vaya por opuestos.

El análisis técnico en sí no es un campo simple, mientras que una parte del mismo (control) es incluso más complicado. Esto es, en parte, porque necesita conocimientos profundos y experiencia en muchos campos técnicos (dinámicas no lineales, matemáticas computacionales, análisis de sistemas, teoría de probabilidad, y estadísticas matemáticas, programación, etc.) y en el campo de mercados financieros, análisis de inversiones, etc. Sin embargo, el precio también es mucho más atractivo.

Por lo tanto, el control puede ser prácticamente permanente (discreto, por supuesto, pero "siempre en el mercado"). Otro tema es que la actividad puede ser baja la mayoría del tiempo. La relación entre los movimientos de mercado y su utilidad puede resultar complicada, altamente no lineal. Es un algo opcional que los movimientos "buenos" y "malos" (para el sistema) del mercado se determinan por procesos psicológicos o macroeconómicos (podrá ver un ejemplo más abajo). Puede haber muchas respuestas, cuando la identificación del estado incluye considerar los datos sobre los resultados obtenidos.

En la teoría del control automático, el sistema de tipo servo es estándar, es decir, un sistema que sigue de cerca la tarea. La diferencia entre la tarea y el resultado actual se introduce en el sistema de control. Sería absurdo utilizar esto (tal como es) en el mercado. Sin embargo, la idea en sí se puede aplicar aquí también.

Así que, considerándolo desde este punto de vista, el análisis está relacionado permanentemente con el control. Sería más apropiado hablar sobre el control que incluye análisis. Además, un sistema se entiende, en conjunto, como un objeto de control, un sistema de control y comunicaciones. Un objeto se entiende, por supuesto, como una cuenta, pero esto se realiza a través de mercado, aumentando posiciones. El control de las tasas y los precios (por ejemplo, el cambio de tasas de un país o varios países, los precios de los valores de una compañía, o sus competidores, etc.) es otro tema.

E rol del análisis, que consiste en la predicción, no es tan importante en este contexto, y desaparece por completo en los casos extremos. Luego la tarea principal es responder a la pregunta: ¿Qué se debería hacer en diferentes variaciones de desarrollo y qué puede resultar?
Esta abstracción resulta en el uso de otras propiedades del mercado.

Generalización y expansión

Tu propio Universo se crea conforme lo vas aceptando.
Winston Churchill

La ecuación básica se puede formular así:

y(i+1)=y(i) + (x(i+1) – x(i))*k(i)

en la que:

y: resultado,
x: gráfico inicial,
i: paso.

Está bastante claro. En el momento de "i", la posición está abierta con la cantidad de lotes igual a k(i). Más adelante, el resultado cambia en proporción a eso. Todavía no he considerado la expansión. También se puede escribir así:

dy(i)=dx(i)*k(i)

k(i) también tiene el sentido de velocidad. De hecho, puede haber varias opciones para k(i).

Podría parecer: ¿Qué más se puede inventar? Por ejemplo, esta ecuación es sólo una transformación de un gráfico a otro. El gráfico resultante es normalmente tomado como equidad (de nuevo, aquí no se considera la expansión). Esto no es necesario. Para una posición abierta, el gráfico resultante repite el inicial como el ponderado, es decir, sus propiedades pueden prácticamente corresponderse unas a otras. Se puede coger el gráfico obtenido como el inicial y procesarlo otra vez. De este modo, este sistema puede ser multinivel, mientras que la expansión se considera sólo en el último nivel. En cada nivel, debería mantener y añadir las propiedades necesarias y eliminar las que no lo son.

Si se prueba una idea o un sistema de trading y el resultado de la prueba no es satisfactorio (retrocesos grandes, beneficios inestables, etc.), se puede intentar mejorar el sistema. Sin embargo, este gráfico puede ser mejor que el inicial y puede merecer la pena procesarlo a un nivel más alto. No es el caso, por supuesto, pero puede pasar a menudo.

Recientemente he concebido la idea de que sería posible trabajar en la equidad de otros gráficos de forma similar. Esto abre una variedad de oportunidades interesantes. Sin embargo, este tema está muy relacionado con el desarrollo del mercado de inversiones, control de confianza, etc. Y bueno, eso es otro tema.

Esto era una complicación vertical, o consideración profunda. También es posible considerar todo horizontalmente, si utilizamos sistemas paralelos. En el caso más simple, este sistema compensa los inconvenientes del otro. La idea no es nueva. Es otro tema si están relacionadas. Entre otras cosas, estos sistemas deben sincronizarse debido a la presencia de descretización y expansión. Esto se considerará en el final de este artículo.
En un caso general, la ecuación principal se transforma en una ecuación combinada:

dy1(i)=dx(i)*k10(i)+dy1(i)*k11(i)+dy2(i)*k12(i)+…
dy2(i)=dx(i)*k20(i)+dy1(i)*k21(i)+dy2(i)*k22(i)+…
...

En mi práctica, había más de mil sistemas horizontales y más de diez niveles verticales.

Verticalmente, el sistema real es sólo el último sistema (tamaño de posición o velocidad multiplicadas en todos los niveles). Horizontalmente, cualquier sistema puede ser real. Quiere decir que algunos sistemas se pueden utilizar como auxiliares internos de los sistemas falsos. Ofrecen mucha más flexibilidad. Las propiedades aparecen, por ejemplo, cuando un sistema así actúa bajo las leyes de uno real, pero con una pequeña desviación, y está presente activamente en el funcionamiento de otros sistemas a mismo tiempo. Por ejemplo, si hay un sistema real que lo controla.

Finalmente, se añaden (o sustraen) los sistemas paralelos, para que todo se pueda reducir a la primera ecuación básica.

Si se añaden dos sistemas y si se sustrae una parte del resultado del primer sistema y se añade esa parte al resultado del segundo sistema, a suma seguirá siendo la misma y una operación así es bastante factible. A primera vista, no hay motivo para hacer esto, quizás sólo si no hay respuestas. Sin embargo, si la siguiente conducta del sistema depende de la situación actual, este método puede resultar el más adecuado (podrá ver un ejemplo más abajo).

Ahora unas cuantas palabras en cuanto a las transformaciones de los gráficos. Si el gráfico se mueve hacia arriba, está bien. Si se mueve hacia abajo, siempre se puede cambiar y volver a moverlo hacia arriba. Se puede disminuir fácilmente el depósito utilizando sólo la expansión o la carencia del depósito, aunque también pueden existir otras formas. O la tarea se reduce a eso de aumentar el depósito.

Si el gráfico está fluctuando, a menudo es posible convertirlo en un movimiento direccional. Depende de la propiedad del movimiento. Me gusta más reducirlo a esa forma primero y luego trabajar con él.

Estas son las tendencias conocidas y los mercados casi llanos. En la práctica, naturalmente, todo es más complicado: hay muchas frecuencias, incluidas las bajas.

Una característica útil: Cualquier gráfico se puede reducir a uno o dos formas. Otro tema es que las propiedades que se obtengan pueden no ser muy atractivas: El movimiento de tendencias puede tener retrocesos cortos pero largos, mientras que el movimiento fluctuante puede tener a veces una gran amplitud aleatoria. Pero estos inconvenientes aparecen si utiliza un método de fuerza bruta. Sin embargo, esta oportunidad, como tal, es útil.

Otra nota útil es que no hay ninguna limitación relacionada con la expansión o la escasez de depósito en los gráficos intermediarios, internos.
El mercado lleva una gran parte de incertidumbre en sí. Esta incertidumbre normalmente también pasa a la equidad debido a los métodos utilizados y a la cercanía de los gráficos inicial y resultante (un nivel). El significado de todas estas transformaciones consiste en que se cambian las propiedades de los gráficos consecutivamente en cada nivel para reducir la incertidumbre.

Algunas técnicas

Quién sabe cuántas palabras probó Dios, antes de encontrar la que podía crear el mundo.
Atribuido a Sanislaw Jerzy Lec

Todas las técnicas aquí descritas son sólo posibles herramientas que no pueden trabajar de forma independiente, pero pueden aplicarse en varias combinaciones con los sistemas compuestas de cada una. Están escritas como ejemplos que representan casos extremos. Sin embargo, puede haber mucho más entre extremos.

Sistemas de tipo servo

Se ha vuelto a examinar las respuestas estrictas. El ejemplo más simple (la solución no depende en el movimiento del gráfico inicial):

dy(i)=dx(i)*(y - g)*m

en el que:

m: coeficiente, una constante en este ejemplo;
g: tarea que puede ser una constante, pero también puede ser una variable.

Por otro lado, g es un atractor (uno simple, aunque también puede haber complicados), es decir, es un estado en el que el sistema es atraído por la tendencia a la baja o por el mercado llano. También es el punto de una posible bifurcación, es decir, de direcciones de movimientos multiplicadas más adelante, si no permitimos que el sistema se mantenga en este punto. Si el gráfico se mueve hacia arriba, el sistema tiende a dejar su estado estable en dirección a la posición en la que estaba el gráfico resultante cuando empezó a moverse.

Puede haber muchas variaciones.

Si g es una constante, el sistema es atraído a esta posición, y sólo las medidas específicas pueden sacarlo de ahí. Por ejemplo, el intercambio con otros sistemas (este es un ejemplo de por qué puede ser necesario), configurándolo como una curva sinuosa con una amplitud pequeña o de la siguiente manera:

dy(i)=dx(i)*(y - g)*m

en el que:
c: alguna constante.

Si c es positivo, no hay estados de equilibrio; si es negativa, hay dos: por encima y por debajo de cero. No se puede crear un sistema de oscilación con una amplitud limitada utilizando la "c" negativa, a causa de quedarse en las barreras. Cuando c es un número positivo, la amplitud no se limita y a menudo resulta ser muy grande. Sin embargo, todo esto depende de en qué esté trabajando el sistema en cuestión y qué técnicas adicionales se utilicen. Sin embargo, como totalidad, la situación es como se ha descrito arriba.

Todo esto se aplica a un amplio rango de sistemas de tipo servo, a la parte oscilatoria. Su apariencia estándar es más o menos así:

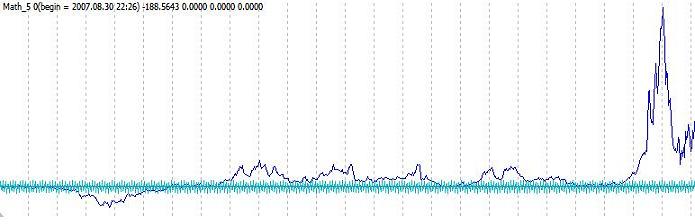
Otro ejemplo en el que la tarea no es una constante y, por ejemplo, se mueve linealmente. Entonces el sistema sigue la tarea la mayor parte del tiempo, nunca la excede, pero tiene retrocesos muy grandes. Si se colocan TakeProfit y StopLoss, la dirección del resultado a largo plazo depende en la volatilidad y en las tendencias. En cualquier caso, si se hace una inversa, no se obtendrá una técnica que limite el retroceso. Apariencia estándar:

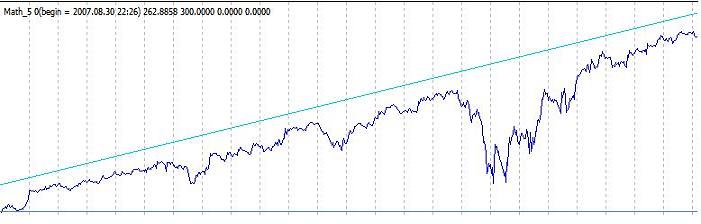
Esta tarea puede seleccionarse de una forma más complicada. Se puede coger, por ejemplo, el gráfico inicial en sí o el gráfico de otro sistema. Luego el resultado sigue bastante bien la tarea. Si se encuentran diferencias entre el gráfico inicial y el resultado, se obtendrá un sistema oscilatorio más. Hay muchas variedades aquí también.

Podría ser una buena dirección de trabajo: Deje que la tarea se mueva linealmente. Luego se pueden utilizar varias técnicas (por ejemplo, intercambio entre el gráfico iniciar y los que lo siguen) para intentar aumentar la probabilidad del movimiento desde la tarea. La mayoría del tiempo, el sistema se mueve exclusivamente en una dirección, pero se compensa con movimientos opuestos, raros pero fuertes. El problema es sólo que son raros. Luego se pueden intentar crear varios sistemas paralelos de este tipo, basados en los diferentes gráficos iniciales (otros pares de divisas, preprocesamientoss diferentes o por la técnica descrita abajo en procesos aleatorios). Se deberían añadir la sincronización para compensar los retrocesos y extensiones.

La limitación de retroceso puede ser una propiedad muy útil.

Otra solución sería utilizar dos o más sistemas prácticamente idénticos. Todos trabajarán bajo las mismas leyes, pero con pequeñas diferencias en la forma de introducir una señal aleatoria, por ejemplo, por la velocidad. Los sistemas deben tender al mismo valor. Luego, en el área de tarea, las diferencias entre ellos tiende a cero. Sustrayendo un sistema del otro, se puede obtener el resultado de introducir la señal aleatoria. No resulta muy aleatoria, pero la idea en su totalidad no es mala.

Los sistemas de tipo servo se pueden utilizar para el propósito opuesto, configurando con la tarea un límite que el sistema no debe sobrepasar. Luego, si se ha protegido contra la adhesión, el sistema oscilará sólo en un lado de la tarea.

Intercambio de datos

Volvamos a una variación simple. Si le añadimos un menos:

dy(i)=-dx(i)*(y - g)*m,

no se obtendrá ningún gráfico opuesto. Sólo se reemplazarán las acciones de las tendencias unas a otras. El primer sistema (con más) debe ser diferente a cero, el otro se le acercará, y viceversa. El mercado llano actuará de la misma forma.

Se puede complicar un poco. Vamos a añadir este intercambio de datos:

dy1(i)=dx(i)*(k1*y1 + k2*y2 – g)*m,
dy(i)=-dx(i)*(k2*y1 + k1*y2 – g)*m,

Si k1 = 1 y k2 = 0, se obtienen dos sistemas considerados por separado.

Si k1 > 0,5 y k2 < 0,5, los sistemas convergen también, pero un poco más lento (correspondientemente, la amplitud de la oscilación es más pequeña).

Si k1 = 0,5 y k2 = 0,5, se obtienen dos sistemas con oscilaciones propias analógicas. La velocidad depende de g. Si g es sinuosa, la velocidad también lo será. No debe oscilar sobre cero.

Si k1 < 0,5 y k2 > 0,5, el sistema se desvía. Sigue oscilando sobre cero, pero su amplitud aumenta con la aceleración (lo más probable, también con derivados más altos). Es decir, si la proporción entre las amplitudes de oscilaciones vecinas pudiera ser mayor que una al principio, se cuenta más tarde por cienes. Su apariencia típica (el sistema consiste en dos subsistemas, como se ve en la fórmula):

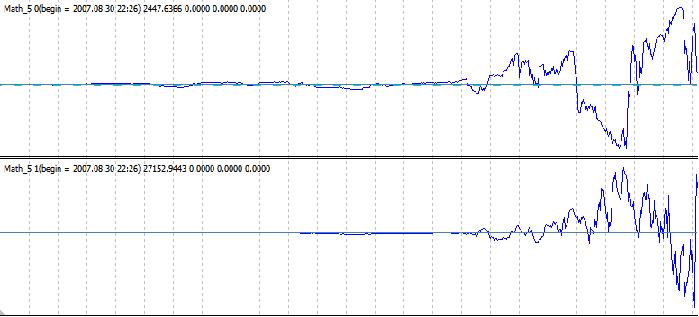
Para empezar, puede utilizar una sinuosa como tarea, pero es sólo razonable al principio. Simplemente puede configurar el valor inicial del resultado de uno de los sistemas diferente a cero. Ya no se desviará más: la situación de (y1=0, y2=0) se evita automáticamente.
En el movimiento en sí hay otras propiedades útiles.

Las ventajas principales son la oscilación sobre cero y la desviación.

El hecho de la inestabilidad en sí (la proporción entre las amplitudes es más de una) puede ser útil. Además, mire la primera ecuación básica. Es muy interesante que una transformación tan simple (con k1 y k2) cambie el gráfico tan considerablemente.

Por supuesto, este movimiento es muy complicado y apenas controlable. Aquí se puede hablar del arte del control. He hecho ciertos avances en los procesos así, pero las cosas no han llegado todavía a los sistemas reales.

Transformación retrógrada

Si es posible una transformación progresiva, también es posible una retrógrada (con estas condiciones):

dy(i)=dx(i)*k(i),
dx(i)=dy(i)/k(i).

Primero se puede hacer una progresiva (por ejemplo, la variación oscilante), corregirla utilizando una transformación más, y luego aplicar la transformación retrógrada al gráfico nuevo como en la anterior. Luego se obtendrá un gráfico inicial en la dirección que se necesita.

Se debería repetir que la mayoría de estas transformaciones son internas. Quiere decir que, finalmente, no pasará ningún gran retroceso o velocidad imprudente. Un gráfico desviado se puede limitar por dos niveles por encima y por debajo de cero. Oscilará y finalmente llegará a uno de ellos. No tiene mucho sentido como ta, pero sirve como ejemplo de limitación. A primera vista, dentro puede ocurrir un proceso extraño e inusual, pero no fuera. Es como un misil balístico que despegó de la Tierra y aterrizó en la Tierra, y utilizó las ventajas de su distancia de la Tierra en el camino.

Procesos aleatorios

Por cierto, hablando del espacio. Se puede abstraer incluso más del mercado utilizando procesos aleatorios, sin perder la generalidad. La primera transformación aparecerá de la siguiente manera:

dy(i)=dx(i)*k(i)

donde
k(i) - un (pseudo) número aleatorio. Por ejemplo, de -1 a 1. Prefiero utilizar una variación discreta: 1 o -1.

Sólo resulta la inestabilidad. Prácticamente todo lo demás es aleatorio. También pasan algunas propiedades del gráfico inicial en los periodos entre la toma de decisiones. Por supuesto, se puede añadir aleatoriedad en escalas más pequeñas, la situación se mezcla.

Las nociones de los movimientos "buenos" y "malos" del gráfico inicial cambian mucho aquí.

Por supuesto, las propiedades de un gráfico cambian. Por ejemplo, un sistema que vende a un movimiento ascendente por 20 puntos (la velocidad de -1) y compra a un movimiento descendente, generalmente gana aproximadamente lo mismo en un periodo largo que lo que pierde en las extensiones. Esto no pasará con un gráfico así.

Hay problemas relacionados con la inestabilidad que están relacionados con la discreción de la toma de decisiones, la expansión y otros factores de este tipo. Sin embargo, hay algunas maneras limitadas de suavizar y aumentar la persistencia, que mejora la situación en cierta medida.

Generalmente, surgen las siguientes preguntas: ¿Es posible, en principio, controlar satisfactoriamente un proceso así? ¿En un intervalo largo de tiempo, las probabilidades de ganar o perder la misma cantidad de puntos sería 50/50? Puede que sí. Por ejemplo, hay una función así como módulo. Matemáticamente, un gráfico aleatorio está siempre por encima de cero. Probablemente no funcionaría como se quiere, pero esto está determinado sólo por el gráfico. Es decir, los problemas aquí no están estrictamente relacionados con la aleatoriedad. Sin embargo, estos produce una gran variedad de limitaciones que merecen la pena, en mi opinión.

Ventajas. Lo primero, la abstracción. No te perjudica ninguna crisis, no te importa si el gráfico inicial se mueve ni cómo lo hace. Por supuesto, puede haber una crisis sin causas visibles, hay que tenerlo en cuenta. En este caso, es más fácil considerarlo utilizando unos principios de trabajo un poco diferentes.

Segundo, puede hacer tantos gráficos como quiera. Como en el ejemplo de arriba: Deje que su sistema descienda gradualmente, mientras un movimiento ascendente raro pero fuerte compensa los retrocesos. Luego, con los sistemas de este tipo correctamente sincronizados, se puede obtener el resultado de la suma en una apariencia más estándar. También es posible un trabajo paralelo de sistemas con otras propiedades.

Tercero, los riesgos se reducen mucho. El tradig se puede modelar para hasta 100 años.

El cambio continuo que significa que la expansión es un problema parecido. Necesita la sincronización de un número grande de sistemas. Siempre se puede "congelar" parte de los sistemas si uno o dos periodos para que la velocidad añadida después no es muy diferente de la precedente. Lo principal es no superponer. También puede hacerlo para que la velocidad sea siempre igual a uno o cero. Pero eso no tiene sentido. Las condiciones adicionales como priorizar los sistemas "congelados" y otras técnicas, harán que la velocidad sea menos oscilante, pero no afectará mucho a la capacidad del sistema.

También hay dos inconvenientes importantes. El primero tiene que ver con la inestabilidad y discreción que se describe arriba. El segundo es una de las probabilidades de los movimientos de los gráficos resultantes. Es difícil cambiarlos en el rango de valores apropiados para trabajar con ellos. La situación puede mejorar por algunos métodos que le permiten aumentar considerablemente los beneficios si el sistema es un poco rentable. Sin embargo, estos valores críticos se determinan principalmente por el desarrollo de los métodos.

Algunas palabras sobre la discreción de la toma de decisiones. Por cierto, a veces ayuda. Compruebo a menudo todos los sistemas en un periodo estricto de 1 hora y media. Luego hago las correcciones para ajustarlos a las propiedades de los sistemas y hago los cambios según la situación. Es mejor adjuntar los momentos de posibles cambios de velocidad a alguna discreción, excepto en situaciones extraordinarias. Esto ayudará a reducir las pérdidas en las expansiones, porque si hay muchos sistemas paralelos trabajando simultáneamente, al final se suman sus velocidades, y las pérdidas sumadas resultan ser más pequeñas que la suma de las pérdidas de los sistemas individuales.

Estas técnicas, como TakeProfit y StopLoss, como regla, son mejores para usarlas en los últimos niveles. En las primeras etapas, sería mejor utilizar transformaciones continuas.

Bueno, finalmente, mirando las actividades de cada sistema desde "fuera", es muy difícil tener una perspectiva de su lógica de funcionamiento. Especialmente si hay procesos aleatorios dentro.

Conclusión

Es a menudo una práctica para estimar los logros de la ciencia sólo mediante sus resultados prácticos.
Por lo que resulta que quien escoge la manzana es la persona que ha hecho el trabajo principal,
cuando, de hecho, la manzana la hizo quien plantó el manzano.

P.L Kapitsa

Aquí he mostrad algunos casos extremos (sólo el uso de respuesta, el uso de gráficos pseudo aleatorios, etc.) que han resultado ser bastante viables. Si alguna vez producen tantas oportunidades, habrá muchas más variaciones intermediarias. Esto ofrece mucha flexibilidad, puede haber una gran cantidad de elecciones variadas. Lo que he mostrado aquí es sólo una pequeña parte de lo que se puede hacer de verdad.

No escribí sobre varias características pequeñas que no se pueden hacer en estos casos extremos. Por ejemplo, si los parámetros no se configuran con mucha exactitud o no se prevén medidas especiales, la discretización puede resultar en que el sistema de tipo servo excede su tarea (que no se ha previsto) y se mueve a una distancia más grande. Sin embargo, ese límite puede determinar un retroceso. Aparece especialmente cuando se trabaja con procesos que se desvían.

Entre los desarrollos de las tecnologías de la información, la liquidez aumentada y las expansiones reducidas y comisiones, estos métodos pueden ganar importancia.

Por supuesto no es muy fácil trabajar con estas cosas, pero las perspectivas no son malas. Todo esto parece imposible a menudo. Esta duda resulta en cambios de los puntos de vista, encontrar nuevas oportunidades, principios, técnicas. Afortunadamente, somos todo apariencias. No puedo decir que haya hecho grandes avances. 1 año y medio no es un periodo muy largo para estas cosas (tan complicadas como parecen). La mayoría del tiempo era sólo una afición para mí. Sin embargo, esta afición ahora tiende a convertirse en mi actividad profesional tras los primeros resultados positivos obtenidos. Por cierto, me encantaría trabajar en esto con un equipo. Pero eso es otro tema. Trabajemos, creemos y seamos mejores siempre.

Saludos.