Neural networks made easy (Part 47): Continuous action space
2 712
1
Introduction
In our previous article, we trained the agent only to determine the trading direction. The Agent's range of actions was limited to only 4 options:
- buy,
- sell,
- hold/wait,
- close all positions.
Here we do not see capital and risk management functions. We used the minimum lot in all trading operations. This is enough to evaluate training approaches, but not enough to build a trading strategy. A profitable trading strategy simply must have a money management algorithm.
In addition, to create a stable trading strategy, we need to manage risks. This block is also missing from our designs. The EA assessed the market situation at each new trading candle and made a decision on a trading operation. But every upcoming bar carries risks for our account. Price movement within a bar can be detrimental to our balance. This is why it is always recommended to use stop losses. This simple approach allows us to limit risks per trade.
1. Continuous action space training features
It is logical that when training the Agent and building its trading policy, we need to take these features into account. But here the question arises: how to train the model to predict the volume of the transaction and the closing levels of the position. This can be easily achieved using supervised learning algorithms where we can specify the required target values provided by the teacher. But there are some complications when using reinforcement learning algorithms.
As you might remember, we previously used 2 approaches to training reinforcement models: reward prediction and the probability of receiving the maximum reward.
One possible way to solve this problem is to define discrete values for all parameters of a trade operation and create a separate action for each of the possible options. This will allow us to take into account some aspects of capital and risk management.
But this approach is not without its drawbacks. Selecting discrete transaction parameters requires some work at the data preparation stage. Their choice will always be a compromise between the number of options and sufficient flexibility in the Agent's decision-making. In this case, the number of combinations of possible actions can increase significantly, which will lead to a more complex model and increase its training time. After all, during the training, you will need to study the reward for each of the possible actions.
For example, if we take only 3 discrete values for trade volume, 3 stop loss levels and 5 take profit levels, then we will need 90 elements just to define the action space in 2 trading directions (3 * 3 * 5 * 2 = 90). Also, do not forget about the actions of holding and closing a position. There are already 92 options in the range of possible agent actions.
Agree, such meager freedom of Agent's action leads to a significant increase in the number of neurons at the output of the model. Addition of each discrete value of any of the trade parameters leads to an increase in the number of neurons in progression.
In addition, training a more complex model may require additional examples of the training set with all the ensuing consequences.
But there are other approaches, so-called algorithms for training an agent in a continuous action space. An agent trained by such algorithms can select actions from a continuous range of values. This allows it to more flexibly and accurately manage transaction parameters, including trading volume, stop loss and take profit levels.
One of the most popular algorithms for training an agent in a continuous action space is Deep Deterministic Policy Gradient (DDPG). In DDPG, the model consists of two neural networks: Actor and Critic. The Actor predicts the optimal action based on the current state, and the Critic evaluates this action. We have already seen a similar solution in the article "Advantage Actor-Critic algorithm". In these algorithms, there are similarities in approaches, but the difference is in the Actor training algorithm.
In DDPG, an Actor is trained using gradient lifting to optimize a deterministic policy. The Actor directly predicts the optimal action based on the current state, rather than modeling the probability distribution of actions as in the advantage actor-critic algorithm.
Actor training in DDPG occurs by calculating the gradient of the Critic value function with respect to the Actor's actions and using this gradient to update the Actor's parameters. It sounds a little complicated, but it allows the Actor to find the optimal action that maximizes the critic's score.
It is important to note that DDPG refers to off-policy algorithms. The model is trained on data obtained from previous interactions with the environment, regardless of the current decision-making strategy. This important property of the algorithm allows it to be used in complex and stochastic environments, where predicting the dynamics of the environment may be difficult or inaccurate. We encountered poor quality of financial market forecasting when testing the EDL algorithm.
The Deep Deterministic Policy Gradient algorithm is based on the core principles of the Deep Q-Network (DQN) and incorporates many of its approaches, including experience replay buffer and target model. Let's take a closer look at the algorithm.
As mentioned above, the model consists of 2 neural networks: Actor and Critic. The Actor receives the state of the environment as input. At the output of the Actor, we obtain the action from a continuous distribution of values. In our case, we will form the transaction volume, stop loss and take profit levels. Depending on the model architecture and problem statement, we can use absolute or relative values. To increase the level of exploration of the environment, some noise can be added to the generated action.
We perform the action chosen by the actor and move to a new state of the environment. In response to the action we take, we receive a reward from the environment.
We collect the "State - Action - New State - Reward" data sets into the experience playback buffer. This is a typical course of actions in case of reinforcement learning algorithms.
As in DQN, we select a package for training the model from the experience playback buffer. The states from this training data package are fed to the Actor's input. Before changing the parameters, we will most likely get an action similar to that stored in the experience playback buffer. But unlike the advantage Actor-Critic, Actor returns not a probability distribution, but an action from a continuous distribution.
To evaluate the value of a given action, we transmit the current state and the generated action to the Critic. Based on the data received, the critic predicts the reward, just like in the conventional DQN.
Similar to DQN, the Critic is trained to minimize the standard deviation between the predicted reward and the actual one from the experience replay buffer. To build a holistic policy, the Target Net model is used. But since the evaluation of the subsequent state requires setting data from the state and the action, then we will also use the target model of the Actor to form an action from the subsequent state.
The highlight of DDPG is that we will not use target output values to train the Actor. Instead, we simply take the error gradient value of the Critic model over our action and pass it further through the Actor model.
Thus, while training the Critic’s Q-function, we use the error gradient over the action to optimize the Agent’s actions. We can say that the Actor is an integral part of the Q-function. Training the Q-function leads to optimization of the Actor function.
But here we should pay attention that in the process of training the Critic, we optimize its parameters for the most correct assessment of the state-action pair. While training the Actor, we optimize its parameters to increase the predicted reward, all other things being equal.
The authors of the method recommend using soft updating of target models. A simple replacement of the target model with a trained one at a certain frequency is replaced by recalculation of the parameters of the target model, taking into account the update rate towards the parameters of the trained model. According to the authors, this approach slows down the updating of target models, but increases the stability of training.
2. Implementation using MQL5
After a theoretical introduction to the Deep Deterministic Policy Gradient (DDPG) method, let's move on to its practical implementation using MQL5. We will start by arranging the soft update of target models. The function of weighted summation of 2 parameters itself is not complicated, but there are 2 points.
First, the operation must be performed with all model parameters. Since the operation of each individual parameter is completely independent of other parameters of the same model, they can be easily executed in parallel.
Secondly, all operations for training and operating models are performed in the context of OpenCL. Data copy operations between context memory and main memory are quite expensive. We have always strived to minimize them. It is logical that parameters should also be recalculated in the context of OpenCL.
2.1. Soft update of target models
First, we will create the SoftUpdate kernel to perform the operations. The kernel algorithm is quite simple. In the kernel parameters, we pass pointers to 2 data buffers (parameters of the target and trained models) and the update factor as a constant.
__kernel void SoftUpdate(__global float *target, __global const float *source, const float tau ) { const int i = get_global_id(0); target[i] = target[i] * tau + (1.0f - tau) * source[i]; }
We will update only one parameter in each separate thread. Therefore, the number of threads will be equal to the number of parameters being updated.
Next, we have to arrange the process on the side of the main program.
Let me remind you that our model parameters are distributed across different objects depending on the type of neural layer. This means we need to add a method for updating parameters to each class for arranging the work of the neural layer. Let's look at the example of the base class of the CNeuronBaseOCL neural layer.
Since we will update the parameters of the current neural layer, we just need to pass a pointer to the neural layer of the trained model and the update coefficient in the method parameters.
bool CNeuronBaseOCL::WeightsUpdate(CNeuronBaseOCL *source, float tau) { if(!OpenCL || !Weights || !source || !source.Weights) return false;
In the body of the method, we check the validity of the received pointer to the neural layer object. Together with it, we will check the pointers to the necessary internal objects.
Here we check the correspondence between the types of the two neural layers and the dimensions of the parameter matrices.
if(Type() != source.Type()) return false; if(Weights.Total() != source.Weights.Total()) return false;
After successfully passing the control block, we organize the transfer of parameters to the kernel.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {Weights.Total()}; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_target, Weights.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_source, source.getWeightsIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SoftUpdate, def_k_su_tau, (float)tau)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Put the kernel into the execution queue. Do not forget to control the process at every step.
if(!OpenCL.Execute(def_k_SoftUpdate, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Complete the method execution.
Since all objects of arranging the work of neural layers of various architectures in our class are inherited from the CNeuronBaseOCL base class, then all classes will inherit the created method. But it only allows us to update the weight matrix of the base class. We should override the method in all classes that add auxiliary internal optimizable objects. For example, in the CNeuronConvOCL convolutional layer, we added a matrix of convolution parameters. To update it, we will override the WeightsUpdate method. To support overriding of inherited methods, we keep all method parameters unchanged.
bool CNeuronConvOCL::WeightsUpdate(CNeuronBaseOCL *source, float tau) { if(!CNeuronBaseOCL::WeightsUpdate(source, tau)) return false;
We do not repeat the entire block of controls in the body of the method. Instead, we call the parent class method and check the result of the operations.
Next, in the parameters, we receive the pointer to the object of the base class of the neural network. This is done intentionally. Specifying the type of the parent class allows you to pass a pointer to any of its descendants. This is what we need to arrange a virtual method in all inherited classes.
But the question is that in this state we cannot access the convolution weight matrix of the layer obtained in the parameters. There is simply no such object in the parent class. It only appears in the convolutional layer class. We have no doubt that the pointer to the convolutional layer is passed in the parameters. In the parent class method, we checked the correspondence of the types of the current neural layer and the one obtained in the parameters. To work with this convolutional layer object, we just need to assign the resulting pointer to the dynamic convolutional layer object. Then we check the compliance of the matrix sizes.
CNeuronConvOCL *temp = source; if(WeightsConv.Total() != temp.WeightsConv.Total()) return false;
Next, we repeat the procedure of transferring data and placing the kernel in the execution queue. Note that only the applied data buffer objects are changed.
uint global_work_offset[1] = {0}; uint global_work_size[1] = {WeightsConv.Total()}; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_target, WeightsConv.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_SoftUpdate, def_k_su_source, temp.WeightsConv.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_SoftUpdate, def_k_su_tau, (float)tau)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_SoftUpdate, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
In a similar way, we create methods in all other classes of neural layers, in which we added objects with optimized parameters. I will not give the complete code of the class methods. You can find them in the attachment.
The operating algorithm of our library does not provide for direct user access to the neural layers of the model. The user always works with the top-level class of the neural network model. Therefore, after adding methods to the neural layer classes, we will create a method of the same name in our CNet::WeightsUpdate model class. In the parameters, the method receives a pointer to the trained neural network and the update coefficient. In the body of the method, we arrange the cycle of searching through all the neural networks of the model and calling methods for updating the neural layer. The algorithm is quite simple. There is no point in providing its code in the article. You can find it in the attachment.
2.2. Data exchange between Actor and Critic
After arranging the update of the models, we proceed directly to arranging the process of training the model. Our model is a kind of symbiosis of the DDPG algorithm with previously studied approaches. In particular, I decided to use a single block of preliminary processing of the source data for both neural networks (Actor and Critic).
The Actor makes a decision on the optimal action based on the obtained state of the environment. The Critic receives as input a description of the state of the environment and the action of the Actor. Based on the data received, it makes a forecast of the expected reward (evaluates the Actor’s action). As we can see, the Actor and Critic receive a description of the environment. In order to minimize repeated operations, it was decided to organize a block of preliminary handling of source data in the Actor body. The Critic should convey a compressed representation of the state of the environment from the latent state of the Actor. In order to minimize the amount of data transfer between the Actor and the Critic on the side of the main program, it was decided to create additional forward and backward pass methods with the transfer in pointers not of individual data buffers, but directly of pointers to the source data model and the identifier of the layer with the source data.
The arranging of the CNet::feedForward forward pass method will be considered. The method parameters provide for the transfer of 2 pointers to neural networks (main and additional source data) and 2 identifiers of neural layers in these networks.
bool CNet::feedForward(CNet *inputNet, int inputLayer=-1, CNet *secondNet = NULL, int secondLayer = -1) { if(!inputNet || !opencl) return false;
Default values have been added to the parameters, which allows us to use the method by passing only one pointer to the main source data model.
In the method body, we check the received pointer to the main source data model. If there is no data, exit the method with a negative result.
Next, we check the ID of the neural layer in the main input data model. If for some reason it was not specified, then we will use the last neural layer of the model.
if(inputLayer<0) inputLayer=inputNet.layers.Total()-1;
At the next stage, we arrange work to access additional data. We create a null pointer to the data buffer object. Check the relevance of the pointer to the model of additional source data.
CBufferFloat *second = NULL; bool del_second = false; if(!!secondNet) { if(secondLayer < 0) secondLayer = secondNet.layers.Total() - 1; if(secondNet.GetOpenCL() != opencl) { secondNet.GetLayerOutput(secondLayer, second); if(!!second) { if(!second.BufferCreate(opencl)) { delete second; return false; } del_second = true; } } else { if(secondNet.layers.Total() <= secondLayer) return false; CLayer *layer = secondNet.layers.At(secondLayer); CNeuronBaseOCL *neuron = layer.At(0); second = neuron.getOutput(); } }
If we have a valid pointer to the model of additional source data, we have 2 options for the development of events:
- If the additional source data model and the current model are loaded in different OpenCL contexts, then we will have to reload the data in any case. We copy the data from the corresponding data model layer into a new buffer and create a buffer in the required context.
- Both models are in the same OpenCL context. The data already exists in the context memory. We just need to copy the pointer to the results buffer of the desired neural layer.
After receiving the buffer with additional source data, we move on to the model of the main source data. As above, we check whether the models are loaded into memory of the same OpenCL context. If not, then we simply copy the original data to the buffer and call the previously developed forward pass method.
if(inputNet.opencl != opencl) { CBufferFloat *inputs; if(!inputNet.GetLayerOutput(inputLayer, inputs)) { if(del_second) delete second; return false; } bool result = feedForward(inputs, 1, false, second); if(del_second) delete second; return result; }
If both models are in the same OpenCL context, then we replace the source data layer with the specified neural layer from the source data model.
CLayer *layer = inputNet.layers.At(inputLayer); if(!layer) { if(del_second) delete second; return false; } CNeuronBaseOCL *neuron = layer.At(0); layer = layers.At(0); if(!layer) { if(del_second) delete second; return false; } if(layer.At(0) != neuron) if(!layer.Update(0, neuron)) { if(del_second) delete second; return false; }
After that, we arrange the cycle of enumerating all neural layers, followed by calling forward pass methods.
for(int l = 1; l < layers.Total(); l++) { layer = layers.At(l); neuron = layer.At(0); layer = layers.At(l - 1); if(!neuron.FeedForward(layer.At(0), second)) { if(del_second) delete second; return false; } } //--- if(del_second) delete second; return true; }
Upon completion of the loop iterations, exit the method with a positive result.
Let's create the CNet::backProp method in a similar way. Its full code is available in the attachment.
We will use both of these methods when training the Critic. But to train the Actor, we need another reverse pass method. The fact is that in the backward pass method, before passing the error gradient through the neural layers, we first determined the deviation of the forward pass results from the target values. The DDPG method eliminates this process for the Actor. For the practical implementation of this algorithm, the CNet::backPropGradient method was created.
In the method parameters, we pass pointers to 2 data buffers: additional source data and the error gradient to them. Both buffers have default values, which allows us to run the method without specifying parameters.
bool CNet::backPropGradient(CBufferFloat *SecondInput = NULL, CBufferFloat *SecondGradient = NULL) { if( ! layers || ! opencl) return false; CLayer *currentLayer = layers.At(layers.Total() - 1); CNeuronBaseOCL *neuron = NULL; if(CheckPointer(currentLayer) == POINTER_INVALID) return false;
In the body of the method, we first check the relevance of pointers to objects of the dynamic array of neural layers and the OpenCL context. Let's declare the necessary local variables.
Then we arrange the loop for distributing the error gradient across all neural layers of the model.
//--- Calc Hidden Gradients int total = layers.Total(); for(int layerNum = total - 2; layerNum >= 0; layerNum--) { CLayer *nextLayer = currentLayer; currentLayer = layers.At(layerNum); if(CheckPointer(currentLayer) == POINTER_INVALID) return false; neuron = currentLayer.At(0); if(!neuron || !neuron.calcHiddenGradients(nextLayer.At(0), SecondInput, SecondGradient)) return false; }
Please note that when arranging the process, we assume that the error gradient is already in the buffer of the last neural layer. This is provided by the DDPG algorithm (Critic error gradient based on Agent actions). There is no control for the presence of an error gradient. The application of the method is the user's responsibility.
After distributing the error gradient, we will update the weighting coefficient matrices.
CLayer *prevLayer = layers.At(total - 1); for(int layerNum = total - 1; layerNum > 0; layerNum--) { currentLayer = prevLayer; prevLayer = layers.At(layerNum - 1); neuron = currentLayer.At(0); if(!neuron.UpdateInputWeights(prevLayer.At(0), SecondInput)) return false; }
Here we should remember that in the neural layer methods we only put kernels in the execution queue. But before performing a subsequent forward pass, we need to be sure that the reverse pass operation is complete. To gain this confidence, we will load the results of the last kernel update of the weight matrix.
bool result=false; for(int layerNum = 0; layerNum < total; layerNum++) { currentLayer = layers.At(layerNum); CNeuronBaseOCL *temp = currentLayer.At(0); if(!temp) continue; if(!temp.TrainMode() || !temp.getWeights()) continue; if(!temp.getWeights().BufferRead()) continue; result=true; break; } //--- return result; }
This concludes our work on updating the methods and classes of our library. Their full code can be found in the attachment.
2.3. Creating a model training EA
Next, we will move on to creating and training the model using the DDPG algorithm. Training is implemented in the "DDPG\Study.mq5" EA.
As we have already mentioned, the created model will combine elements of DDPG and previously discussed approaches. This will be reflected in the architecture of our model. Let's create the CreateDescriptions function to describe the architecture.
In the parameters, the function receives pointers to 2 dynamic arrays for recording objects describing the architecture of the Actor and Critic neural layers. In the body of the function, we check the relevance of the received pointers and, if necessary, create new array objects.
bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
We start with the description of the Actor's architecture. Here we use the GCRL developments and build a model with 2 streams of source data. The Actor's decision-making will be based on the current state of the environment (historical data). We will create a source data layer of the appropriate size for it.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.window = 0; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
The raw data is processed by a batch normalization layer and passed through a block of convolutional layers.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count - 1; descr.window = 2; descr.step = 1; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = 8; descr.step = 8; descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Next, we compress the data in 2 fully connected layers. All this may remind you of the previously used Encoder.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.optimization = ADAM; descr.activation = LReLU; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 128; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
An assessment of the market situation may be sufficient to determine the direction of trading and stop loss/take profit levels. However, it is not enough for money management functions. At this stage, we will add information about the state of the account just like when stating the model problem.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 256; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = LReLU; if(!actor.Add(descr)) { delete descr; return false; }
Remember the ID of this layer and the size of the vector of its results. It is from this layer that we will take the latent representation of the state of the environment as the Critic’s initial data.
Next comes the decision-making block from fully connected layers.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
At the output of the actor, we will have a fully connected layer of 6 elements that represent the transaction volume, its stop loss and take profit (3 elements for buying and 3 for selling).
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 6; descr.optimization = ADAM; descr.activation = LReLU; if(!actor.Add(descr)) { delete descr; return false; }
In a simplified form, we do not add elements for the actions of closing positions and waiting for a suitable entry/exit point. We assume that positions will be closed using stop loss or take profit. The issuance of incorrect values for one of the transaction indicators corresponds to the absence of a trading operation.
The Critic model uses the current state of the environment and the Actor's action to predict rewards. In our case, both flows of information come from the Actor model, although from different neural layers, and, accordingly, from different data buffers. We will use neural data concatenation layer to combine two data streams. This will be reflected in the architecture of the Critic model as follows. We will transfer the first data stream (latent representation of the current state) to the source data layer. The size of this layer should correspond to the size of the Actor neural layer, we plan to take data from.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = 256; descr.window = 0; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
The data comes from the internal state of another model and we can skip the data normalization layer.
Next, we use a concatenation layer to combine 2 streams of information. The size of the additional data is equal to the size of the Actor results layer.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 128; descr.window = prev_count; descr.step = 6; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; }
Then comes the decision block consisting of 2 fully connected layers.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 128; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 128; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; }
The fully connected layer with 1 element without the activation function is used at the Critic output. Here we expect to get the predicted reward.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 1; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
In order not to be confused in the future with the identifier of the layer of the latent representation of the environment state, we will define a constant in the form of a macro substitution.
#define LatentLayer 6
Now that we have decided on the architecture of the models, we are moving on to working on the EA algorithm. First, we will create the OnInit method for initializing the EA. At the beginning of the method, as before, we initialize the objects of indicators and trading operations.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if(!Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh(); //--- if(!RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice)) return INIT_FAILED; //--- if(!CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice)) return INIT_FAILED; //--- if(!ATR.Create(Symb.Name(), TimeFrame, ATRPeriod)) return INIT_FAILED; //--- if(!MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice)) return INIT_FAILED; if(!RSI.BufferResize(HistoryBars) || !CCI.BufferResize(HistoryBars) || !ATR.BufferResize(HistoryBars) || !MACD.BufferResize(HistoryBars)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); return INIT_FAILED; } //--- if(!Trade.SetTypeFillingBySymbol(Symb.Name())) return INIT_FAILED;
Then we attempt to load the pre-trained models. If they do not exist, then we start creating models.
Here we should pay attention to one nuance. While we previously created a training model and copied it completely into the target model, now we initialize the training and target models with random parameters. Moreover, both models use the same architecture.
//--- load models float temp; if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !Critic.Load(FileName + "Crt.nnw", temp, temp, temp, dtStudied, true) || !TargetActor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic.Load(FileName + "Crt.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Actor.Create(actor) || !Critic.Create(critic) || !TargetActor.Create(actor) || !TargetCritic.Create(critic)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; //--- }
Next, we will transfer all models to a single OpenCL context. This will allow us to operate with pointers to data buffers without physical copying when transferring information between models.
COpenCLMy *opencl = Actor.GetOpenCL(); Critic.SetOpenCL(opencl); TargetActor.SetOpenCL(opencl); TargetCritic.SetOpenCL(opencl);
This is followed by a block for monitoring the conformity of model architectures.
Actor.getResults(Result); if(Result.Total() != 6) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", 6, Result.Total()); return INIT_FAILED; } ActorResult = vector<float>::Zeros(6); //--- Actor.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Actor.GetLayerOutput(LatentLayer, Result); int latent_state = Result.Total(); Critic.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Initialize global variables and terminate the method.
PrevBalance = AccountInfoDouble(ACCOUNT_BALANCE); PrevEquity = AccountInfoDouble(ACCOUNT_EQUITY); FirstBar = true; Gradient.BufferInit(AccountDescr, 0); Gradient.BufferCreate(opencl); //--- return(INIT_SUCCEEDED); }
We determined that the target models would be updated after each episode. Therefore, this functionality was included in the EA deinitialization method. We first update the target models. Then we save them. Note that we save the target models, not the trained ones. Thus, we want to minimize the retraining of the model for a single episode.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- TargetActor.WeightsUpdate(GetPointer(Actor), Tau); TargetCritic.WeightsUpdate(GetPointer(Critic), Tau); TargetActor.Save(FileName + "Act.nnw", Actor.getRecentAverageError(), 0, 0, TimeCurrent(), true); TargetCritic.Save(FileName + "Crt.nnw", Critic.getRecentAverageError(), 0, 0, TimeCurrent(), true); delete Result; }
The actual process of training the model is carried out in the action flow. In our case, we will train the model in the strategy tester in the history walkthrough mode. We will not create the experience replay buffer. Its role will be performed by the strategy tester itself. Thus, the entire learning process is arranged in the OnTick function.
At the beginning of the function, we check for the new candle open event. After that, we update the data of indicators and historical data on the movement of the instrument’s price in the buffers.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- if(!IsNewBar()) return; //--- int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates); if(!ArraySetAsSeries(Rates, true)) return; //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); Symb.Refresh(); Symb.RefreshRates();
The data preparation process has been completely transferred from the previously discussed EAs. There is now point in describing it here. Find the full EA code and all its functions in the attachment.
After preparing the initial data, we check whether a forward pass of the trained model has previously been carried out. If there is a forward pass, carry out a reverse passage. To assess the current state, we will perform a forward pass of the target model. Note that we first perform a forward pass of the target Actor model. We carry out a direct pass of the Critic’s target model considering the formed action. Add the actual reward of the system in the form of a change in the account balance to the resulting value. Also, if there are no open positions, we will add a penalty in order to encourage the Actor to actively trade and call the reverse pass first of the Critic and then of the Actor.
if(!FirstBar) { if(!TargetActor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) return; if(!TargetCritic.feedForward(GetPointer(TargetActor), LatentLayer, GetPointer(TargetActor))) return; TargetCritic.getResults(Result); float reward = (float)(account[0] - PrevBalance + Result[0]); if(account[0] == PrevBalance) if((buy_value + sell_value) == 0) reward -= 1; Result.Update(0, reward); if(!Critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(PrevAccount), GetPointer(Gradient))) return; }
Note that for the Critic reverse pass we use the updated backProp method passing the buffer of target values and the pointer to the Actor model. At the same time, we do not indicate the identifier of the latent layer, since we replaced objects previously (during the direct pass).
For the backward pass of the Actor, we use the backPropGradient method in which the gradient from the Critic reverse pass propagates through the model.
Performing a reverse pass of the Critic and the Actor allows us to optimize the Q function of our model.
Next, we will perform the forward pass through the trained model.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) return; if(!Critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) return;
Here it is worth paying attention to the following aspect: in the process of training the Q-function, we only improve the quality of the prediction of the expected reward. However, we do not train the Actor to increase the profitability of its actions. For this purpose, the DDPG algorithm provides for updating the Actor’s parameters in the direction of increasing the predicted reward. It is worth noting that at this point we are passing the error gradient through the Critic, but not updating its parameters. Therefore, we disable updating the Critic weight matrices by setting the TrainMode flag to 'false'. After the Actor's reverse pass, we return the flag position to 'true'.
if(!FirstBar) { Critic.getResults(Result); Result.Update(0, Result.At(0) + MathAbs(Result.At(0) * 0.0001f)); Critic.TrainMode(false); if(!Critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) return; Critic.TrainMode(true); }
Save the value for operations on the next bar into global variables.
FirstBar = false; PrevAccount.AssignArray(GetPointer(Account)); PrevAccount.BufferCreate(Actor.GetOpenCL()); PrevBalance = account[0]; PrevEquity = account[1];
Then we just have to decipher the results of the actor’s work and carry out trading operations. In this example, we train the Actor to provide absolute values of trade volume and trading levels. We only normalize the data and convert the levels into specific price values.
vector<float> temp; Actor.getResults(temp); float delta = MathAbs(ActorResult - temp).Sum(); ActorResult = temp; //--- double min_lot = Symb.LotsMin(); double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point(); double buy_lot = MathRound((double)ActorResult[0] / min_lot) * min_lot; double sell_lot = MathRound((double)ActorResult[3] / min_lot) * min_lot; double buy_tp = NormalizeDouble(Symb.Ask() + ActorResult[1], Symb.Digits()); double buy_sl = NormalizeDouble(Symb.Ask() - ActorResult[2], Symb.Digits()); double sell_tp = NormalizeDouble(Symb.Bid() - ActorResult[4], Symb.Digits()); double sell_sl = NormalizeDouble(Symb.Bid() + ActorResult[5], Symb.Digits()); //--- if(ActorResult[0] > min_lot && ActorResult[1] > stops && ActorResult[2] > stops && buy_sl > 0) Trade.Buy(buy_lot, Symb.Name(), Symb.Ask(), buy_sl, buy_tp); if(ActorResult[3] > min_lot && ActorResult[4] > stops && ActorResult[5] > stops && sell_tp > 0) Trade.Sell(sell_lot, Symb.Name(), Symb.Bid(), sell_sl, sell_tp);
Let me remind you that we did not provide for a separate action of the Actor to wait for a suitable situation. Instead, we use invalid trade parameter values. Therefore, we check the correctness of the received parameters before sending a trade request.
It is worth noting one more point that is not provided for by the considered algorithm, but was added by me. It does not contradict the considered method. It only introduces some restrictions into the Actor’s training policy. This way I wanted to introduce some framework into the volume of the opened position and the size of trading levels.
When receiving incorrect or inflated transaction parameters, I formed a vector of random target values within the specified limits and carried out a reverse pass of the Actor similar to supervised learning methods. In my opinion, this should return the results of the Actor’s work to the specified limits.
if(temp.Min() < 0 || MathMax(temp[0], temp[3]) > 1.0f || MathMax(temp[1], temp[4]) > (Symb.Point() * 5000) || MathMax(temp[2], temp[5]) > (Symb.Point() * 2000)) { temp[0] = (float)(Symb.LotsMin() * (1 + MathRand() / 32767.0 * 5)); temp[3] = (float)(Symb.LotsMin() * (1 + MathRand() / 32767.0 * 5)); temp[1] = (float)(Symb.Point() * (MathRand() / 32767.0 * 500.0 + Symb.StopsLevel())); temp[4] = (float)(Symb.Point() * (MathRand() / 32767.0 * 500.0 + Symb.StopsLevel())); temp[2] = (float)(Symb.Point() * (MathRand() / 32767.0 * 200.0 + Symb.StopsLevel())); temp[5] = (float)(Symb.Point() * (MathRand() / 32767.0 * 200.0 + Symb.StopsLevel())); Result.AssignArray(temp); Actor.backProp(Result, GetPointer(PrevAccount), GetPointer(Gradient)); } }
Of course, we could use a constraining activation function (such as a sigmoid) as an alternative. But then we would strictly limit the range of possible values. Besides, during the training, we could quickly reach limit values slowing down further training of the model.
After completing all operations, we go into waiting mode for the next tick.
The full code of the EA and all programs used in the article is available in the attachment.
3. Test
After completing work on the model training EA, we move on to the stage of checking the results of the work done. As before, the model is trained on historical data of the EURUSD H1 from the beginning of 2023. All indicator and model training parameters used default values.
Training the model in real time makes its own adjustments and prevents from using several parallel agents. Therefore, the first checks of the correct operation of the EA algorithm were carried out in single run mode. Then the slow optimization mode was selected and only 1 local optimization agent was activated.
In order to regulate the number of training iterations, an external parameter Agent was added, which is not used in the EA algorithm.
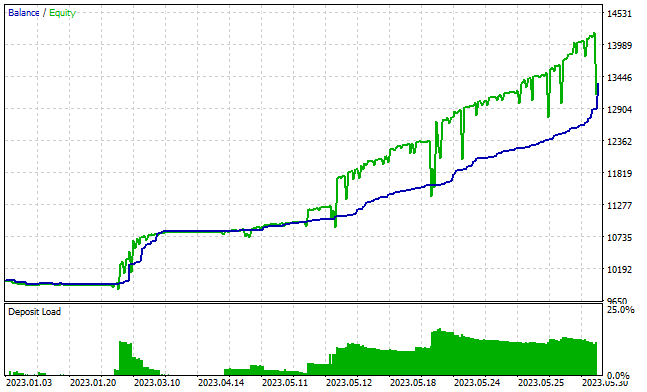
After about 3000 passes, I was able to get a model that was able to generate profit on the training set. During the training period of 5 months, the model made 334 transactions. More than 84% of them were profitable. The result was the profit of 33% of the initial capital. At the same time, the drawdown on balances was less than 1%, and by Equity - 7.6%. The profit factor exceeded 26 and the recovery factor amounted to 3.16. The graph below shows an upward trend in the balance. The balance line is almost always below the Equity line, which indicates that positions are being opened in the right direction. At the same time, the load on the deposit is about 20%. This is a fairly high figure, but does not exceed the accumulated profit.
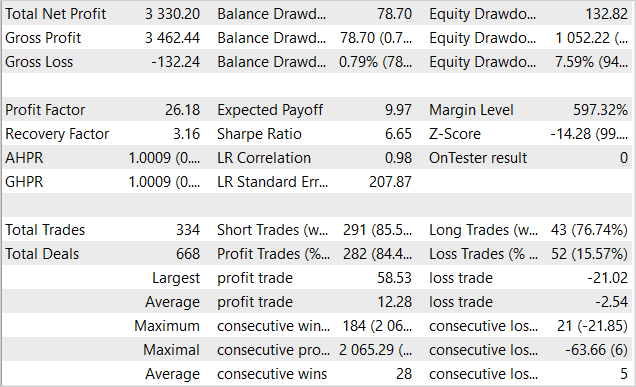
Unfortunately, the results of the EA's work turned out to be more modest outside the training set.
Conclusion
In this article, we explored the application of reinforcement learning in the context of a continuous action space and introduced the Deep Deterministic Policy Gradient (DDPG) method. This approach opens up new opportunities for training the agent to manage capital and risk, which is an important aspect of successful trading.
We have developed and tested the EA for training the model. It not only predicts the direction of a trade, but also determines the transaction volume, stop loss and take profit levels. This allows the Agent to manage investments more efficiently.
During the test, we managed to train the model to generate profit on the training set. Unfortunately, the training provided was not enough to obtain similar results outside the training set. The bottleneck of our implementation is the online training of the model, which does not allow the parallel use of several agents to increase the level of environmental research and reduce the model training time.
The results obtained allow us to hope that it will be possible to train the model for stable operation outside the training set.
List of references
Programs used in the article
| # | Name | Type | Description |
|---|---|---|---|
| 1 | Study.mq5 | Expert Advisor | Agent training EA |
| 2 | Test.mq5 | Expert Advisor | Model testing EA |
| 3 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 4 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/12853
Neural networks made easy (Part 48): Methods for reducing overestimation of Q-function values
Developing an MQTT client for Metatrader 5: a TDD approach — Part 4
Neural networks made easy (Part 49): Soft Actor-Critic
MQL5 Wizard Techniques you should know (Part 07): Dendrograms
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Dmitriy Gizlyk Many thanks for the detailed article. I retrained the model between 1st Jan 2023 and 31st May 2023 to produced DDPGAct.nnw and DDPGCrt.nnw. However, when testing the EA with test.ex5, there wan't a single trade.
I have taken the following steps:
Trying to debug with the following PrintFormat lines:
reviewed the following:
... 2023.12.01 23:15:18.641 Core 01 2023.05.30 19:00:00 ActorResult[0]=0.085580 ActorResult[1]=-0.000476 ActorResult[2]=-0.000742 buy_sl=1.072910 2023.12.01 23:15:18.641 Core 01 2023.05.30 19:00:00 ActorResult[3]=0.085580 ActorResult[4]=-0.000476 ActorResult[5]=-0.000742 sell_tp=1.070290 2023.12.01 23:15:18.641 Core 01 2023.05.30 20:00:00 ActorResult[0]=0.085580 ActorResult[1]=-0.000476 ActorResult[2]=-0.000742 buy_sl=1.072830 2023.12.01 23:15:18.641 Core 01 2023.05.30 20:00:00 ActorResult[3]=0.085580 ActorResult[4]=-0.000476 ActorResult[5]=-0.000742 sell_tp=1.070210 2023.12.01 23:15:18.641 Core 01 2023.05.30 21:00:00 ActorResult[0]=0.085580 ActorResult[1]=-0.000476 ActorResult[2]=-0.000742 buy_sl=1.072450 2023.12.01 23:15:18.641 Core 01 2023.05.30 21:00:00 ActorResult[3]=0.085580 ActorResult[4]=-0.000476 ActorResult[5]=-0.000742 sell_tp=1.069830 2023.12.01 23:15:18.641 Core 01 2023.05.30 22:00:00 ActorResult[0]=0.085580 ActorResult[1]=-0.000476 ActorResult[2]=-0.000742 buy_sl=1.072710 2023.12.01 23:15:18.641 Core 01 2023.05.30 22:00:00 ActorResult[3]=0.085580 ActorResult[4]=-0.000476 ActorResult[5]=-0.000742 sell_tp=1.070090 2023.12.01 23:15:18.641 Core 01 2023.05.30 23:00:00 ActorResult[0]=0.085580 ActorResult[1]=-0.000476 ActorResult[2]=-0.000742 buy_sl=1.073750 2023.12.01 23:15:18.641 Core 01 2023.05.30 23:00:00 ActorResult[3]=0.085580 ActorResult[4]=-0.000476 ActorResult[5]=-0.000742 sell_tp=1.071130 ...May I know what has gone wrong or missed please?
Many thanks.