Category Theory in MQL5 (Part 1)
Introduction
Category Theory is a branch of Mathematics that was brought to life by Eilenberg and Mac Lane in the 1940s. At a time when Einstein’s theory of relativity was leading to the realisation that there is no single perspective from which to view the world but rather the real power lies in being able to translate between these different perspectives, its ideas were born. It therefore serves as a form of classification that does not dwell on the objects being classified per se but rather focuses on the inter-relation of these objects to come up with very concise definition(s). The significance of this approach is that concepts taken from one area of study or discipline can be intuitive or even applicable in a different field. In its beginnings though, the main use was for the study of linkages between geometry and algebra. Today the uses clearly transcend mathematics and are too broad for these series articles so we will dwell on its possible use for traders using MQL programming language.
In the context of trading and writing expert advisors in MQL5, category theory can be used to analyze and understand the relationships between different trading strategies, instruments, and market conditions. It can help traders to identify common patterns and structures in their trading systems and to develop more general and flexible trading algorithms that can adapt to changing market conditions.
Category theory can also be useful for verifying the correctness and consistency of trading systems and for developing formal models of trading behaviour. By providing a clear and rigorous language for expressing and reasoning about trading concepts, category theory can help traders to write more reliable and maintainable expert advisors, as well as to communicate their ideas and strategies more effectively with other traders and researchers.
Domains and Morphisms
Category domains and morphisms are the foundational concepts in category theory. In category theory, a category is a collection of domains (aka sets) of elements and the morphisms (or arrows aka maps, aka functions) between them. For these articles we will take arrows or functions or maps to be the basic units of a morphism. These morphisms encode the relationships between the elements in each domain within the category, and they can be composed to form more complex morphisms.
Sets are a fundamental concept in mathematics, and they play a key role in category theory. In category theory, we refer to them as domains that are used to define the elements of a specific 'kind'. Typically, if we were studying the category of domains, the ‘elements’ of the category would be domains themselves. These domains, usually but not always, go on to contain other elements which form the basis for morphism. The morphisms in this category would be functions between domains, which are rules that associate each element of one domain with a unique element of another domain. For example, if we had two domains A and B, a morphism from A to B would be a rule that assigns each element of A to a unique element of B. When a morphism runs from A to B, A is referred to as 'the domain' while B is the 'codomain'. All the elements in the domain will have a relation with at least one of the elements in the codomain. No element in the domain remains un-mapped. However some elements in the codomain may be unmapped. This is often denoted as follows.
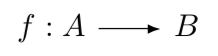
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ class CElement { protected: int cardinal; vector element; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } double Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); } bool Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); } CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
So from the listing above we can start by defining an element. This is the basic unit of a domain which you could take to be a like 'a member of a set'. This unit could take on any data type whether double or integer however the vector type would be more flexible as more complex data types and operations are met. It allows scalability. Its size, the 'cardinal' parameter is protected and can only be accessed or modified through the 'Cardinality()' functions. Protecting its access ensures whenever it is modified, the vector gets appropriately resized. The vector 'element' itself is also protected to prevent invalid index errors. So access is only allowed though the 'Get()' and 'Set()' functions. The 'Set()' function also returns a boolean to check if the assignment was successful.
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ class CDomain { protected: int cardinal; CElement elements[]; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } bool Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); } bool Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); } //only unique elements allowed int New(CElement &Value) { bool _new=-1; // for(int o=0; o<cardinal; o++) { if(ElementMatch(Value,elements[o])) { _new=o; break; } } return(_new); } CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
The domain class therefore is what includes our elements the class of which is covered above. Its main variables 'elements[]' and its size 'cardinal' are protected like in the element class for reasons already mentioned. What is slightly different here is the addition of the 'New()' method. This function helps check new objects that are to be added to the domain, and ensure that they are unique. Category Domains only contain unique objects. No duplicates are allowed.
Since we have these two classes, we could try to construct some domains. Let's try to have a domain of even numbers and one of odd numbers. We could do this by running a script that references these classes. The listing of this is shown as follows.
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); }
The create number function is a straightforward method for populating a domain with natural numbers. All code is attached to this article however it's set is shown here for clarity.
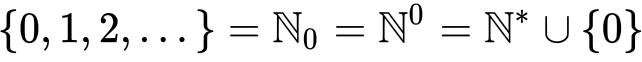
The 'PrintSet()' function is a resourceful method we'll refer to often. It simply allows us to view contents of a domain with appropriate parentheses and commas taking care to separate the element vector structure(s) from the overall domain structure. If we run the above script, this is what we should see.
2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}
The various elements of each domain are in brackets because they are the vector data type meaning they themselves could have multiple entries. When this happens then commas appear between each entry with the brackets then helping define where the element boundaries.
Morphisms are also an important concept in category theory, and they are used to encode the relationships between the elements in domain(s). As per category theory rules each morphism maps one element in the domain to one element in the codomain. These functions can be composed to form more complex morphisms, and they can be used to study the properties of sets and their relationships with other sets as we'll see.
To begin though, there are 5 main types of morphisms, that can be used to describe the relationships between objects in a given category. Some of the most common types are:
- Monomorphisms: These are injective morphisms, which means that they map each element in the source domain to a unique object in the codomain. No two morphisms map to the same object in the codomain. In this instance you may have some objects in the target unmapped.
- Epimorphisms: These are surjective morphisms, which means that the elements in the domain map to all the elements in the codomain. In other words, no element in the codomain is left unmapped. In this instance also, it is common to have fewer elements in the codomain than the source set.
- Isomorphisms: Isomorphisms are bijective morphisms, which means that they establish a one-to-one correspondence between objects in the source and target categories. They are both injective and surjective since the source and target sets have the same number of objects.
- Endomorphisms: Endomorphisms are morphisms from an element to itself. It is what constitutes an identity map, i.e. a group of endomorphisms linking back to the domain.
- Automorphisms: Automorphisms are a map combination of isomorphisms and endomorphisms.
Let us look at how a morphism class and its grouping with domains referred to as a homomorphism can be implemented in MQL.
//+------------------------------------------------------------------+ //| MORPHISM CLASS | //+------------------------------------------------------------------+ class CMorphism { public: int domain; int codomain; CElement morphism; bool Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true) { int _d=D.New(DE),_c=C.New(CE); // if(_d>=0 && _c>=0) { if(DE.Cardinality()==CE.Cardinality()) { domain=_d; codomain=_c; morphism.Cardinality(DE.Cardinality()); if(Add) { for(int c=0;c<morphism.Cardinality();c++) { morphism.Set(c,CE.Get(c)-DE.Get(c)); } } else { for(int c=0;c<morphism.Cardinality();c++) { if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); } } } } } return(false); } CMorphism(void){ domain=-1; codomain=-1; }; ~CMorphism(void){}; };
The morphism class is very basic with just the domain and codomain index parameters plus a 'Morph' function which we will not concern ourselves with for this article. Reference to the respective domain and codomain sets is omitted here because these are listed in the umbrella Homomorphism class as shown below.
//+------------------------------------------------------------------+ //| HOMO-MORPHISM CLASS | //+------------------------------------------------------------------+ class CHomomorphism { protected: int cardinal; CMorphism morphism[]; public: bool init; CDomain domain; CDomain codomain; bool Cardinality(int DomainIndex,int CodomainIndex,bool Add=true) { bool _morphed=true; if ( !init ) { _morphed=false; return(_morphed); } if ( DomainIndex<0 || DomainIndex>=domain.Cardinality() || CodomainIndex<0 || CodomainIndex>=codomain.Cardinality() ) { _morphed=false; return(_morphed); } for(int m=0;m<cardinal;m++) { if(DomainIndex==morphism[m].domain) { _morphed=false; break; } } if(_morphed) { cardinal++; ArrayResize(morphism,cardinal); CElement _de,_ce; if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce)) { morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add); } } return(_morphed); }; int Cardinality() { return(cardinal); }; bool Get(int Index,CMorphism &Morphism) { if(Index>=0 && Index<Cardinality()) { return(true); } return(false); }; bool Set(int Index,CMorphism &Value) { if ( Index>=0 && Index<Cardinality() && Value.domain>=0 && Value.domain<domain.Cardinality() && Value.codomain>=0 && Value.codomain<codomain.Cardinality() ) { if(!MorphismMatch(Index,Value,morphism,Cardinality())) { morphism[Index]=Value; return(true); } } return(false); }; void Init(CDomain &Domain,CDomain &Codomain) { domain=Domain; codomain=Codomain; init=true; } CHomomorphism(void){ init=false; cardinal=0; }; ~CHomomorphism(void){}; };
In the Homomorphism class, the 'morphism[]' variable together with its size 'morphisms' are protected for the afore mentioned reasons above which I will not repeat. Suffice it to say the two 'Morphism()' functions and the 'Get()' and 'Set()' functions follow in similar fashion to the functions in the objects and set classes. What is added here is an 'init' boolean parameter that indicates whether the class has been initialised by assigning the public 'domain' and 'codomain' sets. Adding of a morphism to the protected 'morphism[]' array is by providing a domain index and a codomain index. These indices need to be within the range their respective domain sizes. Once they pass this there is a need to check that the domain index in particular has not been used. As per rules of Category Theory all objects in the domain must map to an object in the codomain but they only map once. So a codomain index can be used twice but a domain index is used only once.
Let's digress a little and look at subdomains (aka. Subsets). Subdomains are a useful tool in Category Theory, and the ability to enumerate subdomains within a domain and check for whether a domain is a possible subdomain to a given domain can be a very resourceful tool. Let's look at functions that accomplish these two tasks.
//+------------------------------------------------------------------+ //| Domain Match function | //+------------------------------------------------------------------+ bool DomainMatch(CDomain &A,CDomain &B) { if(A.Cardinality()!=B.Cardinality()) { return(false); } bool _matched=true; for(int o=0; o<A.Cardinality(); o++) { CElement _a,_b; if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b)) { _matched=false; break; } } return(_matched); } //+------------------------------------------------------------------+ //| Is Subdomain function | //+------------------------------------------------------------------+ bool IsSubdomain(CDomain &Domain,CDomain &SubDomain) { bool _is_subdomain=false; int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(Domain,_subdomain_count,_subdomains); for(int c=0;c<_subdomain_count;c++) { if(DomainMatch(SubDomain,_subdomains[c])) { _is_subdomain=true; break; } } return(_is_subdomain); }
If we therefore run the script below:
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(_evens,_subdomain_count,_subdomains); printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count)); for(int s=0; s<_subdomain_count; s++) { printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1)); } }
It should give us these logs:
2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7 2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7
The actual number of possible subsets is 8 if we include the empty set which is also a subset.
The additional code to check for a subset can be composed as shown:
CDomain _smaller_evens; CreateNumberDomain(_smaller_evens,__domain_elements-2,2); printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens)); bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. "); _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
Its logs should yield this:
2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)} 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds.
In category theory, a homomorphism is a structure-preserving definition of a group of morphisms between two domains. It is a function that preserves the relationships and operations defined on the elements. Homomorphisms are significant in category theory because they provide a means of studying the relationships between different elements, and of constructing new elements from existing ones.
By considering homomorphisms between elements, it is possible to gain insight into the nature of the elements and their behaviour under different operations. For example, the existence of a homomorphism between two domains can be used to define a notion of equivalence between them, allowing for the study of the relationships between them.
Another significance of homomorphisms in category theory is that they provide a means of constructing new objects from existing ones through inheritance these properties. Examples of these together with equivalence will be covered in subsequent articles and are only mentioned here to set the basis for why this seemingly 'non useful' class is being defined.
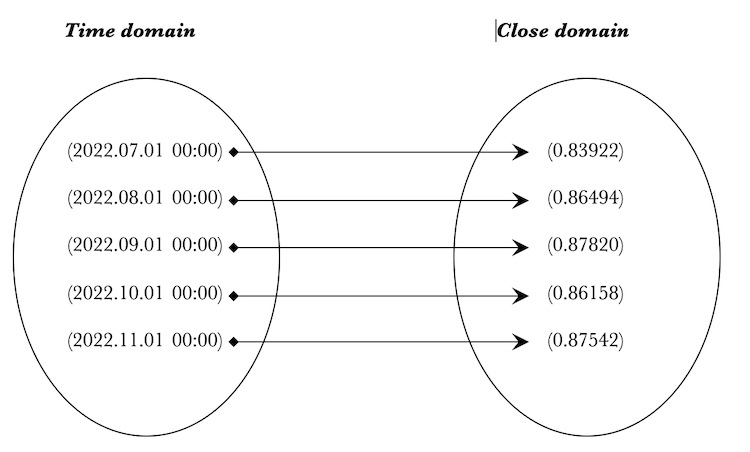
Let's try to enliven Category Theory for our purposes by creating an instance of the homomorphism class that has domain and codomain sets of time and close prices.
We will then view this instance using the 'PrintHomomorphism()' function. These custom print functions are going to be very useful in viewing created objects, sets, morphisms, and homomorphisms. Here is there listing:
//+------------------------------------------------------------------+ //| Print Element function | //+------------------------------------------------------------------+ string PrintElement(CElement &O,int Precision=1,bool IsTime=false) { string _element="("; // for(int r=0; r<O.Cardinality(); r++) { if(!IsTime) { _element+=DoubleToString(O.Get(r),Precision); } else if(IsTime) { _element+=TimeToString(datetime(int(O.Get(r)))); } if(r<O.Cardinality()-1){ _element+=","; } } // return(_element+")"); } //+------------------------------------------------------------------+ //| Print Set function | //+------------------------------------------------------------------+ string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false) { string _set="{"; // CElement _e; for(int o=0; o<S.Cardinality(); o++) { S.Get(o,_e); _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; } } // return(_set+"}\n"); } //+------------------------------------------------------------------+ //| Print Morphism function | //+------------------------------------------------------------------+ string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _morphism=""; // CElement _d,_c; if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c)) { _morphism=PrintElement(_d,Precision,DomainIsTime); _morphism+="|----->"; _morphism+=PrintElement(_c,Precision,CodomainIsTime); _morphism+="\n"; } // return(_morphism); } //+------------------------------------------------------------------+ //| Print Homomorphism function | //+------------------------------------------------------------------+ string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime); // _homomorphism+="|\n"; CMorphism _m; for(int m=0;m<H.Cardinality();m++) { if(H.Get(m,_m)) { _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime)); } } // _homomorphism+="|\n"; _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime); // return(_homomorphism); }
Notable inputs here are 'Precision' and 'IsTime'. These two set decimal places for displaying floating data (the default for vectors) and whether it is necessary to cast the object/ vector data as time for presentation purposes within the returned string.
So to create our homomorphism we will use this script:
//Declare sets to store time & close prices CDomain _time,_close; MqlRates _rates[]; //Fill domain with 5 most recent bar time & MA values from chart if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms)) { for(int m=0;m<__domain_morphisms;m++) { //Create uni row element CElement _t,_m; if(_t.Cardinality(1) && _m.Cardinality(1)) { datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m); _t.Set(0,double(int(_t_value))); _time.Set(m,_t); double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE); _m.Set(0,_m_value); _close.Set(m,_m); } } } //Create homomorphism from time to close CHomomorphism _h;_h.Init(_time,_close); if(_h.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__domain_morphisms;m++) { if(_h.Cardinality(m,m)){ _morphisms++; } } if(_morphisms>=__domain_morphisms) { printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); } }
We create two sets '_time' and "_close'. We then fill them with data from an MqlRates array. '__set_morphisms' is an input parameter that determines the set size. In this case both '"time' and "_close' sets are the same size and they match the input parameter. The homomorphism class instance '_h" is then initialised with these two sets. Simple one-to-one morphisms are created between the two sets using the 'Morphisms()' function which is checked since it returns a boolean. If true the '_morphisms' parameter gets incremented and once we get to the size of the input parameter we print the homomorphism '_h' using Print Homomorphism()' function. Our logs should yield this:
2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)} 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}
In Category Theory it can also be resourceful to enumerate the image set of a homomorphism. An image simply refers to a subset of the codomain that features only the objects mapped to from the domain. For our purposes we can enumerate this using the function below:
//+------------------------------------------------------------------+ //| Image function | //+------------------------------------------------------------------+ void Image(CHomomorphism &H,CSet &Output) { for(int m=0;m<H.Morphisms();m++) { CObject _o; CMorphism _m; if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o)) { bool _matched=false; for(int o=0;o<Output.Objects();o++) { CObject _oo; if(Output.Get(o,_oo) && ObjectMatch(_o,_oo)) { _matched=true; break; } } if(!_matched) { Output.Objects(Output.Objects()+1); Output.Set(Output.Objects()-1,_o); } } } }
To see this code in action we'll use this script:
//Create homomorphism from time to close CHomomorphism _h_image;_h_image.Init(_time,_close); if(_h_image.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__set_morphisms;m++) { int _random_codomain=MathRand()%__set_morphisms; if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; } } if(_morphisms>=__set_morphisms) { CSet _image;_image.Objects(0); Image(_h_image,_image); printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); } }
All we are doing here is using the two previously created sets in a new homomorphism class called '_h_image'. The difference this time is when adding morphisms we randomly choose codomain values and thus have repetition. This means the codomain set will be different from the one in the '_h' instance. Our logs should produce this:
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)
Clearly the codomain just has two objects out of the possible three so from this we can easily retrieve the objects mapped to from a given set. We will continue from here in the next where we will start with isomorphisms and endomorphisms.
Conclusion
We have looked at some introductory concepts of category theory, an increasingly resourceful method in mathematics for classifying information. Among these has been an element, a domain, and a morphism. An element forms the foundational unit and it is typically thought of as a member of a set which in set in category theory is referred to as a domain. This domain through its elements can have relationships with other domains (referred to as codomains). These relationships are termed morphisms. For a trader category theory can serve as a classifier for time series financial information and thus a tool in assessing and forecasting market conditions. We will resume from here in the next article.
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Developing a trading Expert Advisor from scratch (Part 31): Towards the future (IV)
Developing a trading Expert Advisor from scratch (Part 31): Towards the future (IV)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use