Ich sehe keine Verzögerung bei der Bewegung. Das bedeutet, dass der Autor nicht versteht, was er eingestellt hat, oder dass ein Fehler im Algorithmus vorliegt und der Indikator neu gezeichnet wird.
Es gibt keine Verzögerung, da es sich im Allgemeinen nicht um ein Muwink handelt. Das Problem der Minimierung der Funktion für eine gegebene Reihe wird gelöst. Wenn sich die Reihe bewegt und die Länge der Reihe gering ist, wird sie natürlich neu gezeichnet, wenn neue Informationen auftauchen, insbesondere wenn es Spitzen gibt. Beschreibung des Filters unter http://en.wikipedia.org/wiki/Hodrick-Prescott_filter
Im Prinzip ist diese Funktion in MATLAB, wenn ich mich nicht irre, kann sie mit dem Matlab-Compiler zu einer DLL gemacht werden. Erstellen Sie daher einen Indikator, der diese Dll anspricht.
Ich glaube, die Welt ist einfacher als mit einem dll.
Hier ist die Funktion, die wir minimieren müssen, um diesen digitalen Filter zu erstellen:
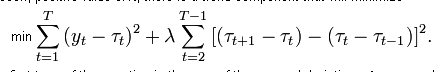
Wir sehen, dass der Filter in dieser Formulierung nur mit historischen Daten arbeiten kann, denn um den Wert der Trendlinie zum aktuellen Zeitpunkt zu berechnen, müssen wir nicht nur die vorherigen Werte dieses Trends kennen, sondern auch einen Schritt voraus t[i+1]. Ein solcher Filter zeigt in der Geschichte die exakte Übereinstimmung der glatten Kurve mit dem Kotir (dies hat der Autor im ersten Beitrag als Beweis angeführt), während es am rechten Rand des Kotirs zu einer unglaublichen Überzeichnung kommt.
Hier ist, was ich sonst noch im Internet ausgegraben habe:
Ich konnte kein fertiges Rezept für den Bau dieses Filters finden. Nehmen wir ein Funktional für den rechten Rand von BP und erstellen wir es selbst (obere Gleichung).
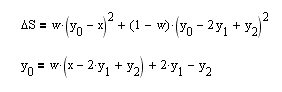
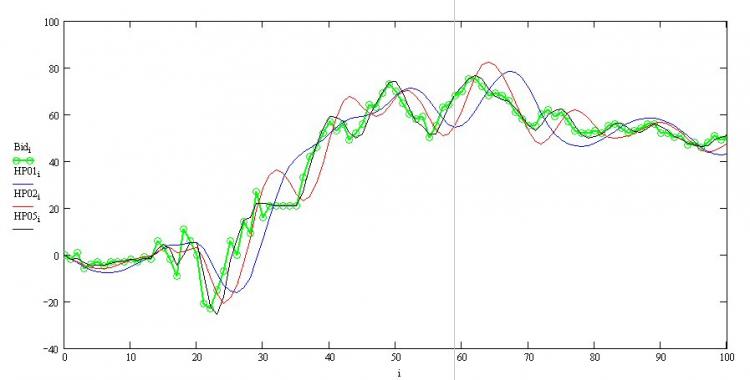
Leiten wir ihn nach dem Parameter y[0] - aktueller Wert ab und setzen ihn mit Null gleich, so erhalten wir sofort einen wiederkehrenden Ausdruck für den erforderlichen HP-Filter (untere Gleichung). Wir wollen sehen, wie die Glättungseigenschaften des Filters vom Glättungsparameter w abhängen:
Hier ist die grüne Linie cotier, die schwarze Linie ist w=0,5, usw. Sie können sehen, dass alles richtig funktioniert - es gibt eine unvermeidliche Phasenverzögerung, die umso größer ist, je stärker das Antialiasing ist, und der rechte Rand wird nicht neu gezeichnet. Jetzt können wir es auch in MQL codieren.
//+------------------------------------------------------------------+
//| Moving Average HP.mq4 |
//| Code by Neutron |
//+------------------------------------------------------------------+
#property indicator_chart_window
#property indicator_color1 Blue
#property indicator_width1 3
extern double w=0.1;
int Start,i,m;
double MA[5000],Y[5000];
int start()
{
Start=5000;
MA[Start]=Open[Start];
MA[Start-1]=Open[Start-1];
for (i=Start-2;i>=0;i--) MA[i]=w*(Open[i]-2.*MA[i+1]+MA[i+2])+2.*MA[i+1]-MA[i+2];
}
int init()
{
SetIndexStyle(0,DRAW_LINE);
SetIndexBuffer(0,MA);
return(0);
}
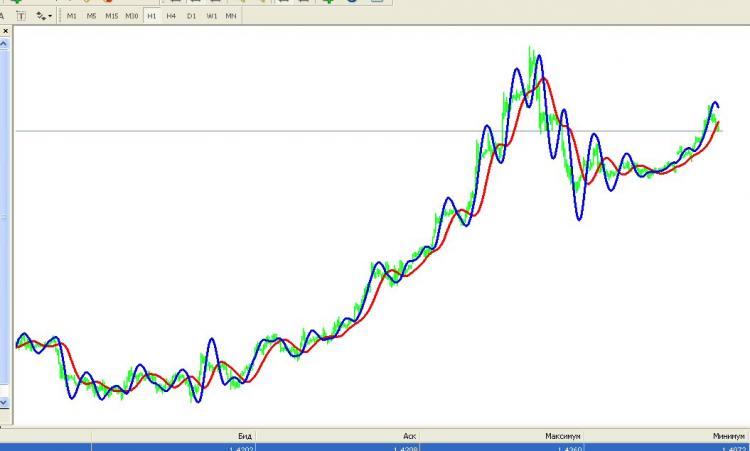
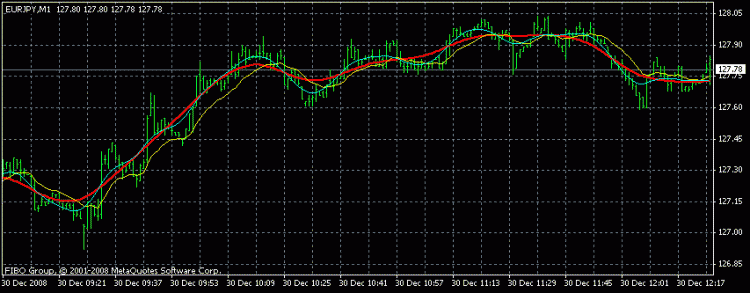
Das Ergebnis sieht folgendermaßen aus:
Blau ist HP, grün ist cotier, rot ist ein Watterout-Filter 2. Ordnung (zum Vergleich).
Dieser Filter versucht nämlich, lineare Trends ehrlich zu erfassen. Schauen Sie sich die Funktionalität am Anfang des Beitrags an - sie zeigt, dass zusätzlich zur Minimierung der Abweichung vom Kotir (erste Summe) auch die zweite Ableitung (zweite Summe) minimiert werden muss! Und schließlich ist die zweite Ableitung der Linie Null, und die Anforderung, sie zu minimieren, ist gleich der Anforderung, das Streben nach der Trendlinie für einen beliebigen Eingangsvektor von Daten zu maximieren. Der Ansatz hat mir gefallen.
P.S. Es ist interessant, wenn man in dem Ausdruck für das Funktional die Minimierung der ersten Ableitung (die obere Gleichung) anstelle der zweiten Ableitung verlangt, erhält man eine sich verändernde Rekursionsformel für den exponentiellen Durchschnitt EMA (die untere Gleichung):
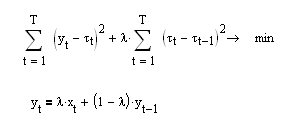
Es stellt sich heraus, dass der exponentielle Durchschnitt die glatteste aller möglichen Manöver ist!
Es stellt sich heraus, dass der exponentielle Durchschnitt die glatteste aller möglichen Muwings ist
Ja, es gibt einen Artikel zu diesem Thema.
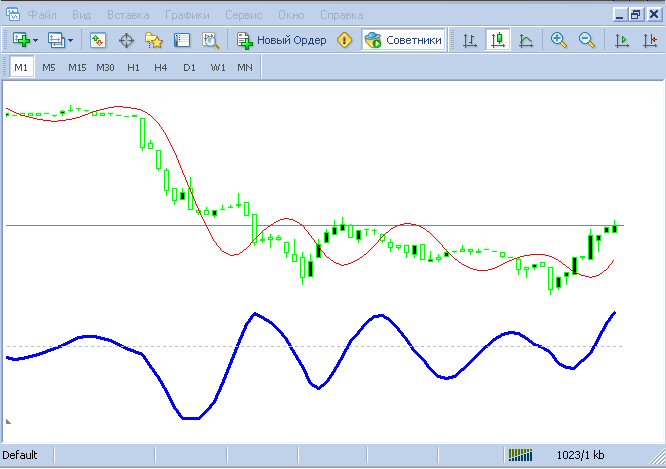
Haven nicht auf den Artikel getan, aber durch die Entwicklung der gleichen Idee der Ema Glätte können Sie gute Glätte zu bekommen:
Blau - EMA15 mit einer Verzögerung von 5.
Rot - glattere MA mit der gleichen Verzögerung.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

Hallo, liebe Programmierer!
Wer wird sich wohl der einfachen Aufgabe stellen, einen Indikator zu schreiben? Ich muss einen Indikator schreiben, der die Reihen mit dem Hodrick-Prescott-Filter filtert. Die Funktion ist in MATLAB verfügbar, wenn ich mich nicht irre, kann sie mit dem MATLAB-Compiler in eine DLL umgewandelt werden. Dementsprechend müssen wir einen Indikator erstellen, der sich auf diese Dll bezieht. Bei der Eingabe sollten folgende Parameter eingegeben werden: Länge der Reihe, Glättungsparameter. Die Ausgabe besteht aus einer Trendkomponente (die im Diagramm eingezeichnet wird) und einer zyklischen Komponente (Oszillator).
Ich kann es nicht selbst machen, ich kenne den MATLAB Compiler und MQL4 nicht.
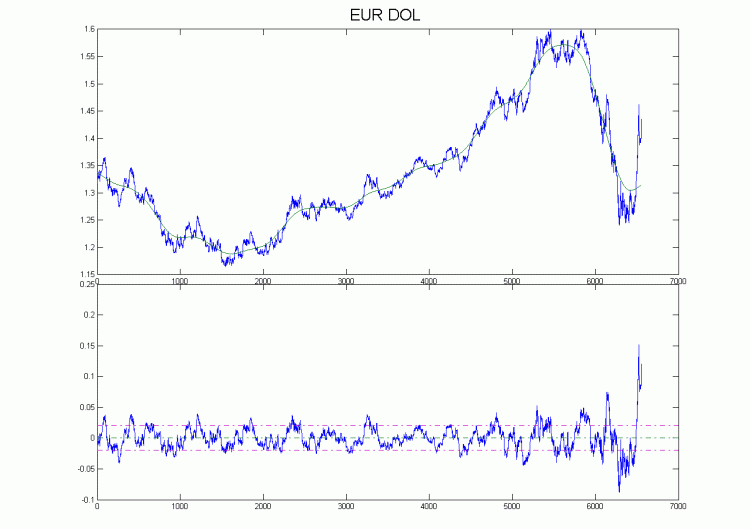
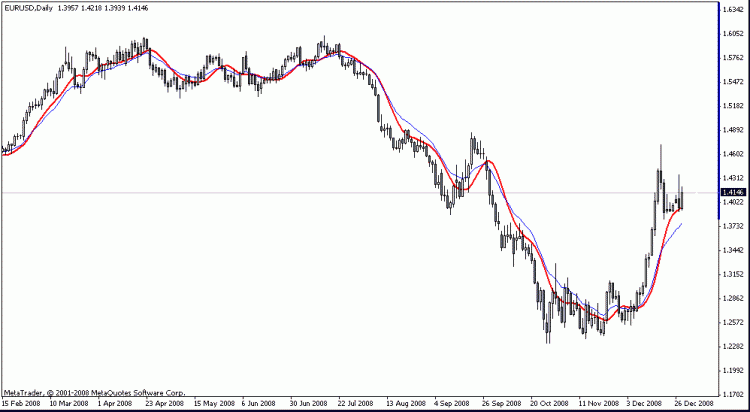
Ich habe eine Zerlegung für Eurodollar H4 auf dem Chart. Wie fast durchgängig in der Geschichte zu beobachten war, bestand die Besonderheit der Preisbewegung darin, dass sich der Preis nach dem Durchbrechen des Trends in einem Abstand bewegte, der der Differenz zwischen dem vorherigen Extremwert und dem Trend entsprach, kurz gesagt, die Amplitude war fast dieselbe. Die Ausnahme sind die jüngsten Daten, aber da ist es extrem. Grundsätzlich sollte ein solcher Indikator neu gezeichnet werden, wenn die Anzahl der Datenpunkte klein ist; wenn sie jedoch erhöht wird, z. B. auf 2000, treten keine Probleme mit dem Neuzeichnen auf.