Combinatoria y teoría de la probabilidad en el trading (Parte I): Fundamentos

Contenido

• Introducción
• ¿Cómo puede ayudar la teoría de probabilidad a analizar el mercado?
• Matices de la teoría de probabilidad aplicada al comercio manual y automático
• Árbol de probablidad e hipótesis
• Sobre los fractales
• Esquema de Bernoulli
• Creando el primer fractal
• Resumiendo
• Conclusión

Introducción

A nuestro juicio, el lenguaje de la teoría de probabilidad es capaz, como ningún otro, de descubrir al tráder un nivel de comprensión completamente distinto de los procesos que suceden dentro del mercado. Una vez dominadas las sutilezas y matices de la teoría de probabilidad, comenzaremos a pensar en categorías completamente diferentes. Parece que (o alguien dijo que debería ser así) ya no causarán en nuestro cerebro reflejos falsos o un deseo de comerciar a una velocidad vertiginosa en una cuenta real. Por otro lado, resulta comprensible que este enfoque resulte ajeno para muchos, principalmente porque mucha gente vive con un paradigma completamente diferente que les resulta cómodo. Queremos sacudir un poco la conciencia del lector y mostrarle un enfoque real y correcto del trading. Los más importante de todo deberían ser los números y solo ellos, y no los "tal vez", "si", "me parece" y "y si".

¿Cómo puede ayudar la teoría de probabilidad a analizar el mercado?

Merece la pena señalar que durante mucho tiempo, el propio autor estuvo muy involucrado en las ciencias técnicas, y que la teoría de probabilidad suponía un auténtico tormento. Además de su dificultad, el principal escollo era no comprender bien todas las posibilidades que brindaba. Una ventaja indiscutible es la amplitud ilimitada de sus capacidades, que depende solo de nuestro ingenio y diligencia y, por supuesto, de nuestro intelecto. Querríamos señalar que, después de años de estudio de disciplinas técnicas, a nuestro juicio, queda claro que la inteligencia no consiste en la velocidad de ejecución del mismo tipo de operaciones o de la propia atención, sino de la muestra la flexibilidad de la mente. Si tomamos como ejemplo las matemáticas diferenciales, la teoría de los campos vectoriales y escalares, e incluso el álgebra escolar, hay en todas partes un cierto conjunto de reglas o recomendaciones que nos permiten resolver casi cualquier problema. Tan pronto como la tarea comienza a ir más allá del estándar, nuestro cerebro se bloquea y no entiende qué hacer. En la teoría de la probabilidad hay muchísimos momentos así, y precisamente por ello la solución a muchos problemas solo puede lograrse con enfoques completamente distintos. En otras palabras, la inteligencia solo se puede desarrollar con tesón y voluntad inquebrantable para resolver el problema que sea, y ​​la teoría de la probabilidad nos ayudará con esto.

Dentro de la teoría de probabilidad, se describen conceptos fundamentales del trading, tales como la esperanza matemática, las probabilidades posibles de varios eventos, varios valores promediados, porcentajes y mucho, mucho más. La teoría de probabilidad nos enseña que no existe un sistema comercial perfecto, y que cada sistema conlleva sus propios riesgos. Solo podemos elegir un sistema comercial cuyos riesgos no nos causen molestias. Sin embargo, lo más importante es interpretar correctamente estos riesgos. En otras palabras, nos estamos alejando de un lenguaje impreciso de sensaciones o aproximaciones visuales hacia criterios cuantitativos claros. Obviamente, también necesitamos elementos visuales, pero estos funcionan mejor en conjunto con los indicadores cuantitativos. Resulta imposible describir todos estas sutilezas y matices en un artículo, pero sí que podemos ver algunas cosas interesantes. Estamos seguros de que incluso aquellos que están familiarizados con las matemáticas encontrarán algo útil para sí mismos.

Matices de la teoría de probabilidad aplicada al comercio manual y automático

Para utilizar correctamente la teoría de probabilidad en el análisis del mercado, primero debemos familiarizarnos con los eventos y sus probabilidades. Un evento es un conjunto de resultados que cumplen con ciertos criterios o se agrupan según algún criterio en un conjunto individual. Entendemos por resultado un cierto elemento elemental que resulta igual a todos los demás en un grupo dado. Hablaremos de "grupo" refiriéndonos a todos los posibles resultados de un proceso. No importa tanto qué tipo de proceso sea, cómo sea su física o cuánto tiempo requiera dicho proceso, lo más importante es que, una vez transcurrido plenamente el proceso, obtendremos algún resultado o algo que no se encontraba allí antes de que el proceso se completara. De hecho, precisamente los resultados que se relacionan con nuestro evento serán nuestro evento, lo único es que, para percibirlos de forma más cómoda, los combinaremos en un solo objeto. Podemos representar todo lo dicho de forma condicional en una figura:

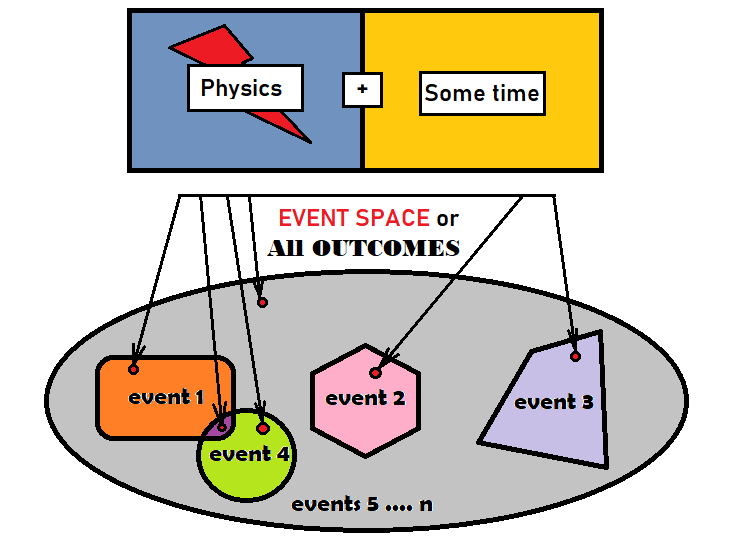
La elipse gris aquí representa todos los resultados, y generalmente se conoce en matemáticas como "espacio de eventos". Esto no significa que el espacio de eventos tenga una forma geométrica: solo un plano resulta lo bastante adecuado para describir estos conceptos. Hemos dibujado 4 eventos diferentes dentro de la elipse. Como podemos ver en la figura, hay un pequeño punto rojo dentro de cada evento. De hecho, estos puntos pueden suponer un número limitado o un número infinito, todo depende del proceso que estemos trabajando. En la figura también tenemos dos eventos que se cruzan. Estos eventos se denominan eventos "simultáneos". Se llaman así porque hay resultados que pertenecen a ambos eventos. El resto de los eventos son "no-simultáneos" porque están ubicados en diferentes partes de la elipse y no se cruzan geométricamente. El resto del área gris se puede considerar el último evento, o también podemos dividirla en partes más pequeñas hasta que no queden áreas grises.

Cada evento debe tener al menos un número correspondiente, que generalmente se llama "probabilidad". La probabilidad indica la frecuencia con la que el evento seleccionado aparece en el proceso de repetición de un mismo proceso, si pudiéramos reproducir la misma experiencia indefinidamente. Hay dos tipos de espacios de eventos:

1. Con un número finito de posibles resultados
2. Con un número infinito de posibles resultados

En el caso del número finito de posibles resultados, podemos calcular la probabilidad de la siguiente manera:

• P = S/N , donde S es el número de resultados que se ajustan a los criterios del evento y N es el número total de todos los resultados en el espacio de eventos

En algunos casos, cuando el número de resultados en un espacio de eventos concreto es infinito, también podemos determinar esta probabilidad, por ejemplo, usando integrales. Concretamente, en el caso de nuestro dibujo, los valores "S" y "N" pueden ser reemplazados por el área de sus formas geométricas.

No siempre resulta posible definir claramente qué es el espacio de eventos, al igual que no siempre es posible determinar concretamente cuántos resultados contiene y qué tipo de física describen. Estas representaciones gráficas solo sirven para ayudar a realizar analogías a nuestro cerebro, para que este no comience a trabajar con alguna geometría y no intente entender el "qué" y el "por qué", sino que se acostumbre a la idea de que trabajamos exclusivamente con las probabilidades y los números adicionales que se corresponden con estas probabilidades. Los eventos también se pueden llamar "estados". Si usamos la lógica de los estados, resultará que la probabilidad no es más que la frecuencia con la que ocurre un cierto estado como resultado de repetir los mismos experimentos. 

Si continuamos con la lógica de las áreas de las figuras, tendremos que la suma de las áreas de todas las figuras incluidas en la elipse es exactamente igual al área de esta. Si pasamos ya al lenguaje de las matemáticas, entonces el área será el número de resultados que entran allí. Entonces tendremos que:

• N = S[1] + S[2] + ... + S[n]
  
• S — es el número de resultados de un evento en particular
• N — representa todos los resultados del espacio de eventos

Si dividimos ambos lados de la igualdad por el valor "N", obtendremos una relación interesante y muy importante, subyacente a toda la teoría de probabilidad:

• 1 = S[1]/N   +   S[2]/N   +   ...   +S[n]/N

Solo queremos aclarar que esta relación funciona solo para aquellos eventos que son inconsistentes, porque si los eventos son no-simultáneos, entonces las áreas de las figuras comienzan ya a superponerse, y su área total será mayor que el área de la figura elíptica original. Todos hemos montado un puzle en la infancia, así que tenemos claro que el área de todas las piezas del rompecabezas es exactamente igual al área de la imagen que obtenemos al final. En este caso, cada pieza del rompecabezas representará uno de los eventos. Continuando en esta línea, estará claro que todas estas fracciones no son más que las probabilidades de eventos específicos:

• 1  = P[1]   +   P[2]   +   ...   +P[n]

De esta relación surge el término "grupo completo de eventos". Un grupo completo de eventos supone la totalidad de todos los eventos no-simultáneos que forman un cierto espacio de eventos. En el caso del puzle, el grupo completo serían todas las piezas del mismo. La probabilidad total de todos estos eventos debe ser necesariamente igual a uno, lo que significa que uno de estos eventos deberá ocurrir necesariamente como resultado del experimento. No sabemos cuál, pero lo averiguaremos a partir de los resultados del experimento.

Si pensamos detenidamente, podremos comprender que podrá actuar como evento cualquier conjunto de resultados del espacio de eventos elegido. Esto significa que podremos montar un grupo completo con todas las formas y combinaciones posibles. Si tenemos un número finito de resultados, puede haber un número limitado de estas combinaciones; si tenemos un número infinito de resultados, el número de combinaciones será infinito. Si ya sabemos que el número de resultados es igual a infinito, los matemáticos comenzarán a considerar ese concepto como una "magnitud aleatoria". En algunos casos, resulta incluso conveniente operar con variables aleatorias, porque la tarea nos permite hacerlo. Una variable aleatoria es una forma ligeramente diferente de describir el espacio de eventos. En este caso, el resultado será un conjunto claro de uno o más números: podemos decir que se trata de un vector. En el marco de este modelo de análisis, se introduce el concepto de "densidad de probabilidad". 

Creo que vale la pena considerar estos conceptos, al menos de manera superficial, ya que los necesitaremos en el futuro al analizar el resto del material, así como para alcanzar algún tipo de comprensión por nuestra parte. La densidad de probabilidad es una función que describe todo el espacio de eventos a la vez. La dimensión de esta función es exactamente igual a la cantidad de números requeridos para describir cada resultado en un espacio de eventos dado. Por ejemplo, si analizamos el problema de disparar a un objetivo en un campo de tiro, la dimensión de esta función será igual a dos, porque el objetivo es plano y representa un espacio bidimensional. En este caso, las características de un resultado particular serán las coordenadas X, Y. Estos números suponen nuestras variables aleatorias, y ahora podemos escribir:

• R = R(X,Y)
• R — es la densidad de probabilidad de que una bala alcance el punto con las coordenadas (X, Y)

Las propiedades de esta función son tales que la integral completa de menos a más infinito sobre todas las variables de esta función será igual a uno, que, de hecho, refleja la misma identidad que estaba arriba. Las probabilidades aquí están determinadas solo por integrales en el área donde se representa la función y nada más. Varios eventos componerse de área integradas por partes; si lo deseamos, podemos describir estos eventos como deseemos, porque su número es igual a infinito. Dentro de este artículo, dicha definición resultará suficiente para que entendamos reflexiones posteriores: a nuestro juicio, no debemos profundizar más, porque entonces estaremos hablando de cosas mucho más serias, absolutamente inútiles en el marco de nuestras tareas.

Hablemos un poco más sobre los eventos simultáneos. Estos eventos también son muy importantes para alcanzar una comprensión general de la imagen en su conjunto. Está claro que con los eventos no-simultáneos todo debería resultar bastante simple, pero con los eventos simultáneos, todo es más complicado. Dentro del marco de la teoría de la probabilidad, tenemos que tratar con cosas como la combinación o división de eventos, pero no necesitamos saber qué aspecto tendrá esta división o combinación: solo nos interesan las probabilidades que se obtendrán como resultado de estas transformaciones. Para ello se introduce el concepto de suma, y producto de eventos, así como la operación de inversión. Estas operaciones no significan lo mismo que en las matemáticas ordinarias y, además, están diseñadas para trabajar solo con probabilidades. Las probabilidades de eventos simultáneos no se pueden sumar, porque en este caso se violará la integridad del grupo. En general, estas 3 operaciones sobre eventos iniciadores pueden describir todos los eventos posibles que se pueden componer usando partes de los eventos iniciales. Usando el ejemplo de dos eventos simultáneos, podemos mostrar qué aspecto tendrá en un plano:

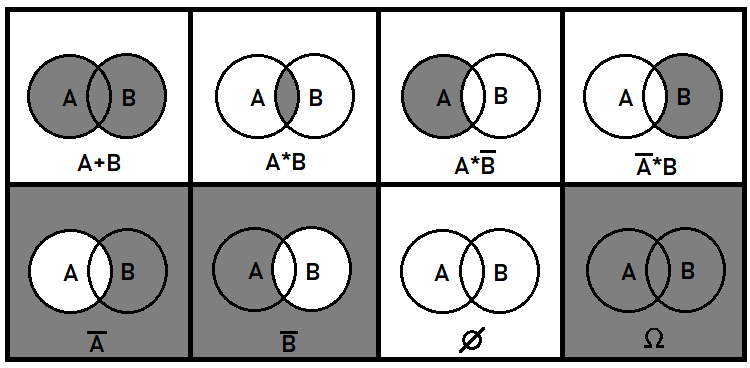
De hecho, podríamos pensar en operaciones algebraicas adicionales, pero estas pueden estar compuestas por las ya presentadas. Por ejemplo, la división booleana equivale a la tercera y cuarta situaciones de la figura, ya que la división es equivalente a multiplicar por el inverso del evento seleccionado. En general, si hablamos con rigor, los dos primeros casos bastan para describir todos los eventos posibles que se pueden construir partiendo de las partes de los eventos iniciales. Si hay más de dos eventos simultáneos, las cosas se vuelven mucho más complicadas. En este artículo, no operaremos aún con eventos simultáneos, sino solo con eventos no-simultáneos.

Las matemáticas de mercado se basan principalmente en el concepto de "paseo aleatorio". Después de considerar este concepto, podremos generalizar estos datos en el caso de que haya patrones. Empezaremos suponiendo que abrimos una posición con un stop loss y un take profit equidistantes respecto al precio de apertura. Si no tenemos en cuenta los spreads, las comisiones y los swaps de estas posiciones e imaginamos que la posición se ha abierto gratuitamente, entonces, a nuestro parecer, resultará obvio para todos que si comerciamos aleatoriamente en diferentes direcciones y en diferentes puntos del gráfico, la relación beneficio/pérdidas tomará un valor igual a uno. En otras palabras, realizando operaciones sin fin, el número de posiciones rentables resultará exactamente igual al número de posiciones perdedoras. De este hecho, podemos deducir que obtendremos cero beneficios, no importa cuánto tiempo comerciemos; lo que es más, si restamos las pérdidas de los spreads, comisiones y swaps, resultará que estamos perdiendo.

Muchos podrán pensar, ¿por qué deberíamos saber qué es un paseo aleatorio y por qué necesitamos en general conocer las matemáticas de este proceso, si de todas formas ya sabemos que estamos en números rojos? El paseo aleatorio puede ayudarnos a calcular las probabilidades de varios eventos, tales como el cierre con stops asimétricos o el precio medio que se desplazará el gráfico en un determinado intervalo de precios. Además, también puede ser de ayuda al calcular el tiempo de expiración de una posición, así como otros indicadores útiles que, si bien no responden a nuestra pregunta sobre dónde entrar y dónde salir, definitivamente nos servirán en la evaluación de riesgos o en cuestiones referentes a la maximización o minimización de valores tales como el beneficio y las pérdidas.

Árbol de probablidad e hipótesis

Un ejemplo muy útil para desarrollar nuestros lóbulos frontales serían los árboles de eventos o árboles de probabilidad. Este tema se origina en el "esquema de Bernoulli", porque se encuentra en el corazón de todos los árboles de probabilidad. Este diagrama analiza las cadenas de eventos no-simultáneos que se suceden uno tras otro. Pero antes de pasar al análisis, hablaremos de la "fórmula de probabilidad total". Mediante el estudio de esta importantísima construcción se puede llegar al esquema de Bernoulli, y ya desde el esquema, a los árboles de probabilidad. Esta fórmula tiene el aspecto siguiente:

• P(A) = Suma (0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] - probabilidad del evento А
• P(H[i]) — probabilidad de la hipótesis "H[i]"
  
• P(A|H[i]) — probabilidad de que el evento A ocurra dentro de la hipótesis "H[i]"

También querríamos decir que cuando se trata de probabilidades, resulta mejor ceñirse a la regla de escribir estas como hipótesis. Por ejemplo, esta anotación "P(H[k]|H[i]) significará lo siguiente:

1. Probabilidad del evento "H[k]" calculada en relación con el espacio "H[i]"

Entonces, queda claro de inmediato qué evento se considera un espacio y qué evento está anidado. El asunto es que, en la práctica, cada evento supone un espacio de eventos diferente más pequeño, y dentro de él, pueden existir otros eventos anidados, y así sucesivamente. Y, por ejemplo, esta entrada "P(H[i])" puede, según esta lógica, escribirse así:

• P(H[i]|O) — porque esta probabilidad se considera respecto a "O".
  

Ahora, vamos a analizar la fórmula de la probabilidad total por partes, para entender mejor qué se esconde en ella. Resulta bastante difícil comprender de entrada lo que sucede en esta fórmula, pero seguro que pronto nos aclararemos. Comenzaremos reescribiendo esta fórmula de una forma ligeramente distinta:

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — área de un segmento específico de intersección de la hipótesis H[i]
• N [i] - área de toda la hipótesis H[i] (incluida S[i])
• O  — todos los resultados, o el área de toda la elipse

Tras realizar algunas transformaciones mínimas (hemos multiplicado el numerador y denominador de las fracciones por el valor  "N[i]"), podemos ver en ella las probabilidades presentes en la fórmula original:

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Para una mejor asimilación, podemos representar todo gráficamente de esta forma:

 

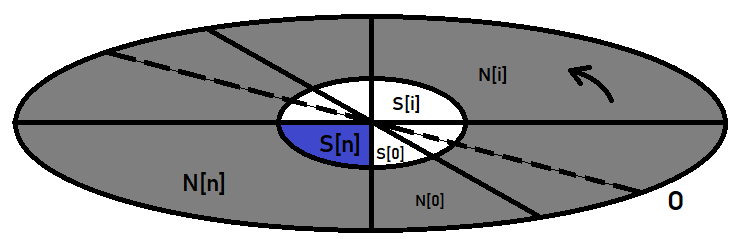
La elipse exterior aquí juega el papel del espacio de eventos, y la central, el papel del evento cuya probabilidad estamos buscando. Si imaginamos todo como un reloj, entonces, tras dibujar el diámetro de la elipse y girarlo en el sentido opuesto a las agujas, cortaremos nuestra elipse en segmentos, que son las hipótesis. "Hipótesis" es simplemente un nombre especial para los eventos, pero en realidad son los mismos eventos, en nada diferentes del que estamos buscando.

Esta fórmula contiene un caso especial que nos ayudará con la construcción del esquema de Bernoulli. Imaginemos que la elipse central se encuentra al completo dentro de una de estas hipótesis. Entonces resultará que todos los términos de esta suma relacionados con el resto de hipótesis se pondrán automáticamente a cero, ya que la probabilidad de que suceda el evento "A" en el marco de estas hipótesis es imposible o igual a cero, que es lo mismo, lo cual reduce estos términos a cero. Como resultado, tendremos que:

• P(A) = P(H) * P(A|H)
• H  — es la probabilidad de que se dé exactamente la hipótesis dentro de la cual se ubica el evento seleccionado, al completo.

Si vamos más allá, entonces podemos suponer: pero ¿y si el evento "A" también se llama hipótesis? ¿Y por qué no? Una hipótesis es un evento, y esto significa que cualquier evento es una hipótesis. Ahora, supongamos que hay otro evento "B" que ya está dentro de "A", entonces, resultará que "A" es una hipótesis en relación con "B", y la fórmula anterior se aplicará a estos dos eventos:

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Sustituyendo allí la relación anterior en lugar de  "P(A)", podemos ver un cierto patrón en la construcción de una fórmula general para cualquier número de hipótesis o eventos anidados entre sí. ¿Y por qué necesitamos esto?, se preguntará el lector. Porque este es un prototipo directo de la fórmula de Bernoulli que analizaremos un poco más tarde; por ahora, analizaremos algo muy curioso.

Sobre los fractales

Si respetamos la lógica anterior, resultará que si P (A) + P (B) = 1, entonces este será un grupo completo de eventos, y resultará que el grupo completo se puede ensamblar a partir de dos cadenas arbitrarias de hipótesis anidadas unas en otras. Pero estas hipótesis pueden resultar conjuntas, y si necesitamos que todas las hipótesis anidadas posibles sean no-simultáneas con las hipótesis de otras cadenas, esto provocará automáticamente que todas las cadenas sean inconsistentes con otras cadenas en el espacio de eventos dado. Si pensamos detenidamente en qué aspecto tendrá gráficamente, obtendremos una formación muy interesante:

Esta formación se llama "Fractal", porque resulta imposible construir tal estructura hasta el final, se puede construir indefinidamente. En nuestra imagen, está construido solo a 3 niveles de profundidad. Los rectángulos azules aquí representan el final de una cadena de probabilidades individual. Lo más interesante es que si sumamos las probabilidades de todas estas cadenas, formarán un grupo completo de eventos.

Para describir estos fractales, resulta que las "combinaciones" son muy adecuadas. Las combinaciones se construyen usando como base el concepto de "factorial". También existe el concepto de "permutación": según la jerarquía, este concepto se encuentra entre el factorial y la combinación. La fórmula de permutación se deriva de la fórmula factorial, y la fórmula de permutación implica el concepto de combinación. Vamos a mostrar las siguientes fórmulas:

• n! - factorial del número "n"
• P(n,k) = n! / ( n - k )!  — permutaciones de elementos "N" por elementos "K"
• С(n,k) = n! / ( k! * ( n - k )! )  — combinaciones de "N" elementos por elementos "K"

Creo que para nadie es un secreto que el factorial es el producto de todos los números naturales que comienzan con "1" y terminan con el número "n", mientras que "0! = 1". = 1". Es decir, el factorial de cero es igual a uno; en este caso, se trata solo de una excepción a la regla, pero, en la práctica, no se ven casos donde esta excepción interfiera con los cálculos o complique los algoritmos, más bien al contrario.

Las permutaciones resultan un poco más complicadas. Imaginemos que tenemos un mazo de cartas con una cierta cantidad de estas. Se nos ha ocurrido un experimento simple: tenemos que barajar el mazo y quitar varias cartas de una manera completamente arbitraria y colocarlas sobre la mesa en el orden en que las hemos sacado del mazo. Entonces, las permutaciones solo suponen el número de todos los resultados posibles de una experiencia dada, mientras que el orden de las cartas también se considera un identificador único de un resultado en particular. Está claro que esto se aplica no solo a los experimentos con cartas, sino a cualquier cosa, incluyendo piedras o lápices.

La primera carta se puede sacar del mazo de "n" formas, la segunda de "n-1" formas, ya que la primera carta que se ha extraído del mazo ya no se encuentra en el mazo, y así sucesivamente hasta "n-k-1". Resulta que para obtener el número de todas las permutaciones posibles, deberemos multiplicar todos estos números de "n-k-1" a "n". Y, obviamente, esto nos recuerda mucho al factorial. Si tomamos "n!" y lo dividimos por los últimos factores "n-k", obtenemos exactamente el producto que había originalmente, ¡y este producto es exactamente igual a "(n-k)!". Así es como obtenemos la famosa fórmula de permutación.

La fórmula de combinación resulta un poco más complicada, pero también es muy fácil de deducir. Ahora, vamos a pensar un poco sobre si hemos escrito todas las permutaciones posibles, pero, en esta ocasión, no nos importará el orden de sus elementos, solo será importante qué cartas han entrado en este conjunto. Ahora necesitamos encontrar el número de todos esos casos en los que hemos obtenido un conjunto de cartas ligeramente diferente al de todos los demás. De hecho, cada permutación contiene ya uno de estos conjuntos únicos, pero no los necesitamos todos. En esta ocasión, cambiaremos ligeramente la lógica del pensamiento, intentando recopilar todas las permutaciones de todas las combinaciones posibles: luego resultará que si tomamos una combinación, no importará cómo reorganicemos los elementos en ella: cada una de esas permutaciones será única. Además, si tomamos todas esas combinaciones únicas y hacemos todas las posibles permutaciones con los elementos en ellas, obtendremos todas las posibles permutaciones, y resultará que:

• P(n,k) = C(n,k) * P(k,k)

El número de todas las permutaciones únicas dentro de una combinación es exactamente igual a "P(k,k)", porque necesitamos recopilar de las variantes "k" todas las permutaciones posibles para las mismas variantes "k". A partir de aquí, podemos ver que dividiendo ambos lados de la ecuación por "P(k,k)", podemos obtener la fórmula de combinación deseada:

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

Tanto las permutaciones como las combinaciones se usan mucho en diversos problemas de la teoría de probabilidad, pero si hablamos de aplicación práctica en el trading, son las combinaciones las que nos resultarán de gran utilidad. Se usan para construir funciones fractales con multitud de propósitos. Quizás sería más correcto llamarlas recurrentes, pero, por alguna razón, llamamos a estas funciones "fractales", probablemente porque son realmente fractales: en ellas no existe simplemente recursividad, sino un árbol completo de llamadas.

Esquema de Bernoulli

Antes de comenzar a analizar estas funciones fractales, deberemos echar un vistazo a esta famosa fórmula. Imaginemos que tenemos una cadena de experimentos idénticos que tenemos que repetir varias veces. Como resultado de la experiencia, un evento determinado deberá aparecer, o no, con cierta probabilidad. Además, supongamos que queremos encontrar la probabilidad de que en una cadena de "n" experimentos, nuestro evento aparezca exactamente "k" veces. La fórmula de Bernoulli puede responder a esta pregunta:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)   — fórmula de Bernoulli
  
• p  — probabilidad de obtención de un evento en el resultado de una única experiencia
• q = 1 - p   — probabilidad de que un evento no ocurra como resultado de la experiencia

Recordemos la fórmula que obtuvimos para las cadenas probabilísticas; podemos ampliarla para el caso en que se da una longitud de cadena aleatoriamente grande:

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n  — número de segmentos de la cadena
• O  — conjunto completo de resultados, también se puede marcar como H[0]

Esta fórmula calcula la probabilidad de que tenga lugar exactamente la cadena de hipótesis necesaria. Visualmente, podemos representar esta fórmula de la manera que sigue:

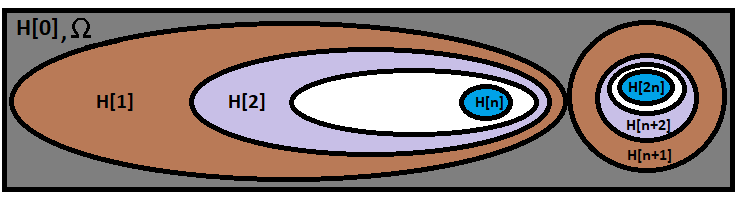
En la primera y más grande de las elipses, se encuentra nuestra fórmula, mientras que la otra cadena, dibujada a su lado, resulta inconsistente con nuestra cadena; sin duda, simboliza alguna otra rama de una combinación diferente. Hay exactamente tantas ramas como opciones para calcular las combinaciones en nuestra fórmula. Lo único es que no debemos confundir las combinaciones en sí mismas con las opciones para calcular las combinaciones. El número de opciones para calcular combinaciones es:

• n+1 (las combinaciones de "0" resultados exitosos también se consideran)
• n  — número de pruebas independientes en una cadena de experiencias

Ahora, imaginemos que las probabilidades de todas estas hipótesis son iguales a "p" o "q". Entonces la fórmula se simplificará:

• P(n) = Pow(p,k)*Pow(q,n-k)
• k  — cuántos factores iguales a "p" están presentes en el producto
• n-k  — cuántos factores iguales a "q" están presentes en el producto

La similitud con la fórmula de Bernoulli ya es obvia, solo nos queda la combinación. Pero si lo pensamos con detenimiento, nos quedará claro que las opciones de cadenas con una probabilidad y un número similares de "k" y "n-k" son exactamente iguales a "C(n,k)". Y como todas estas cadenas de probabilidades son inconsistentes entre sí, resultará que la probabilidad de que obtengamos alguna de estas cadenas será igual a la suma de las probabilidades de todas esas cadenas. Y como estas probabilidades son las mismas, podemos simplemente multiplicar la probabilidad de una cadena por su número: así obtendremos nuestra fórmula de Bernoulli:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

Es interesante que esta fórmula pueda extenderse, por ejemplo, a aquellos casos en los que necesitamos encontrar la probabilidad de una combinación de ocurrencia que no está claramente registrada, sino al suceso de un evento "k" o más veces, "k" o menos veces, así como todas las posibles variaciones sobre este tema. En este caso, se dará la suma de las probabilidades de las combinaciones que necesitemos. Por ejemplo, la probabilidad de que el evento ocurra más de "k" veces se calculará de la forma que sigue:

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

También es de vital importancia entender que:

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

En otras palabras, todas las cadenas posibles forman un grupo completo de eventos incompatibles. Otra identidad muy importante es:

• Summ(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

A nuestro juicio, esto es lógico, pues cada segmento de la cadena de probabilidad tiene solo dos estados: "el evento ha sucedido" y "el evento no ha sucedido". El estado en el que el evento no ha sucedido es exactamente el mismo evento, solo que se basa en el hecho de que ha sucedido algo más.

Las combinaciones también poseen una propiedad muy interesante:

• C(n,k) =  C(n,n-k)
  

Podemos llegar a ella calculando lo que es igual a "C(n,n-k)" y comparándolo con "C(n,k)". Después de algunas pequeñas transformaciones, veremos que ambas expresiones son idénticas. Hemos creado un pequeño programa basado en MathCad 15 para poner a prueba todas las afirmaciones anteriores: 

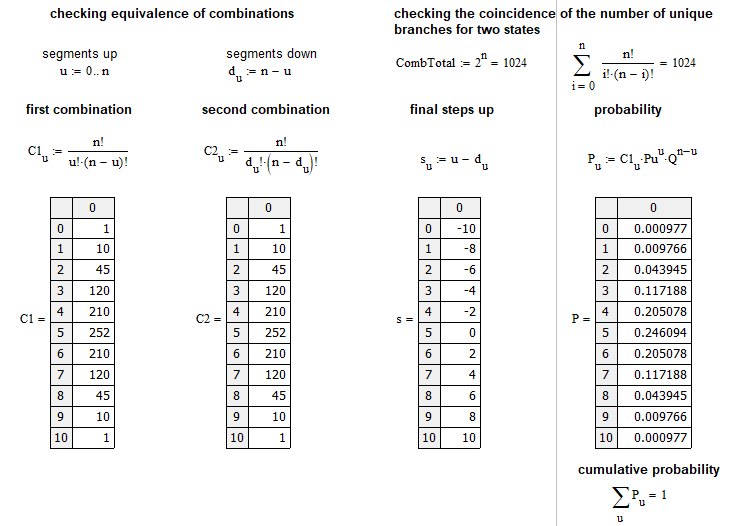
Hemos hecho este jemplo de forma próxima al mercado: calcula la probabilidad de que de "n" pasos el mercado suba "u". Un paso es un movimiento del precio hacia abajo o hacia arriba en un cierto número de puntos en relación con el paso anterior. Gráficamente, la matriz de probabilidades para cada "u" se puede dibujar de la forma siguiente:

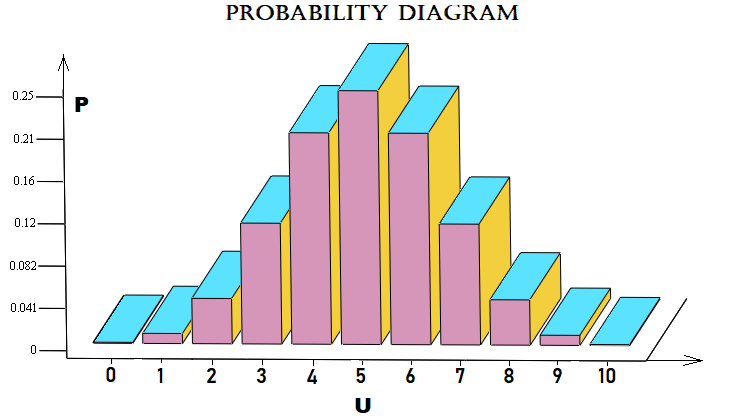
En este caso, por simplicidad, utilizaremos un esquema de Bernoulli con "10" pasos. El archivo se adjuntará al artículo, por lo que el lector podrá experimentar con él. No es necesario aplicar este esquema a los precios: también puede aplicarse a los pedidos y a cualquier cosa.

Creando el primer fractal

Los problemas relacionados con el stop loss y el take profit de las transacciones requieren un análisis aparte. Todo el mundo está interesado en cómo calcular la probabilidad de cierre de una transacción mediante stop loss o take profit cuando los valores de estos se conocen en puntos (distancia respecto al precio actual). Este valor se puede calcular en cualquier momento, incluso si ya no representa el precio de apertura, ya que todo esto depende directamente de los mecanismos de fijación de precios. En este ejemplo, queremos mostrar la prueba de la fórmula usando fractales. En el caso del paseo aleatorio, podemos calcular esta probabilidad de la siguiente forma:

• P(TP) = SL / ( TP + SL ) - probabilidad de activación de un take profit
• P(SL) = TP / ( TP + SL ) - probabilidad de activación de un stop loss
• SL  — distancia en puntos hasta el stop loss
  
• TP  — distancia en puntos hasta el take profit

A nuestro juicio, cualquier lector entenderá que la estas dos probabilidades forman un grupo completo:

• P(TP) + P(SL) = 1
  

Esta fórmula implica automáticamente que, en caso de comercio aleatorio, la esperanza matemática de todas estas estrategias será igual a cero, sin tener en cuenta el spread, la comisión y el swap:

• M =  P(TP) * TP - P(SL) * SL = 0

Este es el caso más simple cuando abrimos con stops fijos, pero, si así lo queremos, podemos generalizar todo esto para absolutamente cualquier estrategia. Ahora, vamos a comenzar a probar esta fórmula usando el propio MathCad 15. Hemos estado trabajando con esto programa durante mucho tiempo, y nos permite realizar cálculos de casi cualquier complejidad, incluso usando programación. En este ejemplo, no solo pondremos a prueba las fórmulas que hemos escrito anteriormente, sino que también veremos el primer ejemplo de construcción de una función fractal. Comenzaremos describiendo esquemáticamente nuestro proceso de movimiento de precios tal como lo representamos. Aquí no podemos utilizar funciones continuas, solo funciones discretas. Para hacerlo, hemos tomado de forma condicional nuestra orden y pospuesto nuestras distancias (stops) hacia arriba y hacia abajo, después de lo cual, hemos dividido estos segmentos en partes con pasos iguales, de modo que cada segmento se ajuste a un número entero de pasos; asimismo, hemos imaginado que el precio se mueve a lo largo de estos pasos. En este caso, resulta obvio que, como los pasos son todos iguales, la probabilidad de un paso en cualquiera de las dos direcciones es exactamente "0.5". Para implementar el fractal correspondiente, necesitaremos una ilustración gráfica:

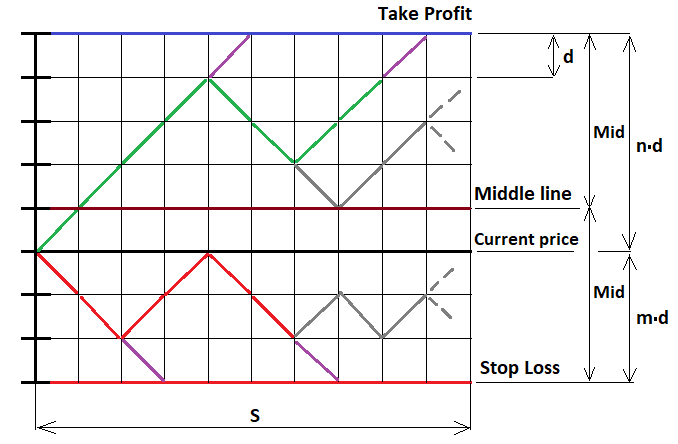
Para resolver este problema, debemos tener en cuenta tres posibles casos de continuación del fractal:

1. Estamos por encima de la línea media  ( U > MiddleLine )
2. Estamos por debajo de la línea media  ( U < MiddleLine )
3. Ahora estamos en el nivel de la línea media (U = MiddleLine)

Como "U", aquí interviene el número total de pasos "u-d" hacia arriba respecto al precio de apertura; si el punto desde el cual vamos a continuar construyendo el fractal está por debajo de este precio, entonces esta magnitud tomará valores negativos de acuerdo con la fórmula. Si estamos en la línea media, entonces el número de pasos que tenemos derecho a dar sin temor a cruzar la línea será exactamente uno menos que "Mid". Pero antes de continuar con la construcción, definitivamente deberemos limitar la construcción del fractal al número de pasos que el precio o las órdenes tienen derecho a realizar. Si el número de pasos supera el requerido, estaremos obligados a interrumpir su posterior construcción. En caso contrario, obtendremos una recursividad infinita de la que será imposible salir, y el tiempo de cálculo será igual a infinito.

En la figura, hemos dibujado varios pasos de color púrpura; en estos puntos, recolectaremos las probabilidades y las sumaremos en una variable común, y luego desplegaremos nuestra cadena hacia arriba o hacia abajo, dependiendo del límite donde se haya apoyado nuestra cadena para que pueda continuar avanzando y construyendo nuevos niveles fractales anidados. En otros puntos, podemos construir libremente niveles fractales completos basados ​​en el esquema de Bernoulli, que hemos analizado anteriormente.

En el caso de que tengamos derecho a construir un árbol basado en el esquema de Bernoulli, primero deberemos determinar el número de pasos que tenemos derecho a hacer, considerando los casos extremos en los que todos los pasos serán exclusivamente hacia arriba o hacia abajo. Para los tres casos, esta magnitud adoptará los valores:

• (n - 1) - U  — cuando nuestra cadena se encuentra ya por encima de la línea central (puesto que un aumento en U implica una disminución en la distancia hasta el límite superior)
• (m - 1) + U  — cuando nuestra cadena se encuentra ya por debajo de la línea central (puesto que una disminución en U implica una disminución en la distancia hasta el límite inferior)
• (floor(Mid)-1)  — cuando nuestra cadena está exactamente en la línea media
• n  — número de segmentos superiores
• m  — número de segmentos inferiores
• floor  — la función descarta la parte fraccionaria del número (quizás esto no sea necesario, lo dejaremos así por ahora)

En este caso, primero deberemos calcular dos magnitudes auxiliares:

• Mid = (m+n)/2  — mitad del ancho del corredor (en pasos)
• Middle = (m+n)/2 - m   — valor "U" para la línea media (en pasos)

Estos valores resultarán útiles en el futuro para describir la lógica de ramificación del fractal. Solo que por ahora construiremos un fractal para los casos "n>=m". Pero estos datos aún resultan insuficientes para construir el fractal correctamente. Para poder construir niveles más profundos del fractal, necesitaremos redefinir "U" para cada nueva combinación del esquema de Bernoulli y transmitir esta a un nuevo nivel fractal. Además, deberemos incrementar correctamente el número de pasos realizados y también transmitirlos correctamente. De la misma manera, tendremos que recopilar la probabilidad de la cadena completa usando los multiplicadores del siguiente nivel fractal y transmitir la probabilidad de la cadena intermedia al siguiente nivel hasta que este proceso finalice con el cruzamiento exitoso del límite necesario. Para comprender todo mejor, hemos creado una ilustración de las tres opciones:

  

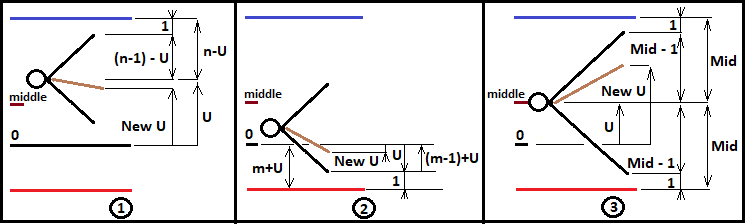
Guiándonos con este diagrama, podremos escribir a qué serán iguales los valores de "NewU" y otros valores auxiliares para cada caso de todos los presentados; analizaremos esto usando el ejemplo de construcción de un fractal para calcular la probabilidad de cruzamiento del límite superior:

Para el caso 1:

Vamos a echar un vistazo a la imagen superior y a describir matemáticamente lo que sucede allí. Esta imagen es un extracto de nuestro programa en MathCad 15. No ofrecemos el listado completo: si el lector lo desea, podrá familiarizarse con él en los anexos al artículo. Mostramos los puntos más importantes porque todo el fractal se encuentra en ellos. También deberemos recordar que el primer rectángulo se encuentra en un bucle y se repite según "i" para describir todas las combinaciones posibles. Esta lógica se puede repetir en el entorno de desarrollo del MetaEditor. Comencemos con la primera ilustración del diagrama. Para definir "NewU", primero necesitaremos definir algunas fórmulas fundamentales que nos ayudarán en esta tarea:

• ( n - 1 ) - U = f — en este caso, la presente magnitud será el número de pasos del futuro árbol de combinaciones (el tamaño es determinado por la distancia respecto al límite más próximo del corredor fractal)
• u + d = f  — la misma magnitud, solo que expresada como el número de segmentos ascendentes y descendentes
• s = u - d  — número de pasos finales, expresado como segmentos descendentes y ascendentes
• u = i  — porque en nuestro programa se repite según "i" (esto necesitamos recordarlo, sin más)

Para calcular todas las magnitudes necesarias, necesitamos expresar "s" a través de "U" e "i": vayamos al grano. Para conseguirlo, solo debemos excluir la variable "d". Primero la expresamos y luego la sustituimos en la expresión para "s":

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

A continuación, usando la expresión encontrada para "s", hallamos "NewU" y todas las cantidades que necesitamos transmitir al siguiente nivel fractal:

• NewU = s + U = -( n - 1 ) + 2*i + 2*U   - nuestra nueva "U" para transmitir al siguiente nivel fractal
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p,( n - 1 ) - U -i)  — nuestra nueva probabilidad de la cadena "P" para la transmisión al siguiente nivel fractal (la obtenemos multiplicando por la probabilidad de un nuevo segmento de la cadena) 
• NewS = S + f = S + ( n - 1 ) - U  — nuestra nueva "S" para transmitir al siguiente nivel fractal

Ahora, echemos un vistazo al rectángulo inferior. En él, procesaremos los casos en los que la cadena de pasos ha llegado al límite superior del corredor. Necesitaremos procesar dos casos aquí:

1. La recopilación de la probabilidad de una cadena que se cruce con el límite (esta acción está subrayada en rojo)
2. Acciones similares para aumentar los nuevos valores que transmitiremos al siguiente nivel fractal

Este caso es muy simple, porque solo hay dos casos posibles:

1. Tocar el límite
2. Virar a partir del límite

Para cada una de estas acciones, no necesitamos un esquema de Bernoulli, porque en este caso solo se da un paso. Por cierto, la probabilidad de un viraje se multiplica precisamente por "(1-p)", porque la probabilidad de cruzamiento es "p", y estos dos eventos tendrían que formar un grupo completo, como ya deberíamos haber entendido de los anteriores cálculos. Naturalmente, se incrementan los pasos en "1", mientras que "U" se disminuye en "1", porque la reflexión está hacia abajo y necesitamos disminuir este valor. Esto es todo lo que necesitamos para mostrar correctamente este caso. Estas reglas resultarán casi idénticas para la construcción de fractales básicos, que necesitaremos para propósitos completamente diferentes.

Para el caso 2:

Para este caso, el cálculo será casi idéntico; la única diferencia será que "f" ya tomará un valor distinto:

• ( m - 1 ) + U = f

Del mismo modo, expresaremos "s" a través de "U" e "i", usando para ello las mismas fórmulas que en el caso anterior:

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

De la misma manera, encontraremos todas las magnitudes que necesitamos transmitir al siguiente nivel fractal:

• NewU = s + U = -( m - 1 ) + 2*i  - nuestra nueva "U" para transmitir al siguiente nivel fractal
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i)  — nuestra nueva probabilidad de la cadena "P" para transmitir al siguiente nivel fractal
• NewS = S + f = S + ( m - 1 ) + U  — nuestra nueva "S" para transmitir al siguiente nivel fractal

El rectángulo inferior aquí resulta casi idéntico al caso anterior, salvo que aumentamos "U" en uno, ya que la reflexión va hacia arriba, y esto significa un aumento en "U". También merece la pena señalar que en este caso no hay recopilación de probabilidades, porque en este fractal no nos interesan los casos de cruzamiento con el límite inferior. Solo nos queda analizar el último caso, en el que la cadena ha entrado en la línea media del corredor.

Para el caso 3:

Definimos "f":

• floor(Mid) - 1 = f

Encontramos "s":

1. d = f - i =  floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Finalmente, encontramos los valores a transmitir al siguiente nivel fractal:

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i)  — nuestra nueva probabilidad de que la cadena "P" se transmita al siguiente nivel fractal
• NewS = S + f = S + (floor(Mid) - 1) — nuestra nueva "S" para transferir al siguiente nivel fractal

Una característica distintiva de este caso es que no se da una recolección de probabilidades en este bloque, porque esta recolección solo es posible en los valores límite de "U", donde las cadenas de probabilidad también se reflejan en el corredor para que puedan extenderse más. La construcción de un fractal para calcular la probabilidad de cruzamiento con el límite superior será idéntica, con la única diferencia de que la recopilación de probabilidades no se realizará en el primer caso, sino en el segundo.

Una característica interesante de la construcción de estos fractales es la presencia obligatoria de la fórmula de Bernoulli en dichas funciones. Las combinaciones se resaltan en rosa, mientras que los productos de las probabilidades se resaltan en amarillo. Juntos, estos dos factores forman la fórmula de Bernoulli.

Ahora, vamos a comprobar simultáneamente tanto la exactitud de la construcción del fractal completo como el supuesto de que la esperanza matemática del beneficio depende solo de la capacidad predictiva. Los pasos se pueden representar como puntos y como transacciones; en el último caso, los puntos simplemente deberán multiplicarse por el coeficiente de proporcionalidad adecuado, que depende de los lotes y el tamaño del tick, pero, en este caso, veremos qué aspecto tendrá por puntos, porque tal representación es universal:

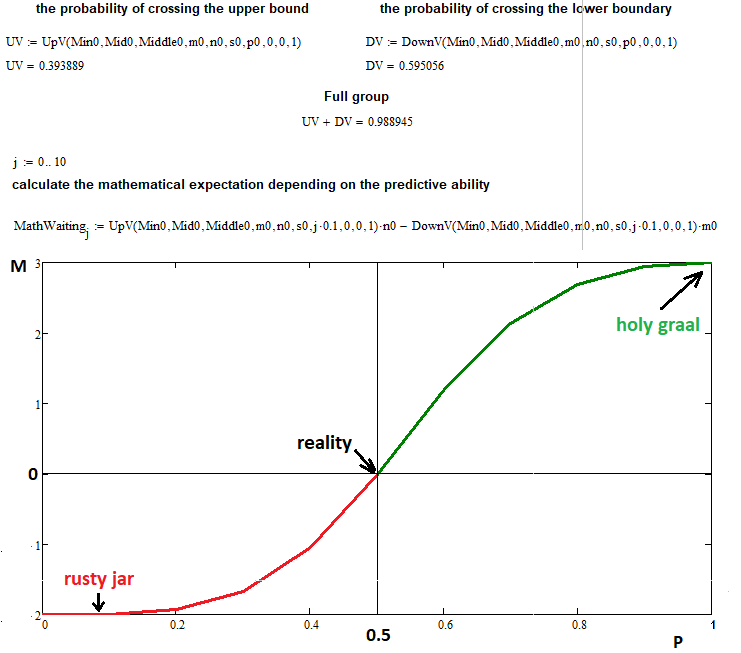
En este ejemplo, hemos tomado los siguientes datos de entrada para dibujar la esperanza matemática respecto a la probabilidad de un paso hacia arriba:

• n = 3 — número de segmentos superiores
• m = 2  — número de segmentos inferiores
• s = 22  — número de pasos permitidos para una reacción en cadena de una función fractal (si la aumentamos, se vuelve muy difícil para la computadora, pero esta cantidad de pasos también basta para lograr una precisión suficiente)
• 0 ... 0.1 ... 0.2 ...... 1.0   — hemos dividido el intervalo de probabilidades de un paso hacia arriba en "10" partes con un salto igual a "0,1"

Como podemos ver, con una probabilidad igual a "0.5", la esperanza matemática de nuestras transacciones es exactamente igual a cero, como predice la fórmula que hemos probado usando este fractal. En los puntos extremos "0" y "1", podemos ver que el valor de la función tiende a "n" y "-m", lo cual es totalmente consistente con nuestras suposiciones. El fractal ha completado con éxito su tarea, aunque ha descubierto un inconveniente completamente predecible: un aumento similar a una avalancha en la complejidad y el tiempo de cálculo. Si surge la necesidad, no creemos que resulte tan difícil esperar una hora o dos, e incluso un día, dado que esta es la única forma de resolver muchos problemas.

También querríamos decir que este fractal funcionará solo para los casos en que "n> = m", en otras palabras, cuando la eliminación del límite superior del punto de partida es mayor que la eliminación del límite inferior, pero, en general, no tenemos que prever dichos casos en el fractal. Esta construcción es inversa en el sentido de que si de repente  "n <m", solo tenemos que calcular este fractal transmitiendo "m" en lugar de "n", y "n" en lugar de "m", y luego también intercambiar las probabilidades, obteniendo una simple mezcla de dos valores: todo esto se hace muy fácilmente. Dichos fractales pueden utilizarse no solo para poner a prueba algunas fórmulas, sino también para invertir el proceso. Algunas fórmulas solo se pueden obtener como resultado de la aplicación de fractales.

Resumiendo

Si estudiamos detenidamente este material, podemos extraer las siguientes conclusiones, muy importantes:

• La teoría de la probabilidad, junto con la programación, puede ofrecernos una base teórica para describir muchos de los procesos del mercado.
• Se ha demostrado que los fractales junto con las principales disposiciones de la teoría de probabilidad pueden ofrecer respuestas a las preguntas más difíciles.
• Hemos analizado por completo un ejemplo de construcción de un fractal bastante complejo.
• Toda la teoría ha sido puesta a prueba en la práctica usando la programación en el entorno MathCad 15.
• Asimismo, hemos demostrado que el esquema de Bernoulli ofrece oportunidades para construir fractales con dos estados de pasos.

Conclusión

Esperamos que el lector haya podido extraer de este material algo nuevo y útil para su propio uso práctico en el comercio. Hemos tratado de transmitir todo el poder de las matemáticas discretas y la teoría de probabilidad para ayudar al lector en la complicada tarea de describir los procesos de mercado usando cadenas de probabilidad fractal. Asimismo, hemos intentado combinar todas las posibilidades principales de la teoría de probabilidad en un monolito que nos ayudará a resolver tareas complejas referentes a la aplicación práctica en el comercio. También hemos tratado de descartar lo información innecesaria que pueda confundir nuestros cerebros. En el próximo artículo, veremos nuevos ejemplos de aplicación práctica de fractales, además de obtener respuestas a otras preguntas igualmente importantes.