取引のための組合せ論と確率論(第I部):基本

内容

• はじめに
• 確率論が市場分析に役立つ方法
• 手動および自動取引に適用される確率論の詳細
• 確率の木と仮説
• フラクタルについて
• ベルヌーイスキーム
• 初めてのフラクタル作成
• まとめ
• 終わりに

はじめに

私の意見では、確率論の言語は、完全に異なるレベルで市場内で実行されているプロセスの理解を提供することができます。確率論の詳細を理解すると、まったく新しい方法で考え始めることができます。漠然としたアイデアや証明されていないヒントが実際の口座で急いで取引したいという欲求を引き起こすことはなくなります。一方で、この新しいアプローチが快適でない人もいるだろうこともわかります。この連載では、取引に対する実際の正しいアプローチを紹介したいと思います。すべての決定は数字のみに基づくべきであり、「たぶん」、「もしも」、「ようだ」などの想定は避けるべきです。

確率論が市場分析に役立つ方法

私は人生のかなり長い間技術科学に携わってきましたが、確率論は私にとって最も困難でした。その可能性がどれだけ広いのかわからなかったからです。確率論の議論の余地のない利点は、その無限の能力です。これは自分の創意工夫と勤勉さ、そしてもちろん知性にのみ依存します。技術的な研究に何年も費やした後、私は、知性が同じタイプの操作を実行するときのスピードと注意力についてではなく、心の柔軟性についてであることに気づきました。たとえば、微分数学、ベクトル場とスカラー場の理論、さらには基礎的代数について考えると、それらはすべて特定の規則または推奨事項を暗示しており、それに従うことでほとんどすべての問題を解決できます。すべての非標準的なタスクは私たちの脳にとってショックです。確率論では、そのような瞬間は無限にあります。ここでは、まったく異なるアプローチによってのみ多くの問題を解決できます。言い換えれば、知性は与えられた問題を解決するための勤勉さと意欲によってのみ開発することができ、確率論はこれを助けることができます。

確率論の枠組みは、数学的な期待値、さまざまな事象の可能な確率、平均値、パーセンタイルなどの基本的な取引の概念を記述します。確率論は、完璧な取引システムは存在せず、各システムには独自のリスクがあると主張しています。私たちにできることは、リスクがあまり不快感を引き起こさない取引システムを選択することだけです。さらに重要なのは、これらのリスクを正しく解釈することです。言い換えれば、感覚や視覚的近似の不正確な言葉から明確な定量的基準に移行することです。もちろん、視覚的評価も重要ですが、定量的変数と組合せればより効果的に機能します。1つの記事ですべての詳細とニュアンスを説明することは不可能ですが、ここにいくつかの興味深い情報を含めるようにします。ここで読者に何か役立つものが見つかることを願っています。

手動および自動取引に適用される確率論の詳細

市場分析に確率論を使用する前に、まず事象とその確率について理解する必要があります。事象は、いくつかの基準を満たす、またはいくつかの基準に従って特定のセットにグループ化される結果のセットです。結果は、特定のグループ内の他のすべての要素と等しい特定の基本要素です。グループとは、プロセスのすべての可能な結果です。プロセスの種類、その物理学、プロセスにかかる時間はそれほど重要ではありません。重要なことは、このプロセスの結果として、プロセスが完了する前に存在していなかったものを取得することです。私たちの事象に関連するこれらの結果は、本質的に私たちの事象です。便宜上、私たちはそれらを1つのオブジェクトに結合します。上記のアイデアは、次のように視覚化できます。

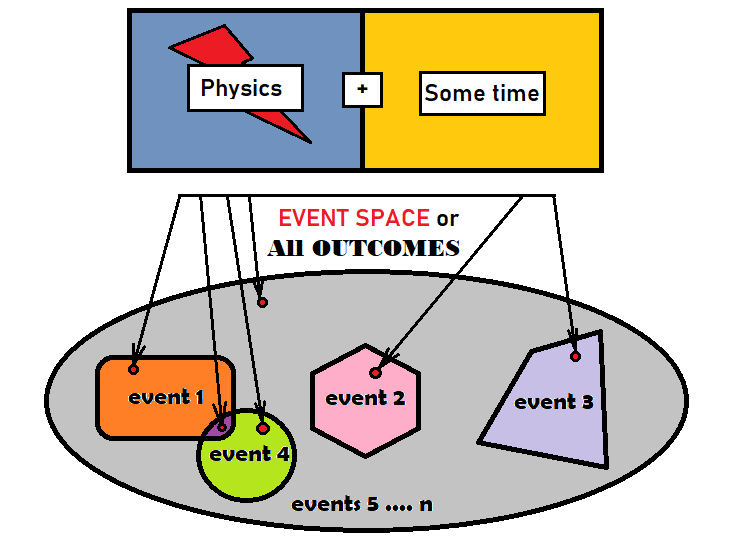
上の図の灰色の楕円は、すべての結果として機能します。数学では、事象空間と呼ばれます。これは、事象空間が幾何学的な形状をしていることを意味するものではありませんが、これらの概念を説明するのに非常に適しています。楕円の中には4つの事象があります。図からわかるように、各事象の中に小さな赤い点があります。このような点の数には、検討中のプロセスによって、制限がある場合とない場合があります。図では2つの事象が交差しています。このような事象は、重複すると言われます。両方の事象に属する結果がいくつかあるということです。他のすべての事象は、楕円のさまざまな部分に配置され、幾何学的に交差しないため、非重複です。灰色の領域の残りの部分は余事象と見なすことができます。または、灰色の領域がなくなるまで小さな部分に分割することもできます。

各事象には、通常確率と呼ばれる対応する数字が少なくとも1つあります。確率とは、同じ実験を無限に行うことができた場合に、同じプロセスの繰り返し中にこの事象が発生する頻度を意味します。事象空間には次の2種類があります。

1. 可能な結果の数が有限
2. 可能な結果の数が無限

結果の数が有限である場合、確率は次のように計算できます。

• P = S/N、ここで、Sは事象基準を満たす結果の数、Nは事象空間内のすべての結果の総数です

場合によっては、特定の空間での結果の数が無限である場合、この確率は、たとえば積分を使用して決定することもできます。上の画像の場合、値「S」と「N」は、それらの幾何学的形状の領域に置き換えることができます。

事象空間が何であるかを明確に定義したり、結果の数や事象によって記述された物理学を定義したりすることが常に可能であるとは限りません。これらのグラフィカルな表現は、脳がデータを類推するのに役立つはずです。これにより、一部のジオメトリを操作せずに、何が起こっているのかを理解しようとする代わりに、確率とこれらの確率に対応する追加の数値のみを操作するという考えに脳が慣れることができます。 事象は、状態と呼ばれることもあります。状態の論理を使用する場合、確率は、同じ実験を繰り返した結果として特定の状態が出現する頻度とまったく同じです。 

図の領域と同様に、楕円に含まれるすべての図の領域の合計は、この楕円の領域と正確に等しくなります。数学の観点から、領域はそこに分類される結果の数です。したがって:

• N = S[1] + S[2] + ... + S[n]
  
• Sは、特定の事象の結果の数です
• Nは事象空間のすべての結果です

等式の両側を値Nで除算することにより、確率論全体の根底にある、興味深く非常に重要な関係が得られます。

• 1 = S[1]/N   +   S[2]/N   +   ...   +S[n]/N

この比率は、非重複事象に対してのみ機能します。事象が結合されると、形状領域が重なり、それらの領域の合計が元の楕円の領域よりも大きくなるためです。これはパズルに似ており、すべてのパズルのピースの領域が結果の画像と正確に等しくなります。この場合、パズルのピースは事象の1つを表しています。これらの分数はすべて、特定の事象の確率を表しています。

• 1  = P[1]   +   P[2]   +   ...   +P[n]

この比率は、排反事象集合という用語の基礎として機能します。排反事象集合は、事象の特定の空間を形成する、すべての非重複事象の統合です。パズルの場合、排反事象集合はすべてのパズルのピースです。これらすべての事象の合計確率は1に等しくなければなりません。つまり、これらの事象の1つは、実験の結果として必ず発生する必要があります。どの事象が発生するかはわかりませんが、実験の結果からわかります。

上記によると、選択した事象空間からの結果の集合は、事象として機能できます。これは、排反事象集合をすべての可能な方法と組合せで収集できることを意味します。有限数の結果を扱う場合、そのような組合せの数は限られている可能性があります。 結果の数が無限の場合、組合せの数は常に無限になります。結果の数が無限大に等しいことがわかっている場合、数学者は乱数値の概念を検討します。場合によっては、タスクで許可されているため、乱数値の方が操作が便利な場合があります。乱数値は、事象空間を記述するための多少異なる方法です。この場合、結果は1つ以上の数値の明確な集合になります。これはベクトルと言えます。この検討モデルは、確率密度の概念を意味します。 

これらの概念は、このトピックを研究するときにさらに使用されるので、ここで検討してみましょう。確率密度は、事象空間全体を表す関数です。この関数の次元は、この事象空間の各結果を説明するために必要な数と正確に同じです。たとえば、射撃場で的を狙う問題を考えると、的が平面(2次元)であるため、この関数の次元は2になります。この場合、特定の結果はX座標とY座標によって特徴付けられます。これらの数値は確率変数であるため、次のように書くことができます。

• R = R(X,Y)
• Rは、座標(X、Y)の点に弾丸が当たる確率密度です

この関数の特性は、この関数のすべての変数の負から正の無限大までの完全な積分が1に等しくなるようになっています。これは、上記の方程式を証明します。ここでの確率は、関数が提示されている領域の積分によってのみ決定されます。さまざまな事象は、区分的に統合された領域で構成できます。したがって、事象の数は無限であるため、必要な数の事象を記述することができます。この記事の枠組み内では、この定義で十分です。

重複事象についてもう少し詳しく説明したいと思います。このような事象は、全体像を一般的に理解するためにも非常に重要です。非重複事象の処理は重複事象と比較して簡単になるはずです。確率論では、事象の組合せまたは分割を処理する必要がある場合があります。ただし、ここで関心があるのは、これらの変換の結果として表示される確率にのみです。この目的のために、事象の和と積の概念、および逆関数法を使用します。これらの操作は、数学と同じ意味ではありません。さらに、それらは確率でのみ動作します。結合された事象の確率は、集合の整合性に違反するため、追加できません。一般に、ソース事象に適用されるこれらの3つの操作は、ソース事象の断片から構成できるすべての可能な事象を記述できます。2つの重複事象の例を使用して、平面上でどのように見えるかを示すことができます。

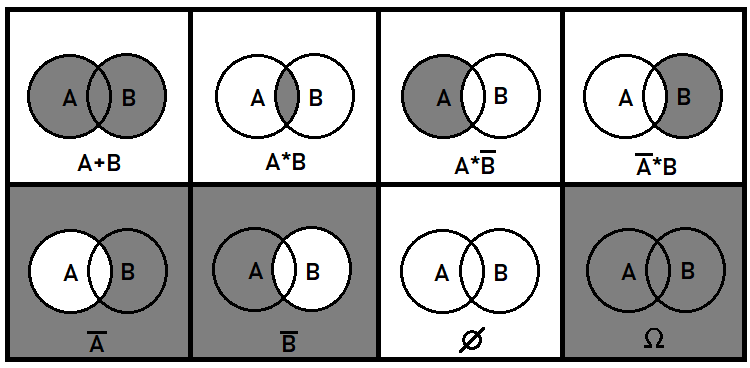
追加の代数演算は、上記の演算で構成できます。たとえば、ブール除算は、選択した事象の逆数を乗算することと同等であるため、上の図の3番目と4番目の状況と同等です。厳密に言えば、最初の2つの事象は、ソース事象の一部で構成できるすべての可能な事象を説明するのに十分です。重複する事象が3つ以上ある場合は、はるかに困難です。この記事では、重複しない事象のみを扱います。

市場の数学は、主にランダムウォークの概念に基づいています。この概念を検討し、パターンの存在によってこれらの事象を一般化することが可能になります。始値から等間隔にあるストップロスとテイクプロフィットでポジションを開くと仮定します。ここでは、スプレッド、手数料、スワップは考慮していません。したがって、無料でポジションを開き、さまざまな方向とさまざまなチャートポイントでランダムに取引する場合、利益と損失の比率は1に等しくなります。言い換えれば、収益性の高いポジションの数は、無限の取引での負けポジションの数に等しくなります。以上のように、どれだけ長く取引しても利益はゼロになります。すべての手数料、スプレッド、スワップを適用すると、最終的な結果はマイナスになります。

このプロセスの数学は常に損失につながるため、ランダムウォークは無意味に見えるかもしれません。ただし、ランダムウォークは、さまざまな事象の確率を計算するのに役立ちます。これらには、非対称ストップによる終値、またはチャートが特定の価格範囲で通過する平均価格が含まれる場合があります。また、リスクの計算や、利益の最大化や損失の最小化の試みに役立つ、ポジションの存続期間やその他の有用な変数を計算することもできます。

確率の木と仮説

前頭葉を発達させるための非常に有用な例は、事象の木または確率の木です。このトピックは、すべての確率の木の基礎となるベルヌーイスキームに由来します。このスキームは、互いに続く非重複事象の連鎖を調べます。ただし、その前に、全確率の公式について考えてみましょう。この重要な構造を研究することにより、ベルヌーイスキームに進み、確率の木に進むことができます。式は次のようになります。

• P(A) = Sum(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] - 事象Aの確率
• P(H[i]) — 仮説の確率H[i]
  
• P(A|H[i]) — 仮説H[i]の枠組み内で事象Aが発生する確率

確率を扱うときは、仮説のスタイルで書く方がよいと言いたいです。たとえば、エントリP(H[k]|H[i])は次のことを意味します。

1. 空間H[i]に対して計算された事象H[k]の確率

このようにして、どの事象が空間と見なされ、どの事象がネストされているかが明確になります。実際のところ、各事象は小さな事象空間であり、その中に他の事象が存在する可能性があり、事象空間としても機能する可能性があります。このロジックによれば、エントリP(H[i])は次のように記述できます。

• P(H[i]|O) — この確率はOに対して推定されるためです。
  

それでは、全確率の公式をいくつかの部分に分割して、その背後にあるものを理解しましょう。一見難しいように見えるかもしれませんので、わかりやすくしましょう。まず、式を少し異なる形式で書き直します。

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — 仮説H[i]の交点の特定のセグメントの領域
• N[i] — 仮説全体の領域H[i](S[i]を含む)
• O —すべての結果または楕円全体の領域

分子と分母に値N[i]を乗算することで構成された小さな変換の後、元の式に存在する確率を確認できます。

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

次のようにグラフィカルに視覚化できます。

 

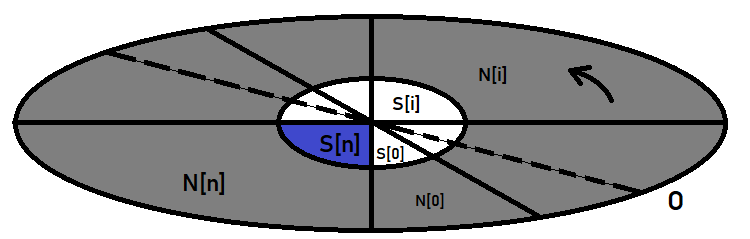
外側の楕円は事象空間です。中央の楕円は私たちの事象であり、私たちが探している確率です。時計だとします。楕円の直径を描き、反時計回りに回転させ、楕円を仮説であるセグメントにカットします。仮説は、事象の特別な名前にすぎません。ただし、実際には同じ事象であり、確率を計算している事象と同じです。

この式には、ベルヌーイスキームの構築に役立つ特殊なケースがあります。中央の楕円が完全にこれらの仮説の1つに含まれていると想像してください。次に、これらの仮説内で事象Aが発生する確率は不可能であるかゼロに等しいため、残りの仮説に関連するこの合計のすべての項が自動的にゼロになり、最終的にこれらの項がゼロになります。その結果、次のことがわかります。

• P(A) = P(H) * P(A|H)
• H —選択された事象が完全に配置されている仮説の確率。

さらに、事象Aが仮説とも呼ばれると仮定するとどうなるでしょうか。これは可能です。仮説は事象であるため、どの事象も仮説です。ここで、Aの内部に別の事象Bがあるとします。その場合、AはBに関連する仮説であり、前の式はこれら2つの事象に適用できます。

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

P(A)の代わりに前の比率を挿入します。任意の数のネストされた仮説または事象の一般式を作成する際に特定のパターンを確認できます。それの目的は何ですか？これは少し後で検討するベルヌーイの定理の直接のプロトタイプです。ここで、考慮すべきもう1つの興味深い事実があります。

フラクタルについて

上記の式によると、P(A)+ P(B)= 1の場合、これは排反事象集合です。これは、完全なグループが、互いにネストされた2つの任意の仮説連鎖で構成できることを意味します。しかし、これらの仮説は重複している可能性があります。ネストされた可能性のあるすべての仮説が他の連鎖の仮説と重複しないようにする必要がある場合、自動的にすべての連鎖がこの事象空間内のすべての連鎖と重複しなくなります。そのグラフィカルに表示は非常に興味深いパターンを示します。

このパターンはフラクタルと呼ばれます。これは、このような構造は無期限に構築できるので、最後まで構築することができないためです。上の図では、構造の深さはわずか3レベルです。青い長方形は、確率の別の連鎖の終わりを表しています。これらすべての連鎖の確率を合計したものは排反事象集合を形成します。

このようなフラクタルは、組合せでよく説明できます。組合せは階乗の概念に基づいています。別の概念として順列があります。これは、階乗と組合せの間のどこかにあります。順列式は階乗式から導出され、組合せの概念は順列式から導出されます。対応する式は次のとおりです。

• n!- 数nの階乗
• P(n,k) = n!/ ( n - k )!  — N個の要素からのK個の要素による順列
• С(n,k) = n!/ ( k!* ( n - k )! )  — N要素とK要素の組合せ

階乗は、1で始まりnで終わるすべての自然数の積であり、0!= 1です。つまり、ゼロの階乗は1に等しくなります。この場合、これはルールの単なる例外ですが、この例外が計算を妨害したり、アルゴリズムを複雑にしたりするケースは1つもありません。

順列はもう少し複雑です。あなたがカードのデッキを持っていて、このデッキに特定の数のカードがあると想像してください。簡単な実験を行います。デッキをシャッフルします。完全に任意の方法でデッキからカートをいくつか取り出し、取り出された順序でテーブルに置きます。したがって、順列は、この実験で考えられるすべての結果の数ですが、カードの順序も特定の結果の一意の識別子と見なされます。このような順列は、任意の要素に適用できます。

最初のカードはn種類の方法でデッキから取り出すことができ、2番目のカードは「n-1」の方法で取り出すことができます。これは、最初のカードがデッキにないためです。これが、カード「n-k-1」まで続きます。可能なすべての順列の数を取得するには、「n-k-1」から「n」までのすべての数を乗算する必要があります。この手順は階乗に似ています。「n!」を「n-k」係数で割ると、「(n-k)!」と正確に等しい元の積が得られます。これが順列式を取得する方法です。

組合せ式はもう少し複雑ですが、推測するのも非常に簡単です。考えられるすべての順列がありますが、要素の順序は重要ではありません。このセットのカードだけが重要です。ここで、そのようなケースの数を見つける必要があります。各ケースには異なるカードのセットがあります。実際、各順列にはすでにこれらの一意のセットの1つが含まれていますが、すべてが必要なわけではありません。ロジックを変更して、考えられるすべての組合せのすべての順列を収集してみましょう。組合せを取得すると、その中の要素をどのように再配置しても、それらは一意になることがわかります。さらに、すべての一意の組合せを取得し、それらの内部で可能なすべての順列を生成すると、次のようになります。

• P(n,k) = C(n,k) * P(k,k)

「k」バリアントからこれらの「k」バリアントのすべての可能な順列を収集する必要があるため、組合せ内のすべての可能な一意の順列の数は「P(k,k)」に等しくなります。方程式の両方の部分を「P(k,k)」で割ると、必要な組合せの式が得られます。

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

順列と組合せの両方が、さまざまな確率論の問題に広く使用されています。実際の応用に関して言えば、私たちにとって非常に役立つのは組合せです。組合せは、さまざまな目的でフラクタル関数の構築に使用されます。おそらくそれらを再帰と呼ぶ方が正しいでしょうが、何らかの理由で私はそのような関数をフラクタルと呼びます(おそらくそれらは本当にフラクタルであるため、再帰だけでなく呼び出しの木全体です)。

ベルヌーイスキーム

このようなフラクタル関数の研究に進む前に、よく知られているベルヌーイの公式について考えてみましょう。数回繰り返す必要のある一連の同一の実験があるとします。実験の結果、一定の確率で事象が出現または非出現するはずです。さらに、一連の「n」回の実験で、事象が正確に「k」回出現する確率を見つけたいとします。ベルヌーイの定理はこの質問に答えることができます:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)   — ベルヌーイの定理
  
• p — 1回の実験の結果として事象が発生する確率
• q = 1-p — 実験の結果として事象が発生しない確率

確率的連鎖について以前に導出された式を覚えていますか。それを、任意の大きな連鎖長に拡張してみましょう。

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n — 連鎖内のセグメントの数
• O — 一連の結果全体。 H[0]として表すことができます

この式は、正確に必要な一連の仮説が発生する確率を計算します。式は次のように視覚的に表すことができます。

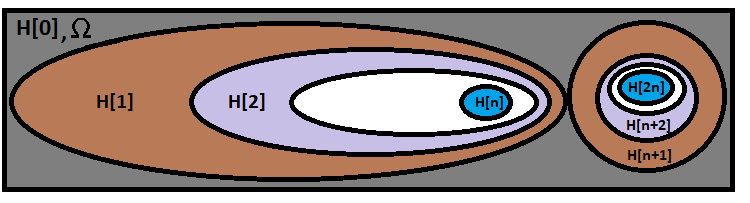
私たちの数式は最初の最大の楕円にありますが、右側の別の連鎖は連鎖と重複しておらず、別の組合せからの他の分岐を象徴しています。数式の組合せを計算するためのバリアントとまったく同じ数の分岐があります。組合せを組合せ計算バリアントと混同しないでください。組合せを計算するためのバリアントの数は次のとおりです。

• n+1(「0」の成功した結果の組合せもカウントされるため)
• nは、一連の実験における独立したテストの数です

ここで、これらすべての仮説の確率が「p」または「q」のいずれかに等しいと想像してください。次に、式が簡略化されます。

• P(n) = Pow(p,k)*Pow(q,n-k)
• k — 積にある「p」に等しい因子の数
• n-k — 積にある「q」に等しい因子の数

それはすでにベルヌーイの定理に似ていますが、組合せが欠けています。注意深く考えると、同様の確率と「k」と「n-k」の量を持つ連鎖のバリアントは「C(n,k)」と正確に等しいことが明らかになります。確率のすべての連鎖は重複していないため、これらの連鎖の1つを取得する確率は、そのようなすべての連鎖の確率の合計です。これらの確率はすべて同じであるため、1つの連鎖の確率にそれらの数を掛けて、ベルヌーイの公式を得ることができます。

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

この式は、たとえば、厳密に固定された組合せではなく、k回以上、k回以下、およびすべての同様の組合せで発生する事象の確率を見つける必要がある場合に、さらに拡張できます。この場合、必要なすべての組合せの確率の合計になります。たとえば、事象がk回を超えて発生する確率は、次のように計算されます。

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

次を理解することが重要です。

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

言い換えると、考えられるすべての連鎖が排反事象集合を形成します。もう1つの重要な方程式は次のとおりです。

• Summ(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

確率連鎖の各セグメントには、「事象が発生」と「事象が未発生」の2つの状態しかないことを考えると、論理的です。事象が発生しなかった状態も、別の事象が発生したことを意味する事象です。

組合せには、もう1つの興味深い特性があります。

• C(n,k) =  C(n,n-k)
  

これは次のように導き出されます。「C(n,n-k)」を計算し、「C(n,k)」と比較します。小規模な変換の後、両方の式が同一であることがわかります。上記のすべてのステートメントをチェックするために、MathCad15に基づいた小さなプログラムを作成しました。

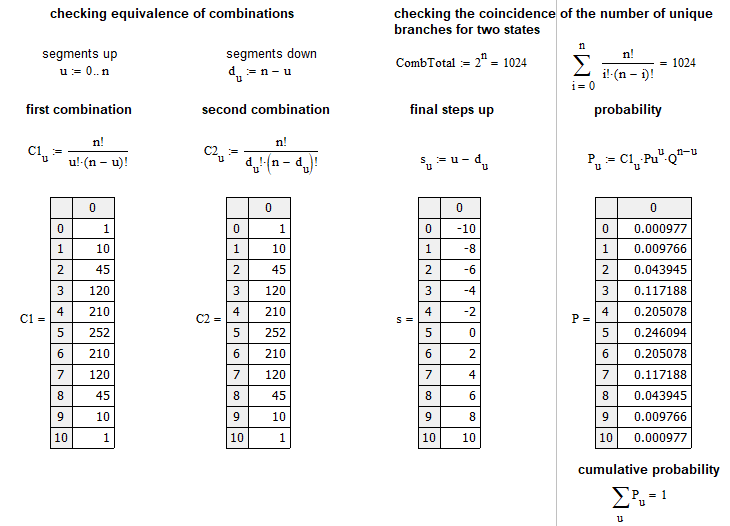
この例は市場に近いです。nステップのうち、市場がuステップ上に移動する確率を計算します。ステップは、前のステップと比較して、特定のポイント数だけ上下する価格の動きです。各「u」の確率の配列は、次のようにグラフィカルに表示できます。

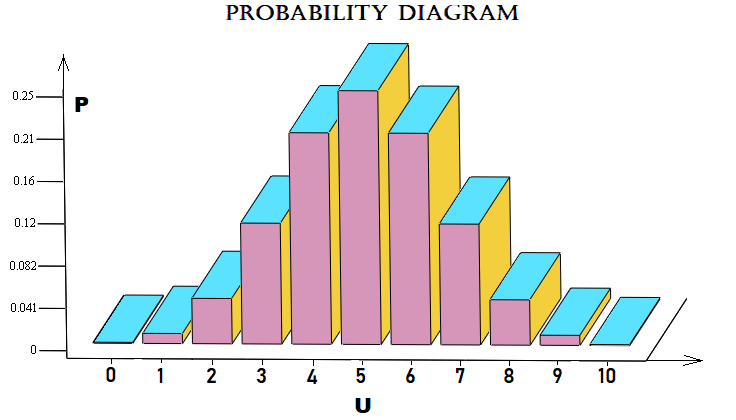
簡易化のために、10ステップのベルヌーイスキームを使用しました。ファイルは以下に添付されているので、テストすることができます。このスキームを価格設定に適用する必要は必ずしもありません。注文などにも適用できます。

初めてのフラクタル作成

ストップロスとテイクプロフィットレベルに関連する問題には特別な注意を払う必要があります。ストップロスとテイクプロフィットの値がポイント単位(現在の価格からの距離)でわかっている場合、ストップロスまたはテイクプロフィットによって取引が成立する確率を何らかの方法で計算する必要があります。これらのすべての側面は価格設定メカニズムに直接依存しているため、これが始値でなくなった場合でも、この値はいつでも計算できます。この例では、フラクタルを使用して式の証明を示したいと思います。ランダムウォークの場合、この確率は次のように計算できます。

• P(TP) = SL / ( TP + SL ) - テイクプロフィットに達する確率
• P(SL) = TP / ( TP + SL ) - ストップロスに達する確率
• SL — ストップロスへのポイント距離
  
• TP — テイクプロフィットへのポイント距離

これらの2つの確率は、排反事象集合を形成します。

• P(TP) + P(SL) = 1
  

この公式によれば、ランダム取引の場合、スプレッド、手数料、スワップを除外すると、そのようなストラテジーの数学的な期待値はゼロになります。

• M =  P(TP) * TP - P(SL) * SL = 0

これは、固定のストップレベルを設定した場合の最も単純なケースです。しかし、それを絶対にどんなストラテジーにも一般化することは可能です。それでは、同じMathCad15を使用して式を証明しましょう。私はこのプログラムを長い間使用してきました。プログラミングを使用していても、ほぼすべての複雑さのレベルの計算を生成できます。この例では、上記の式を証明することに加えて、フラクタル式を作成する最初の例を示します。価格変動プロセスをスケッチすることから始めましょう。ここでは連続関数を使用できず、離散関数のみを使用できます。このために、条件付きの注文を取り、ストップレベルの距離を上下に計算してから、これらのセグメントを等しいステップの部分に分割して、各ステップに整数のステップが含まれるようにします。価格がこれらのステップで移動することを想像してみてください。ステップが等しいため、2つの方向のいずれかでステップが発生する確率は0.5です。適切なフラクタルを実装するには、グラフィカルな表現が必要です。

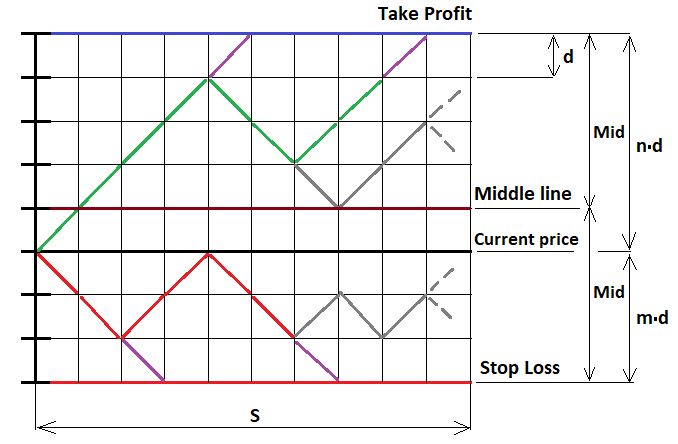
この問題を解決するために、考えられる3つのフラクタル継続のケースを考えてみましょう。

1. 中央線より上(U> MiddleLine)
2. 中央線より下(U <MiddleLine)
3. 中央線のレベル(U = MiddleLine)

「U」は、始値に対する「u-d」の合計ステップ数です。フラクタルを構築し続けるポイントが価格を下回っている場合、Uは関数に従って負の値を取ります。中央線にある場合、線を越えることを恐れずに実行できるステップ数は、中央線より1つ少なくなります。ただし、構築を進める前に、フラクタルの構築を価格または注文で実行できるステップ数に制限する必要があります。ステップ数が必要な数を超える場合は、それ以上の構築を中断する必要があります。そうしないと、無限の再帰が発生し、抜け出すことができなくなります。その計算時間は無限大に等しくなります。

この図では、いくつかの紫色のステップを描画しました。これらのポイントで、確率を収集し、それらを共通の変数に合計します。その後、連鎖が接触した境界に応じて連鎖を上下に回転させ、連鎖がさらに移動して新しいネストされたフラクタルレベルを構築できるようにする必要があります。その他の点では、ベルヌーイスキームに基づいて完全なフラクタルレベルを自由に構築できます。

ベルヌーイスキームに基づいて木を作成できる場合は、最初に、すべてのステップが上のみまたは下のみの場合の極端なケースを考慮して、実行できるステップ数を決定する必要があります。3つのケースすべてで、値は次のようになります。

• (n - 1) - U  — 連鎖がすでに中央線より上にある場合(Uが増加すると、上限までの距離が減少するため)
• (m - 1) + U  — 連鎖がすでに中央線より下にある場合(Uが減少すると、下限までの距離が減少するため)
• (floor(Mid)-1)  — 連鎖がちょうど中央線にあるとき
• n — 上位セグメントの数
• m — 下位セグメントの数
• floor  — この関数は小数部分を破棄します(これは必要ない場合があります)

まず、2つの補助値を計算する必要があります。

• Mid =(m + n)/ 2 — 範囲幅の半分(ステップ単位)
• Middle = (m+n)/2 - m — 中央線の「U」値(ステップ単位)

これらの値は、後でフラクタル分岐ロジックを説明するために使用されます。今のところ、「n> = m」の場合のみフラクタルを作成します。ただし、このデータはフラクタルを構築するのに十分ではありません。より深いフラクタルレベルを構築できるようにするには、ベルヌーイスキームからの新しい組合せごとに「U」を再定義し、それを新しいフラクタルレベルに渡す必要があります。さらに、実行されるステップの数を正しくインクリメントし、さらにそれらを正しく渡す必要があります。同様に、次のフラクタルレベルの乗数を使用して連鎖全体の確率を収集し、このプロセスが必要な境界を正常に通過して終了するまで、中間連鎖の確率をさらに次のレベルに渡す必要があります。次の画像は、これら3つのバリアントを説明しています。

  

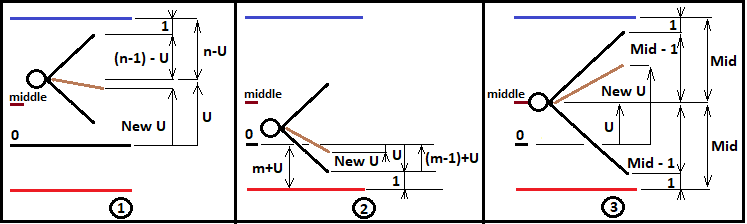
この図に従って、提示された各ケースの値「NewU」およびその他の補助値がどのようになるかを記述できます。上限を超える確率を計算するためにフラクタルを作成する例を考えてみましょう。

ケース1:

上の写真を見て、そこで何が起こっているのかを数学的に説明しましょう。この図は、MathCad15の私のプログラムからの要約を示しています。プログラムのコード全体を以下に添付します。ここでは、フラクタルの基礎となる最も重要な詳細を提供します。最初の長方形はループ内にあり、「i」で繰り返されて、考えられるすべての組合せを記述します。このロジックは、MetaEditor IDEで繰り返すことができます。最初の図から始めましょう。「NewU」を定義するには、最初にいくつかの基本的な式を定義する必要があります。

• ( n - 1 ) - U = f — 将来の組合せツリーのステップ数(距離はフラクタル範囲の最も近い境界までの距離によって決定)
• u + d = f  — 同じ値ですが、上昇セグメントと下降セグメントの数で表されます
• s = u - d  — 下降セグメントと上昇セグメントで表される最終ステップの数
• u = i  — これは、私のプログラムが「i」による反復を使用しているためです(覚えておいてください)

必要なすべての値を計算するには、「s」から「U」および「i」を表す必要があります。このために、変数「d」を除外する必要があります。まずdを表現し、次に「s」の表現に置き換えます。

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

次に、見つかった「s」を使用して、「NewU」と次のフラクタルレベルに渡されるすべての値を見つけます。

• NewU = s + U = -( n - 1 ) + 2*i + 2*U   - 次のフラクタルレベルに渡される新しい「U」
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p,( n - 1 ) - U -i)  — チェーン「P」が次のフラクタルレベルに渡される新しい確率(チェーンの新しいセグメントの確率を乗算することによって得られます)
• NewS = S + f = S + ( n - 1 ) - U  — 次のフラクタルレベルに渡される新しい「S」

次に、下の長方形を見てください。ここでは、ステップチェーンが範囲の上限に達した場合を処理します。次の2つのケースを処理する必要があります。

1. 境界線と交差する連鎖の確率を収集する(赤い下線)
2. 同様のアクション、新しい値をインクリメントして次のフラクタルレベルに渡す

考えられるバリアントは2つしかないため、このケースは非常に単純です。

1. 境界線に触れる
2. 境界線からの反転

これらのアクションは、各ケースが1つのステップのみを意味するため、ベルヌーイスキームを必要としません。交差の確率は「p」であるため、反転の確率はさらに「(1-p)」で乗算されます。前の計算から明らかなように、これら2つのイベントは排反事象集合を形成する必要があります。これは下降する反射であるため、ステップは1ずつ増加し、「U」は「1」減少します。これで、このケースを正しく作成するためのすべてが揃いました。これらのルールは、完全に異なるケースに必要なメインフラクタルを構築するために同一になります。

ケース2:

この場合の計算はほぼ同じです。唯一の違いは、「f」の値が異なることです。

• ( m - 1 ) + U = f

ここでも、前の場合と同じ式を使用して、「s」から「U」および「i」を表現します。

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

同様に、次のフラクタルレベルに渡す必要がある他のすべての値を見つけます。

• NewU = s + U = -( m - 1 ) + 2*i  - 次のフラクタルレベルに渡される新しい「U」
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i)  — 次のフラクタルレベルに渡される新しい連鎖「P」
• NewS = S + f = S + ( m - 1 ) + U  — 次のフラクタルレベルに渡される新しい「S」

下の長方形は、反射が上がるために「U」が1増えることを除いて、前のケースとほぼ同じです。したがって、「U」が増えます。この場合、このフラクタルの下側の境界との交点には関心がないため、確率は収集されません。さて、これが範囲の中央線で連鎖が発生した最後のケースです。

ケース3:

「f」を定義します。

• floor(Mid) - 1 = f

「s」を見つけます。

1. d = f - i =  floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

最後に、次のフラクタルレベルに渡される値を見つけます。

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i)  — 次のフラクタルレベルに渡される新しい連鎖「P」
• NewS = S + f = S + (floor(Mid) - 1) — 次のフラクタルレベルに渡される新しい「S」

このケースの特徴は、ブロックが確率を収集しないことです。これは、確率が「U」の境界値でのみ収集できるためです。確率連鎖も連鎖に反映され、さらに広がることができます。上部の境界を越える確率を計算するためのフラクタルの作成は同じですが、確率は1番目ではなく2番目のケースとしてカウントされます。

そのようなフラクタルがそのような関数にベルヌーイの公式が必須である場合の構造の興味深い特徴です。組合せはピンクで強調表示され、確率の積は黄色で表示されています。これらの2つの乗数は、一緒にベルヌーイの公式を形成します。

ここで、フラクタル全体の構築の正確さと、期待されるペイオフが予測能力にのみ依存するという仮定の2つのことを同時に確認します。手順は、ポイントおよび取引として提示できます。後者の場合、ポイントは、ロットとティックサイズに依存する適切な比例係数で乗算する必要があります。ここではポイントを使用します。この表現は普遍的です。

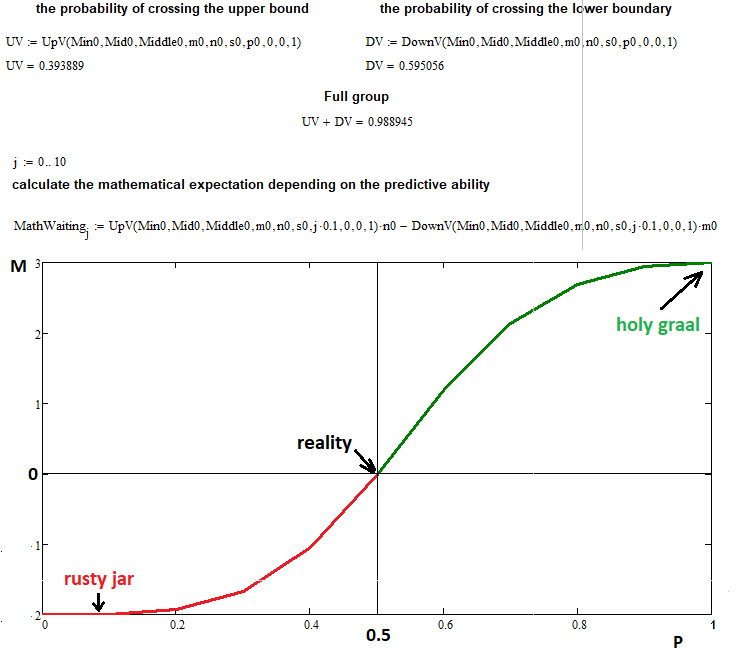
この例では、次の入力データを使用して、数学的な期待値とステップアップの確率をプロットしました。

• n = 3 — 上位セグメントの数
• m = 2 — 下位セグメントの数
• s = 22 — フラクタル関数の連鎖反応の許容ステップ数(この値を増やすと、コンピューターに余分な負荷がかかるため、このステップ数で十分です)
• 0 ... 0.1 ... 0.2 ...... 1.0 — アップステップ確率の範囲を0.1のステップで10の部分に分割

ご覧のとおり、確率0.5の場合、式で以前に予測されたように、取引の数学的な期待値はゼロに等しくなります。極値0および1では、関数値は「n」および「-m」になる傾向があり、これは私たちの仮定を裏付けています。フラクタルはタスクを正常に完了しましたが、計算時間と複雑さが大幅に増加するという欠点が明らかになりました。ただし、同様のタスクを数時間または1日待つことはまったく問題ありません。

このフラクタルは、n> = mの場合、つまり上境界までの距離が下境界までの距離よりも大きい場合にのみ機能しますが、フラクタルでこれを指定する必要はありません。この構造はミラーリングできます。 n < mの場合、nの代わりにmを渡し、mの代わりにnを渡すことで、フラクタルを計算できます。次に、確率を切り替えて、目的の結果を取得します。このようなフラクタルは、数式を証明するためだけでなく、逆のプロセスにも使用できます。一部の数式は、フラクタルを使用した結果としてのみ取得できます。

まとめ

この記事では、次の非常に重要な結論が出されたと思います。

• プログラミングと組合せた確率論は、市場プロセスの多くを説明するための理論的基礎を提供することができます。
• 確率論の主な規定と組合せたフラクタルは、最も難しい質問に答えることができます。
• かなり複雑なフラクタルを作成する例を見てきました。
• 理論全体は、MathCad15環境でプログラミングを使用して実際にテストされました。
• この記事は、ベルヌーイスキームが2つのステップ状態を持つフラクタルを作成する機会を提供することを証明しています。

終わりに

読者がこの資料に新しい何かを見つけて、実際に取引に使用できることを願っています。この記事に取り組んでいる間、フラクタル確率連鎖を使用して市場プロセスを説明するという別の難しいタスクに備えるために、離散数学と確率論の完全な力を伝えようとしました。確率論のすべての主要な規定を1つの資料にまとめようとしました。これは、実際の取引の複雑なタスクを解決するのにさらに役立ちます。また、関係のない詳細はすべて削除することを試みました。次の記事では、フラクタルの実用化の新しい例と他の重要な質問への回答を提供します。