Combinatória e teoria da probabilidade para negociação (Parte I): fundamentos

Sumário

• Introdução
• Por que vale a pena conhecer a teoria da probabilidade ao analisar o mercado?
• Nuances da teoria da probabilidade aplicada para negociação manual e automatizada
• Árvores de probabilidade e hipóteses
• Fractais
• Esquema de Bernoulli
• Criando o primeiro fractal
• Conclusões
• Conclusão

Introdução

Eu estou convencido de que a linguagem da teoria da probabilidade, como nenhuma outra, é capaz de revelar ao trader um nível completamente diferente de compreensão dos processos que ocorrem dentro do mercado. Após dominar as nuances dessa teoria, você começará, antes de tudo, a pensar em outro nível mais elevado. Ao que parece, desse modo, você já não vai tomar decisões apressadas ou ceder ao arroubo de operar numa conta real. Por outro lado, entendo que para muitos essa abordagem é estranha, principalmente porque muitos vivem dentro de um paradigma completamente diferente que lhes proporciona conforto. Quero fazê-lo entrar em razão um pouco e lhe mostrar uma abordagem real e correta de negociação. No topo de tudo deverá haver apenas números e nenhum "talvez", "se" e "acho que".

Por que vale a pena conhecer a teoria da probabilidade ao analisar o mercado?

Vale a pena admitir que durante grande parte da minha vida estive intimamente envolvido na engenharia, e a teoria da probabilidade era a coisa mais difícil para mim. A razão era que eu não entendia quão amplas eram suas possibilidades. Uma vantagem indiscutível é a amplitude ilimitada de suas capacidades que depende apenas de nossa facilidade de compreensão, esforço e intelecto. Quero ressaltar que depois de anos estudando, percebi que inteligência não consiste no quão velozmente realizarmos o mesmo tipo de tarefa ou no quão atentos nos mantemos, ela só revela o quão flexível é nossa mente. Se tomarmos, por exemplo, a matemática diferencial, a teoria dos campos vetoriais e escalares e até mesmo a álgebra da escola, existem em todos os lugares um certo conjunto de regras ou recomendações, a partir das quais podemos resolver quase todos os problemas. Assim que a tarefa começa a ir além do padrão, nosso cérebro fica bloqueado e não entende o que fazer. Na teoria da probabilidade, há um máximo de momentos desse tipo, mas é graças a isso que a solução de muitos problemas só pode ser fornecida por abordagens completamente diferentes. Em outras palavras, a inteligência só pode ser desenvolvida pela dedicação e vontade inesgotável para resolver o problema, e a teoria da probabilidade é para isso.

Dentro do âmbito da teoria da probabilidade, são descritos conceitos fundamentais de negociação, como o valor esperado, as probabilidades de diversos eventos, os diferentes valores médios, bem como percentagens e muito, muito mais. Essa teoria nos ensina que não existe um sistema de negociação perfeito e que cada sistema tem seus próprios riscos. Só podemos escolher o sistema de negociação cujos riscos não nos causarão desconforto. Mas o mais importante é interpretar corretamente esses riscos. Em outras palavras, nós nos afastamos da linguagem imprecisa das sensações ou aproximações visuais para nos acercarmos de critérios quantitativos claros. É claro que os recursos visuais também são necessários, mas funcionam melhor em conjunto com indicadores quantitativos. É impossível descrever todas as nuances num artigo, mas vou mostrar algo interessante aqui. Tenho certeza de que mesmo aqueles que não estão familiarizados com a matemática encontrarão algo para si próprios.

Nuances da teoria da probabilidade aplicada para negociação manual e automatizada

Para usar corretamente a teoria da probabilidade para a análise de mercado, primeiro precisamos nos familiarizarmos com os eventos e suas probabilidades. Um evento é um conjunto de resultados que quer satisfazem a uns critérios quer são agrupados de acordo com um critério num conjunto isolado. Um resultado é certo elemento base que é igual a todos os outros num determinado grupo. O grupo se refere a todos os possíveis resultados de um processo. Não é tão importante que tipo de processo é, qual é sua física ou quanto tempo dura, o mais relevante é que com o fluxo completo do processo vamos obter um resultado ou algo que não existia antes dele ter sido concluído. Esses resultados que se relacionam com o nosso evento, na verdade, são o nosso evento, nós apenas, por uma questão de percepção, os combinamos num único objeto. Podemos descrever convencionalmente o que foi dito na figura:

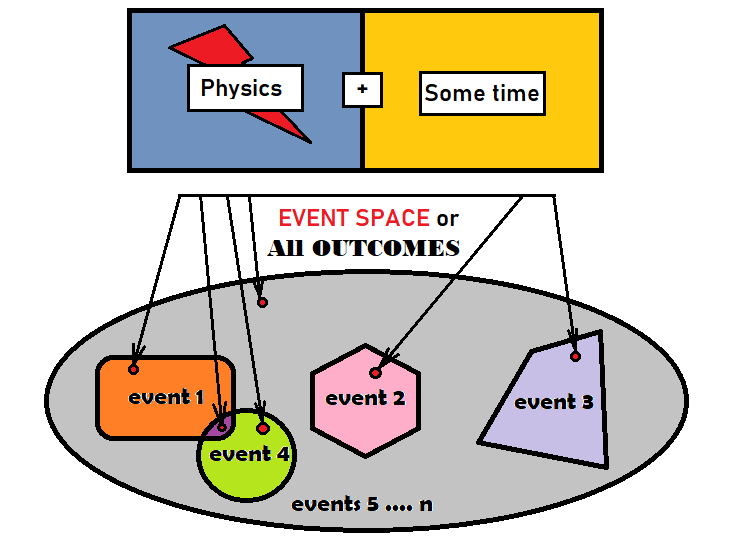
A elipse cinza aqui desempenha o papel de todos os resultados e em matemática é geralmente chamada de "espaço para eventos". Isso não significa que tal espaço tenha uma forma geométrica, ele é só um plano que facilita a descrição desses conceitos. Apresentei 4 eventos diferentes dentro da elipse. Como se pode ver na figura, há um pequeno ponto vermelho dentro de cada evento. Na verdade, esses pontos podem ser um número limitado ou infinito, tudo depende de qual processo estamos considerando. Também na figura existem dois eventos que se cruzam. Esses eventos são chamados de "conjuntos". Eles são chamados assim porque existem resultados que pertencem a ambos os eventos. Os outros eventos são "exclusivos" porque eles estão localizados em diferentes partes da elipse e não se cruzam geometricamente. O restante da área cinza pode ser considerado o último evento ou também pode ser dividido em partes menores até que não haja mais áreas cinza.

Cada evento deve ter pelo menos um número correspondente, que geralmente é chamado de "probabilidade". Probabilidade indica a frequência com que um evento selecionado aparece no processo de repetição do mesmo processo, se pudéssemos gerar a mesma experiência indefinidamente. Existem dois tipos de espaço de eventos:

1. Com um número finito de resultados possíveis
2. Com um número infinito de resultados possíveis

No caso de um número finito de resultados possíveis, a probabilidade pode ser calculada da seguinte forma:

• P = S/N , S é o número de resultados que atendem aos critérios do evento; N é o número total de todos os resultados no espaço do eventos

Em alguns casos, quando o número de resultados num determinado espaço de eventos é infinito, também podemos determinar essa probabilidade, por exemplo, usando integrais. Especificamente, no caso da nossa imagem, os valores "S" e "N" podem ser substituídos pela área das suas formas geométricas.

Nem sempre é possível definir claramente o que é o espaço de eventos, assim como nem sempre é possível determinar explicitamente quantos resultados ele contém e que tipo de física eles descrevem. Essas representações gráficas têm como objetivo apenas ajudar a fazer analogias, para que nosso cérebro comece a se acostuma com a ideia de que trabalhamos exclusivamente com probabilidades e números adicionais que correspondem a estas últimas. Mais eventos podem ser chamados de "estados". Se usarmos a lógica dos estados, descobriremos que a probabilidade nada mais é do que a frequência de ocorrência de um determinado estado como resultado da repetição de experimentos idênticos. 

Se continuarmos a lógica das áreas das figuras, veremos que a soma das áreas de todas as figuras incluídas na elipse é exatamente igual à sua área. Se já levamos isso para uma linguagem matemática, então a área é o número de resultados que calham nela. Acontece que:

• N = S[1] + S[2] + ... + S[n]
  
• S - número de resultados de um determinado evento
• N - todos os resultados do espaço de eventos

Se dividirmos os dois lados da igualdade pelo valor "N", obteremos uma relação interessante e muito importante que fundamenta toda a teoria da probabilidade:

• 1 = S[1]/N   +   S[2]/N   +   ...   +S[n]/N

Eu só quero esclarecer que essa proporção funciona apenas para aqueles eventos exclusivos, pois se os eventos forem mútuos, então as áreas das figuras já começam a se sobrepor, e sua área total já será maior que a área da elipse inicial. Todos nós montamos algum quebra-cabeça na infância, então está claro que a área de todas as células do quebra-cabeça é exatamente igual à área da imagem que obtemos no final. Nesse caso, uma peça do quebra-cabeça representa um dos eventos. Continuando, está claro que todas essas frações nada mais são do que as probabilidades de eventos específicos:

• 1  = P[1]   +   P[2]   +   ...   +P[n]

É a partir dessa proporção que surge o termo "grupo completo de eventos" Um grupo completo de eventos é a totalidade de todos os eventos exclusivos que formam um determinado espaço de eventos. No caso de um quebra-cabeça, o grupo completo são todas as peças do quebra-cabeça. A probabilidade total de todos esses eventos deve ser necessariamente igual a um, o que significa que um desses eventos deve necessariamente ocorrer como resultado do experimento. Não sabemos qual, mas descobriremos isso com base nos resultados do experimento.

Se pensarmos com cuidado, podemos entender um evento pode ser qualquer conjunto de resultados a partir do espaço de eventos selecionado. Isso significa que um grupo completo pode ser montado por todas as maneiras e combinações possíveis. No caso de um número finito de resultados, pode haver um número limitado de combinações e, no caso de um número infinito, uma quantidade infinita. Se for sabido que o número de resultados é igual ao infinito, então os matemáticos passam a considerar tal conceito como "valor aleatório". Em alguns casos, é até conveniente nos valermos de variáveis aleatórias, porque a tarefa permite isso. Uma variável aleatória é uma maneira ligeiramente diferente de descrever o espaço do evento. Neste caso, o resultado é um conjunto claro de um ou mais números, podemos dizer que é um vetor. No âmbito do modelo que estamos estudando, apresentaremos o conceito de "densidade de probabilidade". 

Acho que vale a pena considerar pelo menos superficialmente esses conceitos, já que precisaremos deles futuramente ao considerar o material restante. A densidade de probabilidade é uma função que descreve todo o espaço de eventos de uma só vez. A dimensão dessa função é exatamente igual ao número de números necessários para descrever cada resultado em um determinado espaço de eventos. Por exemplo, se considerarmos o problema de atirar a um alvo num campo de tiro, então a dimensão desta função será igual a dois, porque o alvo é plano e representa um espaço bidimensional. Nesse caso, as características de um determinado resultado serão as coordenadas X, Y. Esses números são nossas variáveis aleatórias e agora podemos escrever:

• R = R(X,Y)
• R - densidade de probabilidade de uma bala atingir um ponto com coordenadas (X, Y)

As propriedades desta função são tais que a integral completa de menos a mais infinito ao longo de todas as variáveis desta função será igual a um, o que de fato reflete a mesma identidade que estava acima. As probabilidades aqui são determinadas apenas por integrais sobre a região onde a função é apresentada e nada mais. Vários eventos podem ser compostos de regiões integradas por partes e, se desejado, podemos descrever quantos eventos precisarmos, porque seu número é infinito. No âmbito deste artigo, esta definição é suficiente para compreendermos mais no futuro, e acho que não devemos mergulhar mais, porque iremos nos deparar com coisas muito mais sérias, que são absolutamente inúteis no âmbito de nossas tarefas.

Eu gostaria de falar um pouco mais sobre os eventos mútuos. Esses eventos também são muito importantes para uma compreensão geral. É claro que com eventos exclusivos tudo deve ser bastante simples, mas com eventos mútuos tudo é mais complicado. A nível da teoria da probabilidade, temos que lidar com coisas como a combinação ou divisão de eventos, mas não precisamos saber como elas serão, estamos apenas interessados nas probabilidades que serão obtidas como resultado dessas transformações. Para isso, é introduzido o conceito de somas, e produtos de eventos, bem como a operação de inversão. Essas operações não significam a mesma coisa que na matemática comum. Além disso, elas foram projetadas para sere usadas apenas com probabilidades. As probabilidades de eventos mútuos não podem ser somadas, pois neste caso a integridade do grupo não é atendida. Em geral, essas 3 operações com eventos iniciais são capazes de descrever todos os possíveis eventos que podem ser formados a partir de partes de eventos iniciais. Usando o exemplo de dois eventos mútuos, posso mostrar como ficará sobre um plano:

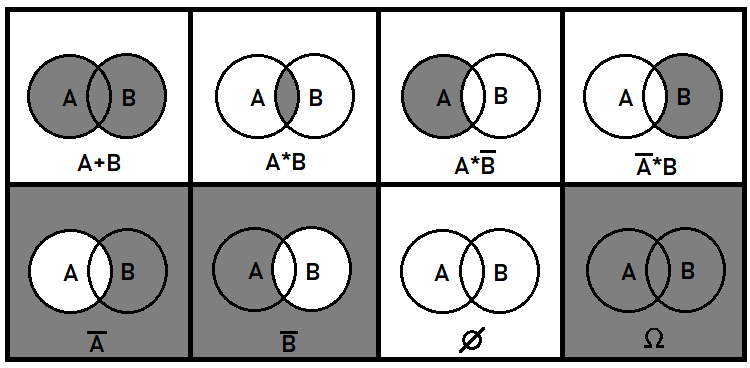
Na verdade, você pode pensar em operações algébricas adicionais, mas elas podem ser compostas pelas já apresentadas. Por exemplo, a divisão booleana equivale à terceira e quarta situações da figura, já que a divisão equivale a multiplicar pelo inverso do evento selecionado. Em geral, estritamente falando, os primeiros dois casos são suficientes para descrever todos os possíveis eventos que podem ser criados a partir de partes dos eventos iniciais. No caso em que mais de dois eventos são mútuos, as coisas se tornam muito mais complicadas. Neste artigo, ainda não faremos uso de eventos mútuos, mas, sim, apenas de exclusivos.

A matemática do mercado é baseada principalmente no conceito de "passeio aleatório". Após o considerarmos, será possível generalizar esses dados em casos de presença de padrões. Vamos começar supondo que abrimos uma posição com um stop-loss e take-profit igualmente espaçados em relação ao preço de abertura, será óbvio para todos que a relação lucro/perda será igual a um se acidentalmente operarmos em diferentes direções ou pontos no gráfico sem considerarmos os spreads, comissões e swaps ou se imaginarmos que a posição é aberta de graça. Em outras palavras, quando a negociação é infinita, o número de posições vencedoras será exatamente igual ao número de posições perdedoras. Com base nesse fato, podemos dizer que obtemos lucro zero, independentemente do tempo de operação; também quando subtraímos as perdas aos spreads, às comissões e aos swaps, descobrimos que estamos estourando dinheiro.

Muitos podem pensar: quer goste ou não, se sei que estou no vermelho, por que devo saber o que é um passeio aleatório e por que preciso da matemática desse processo? Um passeio aleatório pode ajudar a calcular as probabilidades de diferentes eventos. Como o fechamento por stops assimétricos ou o preço médio que vai ser passado numa determinada faixa de preço. Além disso, ajuda a calcular o tempo de vida de uma posição e outros indicadores, que, se não derem uma resposta à questão de onde entrar e onde sair, irão certamente permitir avaliar os riscos ou maximizar/minimizar os lucros e perdas.

Árvores de probabilidade e hipóteses

Um exemplo muito útil para desenvolver seu lobo frontal seria coisas como árvores de eventos ou árvores de probabilidade, o que nós quisermos. Este tópico se origina nos "esquemas de Bernoulli" porque é a base de todas as árvores de probabilidade. Este diagrama examina cadeias de eventos exclusivos que se sucedem. Mas antes de olharmos para isso, vamos dar uma olhada na "fórmula de probabilidade total". É estudando esse importante mecanismo que se pode chegar ao esquema de Bernoulli, e já deste último às árvores de probabilidade. Esta fórmula é assim:

• P(A) = Soma(0 ... i .... n) [ P(H[i]) * P(A|H[i]) ] - probabilidade de evento А
• P(H[i]) — probabilidade de uma hipótese "H[i]"
  
• P(A|H[i]) — probabilidade de que o evento A ocorra no âmbito de uma hipótese "H[i]"

Também gostaria de dizer que, quando se trata de probabilidades, é melhor escrevê-las como hipóteses. Por exemplo, esta entrada "P(H[k]|H[i]) " significaria o seguinte:

1. Probabilidade de evento "H[k]" calculada em relação ao espaço  "H[i]"

Assim, logo entendemos qual evento consideramos um espaço e qual está aninhado. Na verdade, cada evento é outro espaço de eventos mais pequeno e dentro dele pode haver outros eventos aninhados. E, por exemplo, com base nesta lógica, a entrada "P(H[i])" pode ser escrita assim:

• P(H[i]|O) — porque essa probabilidade é considerada em relação a "O".
  

Agora vamos analisar a fórmula da probabilidade total em partes para entender o que está oculto nela. É muito difícil entender isso imediatamente, mesmo assim, logo ficará esclarecido. Vou começar reescrevendo esta fórmula de uma forma ligeiramente diferente:

• P(A) = (S[0] + ... + S[i] + ... + S[n]) / O   =   S[0]/O + ... + S[i]/O + ... + S[n]/O  =  (S[0]/N[0]) * ( N[0]/O ) + ... + (S[i]/N[i]) * ( N[i]/O ) + ... + (S[n]/N[n]) * ( N[n]/O )
• S[i] — área de um segmento específico da interseção da hipótese H[i]
• N[i]  — área de toda a hipótese H[i] (incluindo S[i])
• O  — todos os resultados ou a área de toda a elipse

Após algumas pequenas conversões, que consistiram em multiplicar o numerador e o denominador das frações por "N[i]", podemos ver as probabilidades que estão presentes na fórmula original:

• S[i]/N[i] ----> P(A|H[i])
• N[i]/O ----> P(H[i])

Graficamente, para uma melhor compreensão, tudo isso pode ser representado assim:

 

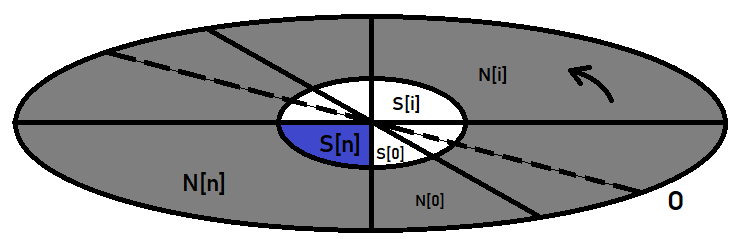
A elipse externa aqui desempenha o papel do espaço de eventos, enquanto a central desempenha o papel do nosso evento, cuja probabilidade estamos procurando. Se imaginarmos que é um relógio, então, tendo desenhado o diâmetro da elipse e girado no sentido anti-horário, vamos cortar nossa elipse em segmentos, que são hipóteses. Uma hipótese é um nome muito especial para eventos, mas na verdade eles são os mesmos eventos que não são diferentes daquele que estamos procurando.

Esta fórmula tem um caso especial que nos ajudará na construção do esquema de Bernoulli. Imagine que a elipse central está inteiramente dentro de uma dessas hipóteses. Em seguida, verifica-se que todos os termos desta soma, que estão relacionados com o resto das hipóteses, são automaticamente zerados, já que a probabilidade de ocorrência do evento "A" no âmbito dessas hipóteses é impossível ou igual a zero. Como resultado:

• P(A) = P(H) * P(A|H)
• H — total probabilidade de exatamente a hipótese dentro da que está localizado o evento selecionado.

Se formos além, podemos supor: "e se o evento "A" também for chamado de hipótese? Assim, uma hipótese é um evento, logo, qualquer evento é uma hipótese". Agora, suponhamos que haja mais um evento "B" que já está dentro de "A", então resulta que "A" é uma hipótese em relação a "B", logo, a fórmula anterior se aplica a esses dois eventos:

• P(B) = P(A) * P(B|A) = P(H) *  P(A|H) *  P(B|A)

Substituindo a relação anterior em vez de "P(A)", já se torna visível um certo padrão de fórmula geral para qualquer número de hipóteses ou eventos aninhados. E por que precisamos disso, você pergunta? Vou responder que este é um protótipo direto da fórmula de Bernoulli, que analisaremos um pouco a seguir, mas por enquanto analisaremos algo muito curioso.

Fractais

Se aderirmos à lógica acima, descobriremos que se P(A) + P(B) = 1, então este é um grupo completo de eventos, e acontece que um grupo completo pode ser coletado a partir de dois cadeias arbitrárias de hipóteses que estão aninhadas entre si. Mas essas hipóteses podem ser mutuas, e se exigirmos que todas as possíveis hipóteses aninhadas sejam exclusivas em relação às hipóteses de outras cadeias, isso causará automaticamente que todas as cadeias serão exclusivas em relação a outras cadeias no espaço de eventos dado. Se pensarmos cuidadosamente sobre como ficará no gráfico, teremos uma formação muito interessante:

Esta formação é chamada de "Fractal", e tudo porque é impossível construir tal estrutura até o fim, ela pode ser construída indefinidamente. No meu desenho, ela é construída com apenas 3 níveis de profundidade. Os retângulos azuis representam o fim de uma cadeia de probabilidades separada. O mais interessante é que, se somarmos as probabilidades de todas essas cadeias, elas formarão um grupo completo de eventos.

As "combinações" são adequadas para descrever esses fractais. As combinações são construídas com base no conceito de "fatorial". Também existe o conceito de "permutação", que se situa entre o conceito fatorial e o de combinação. A fórmula de permutação é derivada da fórmula fatorial, e a fórmula de permutação implica o conceito de combinação. Vou apresentar essas fórmulas:

• n! - fatorial do número "n"
• P(n,k) = n! / ( n - k )!  — permutações de elementos "N" por elementos "K"
• С(n,k) = n! / ( k! * ( n - k )! )  — combinações de "N" elementos a partir de "К" elementos

Acho que não é segredo para ninguém que o fatorial é o produto de todos os números naturais que começam com "1" e terminam com um número "n", enquanto "0! = 1". Ou seja, o fatorial de zero é igual a um, neste caso é apenas uma exceção à regra, mas na verdade, não vi um único caso em que essa exceção interferisse nos cálculos ou complicasse os algoritmos, muito pelo contrário.

As permutações são um pouco mais complicadas. Imagine que você tem um baralho que tem um certo número de cartas, e nós ideamos uma experiência simples: temos que embaralhar as cartas e remover várias de uma forma completamente arbitrária e distribuí-las sobre a mesa pela ordem em que foram retiradas do baralho. Assim, as permutações são o número de resultados possíveis de uma determinada experiência, enquanto a ordem das cartas também é considerada um identificador único de um resultado específico. É claro que isso se aplica não apenas a experiências com mapas, mas a qualquer coisa, até mesmo pedras ou lápis.

A primeira carta pode ser retirada do baralho de "n" formas, a segunda, de "n-1" formas, uma vez que a primeira carta retirada do baralho não está mais nele, e assim por diante até "n-k-1". Acontece que, para obter o número total de possíveis permutações, precisamos multiplicar todos esses números, desde "n-k-1" até "n". É claro que isso nos lembra o fatorial. Se pegarmos "n!" e o dividirmos pelos últimos "nk" fatores, obtemos o produto inicial; ele é exatamente igual a "(n-k)!". É assim que obtemos a famosa fórmula de permutação.

A fórmula da combinação é um pouco mais complicada, mas também é muito fácil de deduzir. Agora vamos pensar um pouco que se encontrarmos todas as permutações possíveis não importa para nós a ordem dos elementos, mas, sim, as cartas que calharam neste conjunto. Agora precisamos encontrar o número total de casos em que obtivemos um conjunto de cartas ligeiramente diferente. Na verdade, cada permutação já contém um desses conjuntos independentes, mas não precisamos de todos eles. Agora vamos mudar um pouco nossa lógica, vamos tentar coletar todas as permutações de todas as combinações possíveis: acontece que se tomarmos uma combinação, não importa como reorganizemos os elementos nela, cada uma dessas permutações irá única. Além disso, se pegarmos todas essas combinações únicas e fizermos nelas todas as possíveis permutações de elementos, apenas obteremos todas as permutações possíveis, e acontece que:

• P(n,k) = C(n,k) * P(k,k)

O número total de permutações únicas dentro de uma combinação é simplesmente igual a "P(k,k)", porque precisamos encontrar a partir das variantes "k" todas as permutações possíveis para as mesmas variantes "k". A partir disso, pode-se ver que dividindo ambos os lados da equação por P(k,k)", podemos obter a fórmula de combinação que estamos buscando:

• C(n,k) = P(n,k)/P(k,k) = n! / ( k! * ( n - k )! )
  

Ambas as permutações e combinações são amplamente utilizadas na teoria da probabilidade, mas se falamos sobre a aplicação prática na negociação, são as combinações que serão extremamente úteis para nós. São usados para construir funções fractais com uma diversidade de propósitos. Talvez fosse mais correto chamá-las de recorrentes, mas por alguma razão eu chamo tais funções de fractais, provavelmente porque são realmente fractais, toda uma árvore de chamadas.

Esquema de Bernoulli

Antes de começarmos a considerar tais funções fractais, devemos considerar esta fórmula. Vamos imaginar que temos uma cadeia de experiências idênticas que temos que repetir várias vezes. Como resultado de cada experiência, um evento deve aparecer, ou não, com certa probabilidade. Além disso, suponhamos que desejamos encontrar a probabilidade de que numa cadeia de "n" experiências nosso evento apareça "k" vezes. A fórmula de Bernoulli pode responder a esta pergunta:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)   — fórmula de Bernoulli
  
• p  — probabilidade de um evento ocorrer como resultado de uma única experiência
• q = 1 - p   — probabilidade de o evento não ocorrer como resultado de uma experiência

Recordando a fórmula que derivamos para cadeias probabilísticas, vamos estendê-la para o caso de uma cadeia arbitrariamente grande:

• P(n) = P(H[1]|O) *  P(H[2]|H[1]) *  P(H[3]|H[2]) * ... * P(H[k]|H[k-1]) * ... *P(H[n]|H[n-1])
• n  — número de segmentos da cadeia
• O  — todo o conjunto de resultados também pode ser denotado como H[0]

Essa fórmula calcula a probabilidade de que aconteça exatamente a cadeia de hipóteses de que precisamos. Visualmente, podemos representar essa fórmula da seguinte maneira:

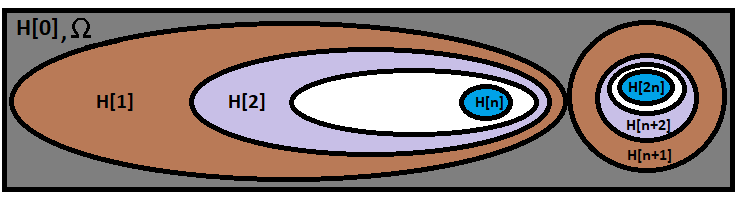
Na elipse maior está nossa fórmula, enquanto na menor há una cadeia exclusiva em relação à nossa cadeia, ela simboliza algum outro ramo de uma combinação diferente. Existem tantos ramos quantas opções para calcular combinações em nossa fórmula. Só não confunda as combinações em si com as variantes para calcular combinações. O número de variantes para calcular combinações é:

• n+1 (porque também são consideradas as combinações de "0" resultados bem sucedidos)
• n  — número de experimentos independentes numa cadeia de experiências

Agora imaginemos que as probabilidades de todas essas hipóteses são iguais a "p" ou "q". Então, a fórmula é simplificada:

• P(n) = Pow(p,k)*Pow(q,n-k)
• k  — número de fatores iguais a "p" presentes no produto
• n-k  — número de fatores iguais a "q" presentes no produto

A semelhança com a fórmula de Bernoulli já é visível, só falta a combinação. Mas se pensarmos com cuidado, fica claro que as variantes das cadeias com semelhante probabilidade e número de "k" e "n-k" são iguais a "C(n,k)". Como todas essas cadeias de probabilidades são exclusivas, verifica-se que a probabilidade de obtermos qualquer uma delas será igual à soma das probabilidades de todas elas. E como essas probabilidades são idênticas, podemos multiplicar a probabilidade de uma cadeia pelo seu número, e obtemos nossa fórmula de Bernoulli:

• P = C(n,k)*Pow(p,k)*Pow(q,n-k)

É interessante que esta fórmula também pode ser estendida, por exemplo, para aqueles casos em que é necessário encontrar a ocorrência de um evento "k" ou mais vezes, "k" ou menos vezes, bem como todas as variações possíveis sobre este tema. Nesse caso, haverá a soma das probabilidades para as combinações de que precisamos. Por exemplo, a probabilidade de o evento ocorrer mais do que "k" vezes será calculada da seguinte forma:

• P = Summ(k+1 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i)]

Também é muito importante entender que:

• P = Summ(0 ... i ... n)[C(n,i)*Pow(p,i)*Pow(q,n-i) ] = 1

Em outras palavras, todas as possíveis cadeias formam um grupo completo de eventos exclusivos. E também uma identidade muito importante:

• Summ(0 ... i ... n)[C(n,i)] = Pow(2,n)
  

Acho que isso é lógico, dado que cada segmento da cadeia de probabilidade tem apenas dois estados - "o evento aconteceu" e "o evento não aconteceu" O estado em que o evento não aconteceu é exatamente o mesmo evento, só que algo diferente aconteceu.

As combinações também têm uma propriedade muito interessante:

• C(n,k) =  C(n,n-k)
  

Podemos chegar a isso, considerando isso igua a "C(n,n-k)" e comparando com "C(n,k)". Após algumas pequenas conversões, veremos que ambas as expressões são idênticas. Esbocei um pequeno programa MathCad 15 para testar todas as afirmações acima:

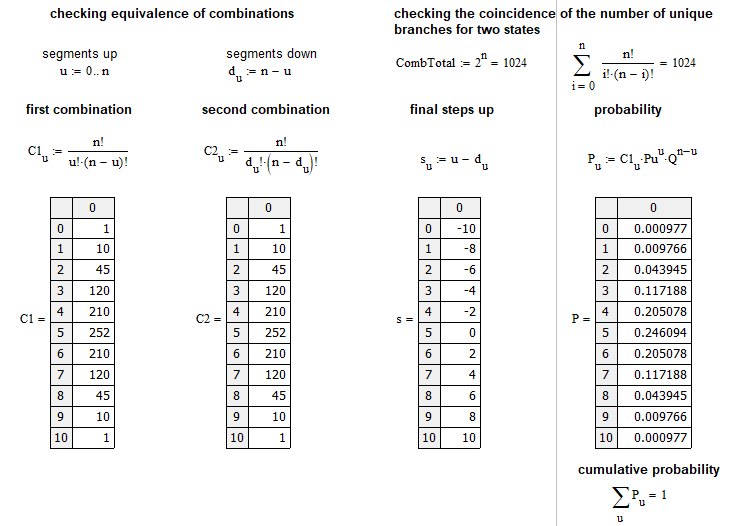
Fiz este exemplo próximo ao mercado e nele é calculada a probabilidade de que fora de "n" etapas o mercado se move "u" etapas para cima. Uma etapa é um movimento de preço para baixo ou para cima ao longo de um certo número de pontos em relação à etapa anterior. Graficamente, a matriz de probabilidades para cada "u" pode ser traçada assim:

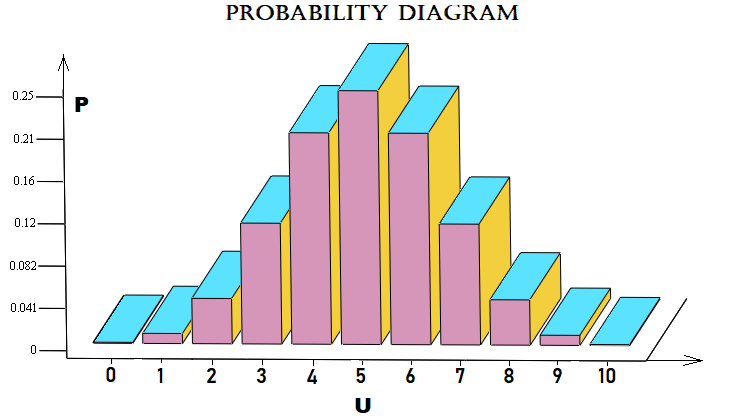
Neste caso, para simplificar, usei um esquema de Bernoulli com "10" etapas. O arquivo será anexado ao artigo e quem quiser pode mexer nele à vontade. Nem sempre temos que aplicar este esquema de formação de preços, ele também se aplica a ordens ou qualquer coisa.

Criando o primeiro fractal

Questões relacionadas ao stop-loss e take-profit exigem um estudo separado. Acho que todos estão interessados em como calcular a probabilidade de fechar um trade usando stop-loss ou take-profit, quando os valores desses stop-loss e take-profit são conhecidos em pontos (distância em relação ao preço atual). Esse valor pode ser calculado em qualquer ponto, mesmo que não se trate do preço de abertura, pois tudo isso depende diretamente dos mecanismos de precificação. Neste exemplo, quero demonstrar a fórmula usando fractais. No caso de um passeio aleatório, essa probabilidade pode ser calculada da seguinte forma:

• P(TP) = SL / ( TP + SL ) — probabilidade de um take-profit ser acionado
• P(SL) = TP / ( TP + SL ) — probabilidade de um stop-loss ser acionado
• SL  — distância em pontos até o stop-loss
  
• TP  — distância, passeio em pontos até o take-profit

Acho que todos entendem que essas duas probabilidades formam um grupo completo:

• P(TP) + P(SL) = 1
  

Esta fórmula implica que, no caso de negociação aleatória, o valor esperado de todas essas estratégias será zero, se não levarmos em consideração o spread, comissão, swap:

• M =  P(TP) * TP - P(SL) * SL = 0

Este é o caso mais simples quando abrimos com stops fixos, mas se desejar, tudo isso pode ser generalizado para absolutamente qualquer estratégia, e agora vamos provar essa fórmula usando o mesmo MathCad 15. Trabalho com este programa há muito tempo, ele permite realizar cálculos de quase qualquer complexidade, mesmo com o uso de programação. Neste exemplo, não apenas provaremos as fórmulas que escrevi acima, senão que também veremos o primeiro exemplo de construção de uma função fractal. Vamos começar esboçando nosso processo de movimento de preços conforme o representamos. Aqui não podemos usar funções contínuas, só discretas. Para fazer isso, pegamos nossa ordem e adiamos nossas distâncias (stops) para cima e para baixo, após isso, dividimos esses segmentos em partes com etapas iguais, de modo que cada segmento se encaixe num número inteiro de etapas, e imaginamos que o preço se move ao longo dessas etapas. Nesse caso, é óbvio que, como as etapas são todas iguais, a probabilidade de uma etapa em qualquer uma das duas direções é exatamente "0,5". Para implementar o fractal correspondente, precisamos de uma ilustração:

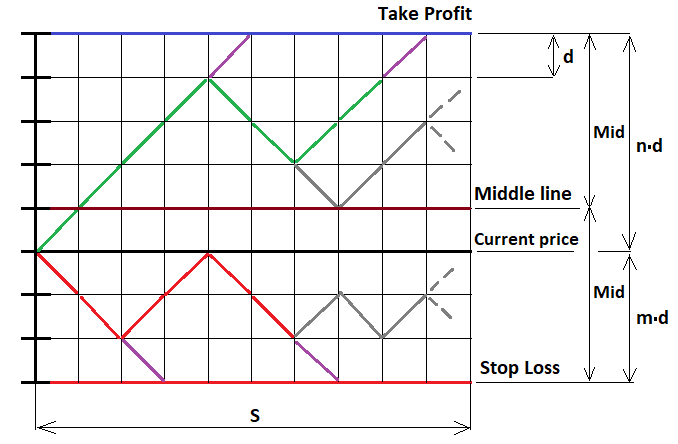
Para resolver este problema, devemos considerar possíveis três casos de continuação do fractal:

1. Estamos acima da linha do meio (U > MiddleLine)
2. Estamos abaixo da linha do meio (U < MiddleLine)
3. Agora estamos no nível da linha média (U = MiddleLine)

O papel de "U" aqui é o número total de etapas "u-d" para cima, em relação ao preço de abertura, se o ponto a partir do qual vamos continuar construindo o fractal está abaixo desse preço, então esse valor assume valores negativos de acordo com a fórmula. Se estivermos na linha do meio, o número de etapas que podemos dar sem medo de cruzar a linha é exatamente um a menos que "Mid". Mas antes de prosseguir com a construção, devemos definitivamente limitar a construção do fractal ao número de etapas que o preço ou as ordens podem realizar. Se o número de etapas exceder o exigido, somos obrigados a interromper sua construção. Caso contrário, teremos uma recursão infinita, da qual será impossível sair, e o tempo de cálculo será igual ao infinito.

Na figura, desenhei várias etapas roxas, nesses pontos coletamos as probabilidades e as somamos numa variável comum, e depois disso devemos virar nossa cadeia para cima ou para baixo, dependendo de qual borda nossa cadeia se encosta para que ela possa continuar avançando e construindo novos níveis fractais aninhados. No outros pontos, podemos construir livremente níveis fractais completos com base no esquema de Bernoulli, que discutimos acima.

No caso em que podemos construir uma árvore com base no esquema de Bernoulli, devemos antes de tudo determinar o número de etapas que podemos fazer, levando em consideração os casos extremos em que todas as etapas são exclusivamente para cima ou para baixo. Para todos os três casos, esse valor assume os valores:

• (n - 1) - U  — nossa cadeia já está acima da linha média (uma vez que um aumento em U acarreta uma diminuição na distância até o limite superior)
• (m - 1) + U  — nossa cadeia está abaixo da linha central (uma vez que uma diminuição em U acarreta uma diminuição na distância até o limite inferior)
• (floor(Mid)-1)  — nossa cadeia está exatamente na linha média
• n — número de segmentos superiores
• m — número de segmentos inferiores
• floor — função que descarta a parte fracionária do número (talvez isso não seja necessário por enquanto)

Neste caso, primeiro precisamos calcular dois magnitudes auxiliares:

• Mid = (m+n)/2  — metade da largura do canal (em etapas)
• Middle = (m+n)/2 - m   — valor "U" para a linha média (em etapas)

Esses valores serão úteis no futuro para descrever a lógica de ramificação do fractal. Até agora, construiremos apenas um fractal para os casos "n>=m". Mas esses dados ainda são insuficientes para a construção correta do fractal. Para poder construir níveis mais profundos do fractal, é necessário redefinir "U" para cada nova combinação do esquema de Bernoulli e transferi-lo para um novo nível fractal. Além disso, é necessário incrementar corretamente o número de etapas realizadas e também transferi-las corretamente mais para frente. Da mesma forma, teremos que coletar a probabilidade de toda a cadeia usando os multiplicadores do próximo nível fractal e transferir a probabilidade da cadeia intermediária para o próximo nível até que este processo termine com um cruzamento bem-sucedido da borda desejada. Para um melhor entendimento, criei uma ilustração para todas as três variantes:

  

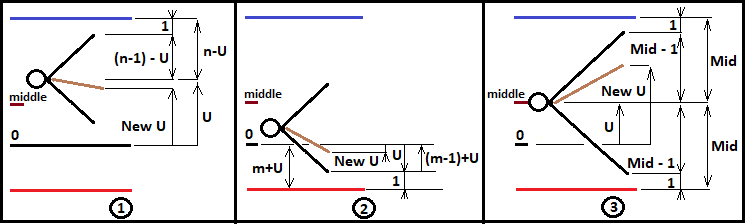
Guiados por este diagrama, podemos agora escrever quais serão os valores "NewU" e outros valores auxiliares para cada caso de todos os apresentados, vamos considerar isso usando o exemplo de construção de um fractal para calcular a probabilidade de cruzamento do limite superior:

Para o caso 1:

Vamos dar uma olhada na imagem superior e descrever matematicamente o que está acontecendo lá. Esta imagem é um extrato do meu programa no MathCad 15. Não dei a listagem completa, quem quiser pode vê-la no apêndice do artigo. Também precisamos nos lembrar de que o primeiro retângulo está num loop e itera com base em "i" para descrever todas possíveis as combinações. Essa lógica, se desejado, pode ser repetida no ambiente de desenvolvimento do MetaEditor. Vamos começar com a primeira ilustração do diagrama. Para definir "NewU", primeiro precisamos definir algumas fórmulas fundamentais que nos ajudarão com isso:

• ( n - 1 ) - U = f — este valor, neste caso, é o número de etapas da futura árvore de combinação (o tamanho é determinado pela distância até a borda mais próxima do canal fractal)
• u + d = f  — mesmo valor, expresso em termos do número de segmentos crescentes e decrescentes
• s = u - d  — número de etapas finais para cima, expresso em termos de segmentos decrescentes e crescentes
• u = i  — visto que no meu programa ele é iterado exatamente de acordo com "i" (só precisamos nos lembrar disso)

Para calcular todas as quantidades necessárias, precisamos expressar "s" através de "U" e "i", vamos direto ao assunto. Para fazer isso, precisamos apenas excluir a variável "d". Primeiro, nós o expressamos e, em seguida, o substituímos na expressão por "s":

1. d = f - u = f - i = ( n - 1 ) - U - i
2. s = i -( n - 1 ) + U + i = -( n - 1 ) + 2*i + U

Em seguida, usando a expressão encontrada para "s", buscamos "NewU" e todas as magnitudes de que precisamos para transmissão para o próximo nível fractal:

• NewU = s + U = -( n - 1 ) + 2*i + 2*U   - nosso novo "U" para transmissão para o próximo nível fractal
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( n - 1 ) - U ,i) * Pow(p,i) * Pow(1-p,( n - 1 ) - U -i)  — nossa nova probabilidade da cadeia "P" para transmissão para o seguinte nível fractal (obtemos multiplicando pela probabilidade de um novo segmento da cadeia)
• NewS = S + f = S + ( n - 1 ) - U  — nosso novo "S" para transmissão para o próximo nível fractal

Agora vamos dar uma olhada no retângulo inferior. Nele, tratamos dos casos em que a cadeia de etapas atinge o limite superior do canal. Precisamos processar dois casos:

1. Coleta da probabilidade de uma cadeia que se cruza com uma borda (esta ação está sublinhada em vermelho)
2. Ações semelhantes para incrementar novos valores que passaremos para o próximo nível fractal

Este caso é muito simples, porque existem apenas dois casos possíveis:

1. Contato com a borda
2. Reversão a partir da borda

Para cada uma dessas ações, não precisamos de um esquema de Bernoulli, porque neste caso há apenas uma etapa. A propósito, a probabilidade de uma reversão é multiplicada precisamente por "(1-p)", pois a probabilidade de interseção é de "p", e esses dois eventos devem formar um grupo completo, como já deveríamos ter entendido nos baseando nos cálculos anteriores. Naturalmente, aumentamos os passos em "1", e "U" diminuímos em "1", porque o reflexo está para baixo e precisamos diminuir esse valor. Isso é tudo de que precisamos para construir adequadamente este caso. Essas regras serão quase idênticas na hora de construir os fractais básicos dos que precisaremos para propósitos completamente diferentes.

Para o caso 2:

Para este caso, o cálculo é quase idêntico, a única diferença é que "f" já assume um valor diferente:

• ( m - 1 ) + U = f

Da mesma forma, expressamos "s" por meio de "U" e "i", usando as mesmas fórmulas do caso anterior:

1. d = f - u = f - i = ( m - 1 ) + U - i
2. s = i -( m - 1 ) - U + i = -( m - 1 ) + 2*i - U

Da mesma forma, encontramos todas as quantidades de que precisamos para transmissão para o próximo nível fractal:

• NewU = s + U = -( m - 1 ) + 2*i  - nosso novo "U" para transmissão para o próximo nível fractal
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( ( m - 1 ) + U ,i) * Pow(p,i) * Pow(1-p,( m - 1 ) + U -i)  — nossa nova probabilidade da cadeia "P" para transmissão para o seguinte nível fractal
• NewS = S + f = S + ( m - 1 ) + U  — nosso novo "S" para transmissão para o próximo nível fractal

O retângulo inferior aqui é quase idêntico ao caso anterior, exceto que aumentamos o "U" em um, uma vez que o reflexo sobe, e isso significa um aumento em "U". É importante notar também que neste caso não há coleta de probabilidades, pois neste fractal não estamos interessados nos casos de interseções com o limite inferior. Resta apenas analisar o último caso, quando o canal atinge a linha média do canal.

Para o caso 3:

Definimos "f":

• floor(Mid) - 1 = f

Encontramos "s":

1. d = f - i =  floor(Mid) - 1 - i
2. s = i - d = -(floor(Mid) - 1) + 2*i

Finalmente, encontramos os valores a serem transferidos para o próximo nível fractal:

• NewU = s + U = -(floor(Mid) - 1) + 2*i + U
  
• NewP = P * C(f,i) * Pow(p,i) * Pow(1-p,f-i) = P * C( floor(Mid) - 1 ,i) * Pow(p,i) * Pow(1-p,floor(Mid) - 1 - i)  — nossa nova probabilidade da cadeia "P" para transmissão para o seguinte nível fractal
• NewS = S + f = S + (floor(Mid) - 1) — nosso novo "S" para transmissão para o seguinte nível fractal

Uma característica distintiva deste caso é que nenhuma coleção de probabilidades ocorre neste bloco, porque esta coleção é possível apenas nos valores de fronteira de "U", onde as cadeias de probabilidade também são refletidas de volta para o canal para que possam se espalhar mais. A construção de um fractal para calcular a probabilidade de cruzamento com o limite superior será idêntica, com a única diferença de que a coleta de probabilidades não ocorrerá no primeiro caso, mas, sim, no segundo.

Uma característica interessante da construção desses fractais é a presença obrigatória da fórmula de Bernoulli. As combinações são destacadas em rosa e os produtos das probabilidades, em amarelo. Juntos, esses dois fatores formam a fórmula de Bernoulli.

Agora vamos verificar simultaneamente a construção de todo o fractal e a suposição de que o valor esperado de lucro depende apenas da capacidade preditiva. As etapas podem ser representadas como pontos e como trades, no último caso, os pontos simplesmente precisam ser multiplicados pelo devido coeficiente de proporcionalidade, que depende dos lotes e do tamanho do tick, mas neste caso veremos como ficará em pontos, porque tal representação é universal:

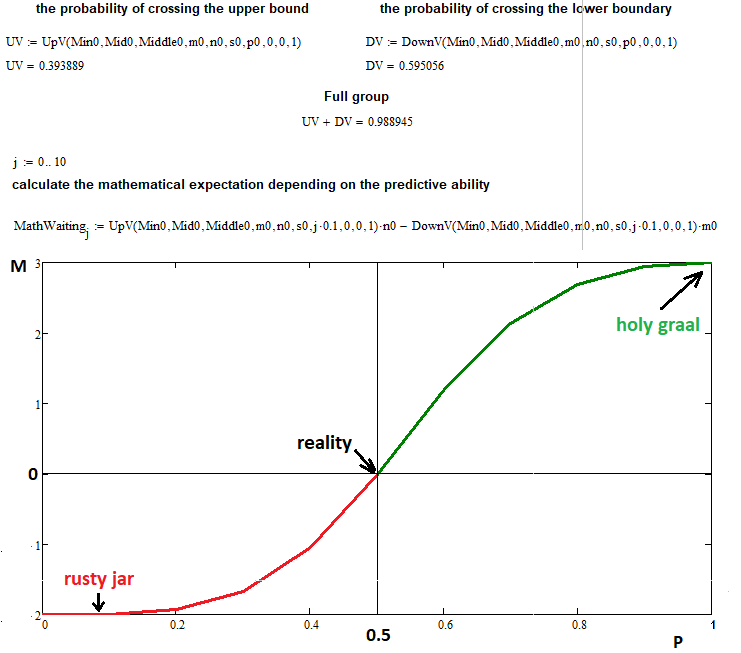
Neste exemplo, usei os seguintes dados de entrada para representar graficamente o valor esperado versus a probabilidade de uma etapa crescente:

• n = 3 — número de segmentos superiores
• m = 2  — número de segmentos inferiores
• s = 22  — número de etapas permitidas para uma reação em cadeia de uma função fractal (se for aumentado, será muito difícil para o computador suportá-la, mas este número de etapas é suficiente para obter suficiente precisão)
• 0 ... 0.1 ... 0.2 ...... 1.0   — divide a faixa de probabilidades da etapa em "10" partes com uma etapa igual a "0,1"

Como você pode ver, com uma probabilidade igual a "0,5", o valor esperado de nossos negócios é exatamente zero, conforme previsto pela fórmula que provamos usando este fractal. Nos pontos extremos "0" e "1", podemos ver que o valor da função tende a "n" e "-m", o que é totalmente consistente com nossas suposições. O fractal resolveu com sucesso sua tarefa, embora tenha revelado uma desvantagem completamente previsível: uma complexidade e um tempo de computação que aumentam imensamente. Se for necessário, acho que esperar uma ou duas horas, até um dia, não é tão difícil, já que só assim é possível resolver muitos problemas.

Também gostaria de dizer que este fractal só funcionará para os casos em que "n> = m", ou seja, quando a remoção do limite superior do ponto de partida for maior do que a remoção do limite inferior, mas não precisamos considerar essas coisas no fractal. Este design é espelhado no sentido de que se de repente "n < m", podemos simplesmente calcular esse fractal passando "m" em vez de "n" e "n" em vez de "m", e depois disso trocar de lugar as probabilidades e obter um reposicionamento simples de dois valores, tudo isso é feito de maneira muito fácil. Esses fractais podem ser usados não apenas para provar algumas fórmulas, mas também para reverter o processo. Algumas fórmulas só podem ser obtidas com o uso de fractais.

Conclusões

Se estudarmos cuidadosamente este material, acredito que retiramos as seguintes conclusões relevantes:

• Ao usar teoria da probabilidade juntamente com programação, podemos ter uma base teórica para descrever muitos dos processos no mercado.
• Confirmamos que os fractais, em conjunto com as principais disposições da teoria da probabilidade, podem fornecer respostas às perguntas mais difíceis.
• Analisamos completamente um exemplo de construção de um fractal bastante complexo.
• Toda a teoria foi testada na prática usando programação no ambiente MathCad 15.
• Está provado que o esquema de Bernoulli oferece oportunidades para a construção de quaisquer fractais com dois estados de etapa.

Conclusão

Espero que o leitor deste material tenha conseguido ver algo novo e útil para uso prático na negociação. Ao desenvolver este artigo, tentei transmitir todo o poder da matemática discreta e da teoria da probabilidade a fim de prepará-lo para a difícil tarefa de descrever processos de mercado usando cadeias de probabilidade fractal. Tentei combinar todas as principais disposições da teoria da probabilidade, o que nos ajudará a resolver os problemas mais difíceis de aplicação prática na negociação, e também tentei descartar o que é supérfluo e pode nos confundir. No próximo artigo, veremos novos exemplos da aplicação prática dos fractais e respostas a outras questões igualmente importantes.