Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler

İçindekiler

• Giriş
• Olasılık teorisi piyasa analizinde nasıl faydalı olabilir?
• Manuel ve otomatik ticaret için uygulamalı olasılık teorisinin özellikleri
• Olasılık ağaçları ve hipotezler
• Fraktallar hakkında
• Bernoulli şeması
• İlk fraktalın oluşturulması
• Özet
• Sonuç

Giriş

Bence olasılık teorisinin dili, piyasanın içerisinde işleyen süreçlerin tamamen farklı bir düzeyde anlaşılmasını sağlayabilir. Olasılık teorisinin özelliklerini anladıktan sonra, tamamen yeni bir şekilde düşünmeye başlayacaksınız. Belirsiz fikirler veya kanıtlanmamış bazı ipuçları artık acele etme ve gerçek bir hesapta işlem yapma isteğine neden olmayacaktır. Öte yandan, bu yeni yaklaşımın herkes için rahat olmayabileceğini de anlıyorum. Bu seride, size ticarete gerçek ve doğru bir yaklaşım göstermek istiyorum. Tüm kararlar yalnızca rakamlara dayandırılmalı ve "belki", "ya olursa", "öyle görünüyor" ve benzeri varsayımlardan kaçınılmalıdır.

Olasılık teorisi piyasa analizinde nasıl faydalı olabilir?

Hayatımın oldukça uzun bir döneminde teknik bilimle uğraştım, olasılık teorisi ise benim için en zor olanıydı. Bunun nedeni, olanaklarının ne kadar geniş olduğunu anlamamış olmamdı. Tartışılmaz avantajı, yalnızca yaratıcılığınıza, çalışkanlığınıza ve tabii ki zekanıza bağlı olan sınırsız yetenekleridir. Yıllarca teknik çalışmalar yaptıktan sonra, zekanın aynı tür işlemleri yaparken gösterdiğiniz hız ve dikkatle değil, zihninizin esnekliğiyle ilgili olduğunu fark ettim. Örneğin diferansiyel matematiği, vektör ve skaler alanlar teorisini ve hatta okul cebirini ele alırsak, bunların hepsi neredeyse her sorunu çözebileceğiniz belirli bir dizi kural veya öneri vardır. Standart olmayan her görev beynimiz için bir şoktur. Olasılık teorisinde, bu türden sonsuz sayıda an vardır - bu, birçok problemin yalnızca tamamen farklı yaklaşımlarla çözülebileceği yerdir. Başka bir deyişle, zeka ancak belirli bir problemi çözmek için gösterilen gayret ve istekle geliştirilebilir ve olasılık teorisi bu konuda size yardımcı olabilir.

Olasılık teorisinin çerçevesi, matematiksel beklenti, çeşitli olayların olası olasılıkları, ortalama değerler, yüzdelik dilimler vb. gibi temel ticaret kavramlarını açıklar. Olasılık teorisi, mükemmel bir ticaret sistemi olmadığını ve her sistemin kendi riskleri olduğunu iddia eder. Yapabileceğimiz şey, yalnızca riskleri çok fazla sıkıntıya neden olmayan ticaret sistemini seçmektir. Asıl önemli olan bu riskleri doğru yorumlamaktır. Başka bir deyişle, kesin olmayan duyumlar veya görsel yaklaşımlar dilinden net nicel kriterlere geçiyoruz. Elbette görsel değerlendirmeler de önemlidir, ancak nicel değişkenlerle birleştirildiklerinde daha iyi sonuç verirler. Tüm detayları ve nüansları tek bir makalede anlatmak imkansız, ancak burada bazı ilginç bilgilere yer vermeye çalışacağım. Umarım burada işinize yarayacak bir şeyler bulursunuz.

Manuel ve otomatik ticaret için uygulamalı olasılık teorisinin özellikleri

Olasılık teorisini piyasa analizi için kullanmaya başlamadan önce, öncelikle olaylar ve olasılıkları hakkında bilgi sahibi olmamız gerekir. Bir olay, bazı kriterleri karşılayan veya bazı kriterlere göre belirli bir kümede gruplandırılan bir dizi sonuçtur. Bir sonuç, verilen gruptaki diğer tüm elemanlara eşit olan belirli bir temel elemandır. Grup, bir sürecin tüm olası sonuçlarını ifade eder. Bunun ne tür bir süreç olduğu, fiziğinin ne olduğu veya sürecin ne kadar sürdüğü çok önemli değildir. Önemli olan, bu sürecin sonucunda, süreç tamamlanmadan önce var olmayan bir şeyi elde edecek olmamızdır. Olayımızla ilgili olan bu sonuçlar esasen bizim olayımızdır - kolaylık sağlamak için bunları tek bir nesnede birleştiriyoruz. Yukarıdaki fikir aşağıdaki gibi görselleştirilebilir:

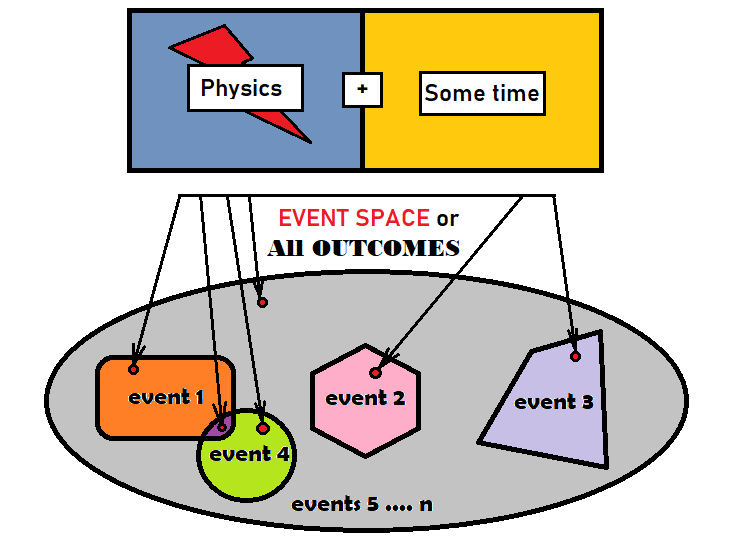
Yukarıdaki şekildeki gri elips tüm sonuçlar olarak işlev görür. Matematikte buna olay uzayı denir. Bu, olay uzayının geometrik bir şekle sahip olduğu anlamına gelmez, ancak bu kavramları tanımlamak için oldukça uygundur. Elipsin içinde 4 olay vardır. Şekilden de görülebileceği gibi, her olayın içinde küçük bir kırmızı nokta vardır. Bu tür noktalar sınırlı veya sınırsız sayıda olabilir - bu, söz konusu sürece bağlıdır. Şekildeki olaylardan ikisi kesişmektedir. Bu tür olaylar örtüşen olaylar olarak adlandırılır. Dolayısıyla, her iki olaya da ait olan bazı sonuçlar vardır. Diğer tüm olaylar elipsin farklı yerlerinde bulundukları ve geometrik olarak kesişmedikleri için örtüşmezler. Gri alanın geri kalanı son olay olarak kabul edilebilir veya gri alan kalmayana kadar daha küçük parçalara da ayrılabilir.

Her olayın, genellikle olasılık olarak adlandırılan en az bir karşılık gelen sayısı vardır. Olasılık, aynı deneyi sonsuza kadar üretebilseydik, aynı sürecin tekrarları sırasında bu olayın ne sıklıkta ortaya çıkacağı anlamına gelir. İki tür olay uzayı bulunmaktadır:

1. Sonlu sayıda olası sonuç ile
2. Sonsuz sayıda olası sonuç ile

Eğer sonuç sayısı sonlu ise, olasılık aşağıdaki gibi hesaplanabilir:

• P = S/N - S olay kriterini karşılayan sonuçların sayısı, N ise olay uzayındaki tüm sonuçların toplam sayısıdır

Bazı durumlarda, belirli bir uzaydaki sonuç sayısı sonsuz olduğunda, bu olasılık örneğin integraller kullanılarak da belirlenebilir. Yukarıdaki görüntüdeki durum için, "S" ve "N" değerleri geometrik şekillerinin alanları ile değiştirilebilir.

Olay uzayının ne olduğunu açıkça tanımlamak, sonuçların sayısını ve olaylar tarafından tanımlanan fiziği tanımlamak her zaman mümkün değildir. Bu grafiksel temsiller beynimizin verileri değerlendirmesine yardımcı olmalıdır, böylece beyin bazı geometrilerle çalışmak yerine, neler olup bittiğini anlamaya çalışarak, sadece olasılıklar ve bu olasılıklara karşılık gelen ek sayılarla çalıştığımız fikrine alışabilir. Olaylar aynı zamanda durumlar olarak da adlandırılabilir. Durumlar mantığını kullanırsak, olasılık tam olarak aynı deneylerin tekrarlanması sonucunda belirli bir durumun ortaya çıkma sıklığıdır. 

Şekillerin alanlarına benzer şekilde, elipse dahil olan tüm şekillerin alanlarının toplamı tam olarak bu elipsin alanına eşittir. Matematik açısından alan, oraya düşen sonuçların sayısıdır. Dolayısıyla:

• N = S[1]+S[2]+...+S[n]
  
• S - belirli bir olayın sonuçlarının sayısı
• N - olay uzayının tüm sonuçları

Eşitliğin her iki tarafını da N değerine böldüğümüzde, tüm olasılık teorisinin temelini oluşturan ilginç ve çok önemli bir ilişki elde ederiz:

• 1 = S[1]/N+S[2]/N+...+S[n]/N

Bu oranın yalnızca örtüşmeyen olaylar için geçerli olduğunu lütfen unutmayın. Çünkü olaylar birleşirse, şekil alanları üst üste biner (örtüşür) ve alanlarının toplamı orijinal elipsin alanından daha büyük olur. Tüm yapboz parçalarının alanının ortaya çıkan görüntüye tam olarak eşit olduğu bir yapboza benzer. Bu durumda, bir yapboz parçası olaylardan birini temsil eder. Tüm bu kesirler belirli olayların olasılıklarını temsil eder:

• 1 = P[1]+P[2]+...+P[n]

Bu oran, kolektif kapsamlı olaylar kümesi teriminin temelini oluşturmaktadır. Kolektif kapsamlı olaylar kümesi, belirli bir olay uzayını oluşturan tüm örtüşmeyen olayların birliğidir. Bir yapboz için, kolektif kapsamlı küme tüm yapboz parçalarıdır. Tüm bu olayların toplam olasılığı bire eşit olmalıdır, bu da bu olaylardan birinin deney sonucunda mutlaka gerçekleşmesi gerektiği anlamına gelir. Hangi olayın gerçekleşeceğini bilmiyoruz, ancak bunu deneyin sonucundan öğreneceğiz.

Yukarıdakilere göre, seçilen olay uzayındaki herhangi bir sonuç kümesi bir olay olarak hizmet edebilir. Bu, kolektif kapsamlı kümenin mümkün olan tüm yollarla ve kombinasyonlarla bir araya getirilebileceği anlamına gelir. Sonlu sayıda sonuçla uğraştığımızda, bu tür kombinasyonların sayısı sınırlı olabilir; sonsuz sayıda sonuç için kombinasyon sayısı her zaman sonsuz olacaktır. Sonuç sayısının sonsuza eşit olduğu biliniyorsa, matematikçiler rastgele değer kavramını ele alırlar. Bazı durumlarda, görev buna izin verdiği için rastgele değerlerin kullanılması daha uygun olabilir. Rastgele bir değer, olay uzayını tanımlamak için biraz farklı bir yöntemdir. Bu durumda sonuç, bir veya daha fazla sayıdan oluşan net bir kümedir. Bunun bir vektör olduğunu söyleyebiliriz. Bu değerlendirme modeli, olasılık yoğunluğu kavramını ifade etmektedir. 

Bu kavramlar, bu konuyu incelerken daha fazla kullanılacaktır, bu nedenle şimdi bunları ele alalım. Olasılık yoğunluğu, tüm olay uzayını tanımlayan bir fonksiyondur. Bu fonksiyonun boyutu, bu olay uzayında her bir sonucu tanımlamak için gereken sayı sayısına tam olarak eşittir. Örneğin, bir atış poligonunda bir hedefe ateş etme problemini ele alırsak, hedef düz (iki boyutlu) olduğu için bu fonksiyonun boyutu ikiye eşit olacaktır. Bu durumda belirli bir sonuç X ve Y koordinatları ile karakterize edilecektir. Bu sayılar rastgele değişkenlerimizdir, bu nedenle şunu yazabiliriz:

• R = R(X, Y)
• R, (X,Y) koordinatlarına sahip bir noktaya isabet eden bir merminin olasılık yoğunluğudur

Bu fonksiyonun özellikleri, bu fonksiyonun tüm değişkenleri için eksi sonsuzdan artı sonsuza tam integralin bire eşit olmasını sağlar ve bu da yukarıdaki denklemi kanıtlar. Buradaki olasılıklar sadece fonksiyonun sunulduğu alanın integralleri tarafından belirlenir. Farklı olaylar parçalı entegre bölgelerden oluşabilir. Dolayısıyla, ihtiyaç duyduğumuz kadar çok olayı tanımlamak mümkündür, çünkü bunların sayısı sonsuzdur. Bu tanım, bu makale çerçevesinde yeterlidir.

Örtüşen olaylar hakkında biraz daha ayrıntı eklemek istiyorum. Bu tür olaylar da resmin bütününün genel olarak anlaşılması açısından çok önemlidir. Örtüşmeyen olaylarla başa çıkmanın, örtüşenlere kıyasla daha kolay olması gerektiği açıktır. Olasılık teorisi bazen olayların birleşimi veya bölünmesi ile ilgilenmek zorundadır. Ancak burada sadece bu dönüşümlerin sonucu olarak ortaya çıkan olasılıklarla ilgileniyoruz. Bu amaçla, olay toplamı ve çarpımı kavramlarının yanı sıra ters çevirme işlemini de kullanacağız. Bu işlemler matematikteki ile aynı anlama gelmemektedir. Dahası, sadece olasılıklarla çalışırlar. Birleşmiş olayların olasılıkları eklenemez, çünkü bu, kümenin bütünlüğünü ihlal eder. Genel olarak, kaynak olaylara uygulanan bu 3 işlem, kaynak olay parçalarından oluşturulabilecek tüm olası olayları tanımlayabilir. Örtüşen iki olay örneğini kullanarak, bunun düzlemde nasıl görünebileceğini gösterebilirim:

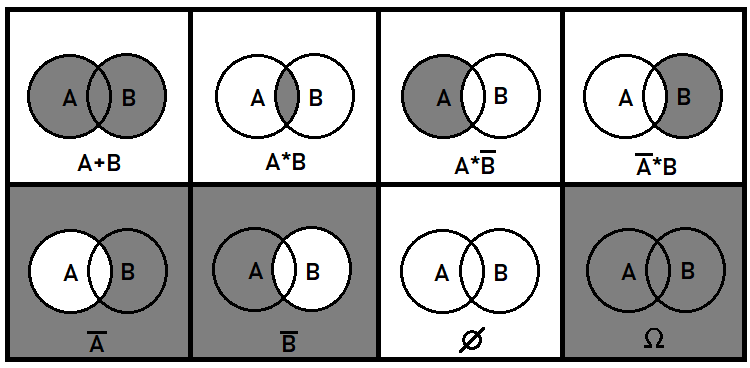
Ek cebirsel işlemler yukarıda sunulanlardan oluşabilir. Örneğin, boolean bölme işlemi yukarıdaki şekilde üçüncü ve dördüncü durumlara eşdeğerdir, çünkü bölme işlemi seçilen olayın tersi ile çarpmaya eşdeğerdir. Açıkça söylemek gerekirse, ilk iki olay, kaynak olay parçalarından oluşabilecek tüm olası olayları tanımlamak için yeterlidir. İkiden fazla örtüşen olayın olduğu durumlar çok daha zordur. Bu makalede sadece örtüşmeyen olaylarla ilgileneceğiz.

Piyasa matematiği temel olarak rastgele yürüyüş kavramına dayanır. Bu kavramı ele alacağız ve daha sonra bu olayları örüntülerin varlığıyla genelleştirmek mümkün olacaktır. Açılış fiyatından eşit uzaklıkta Zararı Durdur ve Kârı ala sahip ile bir pozisyon açtığımızı varsayalım. Burada makasları, komisyonları ve swapları dikkate almıyoruz. Dolayısıyla, ücretsiz şekilde pozisyonlar açarsak ve farklı yönlerde ve farklı grafik noktalarında rastgele işlem yaparsak, kâr/zarar oranı bire eşit olacaktır. Başka bir deyişle, sonsuz ticarette kârlı pozisyonların sayısı zararlı pozisyonların sayısına eşit olacaktır. Yukarıdakilere göre, ne kadar uzun süre işlem yaparsak yapalım kâr sıfır olacaktır. Tüm komisyonları, makasları ve swapları uygularsanız, nihai sonuç negatif olacaktır.

Bu sürecin matematiği her zaman zarara yol açtığı için rastgele yürüyüş anlamsız görünebilir. Ancak rastgele yürüyüş, farklı olayların olasılıklarının hesaplanmasına yardımcı olabilir. Bunlar, asimetrik durma seviyeleriyle kapatmayı veya grafiğin belirli bir fiyat aralığında geçeceği ortalama fiyatı içerebilir. Ayrıca, riskleri hesaplamada veya kârı maksimize etme ya da zararı minimize etme girişimlerinizde yardımcı olabilecek pozisyon ömrünü ve diğer faydalı değişkenleri de hesaplayabiliriz.

Olasılık ağaçları ve hipotezler

Frontal loblarınızı geliştirmek için çok faydalı bir örnek olay ağaçları veya olasılık ağaçlarıdır. Bu konu, tüm olasılık ağaçlarının temeli olan Bernoulli şemasından kaynaklanmaktadır. Bu şema, birbirini takip eden ve birbiriyle örtüşmeyen olay zincirlerini inceler. Ancak bundan önce, toplam olasılık formülünü ele alalım. Bu önemli yapıyı inceleyerek Bernoulli şemasına ve oradan da olasılık ağaçlarına geçebiliriz. Formül şu şekildedir:

• P(A) = Sum(0...i...n)[P(H[i])*P(A|H[i])] - A olayının olasılığı
• P(H[i]) - H[i] hipotezinin olasılığı
  
• P(A|H[i]) - A olayının H[i] hipotezi çerçevesinde gerçekleşme olasılığı

Olasılıklarla çalışırken bunları hipotez tarzında yazmanın daha iyi olduğunu söylemek isterim. Örneğin, P(H[k]|H[i]) girdisi şu anlama gelecektir:

1. H[i] uzayına göre hesaplanan H[k] olayının olasılığı

Bu şekilde, hangi olayın uzay olarak kabul edildiği ve hangi olayın iç içe geçtiği açıktır. Gerçek şu ki, her olay daha küçük bir olay uzayıdır, içinde başka olay da olabilir, bunlar da olay uzayı olarak hizmet edebilir ve bu böyle devam eder. Bu mantığa göre, P(H[i]) girdisi aşağıdaki gibi yazılabilir:

• P(H[i]|O) - çünkü bu olasılık O'ya göre tahmin edilir
  

Şimdi, arkasında ne olduğunu anlamak için toplam olasılık formülünü parçalara ayıralım. Formül ilk bakışta zor görünebilir, bu yüzden daha net hale getirelim. İlk olarak, formülü biraz farklı bir biçimde yeniden yazacağım:

• P(A) = (S[0]+...+S[i]+...+S[n])/O = S[0]/O+...+S[i]/O+...+S[n]/O = (S[0]/N[0])*(N[0]/O)+...+(S[i]/N[i])*(N[i]/O)+...+(S[n]/N[n])*(N[n]/O)
• S[i] - H[i] hipotezinin kesiştiği belirli segmentin alanı
• N[i] - tüm H[i] hipotezinin alanı (S[i] dahil)
• O - tüm sonuçlar veya tüm elipsin alanı

Pay ve paydayı N[i] değeriyle çarpmaktan ibaret olan küçük dönüşümlerden sonra, orijinal formülde mevcut olan olasılıkları görebiliriz:

• S[i]/N[i] ---> P(A|H[i])
• N[i]/O ---> P(H[i])

Grafiksel olarak aşağıdaki gibi görselleştirilebilir:

 

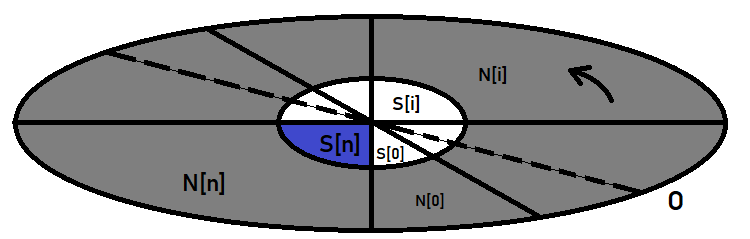
Dıştaki elips olay uzayıdır. Merkezdeki elips, olasılığını aradığımız olayımızdır. Bunun bir saat olduğunu varsayalım: elipsin çapını çizeriz, saat yönünün tersine döndürürüz ve elipsi hipotez olan parçalara keseriz. Bir hipotez, olaylar için yalnızca özel bir isimdir. Ancak, aslında bunlar aynı olaylardır ve olasılığını hesapladığımız olaydan hiçbir farkları yoktur.

Bu formülün Bernoulli şemasının oluşturulmasında yardımcı olacak özel bir durumu vardır. Merkezi elipsin tamamen bu hipotezlerden birinin içerisinde olduğunu düşünelim. Daha sonra, bu toplamın hipotezlerin geri kalanıyla ilgili tüm terimlerinin otomatik olarak sıfırlandığı ortaya çıkar, çünkü bu hipotezler içerisinde A olayının gerçekleşme olasılığı imkansızdır veya sıfıra eşittir, bu da sonuçta bu terimleri sıfırlar. Sonuç olarak, şu ortaya çıkar:

• P(A) = P(H)*P(A|H)
• H - seçilen olayın tam olarak içinde yer aldığı hipotezin olasılığı

Ayrıca, A olayının da bir hipotez olarak adlandırıldığını varsayarsak ne olur? Neden olmasın? Bir hipotez bir olaydır, dolayısıyla her olay bir hipotezdir. Şimdi, A'nın içerisinde yer alan başka bir B olayı olduğunu varsayalım. O zaman A, B'ye göre bir hipotezdir ve önceki formül bu iki olay için geçerlidir:

• P(B) = P(A)*P(B|A) = P(H)*P(A|H)*P(B|A)

P(A) yerine önceki oranı ekleyelim - herhangi bir sayıda iç içe geçmiş hipotez veya olay için genel bir formül oluşturmada belirli bir örüntü görebilirsiniz. Bunun amacı nedir? Bu, biraz sonra ele alacağımız Bernoulli formülünün doğrudan prototipidir. Şimdi, göz önünde bulundurulması gereken ilginç bir gerçek daha var.

Fraktallar hakkında

Yukarıdaki formüle göre, P(A)+P(B) = 1 ise, bu bir kolektif kapsamlı olaylar kümesidir. Bu, bir tam grubun iç içe geçmiş iki rastgele hipotez zincirinden oluşabileceği anlamına gelir. Ancak bu hipotezler birbiriyle örtüşebilir. Tüm olası iç içe geçmiş hipotezlerin diğer zincirlerin hipotezleriyle örtüşmemesini istersek, otomatik olarak tüm zincirler bu olay uzayındaki tüm zincirlerle örtüşmeyecektir. Bunun grafiksel gösterimi oldukça ilginç bir örüntüdür:

Bu örüntüye fraktal denir, çünkü böyle bir yapının sonu yoktur; sonsuza kadar inşa edilebilir. Yukarıdaki şekilde yapı sadece 3 seviye derinliğindedir. Mavi dikdörtgenler ayrı bir olasılıklar zincirinin sonunu temsil etmektedir. Tüm bu zincirlerin olasılıklarını toplarsak, bunlar bir kolektif kapsamlı olaylar kümesi oluşturacaktır.

Bu tür fraktallar kombinasyonlarla iyi bir şekilde tanımlanabilir. Kombinasyonlar faktöriyel kavramına dayanır. Faktöriyel ve kombinasyon arasında bir yerde olan başka bir kavram daha vardır, permütasyon. Permütasyon formülü faktöriyel formülünden türetilir ve kombinasyon kavramı da permütasyon formülünden türetilir. İşte ilgili formüller:

• n! - n sayısının faktöriyeli
• P(n, k) = n!/(n-k)! - N elemandan K elemana permütasyonlar
• С(n, k) = n!/(k!*(n-k)!) - N elemandan K elemana kombinasyonlar

Bir faktöriyel, 1 ile başlayıp n ile biten tüm doğal sayıların çarpımıdır. Ayrıca, "0! = 1". Yani, sıfırın faktöriyeli bire eşittir. Bu durumda, bu sadece kuralın bir istisnasıdır, ancak bu istisnanın hesaplamalara müdahale edeceği veya algoritmaları karmaşıklaştıracağı tek bir durum görmedim.

Permütasyonlar biraz daha karmaşıktır. Bir deste kartınız olduğunu ve bu destede belirli sayıda kart olduğunu düşünün. Basit bir deney yapalım: desteyi karıştırın ve desteden tamamen keyfi bir şekilde birkaç kart alın, bunları desteden çıkarıldıkları sırayla masaya koyun. Dolayısıyla, permütasyonlar bu deneyin tüm olası sonuçlarının sayısıdır ve kartların sırası da belirli bir sonucun benzersiz bir tanımlayıcısı olarak kabul edilir. Bu tür bir permütasyon istenen herhangi bir unsur için geçerlidir.

İlk kart desteden n farklı şekilde alınabilir, ikincisi ise ilk kart artık destede olmadığı için "n-1" şekilde alınabilir. Ve böylece "n-k-1" kartına kadar devam eder. Tüm olası permütasyonların sayısını elde etmek için, "n-k-1" ile "n" arasındaki tüm sayıları çarpmamız gerekir. Bu prosedür bir faktöriyele benzemektedir. Eğer "n!" alır ve "n-k" çarpanlarına bölersek, tam olarak "(n-k)!"e eşit olan orijinal çarpımı elde ederiz. Permütasyon formülünü bu şekilde elde ederiz.

Kombinasyon formülü biraz daha karmaşıktır, ancak çıkarılması da çok kolaydır. Tüm olası permütasyonlara sahibiz, ancak burada elemanların sırası önemli değil - sadece bu setteki kartlar önemli. Şimdi, her biri farklı bir kart setine sahip olan bu tür durumların sayısını bulmamız gerekiyor. Aslında, her permütasyon zaten bu benzersiz kümelerden birini içerir, ancak hepsine ihtiyacımız yoktur. Mantığı değiştirelim ve olası tüm kombinasyonlardan tüm permütasyonları elde etmeye çalışalım: bir kombinasyonu alırsak, içindeki öğeleri nasıl yeniden düzenlersek düzenleyelim, benzersiz olacakları ortaya çıkar. Ayrıca, tüm benzersiz kombinasyonları alır ve içlerindeki tüm olası permütasyonları üretirsek, aşağıdaki ifadeyi elde ederiz:

• P(n, k) = C(n, k)*P(k, k)

Bir kombinasyon içindeki tüm olası benzersiz permütasyonların sayısı "P(k, k)"ya eşittir, çünkü bu "k" varyant için tüm olası permütasyonları "k" varyanttan elde etmemiz gerekir. Denklemin her iki kısmını da "P(k, k)" ile bölerek gerekli kombinasyon formülünü elde ederiz:

• C(n, k) = P(n, k)/P(k, k) = n!/(k!*(n-k)!)
  

Hem permütasyonlar hem de kombinasyonlar çeşitli olasılık teorisi problemlerinde yaygın olarak kullanılmaktadır. Pratik uygulamalar söz konusu olduğunda, bizim için son derece yararlı olan kombinasyonlardır. Kombinasyonlar, fraktal fonksiyonlarının oluşturulmasında çeşitli amaçlar için kullanılır. Belki de bunlara tekrarlayan fonksiyonlar demek daha doğru olur, ancak bazı nedenlerden dolayı bu tür fonksiyonlara fraktal fonksiyonları diyorum (muhtemelen gerçekten fraktal oldukları için, yani sadece bir özyineleme değil, tüm bir çağrı ağacı olduğu için).

Bernoulli şeması

Bu tür fraktal fonksiyonlarını incelemeye geçmeden önce, iyi bilinen Bernoulli formülünü ele alalım. Birkaç kez tekrarlamamız gereken aynı deneyler zincirine sahip olduğumuzu varsayalım. Deney, belirli bir olasılıkla bir olayın ortaya çıkması veya çıkmaması ile sonuçlanmalıdır. Ayrıca, "n" deneyden oluşan bir zincirde olayımızın tam olarak "k" kez ortaya çıkma olasılığını bulmak istediğimizi varsayalım. Bernoulli formülü bu soruya cevap verebilir:

• P = C(n, k)*Pow(p, k)*Pow(q, n-k) - Bernoulli formülü
  
• p - tek bir deney sonucunda olayın gerçekleşme olasılığı
• q = 1-p - deney sonucunda olayın gerçekleşmeme olasılığı

Olasılık zincirleri için daha önce türetilen formülü hatırlıyor musunuz? Bunu rastgele büyük bir zincir uzunluğu için genişletelim:

• P(n) = P(H[1]|O)*P(H[2]|H[1])*P(H[3]|H[2])*...*P(H[k]|H[k-1])*...*P(H[n]|H[n-1])
• n - zincirdeki segment sayısı
• O - tüm sonuçlar kümesi; H[0] olarak gösterilebilir

Bu formül, tam olarak gerekli hipotezler zincirinin gerçekleşme olasılığını hesaplar. Formül görsel olarak aşağıdaki gibi gösterilebilir:

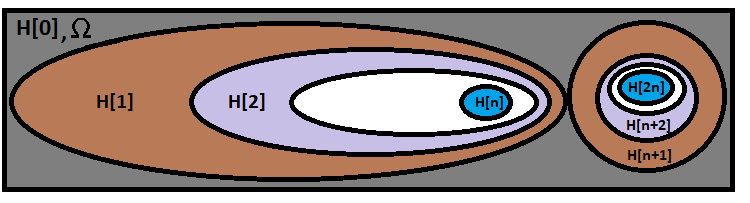
Formülümüz ilk ve en büyük elipsin içerisinde yer alırken, sağdaki başka bir zincir bizim zincirimizle örtüşmüyor ve farklı bir kombinasyondan başka bir dalı sembolize ediyor. Formülümüzde kombinasyonları hesaplamak için ne kadar varyant varsa o kadar dal vardır. Bu yüzden kombinasyonları kombinasyon hesaplama varyantları ile karıştırmayın. Kombinasyonların hesaplanması için varyant sayısı şuna eşittir:

• n+1 ("0" başarılı sonuç kombinasyonları da sayıldığı için)
• n - deney zincirindeki bağımsız testlerin sayısı

Şimdi tüm bu hipotezlerin olasılıklarının "p" ya da "q"ya eşit olduğunu düşünelim. Daha sonra formül basitleştirilir:

• P(n) = Pow(p, k)*Pow(q, n-k)
• k - çarpımda "p"ye eşit kaç çarpan var
• n-k - çarpımda "q"ya eşit kaç çarpan var

Bernoulli formülüne zaten benziyor, ancak kombinasyondan yoksun. Dikkatlice düşünürseniz, benzer olasılığa sahip zincirlerin varyantlarının ve "k" ve "n-k" miktarının tam olarak "C(n, k)"ya eşit olduğu anlaşılır. Tüm olasılık zincirleri örtüşmediğinden, bu zincirlerden birini elde etme olasılığı, tüm bu zincirlerin olasılıklarının toplamıdır. Tüm bu olasılıklar aynı olduğundan, Bernoulli formülünü elde etmek için bir zincirin olasılığını bunların sayısıyla çarpabiliriz:

• P = C(n, k)*Pow(p, k)*Pow(q, n-k)

Bu formül, örneğin, kesin olarak sabit bir kombinasyonun değil, bir olayın k ve daha fazla kez, k ve daha az kez ve tüm benzer kombinasyonlarda meydana gelme olasılığını bulmamız gerektiğinde daha da genişletilebilir. Bu durumda, gerekli tüm kombinasyonların olasılıklarının toplamı olacaktır. Örneğin, olayın k kereden fazla gerçekleşme olasılığı aşağıdaki şekilde hesaplanır:

• P = Summ(k+1...i...n)[C(n, i)*Pow(p, i)*Pow(q, n-i)]

Şunu anlamak önemlidir:

• P = Summ(0...i...n)[C(n, i)*Pow(p, i)*Pow(q, n-i)] = 1

Başka bir deyişle, tüm olası zincirler bir kolektif kapsamlı olaylar kümesi oluşturur. Bir diğer önemli denklem de şudur:

• Summ(0...i...n)[C(n, i)] = Pow(2, n)
  

Olasılık zincirinin her bir parçasının yalnızca iki durumu olduğu düşünüldüğünde bu mantıklıdır: "olay gerçekleşti" ve "olay gerçekleşmedi". Olayın gerçekleşmediği durum da başka bir olayın gerçekleştiğini ima eden bir olaydır.

Kombinasyonların ilginç bir özelliği daha vardır:

• C(n, k) = C(n, n-k)
  

Bu değer şu şekilde elde edilir: "C(n, n-k)" hesaplanır ve "C(n, k)" ile karşılaştırılır. Bazı küçük dönüşümlerden sonra, her iki ifadenin de aynı olduğunu görebiliriz. Yukarıdaki tüm ifadeleri kontrol etmek için MathCad 15 tabanlı küçük bir program oluşturdum:

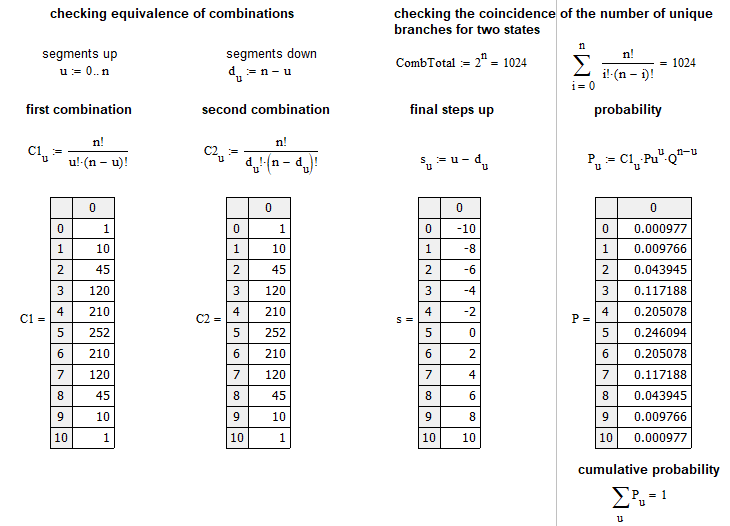
Bu örnek piyasaya yakındır. Piyasanın n adımda u adım yukarı hareket etme olasılığını hesaplar. Bir adım, bir önceki adıma göre belirli sayıda puan yukarı veya aşağı fiyat hareketidir. Her bir "u" için olasılıkların grafiksel dizisi aşağıdaki gibi gösterilebilir:

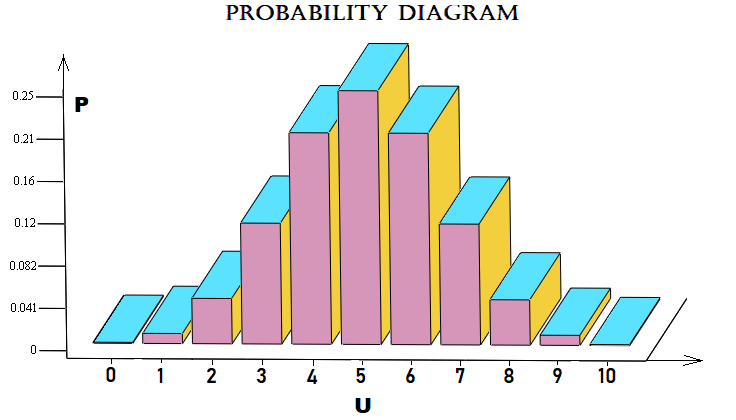
Basit olması için 10 adımlı bir Bernoulli şeması kullandım. Test edebilmeniz için dosya aşağıda eklenmiştir. Bu şemayı mutlaka fiyatlandırmaya uygulamanız gerekmez. Emirlere veya başka herhangi bir şeye de uygulanabilir.

İlk fraktalın oluşturulması

Zararı Durdur ve Kârı Al seviyeleri ile ilgili problemlere özel dikkat gösterilmelidir. Zararı Durdur ve Kârı Al değerlerini puan cinsinden (mevcut fiyattan uzaklık) bildiğimizde, bir işlemin Zararı Durdur veya Kârı Al tarafından kapatılma olasılığını bir şekilde hesaplamalıyız. Tüm bu hususlar doğrudan fiyatlandırma mekanizmalarına bağlı olduğundan, bu değer artık açılış fiyat olmasa bile herhangi bir noktada hesaplanabilir. Bu örnekte, fraktalları kullanarak formülün ispatını göstermek istiyorum. Rastgele yürüyüş durumunda bu olasılık aşağıdaki şekilde hesaplanabilir:

• P(TP) = SL/(TP+SL) - Kârı Al gerçekleşme olasılığı
• P(SL) = TP/(TP+SL) - Zararı Durdur gerçekleşme olasılığı
• SL - zararı durdurmak için puan cinsinden mesafe
  
• TP - kârı almak için puan cinsinden mesafe

Bu iki olasılık bir kolektif kapsamlı olaylar kümesi oluşturur:

• P(TP)+P(SL) = 1
  

Bu formüle göre, rastgele ticaret için, makas, komisyon ve swapı hariç tutarsak, bu tür stratejilerin matematik beklentisi sıfır olacaktır:

• M = P(TP)*TP - P(SL)*SL = 0

Bu, sabit bir durma seviyesi belirlediğimiz en basit durumdur. Ancak bunu kesinlikle herhangi bir stratejiye genellemek mümkündür. Şimdi, aynı MathCad 15'i kullanarak formülü kanıtlayalım. Bu programla uzun süredir çalışıyorum. Programlama kullanarak bile hemen hemen her karmaşıklık düzeyinde hesaplamalar üretebilir. Bu örnekte, yukarıdaki formülleri kanıtlamanın yanı sıra, bir fraktal formülü oluşturmanın ilk örneğini göreceğiz. Fiyat hareketi sürecinin taslağını çizerek başlayalım. Burada sürekli fonksiyonları kullanamayız, sadece ayrık olanları kullanabiliriz. Bunun için koşullu emrimizi alalım ve yukarı ve aşağı durma seviyesi mesafelerini hesaplayalım, ardından bu segmentleri eşit adımlarla parçalara ayıralım, böylece her adım tam sayı adım içerir. Fiyatın bu adımlarla hareket ettiğini düşünelim. Adımlar eşit olduğundan, iki yönden herhangi birinde adım atma olasılığı 0.5'tir. Uygun fraktalın uygulanması için grafiksel bir gösterime ihtiyacımız vardır:

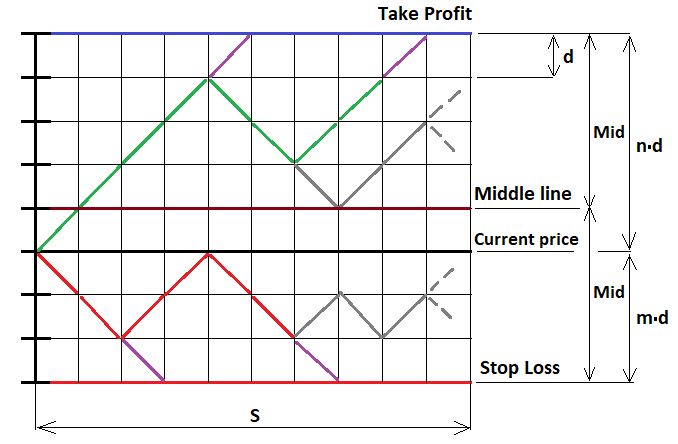
Bu problemi çözmek için üç olası fraktal devamlılık durumunu ele alalım:

1. Orta çizginin üzerindeyiz (U > MiddleLine)
2. Orta çizginin altındayız (U < MiddleLine)
3. Orta çizgi seviyesindeyiz (U = MiddleLine)

"U", açılış fiyatına göre "u-d" yukarı adımların toplam sayısıdır. Fraktal oluşturmaya devam edeceğimiz nokta fiyatın altındaysa, U fonksiyona uygun olarak negatif değerler alır. Eğer orta çizgideysek, çizgiyi geçme korkusu olmadan atabileceğimiz adım sayısı Mid'den bir eksiktir. Ancak yapıya geçmeden önce, fraktal yapısını fiyat veya emirlerin yapabileceği adım sayısıyla sınırlamalıyız. Adım sayısı gerekli sayıyı aşarsa, daha fazla yapımını durdurmalıyız. Aksi takdirde, içinden çıkmanın imkansız olacağı sonsuz bir özyineleme elde ederiz. Hesaplama süresi sonsuza eşit olacaktır.

Şekilde birkaç mor adım çizdim - bu noktalarda olasılıkları bir araya getiriyoruz ve bunları ortak bir değişkende topluyoruz. Bundan sonra, zincirin hangi sınıra dokunduğuna bağlı olarak zincirimizi yukarı veya aşağı çevirmemiz gerekir, böylece yeni iç içe fraktal seviyeleri oluşturmak için daha fazla hareket etmeye devam edebilir. Diğer noktalarda, Bernoulli şemasına dayalı olarak tüm fraktal seviyelerini serbestçe oluşturabiliriz.

Bernoulli şemasına dayalı bir ağaç oluşturmak mümkün olduğunda, öncelikle tüm adımların sadece yukarı veya sadece aşağı olduğu uç durumları dikkate alarak yapabileceğimiz adım sayısını belirlemeliyiz. Her üç durum için de değer eşittir:

• (n-1)-U - zincirimiz zaten orta çizginin üzerindeyken (U'daki bir artış üst sınıra olan mesafenin azalmasına neden olduğundan)
• (m-1)+U - zincirimiz zaten orta çizginin altındayken (U'daki bir azalma alt sınıra olan mesafenin azalmasına neden olduğundan)
• (floor(Mid)-1) - zincirimiz tam olarak orta çizgideyken
• n - üst segmentlerin sayısı
• m - alt segmentlerin sayısı
• floor - fonksiyon ondalıklı kısmı atar (bu gerekli olmayabilir)

Öncelikle iki yardımcı değeri hesaplamamız gerekiyor:

• Mid = (m+n)/2 - aralık genişliğinin yarısı (adım cinsinden)
• Mid = (m+n)/2-m - orta çizgi için "U" değeri (adım cinsinden)

Bu değerler daha sonra fraktal dallanma mantığını tanımlamak için kullanılacaktır. Şimdilik, sadece "n >= m" olduğu durumlar için fraktal oluşturacağız. Ancak bu veriler bir fraktal oluşturmak için yeterli değildir. Daha derin fraktal seviyeleri inşa edebilmek için, Bernoulli şemasındaki her yeni kombinasyon için "U"yu yeniden tanımlamak ve yeni bir fraktal seviyesine aktarmak gerekir. Buna ek olarak, gerçekleştirilen adımların sayısını doğru bir şekilde artırmak ve ayrıca onları doğru bir şekilde ilerletmek gerekir. Benzer şekilde, bir sonraki fraktal seviyesinin çarpanlarını kullanarak tüm zincirin olasılığını elde etmemiz ve bu süreç gerekli sınırın başarılı bir şekilde geçilmesiyle sona erene kadar ara zincirin olasılığını bir sonraki seviyeye geçirmemiz gerekir. Aşağıdaki görüntü bu üç durumu açıklamaktadır:

  

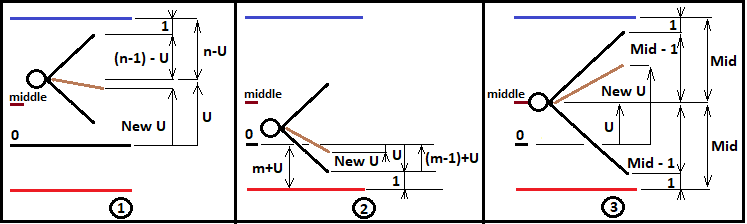
Bu diyagrama göre, şimdi "NewU" değerlerinin ve diğer yardımcı değerlerin sunulan her durum için neye eşit olacağını yazabiliriz. Üst sınırı geçme olasılığını hesaplamak için bir fraktal inşa etme örneğini ele alalım:

1. durum için:

Üstteki şekle bir göz atalım ve orada neler olduğunu matematiksel olarak açıklayalım. Bu şekil MathCad 15'teki programımdan bir özeti göstermektedir. Programın tüm kodu aşağıda eklenmiştir. Burada fraktalın temelini oluşturan en önemli detayları veriyorum. İlk dikdörtgen bir döngü içindedir ve tüm olası kombinasyonları tanımlamak için "i" ile yinelenir. Bu mantık MetaEditor IDE'de tekrarlanabilir. Diyagramdaki ilk çizimle başlayalım. "NewU"yu tanımlamak için öncelikle bazı temel formülleri tanımlamamız gerekiyor:

• (n-1)-U = f - gelecekteki kombinasyon ağacının adım sayısı (mesafe, fraktal aralığının en yakın sınırına olan mesafe ile belirlenir)
• u+d = f - aynı değer, ancak yükselen ve düşen segmentlerin sayısı cinsinden ifade edilir
• s = u-d - düşen ve yükselen segmentler cinsinden ifade edilen nihai adım sayısı
• u = i - bunun nedeni programımın "i" ile yineleme kullanmasıdır (hatırlanmalıdır)

Gerekli tüm değerleri hesaplamak için "s"yi "U" ve "i" ile ifade etmemiz gerekir. Bunun için "d" değişkenini hariç tutmamız gerekir. Önce bunu ifade edelim ve ardından "s" için ifadenin içine yerleştirelim:

1. d = f-u = f-i = (n-1)-U-i
2. s = i-(n-1)+U+i = -(n-1)+2*i+U

Ardından, bulunan "s"yi kullanarak "NewU"yu ve bir sonraki fraktal seviyesine aktarılacak tüm değerleri buluruz:

• NewU = s+U = -(n-1)+2*i+2*U - bir sonraki fraktal seviyesine geçecek yeni "U"
• NewP = P*C(f, i)*Pow(p, i)*Pow(1-p, f-i) = P*C((n-1)-U, i)*Pow(p, i)*Pow(1-p, (n-1)-U-i) - bir sonraki fraktal seviyesine geçecek yeni "P" zinciri olasılığımız (zincirin yeni segmentinin olasılığı ile çarpılarak elde edilir)
• NewS = S+f = S+(n-1)-U - bir sonraki fraktal seviyesine geçecek yeni "S"

Şimdi, alttaki dikdörtgene göz atalım. Burada, adım zincirinin aralığın üst sınırına ulaştığı durumları ele alıyoruz. Burada iki durum ele alınmalıdır:

1. Sınırla kesişen zincirin olasılığını elde etme (altı kırmızı ile çizili)
2. Bir sonraki fraktal seviyesine aktaracağımız yeni değerleri artırmak için benzer eylemler

Sadece iki olası seçenek olduğundan bu durum çok daha basittir:

1. Sınıra dokunma
2. Sınırdan geri dönüş

Bu eylemler Bernoulli şemasına ihtiyaç duymaz, çünkü her durum yalnızca bir adım anlamına gelir. Geri dönüş olasılığı ayrıca "(1-p)" ile çarpılır, çünkü kesişme olasılığı "p"dir ve bu iki olay, önceki hesaplamalardan da anlaşılacağı üzere, bir kolektif kapsamlı küme oluşturmalıdır. Adımlar 1 artırılır ve "U" da 1 azaltılır, çünkü bu aşağı inen bir yansımadır. Şimdi bu durumu doğru bir şekilde inşa etmek için her şeye sahibiz. Bu kurallar, tamamen farklı durumlar için ihtiyaç duyduğumuz ana fraktalları oluşturmak için aynı olacaktır.

2. durum için:

Hesaplama bu durum için neredeyse benzerdir. Tek fark "f"nin farklı bir değer almasıdır:

• (m-1)+U = f

Yine, önceki durumdaki aynı formülleri kullanarak "s"yi "U" ve "i" ile ifade edelim:

1. d = f-u = f-i = (m-1)+U-i
2. s = i-(m-1)-U+i = -(m-1)+2*i-U

Benzer şekilde, bir sonraki fraktal seviyesine geçecek diğer tüm değerleri buluyoruz:

• NewU = s + U =-( m - 1 ) + 2*i  - bir sonraki fraktal seviyesine geçecek yeni "U"
• NewP =P*C(f, i)*Pow(p, i)*Pow(1-p, f-i) = P*C((m-1)+U, i)*Pow(p, i)*Pow(1-p, (m-1)+U-i) - bir sonraki fraktal seviyesine geçecek yeni "P" zinciri olasılığımız
• NewS = S+f = S+(m-1)+U - bir sonraki fraktal seviyesine geçecek yeni "S"

Alttaki dikdörtgen önceki durumla neredeyse aynıdır, ancak "U"yu 1 artırıyoruz, çünkü yansıma artıyor ve dolayısıyla "U" da artıyor. Bu durumda olasılıklar toplanmamaktadır, çünkü bu fraktalda alt sınırla kesişme ile ilgilenmiyoruz. Şimdi, işte zincirin aralığın orta çizgisinde meydana geldiği son durum.

3. durum için:

"f"yi tanımlayalım:

• floor(Mid)-1 = f

"s"yi bulalım:

1. d = f-i = floor(Mid)-1-i
2. s = i-d = -(floor(Mid)-1)+2*i

Son olarak, bir sonraki fraktal seviyesine geçecek değerleri bulalım:

• NewU = s+U = -(floor(Mid)-1)+2*i+U
  
• NewP = P*C(f, i)*Pow(p, i)*Pow(1-p, f-i) = P*C(floor(Mid)-1, i)*Pow(p, i)*Pow(1-p, floor(Mid)-1-i) - bir sonraki fraktal seviyesine geçecek yeni "P" zinciri olasılığımız
• NewS = S+f = S+(floor(Mid)-1) - bir sonraki fraktal seviyesine geçecek yeni "S"

Bu durumun ayırt edici bir özelliği, bloğun olasılıkları toplamamasıdır, çünkü olasılıklar yalnızca olasılık zincirlerinin daha fazla yayılabilmeleri için zincire geri yansıtıldığı "U" sınır değerlerinde toplanabilir. Üst sınırı geçme olasılığını hesaplamak için bir fraktal oluşturulması aynı olacaktır, ancak olasılıklar ilk durumda değil, ikinci durumda sayılacaktır.

Bu tür fraktalların inşasındaki ilginç bir özellik, bu tür fonksiyonlarda Bernoulli formülünün zorunlu olarak bulunmasıdır. Kombinasyonlar pembe renkle vurgulanmış ve olasılıkların çarpımları sarı renkle gösterilmiştir. Bu iki çarpan birlikte Bernoulli formülünü oluşturur.

Şimdi, aynı anda iki şeyi kontrol edelim: tüm fraktalın yapısının doğruluğu ve beklenen getirinin yalnızca tahmin yeteneğine bağlı olduğu varsayımı. Adımlar puanlar ve işlemler olarak sunulabilir. İkinci durumda puan, lota ve tik büyüklüğüne bağlı olan uygun orantılılık katsayısı ile çarpılmalıdır. Burada puan kullanacağız - bu temsil evrenseldir:

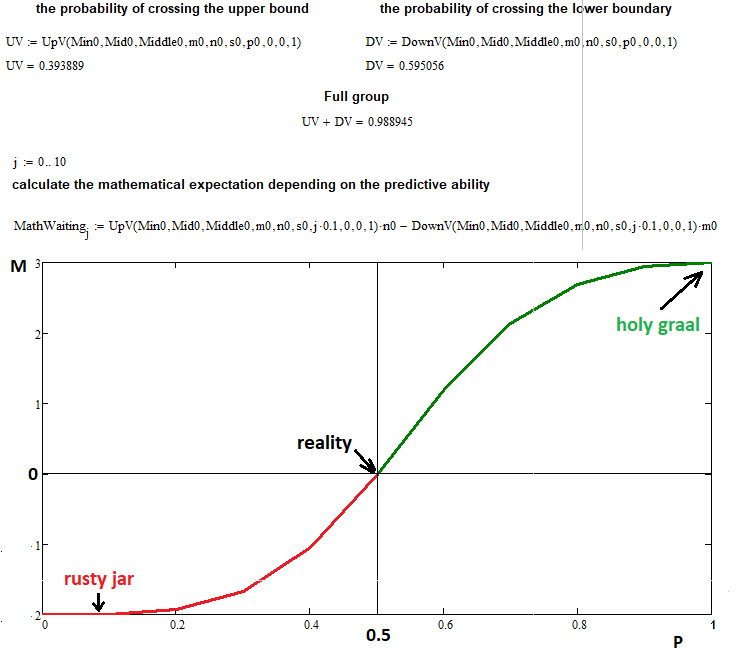
Bu örnekte, matematiksel beklentiye karşı yukarı adım olasılığını çizmek için aşağıdaki girdi verilerini kullandım:

• n = 3 - üst segmentlerin sayısı
• m = 2 - alt segmentlerin sayısı
• s = 22 - fraktal fonksiyonunun zincirleme reaksiyonu için izin verilen adım sayısı (bu değeri artırırsanız, bilgisayarda ekstra yük oluşturacaktır, bu nedenle bu adım sayısı oldukça yeterlidir)
• 0 ... 0.1 ... 0.2 ...... 1.0 - yukarı adım olasılıkları aralığının 0.1'lik adımla 10 parçaya bölünmesi

Gördüğünüz gibi, 0.5 olasılığı için işlemlerimize ilişkin matematiksel beklenti, daha önce formül tarafından öngörüldüğü gibi sıfıra eşittir. 0 ve 1 uç noktalarında, fonksiyon değeri "n" ve "-m" değerlerine yönelir, bu da varsayımlarımızı doğrular. Fraktal, bir dezavantajı ortaya çıkarmasına rağmen görevini başarıyla tamamlamıştır: hesaplama süresinde ve karmaşıklıkta büyük bir artış. Ancak, benzer görevler için birkaç saat hatta bir gün beklemek oldukça kabul edilebilir.

Bu fraktal yalnızca n >= m olduğunda, yani üst sınıra kadar olan mesafenin alt sınıra kadar olan mesafeden daha büyük olduğu durumlarda çalışır, ancak fraktalda bunu sağlamaya gerek yoktur. Bu yapı yansıtılabilir: n < m ise, n yerine m'yi ve m yerine n'yi geçirerek fraktalı hesaplayabiliriz. Ardından olasılıkları değiştiririz ve istenen sonucu elde ederiz. Bu tür fraktallar sadece formülleri kanıtlamak için değil, aynı zamanda tersine bir işlem için de kullanılabilir. Bazı formüller sadece fraktalların kullanılması sonucunda elde edilebilir.

Özet

Bu makalede aşağıdaki çok önemli sonuçlara varıldığını düşünüyorum:

• Programlama ile birleştirilen olasılık teorisi, piyasa süreçlerinin birçoğunu tanımlamak için teorik bir temel sağlayabilir.
• Olasılık teorisinin ana hükümleriyle birleştirilen fraktallar en zor sorulara cevap verebilir.
• Oldukça karmaşık bir fraktal oluşturmanın bir örneğini gördük.
• Tüm teori, MathCad 15 ortamında programlama kullanılarak pratikte test edilmiştir.
• Makale, Bernoulli şemasının iki adımlı durumlara sahip herhangi bir fraktal oluşturmak için olanaklar sağladığını kanıtlamıştır.

Sonuç

Umarım bu makale sayesinde ticaretiniz için pratikte kullanabileceğiniz yeni şeyler bulabilirsiniz. Bu makale üzerinde çalışırken, sizi başka bir zor göreve - fraktal olasılık zincirlerini kullanarak piyasa süreçlerini tanımlamaya - hazırlamak için ayrık matematiğin ve olasılık teorisinin tüm gücünü aktarmaya çalıştım. Olasılık teorisinin tüm ana hükümlerini, pratik ticaret için karmaşık görevleri çözmede daha fazla yardımcı olabilecek tek bir materyalde birleştirmeye çalıştım. Ayrıca, alakasız tüm ayrıntıları ayıklamaya çalıştım. Bir sonraki makale fraktalların pratik uygulamalarına ilişkin yeni örnekler ve diğer önemli sorulara yanıtlar sunacaktır.