Implementation of the Augmented Dickey Fuller test in MQL5

Introduction

The Augmented Dickey-Fuller (ADF) test is a common procedure used to assess whether a time series is stationary or not.  Although, it is well known that financial time series are inherently non-stationary. Many statistical methods that benefit from stationarity usually require that non-stationary datasets be transformed in some way before being analyzed. The ADF  test can be used to evaluate the efficacy of these tranformations in inducing stationarity. Alternatively, evaluating the cointegration of series also makes use of tests for stationarity. Usefull in the development of trading strategies that exploit discrepancies in pricing of related financial instruments. In this article we will present the implementation of the ADF test in pure MQL5 and demonstrate its application by using it to identify cointegrated symbols in MetaTrader 5.

Understanding the ADF Test

Simply put an ADF test is a hypothesis test, that allows us to determine if a specific characteristic of the observed data is statistically significant. In this instance the characteristic being acertained is the stationarity of a series.  A statistical hypothesis is an assumption made about a data set that is represented by a sample. We can only know the real truth by working with the entire data set. Which is usually not possible for one reason or another. So a sample of a data set is tested to posit an assumption of the entire data set. The important point to remember here is that the truth of a statistical hypothesis is never known with certainty when working with samples. What we get is whether an assumption is likely true or false.

In an ADF test we consider two scenarios:

• The Null hypothesis that a unit root is present in the time series.

• The Alternative hypothesis that the times series does not exhibit a unit root.

In time series analysis a unit root is a special characteristic of a sequential data set. Imagine a man walking down a street with their dog. The man will likely walk in a fairly straight line towards his destination. Whilst the dog will often wander off, to sniff at something or chase some critter that has caught its attention. But ultimately it will follow its owner. If the path of the dog is plotted we may observe some type of oscillation. Where the dog wanders off, but eventually reverts back to the expected general direction being followed by the man.

An arbitrary point on the dog's path represents the value of a variable at a specific time. If we evaluate these values, its likely they will stay with in a certain range around a central tendency. The statistical properties donot change significantly over time. Such a series will not have a unit root. Now imagine if the man was walking his untrained dog on the same street. The dog will likely run off and never come back to the owner. The values associated with the path taken by this dog wil vary unpredictably. Such a series will have a unit root.

The notion of a unit root comes from the characteristic equation of a stochastic process. A stochastic process is a sequence of variables indexed by time, describing a system that evolves randomly. The characterisitc equation of a stochastic process is an equation that captures the system's properties. The unit root is a solution of the characteristic equation that equals 1. If a process has a unit root, it means that the shocks or random effects have a persistent effect on the process. Such a system is modelled by random effects and  lagged values. Meaning that it is autoregressive in nature.

Therefore, the ADF test uses a regression model to test for a unit root. The most common form of the model is given by the equation below.

Where:

• " Y " The first difference of the time series
  

•  "a"  A constant term

•  "b" The coefficient of the lagged level of the time series
  

•  "x" The coefficient of the time trend (t)

•  "V" Coefficients of lagged first differences
  

•  "E" The error term

The test focuses on the coefficient "b". If "b" = 0, there is a unit root otherwise if  "b" < 0, the time series is stationary. The ADF statistic is calculated based on the estimated value of "b" and its standard error. It's compared to critical values from a Dickey-Fuller distribution. If the ADF statistic is more negative than the critical value at a specific significance level, the null hypothesis of a unit root is rejected. Meaning that the series is stationary.

Implementation

In order to ensure that our implementation is accurate we will use an existing implementation of the ADF test in Python as a reference. In the 'statsmodels' Python package, the `adfuller` function is used to perform an ADF test.

adfuller(x, maxlag: 'int | None' = None, regression='c', autolag='AIC', store=False, regresults=False)

The function first estimates the parameters of an autoregressive model of the input series using ordinary least squares. A test statistic is computed based on the estimated parameters. Which is used to calculate a p-value. Three critical values are drawn from a distribution table which represent confidence levels. Finally, the test statistic can be compared against anyone of these values to determine  whether a series is stationary or not.

Based on this overview, there are three important components we have to implement. First is the ordinary least squares regression model. Probably the most important component, as any errors here will propagate to other stages of the test. This will be used to determine the most appropriate autoregressive model of the series being analyzed. Besides the model parameters we also need to calculate various properties of a model, such as its Akaike information criteria and Bayesian information criteria.

The second component relates to the calculation of the p-value. The p-value is determined by the a test statistic derived from the t-statistic  of the optimal autoregressive model. A t-statistic is a measure used to determine if there is a significant difference between the means of two groups. It is calculated by taking the difference between the sample means and dividing it by the standard error of the difference. In this context the t-statistic is computed by dividing the model's parameters by the model's standard error. The method employed to calculate the p-value was proposed by J.G. MacKinnon and is therefore called MacKinnon's approximate p-value method. It provides an approximation for the p-value associated with critical values from statistical tests.

The last component needed to complete the ADF test is the computation of the critical values. These values are derived from approximations given in an academic paper written by MacKinnon.

//+------------------------------------------------------------------+
//| Ordinary least squares class                                     |
//+------------------------------------------------------------------+
class OLS
  {
private:
   matrix m_exog,               //design matrix
          m_pinv,               //pseudo-inverse of matrix
          m_cov_params,         //covariance of matrix
          m_m_error,            //error matrix
          m_norm_cov_params;    //normalized covariance matrix
   vector m_endog,              //dependent variables
          m_weights,            //weights
          m_singularvalues,     //singular values of solution
          m_params,             //coefficients of regression model(solution)
          m_tvalues,            //test statistics of model
          m_bse,                //standard errors of model
          m_resid;              //residuals of model
   ulong  m_obs,                //number of observations
          m_model_dof,          //degrees of freedom of model
          m_resid_dof,          //degrees of freedom of residuals
          m_kconstant,          //number of constants
          m_rank;               //rank of design matrix
   double m_aic,                //Akiake information criteria
          m_bic,                //Bayesian information criteria
          m_scale,              //scale of model
          m_llf,                //loglikelihood of model
          m_sse,                //sum of squared errors
          m_rsqe,               //r-squared of model
          m_centeredtss,        //centered sum of squares
          m_uncenteredtss;      //uncentered sum of squares
   uint              m_error;              //error flag
   // private methods
   ulong             countconstants(void);
   void              scale(void);
   void              sse(void);
   void              rsqe(void);
   void              centeredtss(void);
   void              uncenteredtss(void);
   void              aic(void);
   void              bic(void);
   void              bse(void);
   void              llf(void);
   void              tvalues(void);
   void              covariance_matrix(void);


public:
   //constructor
                     OLS(void);
   //destructor
                    ~OLS(void);
   //public methods
   bool              Fit(vector &y_vars,matrix &x_vars);
   double            Predict(vector &inputs);
   double            Predict(double _input);
   //get properties of OLS model
   ulong             ModelDOF(void) { if(m_error) return 0; else return m_model_dof;}
   ulong             ResidDOF(void) { if(m_error) return 0; else return m_resid_dof;}
   double            Scale(void)  { if(m_error) return EMPTY_VALUE; else return m_scale;    }
   double            Aic(void)    { if(m_error) return EMPTY_VALUE; else return m_aic;      }
   double            Bic(void)    { if(m_error) return EMPTY_VALUE; else return m_bic;    }
   double            Sse(void)    { if(m_error) return EMPTY_VALUE; else return m_sse;    }
   double            Rsqe(void)   { if(m_error) return EMPTY_VALUE; else return m_rsqe;   }
   double            C_tss(void)  { if(m_error) return EMPTY_VALUE; else return m_centeredtss;}
   double            Loglikelihood(void) { if(m_error) return EMPTY_VALUE; return m_llf; }
   vector            Tvalues(void) { if(m_error) return m_m_error.Col(0); return m_tvalues; }
   vector            Residuals(void) { if(m_error) return m_m_error.Col(0); return m_resid; }
   vector            ModelParameters(void) { if(m_error) return m_m_error.Col(0); return m_params; }
   vector            Bse(void) { if(m_error) return m_m_error.Col(0);  return m_bse; }
   matrix            CovarianceMatrix(void) { if(m_error) return m_m_error; return m_cov_params; }
  };

OLS.mqh contains the definition of the OLS class, representing an ordinary least squares regression model. The class has several public methods. The first of which is "Fit()", the first method that users should call after creating an instance of this class. It requires as input a vector and a matrix. The vector "y_vars" should be filled with the dependent values and "x_vars" is the design matrix ."Fit()" will return true on successful execution at which point any other public method can be called. All these methods return a specific property of a computed model. These properties are summarized in the table below.

Return data type	Value returned on error	Method	Description
ulong	0	ModelDOF()	the degress of freedom for a model
ulong	0	ResidDOF()	the degrees of freedom for a model's residuals
double	EMPTY_VALUE	Scale()	this is the variance of the error term, indicating the variability in the dependent variable not explained by the independent variables
double	EMPTY_VALUE	Aic()	Akaike's information criteria
double	EMPTY_VALUE	Bic()	Bayesian's information criteria
double	EMPTY_VALUE	Sse()	the sum of squared errors of the model
double	EMPTY_VALUE	Rsqe()	this is the R-squared metric of the model, ie the coefficient of determination
double	EMPTY_VALUE	C_tss()	this is the total sum of squared errors centred about the mean
double	EMPTY_VALUE	Loglikelihood()	The likelihood function for the OLS model
vector	vector of empty values	Tvalues()	provides the t-statistic for a each parameter estimate of a model
vector	vector of empty values	Residuals()	the residuals of the model, ie the difference between the predicted and actual values
vector	vector of empty values	Bse()	the standard errors of the parameter estimates
matrix	matrix of empty values	CovarianceMatrix()	matrix displaying the variances of variables and the covariances between the variables

 "Predict()" has two overloads that differ by their input data types. Which are either a vector or a scalar value of type double. Both return a single predition given new independent variable(s).

The next part of our implementation moves to the ADF.mqh file. This file will contain a collection of function definitions relating to the ADF test. One of these functions will be "adfuller()". We include OLS.mqh for the OLS class, Math.mqh from the standard library and also specialfunctions.mqh of the Alglib library.

//+------------------------------------------------------------------+
//|                                                          ADF.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\specialfunctions.mqh>
#include<OLS.mqh>

The next part of our implementation moves to the ADF.mqh file. This file will contain a collection of function definitions as well as that of the CAdf class. We include OLS.mqh for the OLS class, Math.mqh from the standard library and also specialfunctions.mqh of the Alglib library. ADF.mqh begins with the definition of some enumerations. ENUM_INFO_CRIT represents the options available when it comes to determining the optimal regression model for a particular series. It defines the metrics used to select the right model. ENUM_TRIM, ENUM_ORIGINAL, ENUM_HAS_CONST and ENUM_TREND are used in the construction of a design matrix. 

//+------------------------------------------------------------------+
//| Information criterion                                            |
//+------------------------------------------------------------------+
enum ENUM_INFO_CRIT
  {
   INFO_NONE=0,
   INFO_AIC,
   INFO_BIC
  };
//+------------------------------------------------------------------+
//| Options for  trimming invalid observations                       |
//+------------------------------------------------------------------+
enum ENUM_TRIM
  {
   TRIM_NONE=0,
   TRIM_FORWARD,
   TRIM_BACKWARD,
   TRIM_BOTH
  };
//+------------------------------------------------------------------+
//| options for how to handle original data set                      |
//+------------------------------------------------------------------+

enum ENUM_ORIGINAL
  {
   ORIGINAL_EX=0,
   ORIGINAL_IN,
   ORIGINAL_SEP
  };
//+------------------------------------------------------------------+
//| Constant and trend used in regression model                      |
//+------------------------------------------------------------------+

enum ENUM_TREND
  {
   TREND_NONE=0,
   TREND_CONST_ONLY,
   TREND_LINEAR_ONLY,
   TREND_LINEAR_CONST,
   TREND_QUAD_LINEAR_CONST
  };
//+------------------------------------------------------------------+
//| Options for how to handle existing constants                     |
//+------------------------------------------------------------------+

enum ENUM_HAS_CONST
  {
   HAS_CONST_RAISE=0,
   HAS_CONST_SKIP,
   HAS_CONST_ADD
  };

The "Adfuller()" method of CAdf returns a boolean value that signifies successfull execution of the test, NOT THE STATIONARITY OF A SERIES. If false is returned then an error must have occurred. Any errors will be accompanied by verbose messages output to the terminal's journal. It takes as input an array of a series to be analyzed.  Other arguments to the function are optional. In most cases users will not have to concern themselves with these parameters. Calling the function with the aforementioned parameters should suffice.

//+---------------------------------------------------------------------+
//|Class CAdf                                                           |
//|   encapsulates the the Augmented Dickey Fuller Test for Stationarity|
//+---------------------------------------------------------------------+

class CAdf
{
 private:
  double m_adf_stat,  //adf statistic
         m_bestic,    //optimal bic or aic
         m_pvalue;    //p-value
  ulong  m_usedlag;   //lag used for optimal reg model
  vector m_critvals;  //estimated critical values
  OLS    *m_ols;      //internal ordinary least squares reg model
   // private methods
 bool   gridsearch(vector &LHS, matrix &RHS, ulong f_lag, ulong l_lag,ENUM_INFO_CRIT crit, double &b_ic, ulong &best_lag);
 bool   lagmat(matrix &in,matrix &out[],ulong mlag,ENUM_TRIM trim=TRIM_BOTH,ENUM_ORIGINAL original=ORIGINAL_IN);
 bool   prepare_lhs_rhs(vector &lhs, matrix &rhs, double &in[], double &in_diff[],ulong lag);
 
 
 public:
  CAdf(void);
  ~CAdf(void);
  
 bool Adfuller(double &array[],ulong max_lag = 0,ENUM_TREND trend = TREND_CONST_ONLY, ENUM_INFO_CRIT autolag=INFO_AIC);
 vector CriticalValues(void) {  return m_critvals; }
 double AdfStatistic(void)   {  return m_adf_stat; }
 double Pvalue(void)         {  return m_pvalue;   }
};

"max_lag" defines the maximum number of lags of the regression model. "trend" is an enumeration that allows specification of the trend and constant configuration of the regression model."autolag" determines what metric is used to select the optimal model that best describes the input series. Within "Adfuller()", the function parameters are checked first before being used to construct the dependent and independent variables of a regression model.

Several variations of this initial design matrix are sampled in order to determine which one best fits the input series. The criteria used to come up with the best model is dependent on the value of the "autolag" parameter. The search is done by the "gridsearch()" function.

Once the best model is found, the lag property of this model, refering to the number of columns included from the initial design matrix, is used to define the optimal model. Whose parameters will be used to estimate the stationarity of the series. The first t-statistic of the optimal OLS model defines the ADF statistic of the ADF test. The p-value is computed by the "mackinnop()" function. Calling CAdf's "Pvalue()" method returns the corresponding p-value.

//+----------------------------------------------------------------------+
//| calculates MacKinnon's approximate p-value for a given test statistic|
//+----------------------------------------------------------------------+
double mackinnonp(double teststat, ENUM_TREND trend = TREND_CONST_ONLY,ulong nseries = 1, uint lags =0)
  {
   vector small_scaling =  {1, 1, 1e-2};
   vector large_scaling =  {1, 1e-1, 1e-1, 1e-2};

   double tau_star_nc []= {-1.04, -1.53, -2.68, -3.09, -3.07, -3.77};
   double tau_min_nc []= {-19.04, -19.62, -21.21, -23.25, -21.63, -25.74};
   double tau_max_nc []= {double("inf"), 1.51, 0.86, 0.88, 1.05, 1.24};
   double tau_star_c []= {-1.61, -2.62, -3.13, -3.47, -3.78, -3.93};
   double tau_min_c []= {-18.83, -18.86, -23.48, -28.07, -25.96, -23.27};
   double tau_max_c []= {2.74, 0.92, 0.55, 0.61, 0.79, 1};
   double tau_star_ct []= {-2.89, -3.19, -3.50, -3.65, -3.80, -4.36};
   double tau_min_ct []= {-16.18, -21.15, -25.37, -26.63, -26.53, -26.18};
   double tau_max_ct []= {0.7, 0.63, 0.71, 0.93, 1.19, 1.42};
   double tau_star_ctt []= {-3.21, -3.51, -3.81, -3.83, -4.12, -4.63};
   double tau_min_ctt []= {-17.17, -21.1, -24.33, -24.03, -24.33, -28.22};
   double tau_max_ctt []= {0.54, 0.79, 1.08, 1.43, 3.49, 1.92};

   double tau_nc_smallp [][3]=
     {
        {0.6344, 1.2378, 3.2496},
        {1.9129, 1.3857, 3.5322},
        {2.7648, 1.4502, 3.4186},
        {3.4336, 1.4835, 3.19},
        {4.0999, 1.5533, 3.59},
        {4.5388, 1.5344, 2.9807}
     };

   double tau_c_smallp [][3]=
     {
        {2.1659, 1.4412, 3.8269},
        {2.92, 1.5012, 3.9796},
        {3.4699, 1.4856, 3.164},
        {3.9673, 1.4777, 2.6315},
        {4.5509, 1.5338, 2.9545},
        {5.1399, 1.6036, 3.4445}
     };

   double tau_ct_smallp [][3]=
     {
        {3.2512, 1.6047, 4.9588},
        {3.6646, 1.5419, 3.6448},
        {4.0983, 1.5173, 2.9898},
        {4.5844, 1.5338, 2.8796},
        {5.0722, 1.5634, 2.9472},
        {5.53, 1.5914, 3.0392}
     };

   double tau_ctt_smallp [][3]=
     {
        {4.0003, 1.658, 4.8288},
        {4.3534, 1.6016, 3.7947},
        {4.7343, 1.5768, 3.2396},
        {5.214, 1.6077, 3.3449},
        {5.6481, 1.6274, 3.3455},
        {5.9296, 1.5929, 2.8223}
     };



   double tau_nc_largep [][4]=
     {
        {0.4797, 9.3557, -0.6999, 3.3066},
        {1.5578, 8.558, -2.083, -3.3549},
        {2.2268, 6.8093, -3.2362, -5.4448},
        {2.7654, 6.4502, -3.0811, -4.4946},
        {3.2684, 6.8051, -2.6778, -3.4972},
        {3.7268, 7.167, -2.3648, -2.8288}
     };

   double tau_c_largep [][4]=
     {
        {1.7339, 9.3202, -1.2745, -1.0368},
        {2.1945, 6.4695, -2.9198, -4.2377},
        {2.5893, 4.5168, -3.6529, -5.0074},
        {3.0387, 4.5452, -3.3666, -4.1921},
        {3.5049, 5.2098, -2.9158, -3.3468},
        {3.9489, 5.8933, -2.5359, -2.721}
     };

   double tau_ct_largep [][4]=
     {
        {2.5261, 6.1654, -3.7956, -6.0285},
        {2.85, 5.272, -3.6622, -5.1695},
        {3.221, 5.255, -3.2685, -4.1501},
        {3.652, 5.9758, -2.7483, -3.2081},
        {4.0712, 6.6428, -2.3464, -2.546},
        {4.4735, 7.1757, -2.0681, -2.1196}
     };

   double tau_ctt_largep [][4]=
     {
        {3.0778, 4.9529, -4.1477, -5.9359},
        {3.4713, 5.967, -3.2507, -4.2286},
        {3.8637, 6.7852, -2.6286, -3.1381},
        {4.2736, 7.6199, -2.1534, -2.4026},
        {4.6679, 8.2618, -1.822, -1.9147},
        {5.0009, 8.3735, -1.6994, -1.6928}
     };


   vector maxstat,minstat,starstat;
   matrix tau_smallps, tau_largeps;

   switch(trend)
     {
      case TREND_NONE:
         if(!maxstat.Assign(tau_max_nc) ||
            !minstat.Assign(tau_min_nc) ||
            !starstat.Assign(tau_star_nc)||
            !tau_smallps.Assign(tau_nc_smallp)||
            !tau_largeps.Assign(tau_nc_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_CONST_ONLY:
         if(!maxstat.Assign(tau_max_c) ||
            !minstat.Assign(tau_min_c) ||
            !starstat.Assign(tau_star_c)||
            !tau_smallps.Assign(tau_c_smallp)||
            !tau_largeps.Assign(tau_c_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ct) ||
            !minstat.Assign(tau_min_ct) ||
            !starstat.Assign(tau_star_ct)||
            !tau_smallps.Assign(tau_ct_smallp)||
            !tau_largeps.Assign(tau_ct_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_QUAD_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ctt) ||
            !minstat.Assign(tau_min_ctt) ||
            !starstat.Assign(tau_star_ctt)||
            !tau_smallps.Assign(tau_ctt_smallp)||
            !tau_largeps.Assign(tau_ctt_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      default:
         Print(__FUNCTION__," Error invalid input for trend argument");
         return double("nan");
     }

   if(teststat>maxstat[nseries-1])
      return 1.0;
   else
      if(teststat<minstat[nseries-1])
         return 0.0;


   vector tau_coef;

   if(teststat<=starstat[nseries-1])
      tau_coef = small_scaling*(tau_smallps.Row(nseries-1));
   else
      tau_coef = large_scaling*(tau_largeps.Row(nseries-1));


   double rv,tau[];

   ArrayResize(tau,int(tau_coef.Size()));

   for(ulong i=0; i<tau_coef.Size(); i++)
      tau[i]=tau_coef[tau_coef.Size()-1-i];

   rv=polyval(tau,teststat);

   return CNormalDistr::NormalCDF(rv);
  }

Whilst the critical values are calculated by "mackinnoncrit()". Whose results can be accessed through the CAdf method "CriticalValues()".

//+------------------------------------------------------------------+
//|Computes critical values                                          |
//+------------------------------------------------------------------+
vector mackinnoncrit(ulong nseries = 1,ENUM_TREND trend = TREND_CONST_ONLY, ulong num_obs=ULONG_MAX)
  {
   matrix tau_nc_2010 [] = {{
           {-2.56574, -2.2358, -3.627, 0},  // N [] = 1
           {-1.94100, -0.2686, -3.365, 31.223},
           {-1.61682, 0.2656, -2.714, 25.364}
        }
     };

   matrix tau_c_2010 [] =
     {
        {  {-3.43035, -6.5393, -16.786, -79.433},  // N [] = 1, 1%
           {-2.86154, -2.8903, -4.234, -40.040},   // 5 %
           {-2.56677, -1.5384, -2.809, 0}
        },        // 10 %
        {  {-3.89644, -10.9519, -33.527, 0},       // N [] = 2
           {-3.33613, -6.1101, -6.823, 0},
           {-3.04445, -4.2412, -2.720, 0}
        },
        {  {-4.29374, -14.4354, -33.195, 47.433},  // N [] = 3
           {-3.74066, -8.5632, -10.852, 27.982},
           {-3.45218, -6.2143, -3.718, 0}
        },
        {  {-4.64332, -18.1031, -37.972, 0},       // N [] = 4
           {-4.09600, -11.2349, -11.175, 0},
           {-3.81020, -8.3931, -4.137, 0}
        },
        {  {-4.95756, -21.8883, -45.142, 0},       // N [] = 5
           {-4.41519, -14.0405, -12.575, 0},
           {-4.13157, -10.7417, -3.784, 0}
        },
        {  {-5.24568, -25.6688, -57.737, 88.639},  // N [] = 6
           {-4.70693, -16.9178, -17.492, 60.007},
           {-4.42501, -13.1875, -5.104, 27.877}
        },
        {  {-5.51233, -29.5760, -69.398, 164.295},  // N [] = 7
           {-4.97684, -19.9021, -22.045, 110.761},
           {-4.69648, -15.7315, -5.104, 27.877}
        },
        {  {-5.76202, -33.5258, -82.189, 256.289},  // N [] = 8
           {-5.22924, -23.0023, -24.646, 144.479},
           {-4.95007, -18.3959, -7.344, 94.872}
        },
        {  {-5.99742, -37.6572, -87.365, 248.316},  // N [] = 9
           {-5.46697, -26.2057, -26.627, 176.382},
           {-5.18897, -21.1377, -9.484, 172.704}
        },
        {  {-6.22103, -41.7154, -102.680, 389.33},  // N [] = 10
           {-5.69244, -29.4521, -30.994, 251.016},
           {-5.41533, -24.0006, -7.514, 163.049}
        },
        {  {-6.43377, -46.0084, -106.809, 352.752},  // N [] = 11
           {-5.90714, -32.8336, -30.275, 249.994},
           {-5.63086, -26.9693, -4.083, 151.427}
        },
        {  {-6.63790, -50.2095, -124.156, 579.622},  // N [] = 12
           {-6.11279, -36.2681, -32.505, 314.802},
           {-5.83724, -29.9864, -2.686, 184.116}
        }
     };

   matrix tau_ct_2010 [] =
     {
        {  {-3.95877, -9.0531, -28.428, -134.155},   // N [] = 1
           {-3.41049, -4.3904, -9.036, -45.374},
           {-3.12705, -2.5856, -3.925, -22.380}
        },
        {  {-4.32762, -15.4387, -35.679, 0},         // N [] = 2
           {-3.78057, -9.5106, -12.074, 0},
           {-3.49631, -7.0815, -7.538, 21.892}
        },
        {  {-4.66305, -18.7688, -49.793, 104.244},   // N [] = 3
           {-4.11890, -11.8922, -19.031, 77.332},
           {-3.83511, -9.0723, -8.504, 35.403}
        },
        {  {-4.96940, -22.4694, -52.599, 51.314},    // N [] = 4
           {-4.42871, -14.5876, -18.228, 39.647},
           {-4.14633, -11.2500, -9.873, 54.109}
        },
        {  {-5.25276, -26.2183, -59.631, 50.646},    // N [] = 5
           {-4.71537, -17.3569, -22.660, 91.359},
           {-4.43422, -13.6078, -10.238, 76.781}
        },
        {  {-5.51727, -29.9760, -75.222, 202.253},   // N [] = 6
           {-4.98228, -20.3050, -25.224, 132.03},
           {-4.70233, -16.1253, -9.836, 94.272}
        },
        {  {-5.76537, -33.9165, -84.312, 245.394},   // N [] = 7
           {-5.23299, -23.3328, -28.955, 182.342},
           {-4.95405, -18.7352, -10.168, 120.575}
        },
        {  {-6.00003, -37.8892, -96.428, 335.92},    // N [] = 8
           {-5.46971, -26.4771, -31.034, 220.165},
           {-5.19183, -21.4328, -10.726, 157.955}
        },
        {  {-6.22288, -41.9496, -109.881, 466.068},  // N [] = 9
           {-5.69447, -29.7152, -33.784, 273.002},
           {-5.41738, -24.2882, -8.584, 169.891}
        },
        {  {-6.43551, -46.1151, -120.814, 566.823},  // N [] = 10
           {-5.90887, -33.0251, -37.208, 346.189},
           {-5.63255, -27.2042, -6.792, 177.666}
        },
        {  {-6.63894, -50.4287, -128.997, 642.781},  // N [] = 11
           {-6.11404, -36.4610, -36.246, 348.554},
           {-5.83850, -30.1995, -5.163, 210.338}
        },
        {  {-6.83488, -54.7119, -139.800, 736.376},  // N [] = 12
           {-6.31127, -39.9676, -37.021, 406.051},
           {-6.03650, -33.2381, -6.606, 317.776}
        }
     };

   matrix tau_ctt_2010 [] =
     {
        {  {-4.37113, -11.5882, -35.819, -334.047},  // N [] = 1
           {-3.83239, -5.9057, -12.490, -118.284},
           {-3.55326, -3.6596, -5.293, -63.559}
        },
        {  {-4.69276, -20.2284, -64.919, 88.884},    // N [] =2
           {-4.15387, -13.3114, -28.402, 72.741},
           {-3.87346, -10.4637, -17.408, 66.313}
        },
        {  {-4.99071, -23.5873, -76.924, 184.782},   // N [] = 3
           {-4.45311, -15.7732, -32.316, 122.705},
           {-4.17280, -12.4909, -17.912, 83.285}
        },
        {  {-5.26780, -27.2836, -78.971, 137.871},   // N [] = 4
           {-4.73244, -18.4833, -31.875, 111.817},
           {-4.45268, -14.7199, -17.969, 101.92}
        },
        {  {-5.52826, -30.9051, -92.490, 248.096},   // N [] = 5
           {-4.99491, -21.2360, -37.685, 194.208},
           {-4.71587, -17.0820, -18.631, 136.672}
        },
        {  {-5.77379, -34.7010, -105.937, 393.991},  // N [] = 6
           {-5.24217, -24.2177, -39.153, 232.528},
           {-4.96397, -19.6064, -18.858, 174.919}
        },
        {  {-6.00609, -38.7383, -108.605, 365.208},  // N [] = 7
           {-5.47664, -27.3005, -39.498, 246.918},
           {-5.19921, -22.2617, -17.910, 208.494}
        },
        {  {-6.22758, -42.7154, -119.622, 421.395},  // N [] = 8
           {-5.69983, -30.4365, -44.300, 345.48},
           {-5.42320, -24.9686, -19.688, 274.462}
        },
        {  {-6.43933, -46.7581, -136.691, 651.38},   // N [] = 9
           {-5.91298, -33.7584, -42.686, 346.629},
           {-5.63704, -27.8965, -13.880, 236.975}
        },
        {  {-6.64235, -50.9783, -145.462, 752.228},  // N [] = 10
           {-6.11753, -37.056, -48.719, 473.905},
           {-5.84215, -30.8119, -14.938, 316.006}
        },
        {  {-6.83743, -55.2861, -152.651, 792.577},  // N [] = 11
           {-6.31396, -40.5507, -46.771, 487.185},
           {-6.03921, -33.8950, -9.122, 285.164}
        },
        {  {-7.02582, -59.6037, -166.368, 989.879},  // N [] = 12
           {-6.50353, -44.0797, -47.242, 543.889},
           {-6.22941, -36.9673, -10.868, 418.414}
        }
     };

   vector ret_vector = {0,0,0};

   switch(trend)
     {
      case TREND_CONST_ONLY:
         process(tau_c_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_NONE:
         process(tau_nc_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_LINEAR_CONST:
         process(tau_ct_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_QUAD_LINEAR_CONST:
         process(tau_ctt_2010,ret_vector,num_obs,nseries);
         break;
      default:
         Print("Invalid input for trend argument");
         return ret_vector;
     }

   return ret_vector;
  }

Testing and validation

To validate that our implementation is running correctly we will first conduct an ADF test in Python, on a random series. Then we will run the ADF test on the same series in Metatrader 5 and compare the output.

The code for the ADF test in Python is listed below.

import numpy as np
from statsmodels.tsa.stattools import adfuller

#initialize array with 100 elements
x = np.array([0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
              0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
              0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
              0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
              0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
              0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
              0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
              0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
              0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
              0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
              0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
              0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
              0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
              0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
              0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
              0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
              0.20684364,0.29630613,0.65178447,0.86559185])
   
#perform ADF test on array 
result = adfuller(x)

#print ADF statistic and p-value
print(f"ADF statistic: {result[0]}, p-value:{result[1]}")

#print critical values
print(f"Critical values:{result[4]}")
   

Next, we run the MQL5 version of ADF test on the same array, the script program code is shown below.

//+------------------------------------------------------------------+
//|                                                     ADF_test.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<ADF.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---series
   double rand_array[] =
     {
      0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
      0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
      0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
      0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
      0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
      0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
      0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
      0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
      0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
      0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
      0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
      0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
      0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
      0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
      0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
      0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
      0.20684364,0.29630613,0.65178447,0.86559185
     };

//---variables that will be used to store test results
   CAdf adf;
//--- Do ADF test
   if(adf.Adfuller(rand_array))
      Print("ADF test statistic: ", adf.AdfStatistic(), " P-value:", adf.Pvalue(),"\nCritical values \n",adf.CriticalValues());
   else
      Print("ADF test failed");
  }
//+------------------------------------------------------------------+

Running the python script first:

LD      0       18:30:22.912    Test_adfuller (NFLX_us,Daily)   ADF statistic: -8.495443215534635, p-value:1.2796318143567197e-13
GJ      0       18:30:22.913    Test_adfuller (NFLX_us,Daily)   Critical values:{'1%': -3.4989097606014496, '5%': -2.891516256916761, '10%': -2.5827604414827157}

And then the MetaTrader 5 script next , we can see the results are the same.

DO      0       18:30:48.460    ADF_test (NFLX_us,D1)   ADF test statistic: -8.495443215534634 P-value:1.2796318143567197e-13
ND      0       18:30:48.460    ADF_test (NFLX_us,D1)   Critical values 
OL      0       18:30:48.460    ADF_test (NFLX_us,D1)   [-3.49890976060145,-2.891516256916761,-2.582760441482716]

Cointegration

Correlation and cointegration are statistical concepts used to measure relationships between variables, especially in the context of time series data. While both measure relationships, they serve different purposes and are applied in distinct scenarios. Correlation refers to the statistical measure of the strength and direction of the linear relationship between two variables.

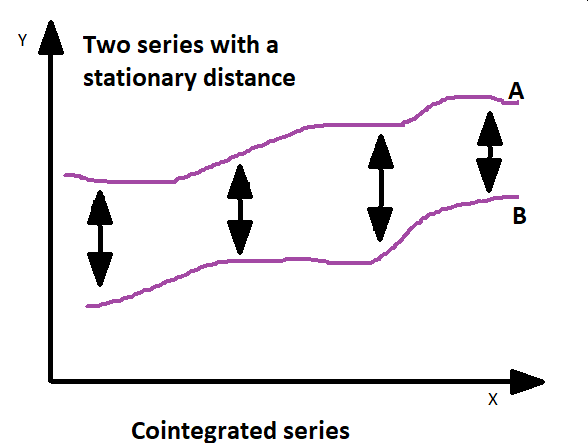
Cointegration, on the other hand, deals with the relationship between non-stationary time series variables that possess a long-term equilibrium or steady relationship. In simpler terms, it identifies whether there exists a combination of two or more non-stationary variables that have a stable, long-run relationship when considered together. Cointegration is useful in identifying pairs of variables that move together over time, despite short-term fluctuations. It implies that the variables are linked in the long run, making it possible to exploit this relationship for trading strategies or modeling.

Cointegration is typically assessed using statistical tests like the Engle-Granger test or Johansen test. These tests check if a linear combination of non-stationary variables creates a stationary series, indicating a long-term relationship. The Engle-Granger test is a two-step procedure to test for cointegration between two variables in a time series setting. It involves estimating a regression model and then conducting tests on the residuals to determine whether cointegration exists. If the residuals of the regression model are found to be stationary, it suggests cointegration between the two variables. In this case, it indicates that despite the variables not being individually stationary, a linear combination of them is stationary.

The Engle-Granger test is limited in that it cannot handle multiple sequences simultaneously. This limitation is adressed by the Johansen test. Which is essentially an extension of the Engle-Granger approach to test for cointegration among multiple series in a vector autoregressive model. We will not be looking at the Johansen test in this article, we limit ourselves to dealing with only two series at a time.

CointegrationTest.mqh contains the function CCoint class. It implements the augmented Engle-Granger test with the help of the CAdf class. The test is conducted by calling CCoint's "Aeg()" method. Two input arrays containing series to be tested are required. The optional input parameters "trend", "max_lag", and "autolag", are similar to the parameters of the "Adfuller()" method in CAdf. Again for most tests the default values should be sufficient. As it will be demonstrated in the next section.  The results of the cointegration test are obtained by calling three methods of CCoint. The first "CointStatistic", returns the ADF statistic from the internal ADF test. "CriticalValues()" returns a vector of the critical values of the test. The p-value can be obtained by calling "Pvalue()".

//+------------------------------------------------------------------+
//|                                            CointegrationTest.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<ADF.mqh>

//+------------------------------------------------------------------+
//|Class CCoint                                                      |
//|    implements cointegration test of two series                   |
//+------------------------------------------------------------------+
class CCoint
{
 private:
  double m_coint_stat;       //ADF test statistic
  double m_coint_pvalue;     //cointegration p-value
  vector m_coint_critvalues; //Cointegration critical values
  CAdf   *m_adf;             //CAdf object pointer
 public:
  CCoint(void);
  ~CCoint(void);
  
  bool Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC);
  
  double CointStatistic(void){ return m_coint_stat; }
  double Pvalue(void)        { return m_coint_pvalue;}
  vector CriticalValues(void){ return m_coint_critvalues;}
};
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CCoint::CCoint(void)
{
 m_adf = new CAdf();
 
 m_coint_critvalues = vector::Zeros(3);
 
 m_coint_stat=m_coint_pvalue=EMPTY_VALUE;
}
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CCoint::~CCoint(void)
{
 if(CheckPointer(m_adf)==POINTER_DYNAMIC)
     delete m_adf;
}
//+------------------------------------------------------------------+
//| Test for cointegration                                           |
//+------------------------------------------------------------------+
bool CCoint::Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC)
  {
//---  
   if(CheckPointer(m_adf)==POINTER_INVALID)
    {
     Print("Critical Internal error: Invalid CAdf pointer");
     return false;
    }
//---    
   if(in_one.Size()<1 || in_two.Size()<1 || in_one.Size()!=in_two.Size())
     {
      Print(__FUNCTION__," Invalid input for one or both arrays");
      return false;
     }

   vector y1,temp;
   matrix y2;

   if(!y1.Assign(in_one) || !temp.Assign(in_two) || !y2.Resize(temp.Size(),1) || !y2.Col(temp,0))
     {
      Print(__FUNCTION__," Assignment error: ", GetLastError());
      return false;
     }


   ulong obs,kvars=1;
   obs = y2.Rows();
   kvars++;
   matrix xx;

   if(trend==TREND_NONE)
     {
      if(!xx.Copy(y2))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }
     }
   else
    if(!addtrend(y2,xx,trend,false))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }

   OLS ols;

   if(!ols.Fit(y1,xx))
      return false;

   if(ols.Rsqe()< 1 - 100*SQRTEPS)
     {
      double resid[];

      vector resd = ols.Residuals();

      ArrayResize(resid,int(resd.Size()));

      for(uint i = 0; i<resid.Size(); i++)
         resid[i]=resd[i];

      if(!m_adf.Adfuller(resid,max_lag,TREND_NONE,autolag))
         return false;

      m_coint_stat = m_adf.AdfStatistic();
     }
   else
     {
      Print("They are (almost) perfectly collinear.\nCointegration test is not reliable in this case");
      m_coint_stat=double("nan");
     }

   if(trend==TREND_NONE)
      m_coint_critvalues.Fill(double("nan"));
   else
      m_coint_critvalues = mackinnoncrit(kvars,trend,obs-1);

   m_coint_pvalue = mackinnonp(m_coint_stat,trend,kvars);

   return true;
  }    

Testing symbols for cointegration

For the final demonstration we will create a MQL5 script that uses  CCoint to test a list of symbols for cointegration. Users input a list of symbols, delimited by commas. Set the start date and history length of the close prices to be studied. "ConfidenceLevel" enables users to select the desired level of significance. This determines the critical value that will be compared to the ADF statistic for the final result.

//+------------------------------------------------------------------+
//|                                    SymbolCointegrationTester.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <CointegrationTest.mqh>
//+------------------------------------------------------------------+
//| enumeration maps to confidence levels of 99%,95%, and 90%        |
//+------------------------------------------------------------------+
enum ENUM_CONFIDENCE_LEVEL
  {
   CONF_99=0,//99%
   CONF_95,//95%
   CONF_90 //90%
  };
//--- input parameters
input string   Symbols = "FB_us,GOOG_us,MSFT_us,NFLX_us,NVDA_us,AAPL_us,TSLA_us";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2022.01.01 00:00:01';
input int Size = 250;//History length
input ENUM_CONFIDENCE_LEVEL ConfidenceLevel=CONF_90;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(Size<100)
     {
      Print("Invalid input for Size");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;

//---in case there are less than two symbols specified
   if(num_symbols<2)
     {
      Print("Invalid input. Please list at least two symbols");
      return;
     }
//---output matrix of indices
   matrix sym_combos;
//---fill sym_combos with index values of symbols array
   PairedCombinations(symbols,sym_combos,num_symbols);
//---price arrays for pair of symbols
   double symA_prices [], symB_prices[];
//---output vectors holding results of cointegration test
   vector stats, critvals;
//---symbol pairs and result output
   string symA,symB,result;
//---CCoint object
   CCoint coint;
//---loop through all paired combinations from list
   for(ulong i=0; i<sym_combos.Rows(); i++)
     {
      //--- get symbol pair for current combination
      symA = symbols[int(sym_combos[i][0])];
      symB = symbols[int(sym_combos[i][1])];
      //--- get prices for the pair of symbols
      if(CopyClose(symA,TimeFrame,StartDate,Size,symA_prices)<Size||
         CopyClose(symB,TimeFrame,StartDate,Size,symB_prices)<Size)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //--- test the pair for cointegreation
      if(!coint.Aeg(symA_prices,symB_prices))
        {
         Print("Cointegration test failed ", ::GetLastError());
         return;
        }
      //---
      vector critvals = coint.CriticalValues();
      //--- prepare results output for a test
      if(coint.CointStatistic()<critvals[ConfidenceLevel])
         result="likely cointegrated.";
      else
         result="likely not cointegrated.";
      //--- output the result from cointegration test
      Print(symA," and ",symB, " are ", result);
     }
  }
//+------------------------------------------------------------------+
//| Combinations: generates paired combinations                      |
//+------------------------------------------------------------------+
bool PairedCombinations(string &in[], matrix &out,int count = 0)
  {
//---check input array
   if(in.Size()<1)
     {
      Print(__FUNCTION__," input array is empty");
      return false;
     }
//---set value for upto equal to the number of elements that should be
//---considered in the input array
   int upto = (count>1 && count<ArraySize(in))?count:ArraySize(in);
//--- calculate the number of rows equivalent to number of combinations
   ulong rows = ulong(MathFactorial(upto)/(MathFactorial(2)*MathFactorial(upto-2)));
//---resize output matrix accordingly
   out.Resize(rows,2);
//---fill output matrix with indexes of input array
   for(uint i=0,z=0; i<in.Size(); i++)
     {
      for(uint k = i+1; k<in.Size(); k++,z++)
        {
         out[z][0]=i;
         out[z][1]=k;
        }
     }
//---return
   return true;
  }
//+------------------------------------------------------------------+

In our example we will test the symbols Google,Facebook,Microsoft,NetFlix,Nvidia,Apple and Tesla. The results from running script are shown below.

HN      0       18:37:31.239    SymbolCointegrationTester (NFLX_us,D1)  FB_us and GOOG_us are likely not cointegrated.
PQ      0       18:37:31.280    SymbolCointegrationTester (NFLX_us,D1)  FB_us and MSFT_us are likely not cointegrated.
IE      0       18:37:31.322    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NFLX_us are likely not cointegrated.
MG      0       18:37:31.365    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NVDA_us are likely not cointegrated.
PH      0       18:37:31.411    SymbolCointegrationTester (NFLX_us,D1)  FB_us and AAPL_us are likely not cointegrated.
NL      0       18:37:31.453    SymbolCointegrationTester (NFLX_us,D1)  FB_us and TSLA_us are likely not cointegrated.
EO      0       18:37:31.496    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and MSFT_us are likely not cointegrated.
ES      0       18:37:31.540    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NFLX_us are likely not cointegrated.
FE      0       18:37:31.582    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NVDA_us are likely not cointegrated.
CF      0       18:37:31.623    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and AAPL_us are likely not cointegrated.
EJ      0       18:37:31.665    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and TSLA_us are likely not cointegrated.
HM      0       18:37:31.705    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NFLX_us are likely not cointegrated.
RN      0       18:37:31.744    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NVDA_us are likely not cointegrated.
LP      0       18:37:31.785    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and AAPL_us are likely not cointegrated.
OD      0       18:37:31.825    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and TSLA_us are likely not cointegrated.
IG      0       18:37:31.866    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and NVDA_us are likely not cointegrated.
QI      0       18:37:31.906    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and AAPL_us are likely not cointegrated.
FP      0       18:37:31.946    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and TSLA_us are likely cointegrated.
EO      0       18:37:31.987    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and AAPL_us are likely not cointegrated.
RS      0       18:37:32.026    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and TSLA_us are likely not cointegrated.
DE      0       18:37:32.072    SymbolCointegrationTester (NFLX_us,D1)  AAPL_us and TSLA_us are likely not cointegrated.

They show that NetFlix and Tesla are likely cointegrated at a confidence level of 90%.

The code for conducting the same test in Python follows, along with the results.

"""
 Script demonstrates use of coint() from statsmodels
 to test symbols for cointegration
"""
# imports 
from statsmodels.tsa.stattools import coint
from itertools import combinations
from datetime import datetime
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import pytz

#initialize connection to mt5
if not mt5.initialize():
    print("initialize() failed ")
    mt5.shutdown()
 
#set up timezone infomation   
tz=pytz.timezone("Etc/UTC")

#use time zone to set correct date for history data extraction
startdate = datetime(2022,1,1,hour=0,minute=0,second=1,tzinfo=tz)

#list the symbols 
Symbols = ["FB_us","GOOG_us","MSFT_us","NFLX_us","NVDA_us","AAPL_us","TSLA_us"]

#set length of data history
num_bars = 250

#set up the shape of the data structure to store prices 
data = np.zeros((num_bars,len(Symbols)))
prices = pd.DataFrame(data,columns=Symbols)

#fill prices dataframe with close prices
for symbol in Symbols:
    prices[symbol]=[rate[4]  for rate in mt5.copy_rates_from(symbol,mt5.TIMEFRAME_D1,startdate,num_bars)]
    
#we donot need mt5 from here 
mt5.shutdown()

#generate pairs from Symbols list 
pairs = list(combinations(prices.columns,2))

#set our desired significance level, 0.01->99%, 0.05->95%, 0.1->90%
confidence_level = 0.1

#do the test for cointegration on each pair and print results
for pair in pairs:
    df=prices[list(pair)]
    adf_stat,pvalue,critvalues=coint(df.values[:,0],df.values[:,1])
    if pvalue < confidence_level:
        print(pair[0]," and ",pair[1], " are likely cointegrated")
    else:
        print(pair[0]," and ",pair[1], " are likely not cointegrated")   

Python results

MR      0       18:35:17.835    SymbolCointegration (NFLX_us,Daily)     FB_us  and  GOOG_us  are likely not cointegrated
GE      0       18:35:17.851    SymbolCointegration (NFLX_us,Daily)     FB_us  and  MSFT_us  are likely not cointegrated
DI      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NFLX_us  are likely not cointegrated
CJ      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NVDA_us  are likely not cointegrated
MO      0       18:35:17.882    SymbolCointegration (NFLX_us,Daily)     FB_us  and  AAPL_us  are likely not cointegrated
JQ      0       18:35:17.898    SymbolCointegration (NFLX_us,Daily)     FB_us  and  TSLA_us  are likely not cointegrated
CD      0       18:35:17.914    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  MSFT_us  are likely not cointegrated
MF      0       18:35:17.930    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NFLX_us  are likely not cointegrated
QK      0       18:35:17.946    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NVDA_us  are likely not cointegrated
HM      0       18:35:17.962    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  AAPL_us  are likely not cointegrated
OO      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  TSLA_us  are likely not cointegrated
MS      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NFLX_us  are likely not cointegrated
PD      0       18:35:17.994    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NVDA_us  are likely not cointegrated
MF      0       18:35:18.010    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  AAPL_us  are likely not cointegrated
RJ      0       18:35:18.042    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  TSLA_us  are likely not cointegrated
RM      0       18:35:18.058    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  NVDA_us  are likely not cointegrated
GP      0       18:35:18.074    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  AAPL_us  are likely not cointegrated
LN      0       18:35:18.089    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  TSLA_us  are likely cointegrated
EF      0       18:35:18.105    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  AAPL_us  are likely not cointegrated
QI      0       18:35:18.121    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  TSLA_us  are likely not cointegrated
OJ      0       18:35:18.137    SymbolCointegration (NFLX_us,Daily)     AAPL_us  and  TSLA_us  are likely not cointegrated

Conclusion

So far we have looked at the implementation of the Augmented Dickey-Fuller in MQL5 and used it to implement Engle-Granger's test for cointegration. The ADF test is an important tool for those interested in exploring pairs trading strategies or statistical arbitrage.  All the code described in the article is enclosed in the zip file. The table below lists all the contents of this file.

File	Description
Mql5\include\OLS.mqh	Contains the definition of the OLS class, which implements ordinary least squares regression
Mql5\include\ADF.mqh	Contains the definition of variousfunctions and the CAdf class implementing the ADF test
Mql5\include\CointegrationTest.mqh	Defines the CCoint class which implements a cointegration test using the Augmented Engle-Granger technique
Mql5\scripts\ADF_test.mq5	This is the MQL5 script used to test the MQL5 implementation of the ADF test
Mql5\scripts\SymbolCointegrationTester.mq5	script for testing symbols in MetaTrader 5 for cointegration
Mql5\scripts\Test_adfuller.py	Is a python script using the statsmodels implementation of the ADF test used to validate our MQL5 implementation
Mql5\scripts\SymbolCointegration.py	Python version of SymbolCointegrationTester