Implementierung des Augmented Dickey Fuller-Tests in MQL5

Einführung

Der Test Augmented Dickey-Fuller (ADF) ist ein gängiges Verfahren, um zu beurteilen, ob eine Zeitreihe stationär ist oder nicht.  Es ist jedoch bekannt, dass Finanzzeitreihen von Natur aus nicht stationär sind. Viele statistische Methoden, die von der Stationarität profitieren, erfordern in der Regel, dass nicht-stationäre Datensätze vor der Analyse auf irgendeine Weise transformiert werden. Der ADF-Test kann verwendet werden, um die Wirksamkeit dieser Umformungen bei der Herstellung von Stationarität zu bewerten. Alternativ werden bei der Bewertung der Kointegration von Reihen auch Stationaritätstests verwendet. Nützlich bei der Entwicklung von Handelsstrategien, die Diskrepanzen in der Preisbildung von verwandten Finanzinstrumenten ausnutzen. In diesem Artikel stellen wir die Implementierung des ADF-Tests in MQL5 vor und demonstrieren seine Anwendung, indem wir ihn zur Identifizierung kointegrierter Symbole in MetaTrader 5 verwenden.

Verstehen des ADF-Tests

Einfach ausgedrückt ist ein ADF-Test ein Hypothesentest, mit dem wir feststellen können, ob ein bestimmtes Merkmal der beobachteten Daten statistisch signifikant ist. In diesem Fall ist das zu ermittelnde Merkmal die Stationarität einer Reihe.  Eine statistische Hypothese ist eine Annahme über einen Datensatz, der durch eine Stichprobe repräsentiert wird. Wir können die wirkliche Wahrheit nur erfahren, wenn wir mit dem gesamten Datensatz arbeiten. Was in der Regel aus dem einen oder anderen Grund nicht möglich ist. Es wird also eine Stichprobe eines Datensatzes getestet, um eine Annahme für den gesamten Datensatz zu treffen. Es ist wichtig, sich daran zu erinnern, dass der Wahrheitsgehalt einer statistischen Hypothese bei der Arbeit mit Stichproben nie mit Gewissheit feststeht. Was wir erhalten, ist, ob eine Annahme wahrscheinlich wahr oder falsch ist.

Bei einem ADF-Test betrachten wir zwei Szenarien:

• Die Nullhypothese, dass eine „Einheitswurzel“ in der Zeitreihe vorhanden ist.

• Die Alternativhypothese, dass die Zeitreihe keine „Einheitswurzel“ aufweist.

In der Zeitreihenanalyse ist eine Einheitswurzel ein besonderes Merkmal eines sequenziellen Datensatzes. Stellen Sie sich vor, ein Mann geht mit seinem Hund eine Straße entlang. Der Mann wird wahrscheinlich in einer ziemlich geraden Linie auf sein Ziel zugehen. Dabei läuft der Hund oft weg, um an etwas zu schnüffeln oder ein Tier zu jagen, das seine Aufmerksamkeit erregt hat. Aber letztendlich wird er seinem Besitzer folgen. Wenn man den Weg des Hundes aufzeichnet, kann man eine Art von Schwingung beobachten. Der Hund entfernt sich, kehrt aber schließlich in die erwartete Richtung seines Herrchen zurück.

Ein beliebiger Punkt auf dem Weg des Hundes stellt den Wert einer Variablen zu einem bestimmten Zeitpunkt dar. Wenn wir diese Werte auswerten, ist es wahrscheinlich, dass sie in einem bestimmten Bereich um eine zentrale Tendenz herum liegen. Die statistischen Eigenschaften ändern sich im Laufe der Zeit nicht wesentlich. Eine solche Reihe wird keine Einheitswurzel haben. Stellen Sie sich nun vor, der Mann würde mit seinem untrainierten Hund auf der gleichen Straße spazieren gehen. Der Hund wird wahrscheinlich weglaufen und nicht mehr zu seinem Herrchen zurückkehren. Die Werte, die mit dem von diesem Hund eingeschlagenen Weg verbunden sind, werden auf unvorhersehbare Weise variieren. Eine solche Reihe wird eine Einheitswurzel haben.

Der Begriff der Einheitswurzel stammt aus der charakteristischen Gleichung eines stochastischen Prozesses. Ein stochastischer Prozess ist eine Folge von Variablen, die durch die Zeit indiziert sind und ein System beschreiben, das sich zufällig entwickelt. Die charakteristische Gleichung eines stochastischen Prozesses ist eine Gleichung, die die Eigenschaften des Systems erfasst. Die Einheitswurzel ist eine Lösung der charakteristischen Gleichung, die gleich 1 ist. Wenn ein Prozess eine Einheitswurzel hat, bedeutet dies, dass die Schocks oder zufälligen Effekte eine dauerhafte Wirkung auf den Prozess haben. Ein solches System wird durch Zufallseffekte und verzögerte Werte modelliert. Das bedeutet, dass es sich um eine autoregressive Entwicklung handelt.

Daher wird beim ADF-Test ein Regressionsmodell verwendet, um auf eine Einheitswurzel zu testen. Die gebräuchlichste Form des Modells ergibt sich aus der nachstehenden Gleichung.

Wobei:

• „Y“ Die erste Differenz der Zeitreihe
  

•  „a“ Ein konstanter Term

•  „b“ Der Koeffizient des verzögerten Niveaus der Zeitreihe
  

•  „x“ Der Koeffizient des Zeittrends (t)

•  „V“ Koeffizienten der verzögerten ersten Differenzen
  

•  „E“ Der Fehlerterm

Der Test konzentriert sich auf den Koeffizienten „b“. Wenn „b“ = 0 ist, liegt eine Einheitswurzel vor, wenn „b“ < 0 ist, ist die Zeitreihe stationär. Die ADF-Statistik wird auf der Grundlage des geschätzten Wertes von „b“ und dessen Standardfehler berechnet. Er wird mit kritischen Werten aus einer Dickey-Fuller-Verteilung verglichen. Wenn die ADF-Statistik bei einem bestimmten Signifikanzniveau negativer ist als der kritische Wert, wird die Nullhypothese einer Einheitswurzel verworfen. Das bedeutet, dass die Reihe stationär ist.

Umsetzung

Um sicherzustellen, dass unsere Implementierung genau ist, werden wir eine bestehende Implementierung des ADF-Tests in Python als Referenz verwenden. Im Python-Paket statsmodels wird die Funktion „adfuller“ zur Durchführung eines ADF-Tests verwendet.

adfuller(x, maxlag: 'int | None' = None, regression='c', autolag='AIC', store=False, regresults=False)

Die Funktion schätzt zunächst die Parameter eines autoregressiven Modells der Eingangsreihen mit Hilfe der gewöhnlichen kleinsten Quadrate. Auf der Grundlage der geschätzten Parameter wird eine Teststatistik berechnet. Dieser wird zur Berechnung eines p-Wertes verwendet. Aus einer Verteilungstabelle werden drei kritische Werte gezogen, die Konfidenzniveaus darstellen. Schließlich kann die Teststatistik mit jedem dieser Werte verglichen werden, um festzustellen, ob eine Reihe stationär ist oder nicht.

Ausgehend von diesem Überblick gibt es drei wichtige Komponenten, die wir umsetzen müssen. Das erste ist das gewöhnliche Regressionsmodell nach der Methode der kleinsten Quadrate. Wahrscheinlich die wichtigste Komponente, da sich Fehler in diesem Bereich auf andere Phasen des Tests auswirken. Dies wird verwendet, um das am besten geeignete autoregressive Modell für die zu analysierende Reihe zu bestimmen. Neben den Modellparametern müssen wir auch verschiedene Eigenschaften eines Modells berechnen, wie z. B. die Akaike-Informationskriterien und die Bayes'schen Informationskriterien.

Die zweite Komponente bezieht sich auf die Berechnung des p-Wertes. Der p-Wert wird durch eine Teststatistik bestimmt, die aus der t-Statistik des optimalen autoregressiven Modells abgeleitet wird. Eine t-Statistik ist ein Maß, mit dem festgestellt werden kann, ob ein signifikanter Unterschied zwischen den Mittelwerten zweier Gruppen besteht. Er wird berechnet, indem die Differenz zwischen den Stichprobenmittelwerten durch den Standardfehler der Differenz geteilt wird. In diesem Zusammenhang wird die t-Statistik berechnet, indem die Parameter des Modells durch den Standardfehler des Modells dividiert werden. Die zur Berechnung des p-Wertes verwendete Methode wurde von J.G. MacKinnon vorgeschlagen und wird daher als MacKinnon's approximative p-Wert-Methode bezeichnet. Sie liefert eine Annäherung an den p-Wert, der mit kritischen Werten aus statistischen Tests verbunden ist.

Die letzte Komponente, die zur Vervollständigung des ADF-Tests benötigt wird, ist die Berechnung der kritischen Werte. Diese Werte sind von Näherungswerten abgeleitet, die in einem von MacKinnon verfassten wissenschaftlichen Artikel angegeben sind.

//+------------------------------------------------------------------+
//| Ordinary least squares class                                     |
//+------------------------------------------------------------------+
class OLS
  {
private:
   matrix m_exog,               //design matrix
          m_pinv,               //pseudo-inverse of matrix
          m_cov_params,         //covariance of matrix
          m_m_error,            //error matrix
          m_norm_cov_params;    //normalized covariance matrix
   vector m_endog,              //dependent variables
          m_weights,            //weights
          m_singularvalues,     //singular values of solution
          m_params,             //coefficients of regression model(solution)
          m_tvalues,            //test statistics of model
          m_bse,                //standard errors of model
          m_resid;              //residuals of model
   ulong  m_obs,                //number of observations
          m_model_dof,          //degrees of freedom of model
          m_resid_dof,          //degrees of freedom of residuals
          m_kconstant,          //number of constants
          m_rank;               //rank of design matrix
   double m_aic,                //Akiake information criteria
          m_bic,                //Bayesian information criteria
          m_scale,              //scale of model
          m_llf,                //loglikelihood of model
          m_sse,                //sum of squared errors
          m_rsqe,               //r-squared of model
          m_centeredtss,        //centered sum of squares
          m_uncenteredtss;      //uncentered sum of squares
   uint              m_error;              //error flag
   // private methods
   ulong             countconstants(void);
   void              scale(void);
   void              sse(void);
   void              rsqe(void);
   void              centeredtss(void);
   void              uncenteredtss(void);
   void              aic(void);
   void              bic(void);
   void              bse(void);
   void              llf(void);
   void              tvalues(void);
   void              covariance_matrix(void);


public:
   //constructor
                     OLS(void);
   //destructor
                    ~OLS(void);
   //public methods
   bool              Fit(vector &y_vars,matrix &x_vars);
   double            Predict(vector &inputs);
   double            Predict(double _input);
   //get properties of OLS model
   ulong             ModelDOF(void) { if(m_error) return 0; else return m_model_dof;}
   ulong             ResidDOF(void) { if(m_error) return 0; else return m_resid_dof;}
   double            Scale(void)  { if(m_error) return EMPTY_VALUE; else return m_scale;    }
   double            Aic(void)    { if(m_error) return EMPTY_VALUE; else return m_aic;      }
   double            Bic(void)    { if(m_error) return EMPTY_VALUE; else return m_bic;    }
   double            Sse(void)    { if(m_error) return EMPTY_VALUE; else return m_sse;    }
   double            Rsqe(void)   { if(m_error) return EMPTY_VALUE; else return m_rsqe;   }
   double            C_tss(void)  { if(m_error) return EMPTY_VALUE; else return m_centeredtss;}
   double            Loglikelihood(void) { if(m_error) return EMPTY_VALUE; return m_llf; }
   vector            Tvalues(void) { if(m_error) return m_m_error.Col(0); return m_tvalues; }
   vector            Residuals(void) { if(m_error) return m_m_error.Col(0); return m_resid; }
   vector            ModelParameters(void) { if(m_error) return m_m_error.Col(0); return m_params; }
   vector            Bse(void) { if(m_error) return m_m_error.Col(0);  return m_bse; }
   matrix            CovarianceMatrix(void) { if(m_error) return m_m_error; return m_cov_params; }
  };

OLS.mqh enthält die Definition der Klasse OLS, die ein Regressionsmodell der gewöhnlichen kleinsten Quadrate darstellt. Die Klasse hat mehrere öffentliche Methoden. Die erste davon ist „Fit()“, die erste Methode, die Nutzer nach der Erstellung einer Instanz dieser Klasse aufrufen sollten. Sie benötigt als Eingabe einen Vektor und eine Matrix. Der Vektor „y_vars“ sollte mit den abhängigen Werten gefüllt werden und „x_vars“ ist die Entwurfsmatrix. „Fit()“ gibt bei erfolgreicher Ausführung true zurück, woraufhin jede andere öffentliche Methode aufgerufen werden kann. Alle diese Methoden geben eine bestimmte Eigenschaft eines berechneten Modells zurück. Diese Eigenschaften sind in der nachstehenden Tabelle zusammengefasst.

Rückgabe-Datentyp	Im Fehlerfall zurückgegebener Wert	Methode	Beschreibung
ulong	0	ModelDOF()	die Freiheitsgrade für ein Modell
ulong	0	ResidDOF()	die Freiheitsgrade für die Residuen eines Modells
double	EMPTY_VALUE	Scale()	Dies ist die Varianz des Fehlerterms, der die Variabilität der abhängigen Variable angibt, die nicht durch die unabhängigen Variablen erklärt wird.
double	EMPTY_VALUE	Aic()	Akaike's Informationskriterien
double	EMPTY_VALUE	Bic()	Die Bayes'schen Informationskriterien
double	EMPTY_VALUE	Sse()	die Summe der quadrierten Fehler des Modells
double	EMPTY_VALUE	Rsqe()	dies ist die R-Quadrat-Metrik des Modells, d. h. das Bestimmtheitsmaß
double	EMPTY_VALUE	C_tss()	dies ist die Gesamtsumme der quadrierten Fehler, die um den Mittelwert zentriert sind
double	EMPTY_VALUE	Loglikelihood()	Die Likelihood-Funktion für das OLS-Modell
vector	‚leerer‘ Vektor	Tvalues()	liefert die t-Statistik für jede Parameterschätzung eines Modells
vector	‚leerer‘ Vektor	Residuals()	die Residuen des Modells, d. h. die Differenz zwischen den vorhergesagten und den tatsächlichen Werten
vector	‚leerer‘ Vektor	Bse()	die Standardfehler der Parameterschätzungen
matrix	‚leere‘ Matrix	CovarianceMatrix()	Matrix, die die Varianzen der Variablen und die Kovarianzen zwischen den Variablen anzeigt

 „Predict()“ hat zwei Überladungen, die sich durch ihre Eingabedatentypen unterscheiden, die entweder ein Vektor oder ein Einzelwert vom Typ double sind. Beide geben eine einzelne Bedingung für neue unabhängige Variable(n) zurück.

Der nächste Teil unserer Implementierung bezieht sich auf die Datei ADF.mqh. Diese Datei enthält eine Sammlung von Funktionsdefinitionen, die sich auf den ADF-Test beziehen. Eine dieser Funktionen wird „adfuller()“ sein. Wir verwenden OLS.mqh für die OLS-Klasse, Math.mqh aus der Standardbibliothek und auch specialfunctions.mqh aus der Alglib-Bibliothek.

//+------------------------------------------------------------------+
//|                                                          ADF.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\specialfunctions.mqh>
#include<OLS.mqh>

Der nächste Teil unserer Implementierung bezieht sich auf die Datei ADF.mqh. Diese Datei enthält eine Sammlung von Funktionsdefinitionen sowie die der CAdf-Klasse. Wir verwenden OLS.mqh für die OLS-Klasse, Math.mqh aus der Standardbibliothek und auch specialfunctions.mqh aus der Alglib-Bibliothek. ADF.mqh beginnt mit der Definition einiger Enumerationen. ENUM_INFO_CRIT stellt die Möglichkeiten dar, die bei der Bestimmung des optimalen Regressionsmodells für eine bestimmte Reihe zur Verfügung stehen. Sie definiert die Kriterien für die Auswahl des richtigen Modells. ENUM_TRIM, ENUM_ORIGINAL, ENUM_HAS_CONST und ENUM_TREND werden bei der Konstruktion einer Gestaltungsmatrix verwendet. 

//+------------------------------------------------------------------+
//| Information criterion                                            |
//+------------------------------------------------------------------+
enum ENUM_INFO_CRIT
  {
   INFO_NONE=0,
   INFO_AIC,
   INFO_BIC
  };
//+------------------------------------------------------------------+
//| Options for  trimming invalid observations                       |
//+------------------------------------------------------------------+
enum ENUM_TRIM
  {
   TRIM_NONE=0,
   TRIM_FORWARD,
   TRIM_BACKWARD,
   TRIM_BOTH
  };
//+------------------------------------------------------------------+
//| options for how to handle original data set                      |
//+------------------------------------------------------------------+

enum ENUM_ORIGINAL
  {
   ORIGINAL_EX=0,
   ORIGINAL_IN,
   ORIGINAL_SEP
  };
//+------------------------------------------------------------------+
//| Constant and trend used in regression model                      |
//+------------------------------------------------------------------+

enum ENUM_TREND
  {
   TREND_NONE=0,
   TREND_CONST_ONLY,
   TREND_LINEAR_ONLY,
   TREND_LINEAR_CONST,
   TREND_QUAD_LINEAR_CONST
  };
//+------------------------------------------------------------------+
//| Options for how to handle existing constants                     |
//+------------------------------------------------------------------+

enum ENUM_HAS_CONST
  {
   HAS_CONST_RAISE=0,
   HAS_CONST_SKIP,
   HAS_CONST_ADD
  };

Die Methode „Adfuller()“ von CAdf gibt einen booleschen Wert zurück, der die erfolgreiche Durchführung des Tests angibt und NICHT DIE STATIONARITÄT einer SERIE. Wenn false zurückgegeben wird, muss ein Fehler aufgetreten sein. Alle Fehler werden von ausführlichen Meldungen begleitet, die im Journal des Terminals ausgegeben werden. Als Eingabe dient ein Array mit einer zu analysierenden Reihe.  Andere Argumente für die Funktion sind optional. In den meisten Fällen müssen sich die Nutzer nicht mit diesen Parametern befassen. Der Aufruf der Funktion mit den oben genannten Parametern sollte ausreichen.

//+---------------------------------------------------------------------+
//|Class CAdf                                                           |
//|   encapsulates the the Augmented Dickey Fuller Test for Stationarity|
//+---------------------------------------------------------------------+

class CAdf
{
 private:
  double m_adf_stat,  //adf statistic
         m_bestic,    //optimal bic or aic
         m_pvalue;    //p-value
  ulong  m_usedlag;   //lag used for optimal reg model
  vector m_critvals;  //estimated critical values
  OLS    *m_ols;      //internal ordinary least squares reg model
   // private methods
 bool   gridsearch(vector &LHS, matrix &RHS, ulong f_lag, ulong l_lag,ENUM_INFO_CRIT crit, double &b_ic, ulong &best_lag);
 bool   lagmat(matrix &in,matrix &out[],ulong mlag,ENUM_TRIM trim=TRIM_BOTH,ENUM_ORIGINAL original=ORIGINAL_IN);
 bool   prepare_lhs_rhs(vector &lhs, matrix &rhs, double &in[], double &in_diff[],ulong lag);
 
 
 public:
  CAdf(void);
  ~CAdf(void);
  
 bool Adfuller(double &array[],ulong max_lag = 0,ENUM_TREND trend = TREND_CONST_ONLY, ENUM_INFO_CRIT autolag=INFO_AIC);
 vector CriticalValues(void) {  return m_critvals; }
 double AdfStatistic(void)   {  return m_adf_stat; }
 double Pvalue(void)         {  return m_pvalue;   }
};

„max_lag“ legt die maximale Anzahl der Verzögerungen (lags) des Regressionsmodells fest. „trend“ ist eine Enumeration, die die Spezifikation des Trends und der konstanten Konfiguration des Regressionsmodells ermöglicht. „autolag“ legt fest, welche Metrik verwendet wird, um das optimale Modell auszuwählen, das die Eingabereihen am besten beschreibt. Im Rahmen von „Adfuller()“ werden zunächst die Funktionsparameter überprüft, bevor sie zur Konstruktion der abhängigen und unabhängigen Variablen eines Regressionsmodells verwendet werden.

Es werden mehrere Varianten dieser anfänglichen Entwurfsmatrix ausprobiert, um festzustellen, welche am besten zu den Eingangsreihen passt. Die Kriterien für die Auswahl des besten Modells hängen vom Wert des Parameters „autolag“ ab. Die Suche wird von der Funktion „gridsearch()“ durchgeführt.

Sobald das beste Modell gefunden ist, wird die Verzögerungseigenschaft dieses Modells, die sich auf die Anzahl der in der ursprünglichen Entwurfsmatrix enthaltenen Spalten bezieht, zur Definition des optimalen Modells verwendet. Dessen Parameter werden verwendet, um die Stationarität der Reihe zu schätzen. Die erste t-Statistik des optimalen OLS-Modells definiert die ADF-Statistik des ADF-Tests. Der p-Wert wird mit der Funktion „mackinnop()“ berechnet. Der Aufruf der CAdf-Methode „Pvalue()“ liefert den entsprechenden p-Wert.

//+----------------------------------------------------------------------+
//| calculates MacKinnon's approximate p-value for a given test statistic|
//+----------------------------------------------------------------------+
double mackinnonp(double teststat, ENUM_TREND trend = TREND_CONST_ONLY,ulong nseries = 1, uint lags =0)
  {
   vector small_scaling =  {1, 1, 1e-2};
   vector large_scaling =  {1, 1e-1, 1e-1, 1e-2};

   double tau_star_nc []= {-1.04, -1.53, -2.68, -3.09, -3.07, -3.77};
   double tau_min_nc []= {-19.04, -19.62, -21.21, -23.25, -21.63, -25.74};
   double tau_max_nc []= {double("inf"), 1.51, 0.86, 0.88, 1.05, 1.24};
   double tau_star_c []= {-1.61, -2.62, -3.13, -3.47, -3.78, -3.93};
   double tau_min_c []= {-18.83, -18.86, -23.48, -28.07, -25.96, -23.27};
   double tau_max_c []= {2.74, 0.92, 0.55, 0.61, 0.79, 1};
   double tau_star_ct []= {-2.89, -3.19, -3.50, -3.65, -3.80, -4.36};
   double tau_min_ct []= {-16.18, -21.15, -25.37, -26.63, -26.53, -26.18};
   double tau_max_ct []= {0.7, 0.63, 0.71, 0.93, 1.19, 1.42};
   double tau_star_ctt []= {-3.21, -3.51, -3.81, -3.83, -4.12, -4.63};
   double tau_min_ctt []= {-17.17, -21.1, -24.33, -24.03, -24.33, -28.22};
   double tau_max_ctt []= {0.54, 0.79, 1.08, 1.43, 3.49, 1.92};

   double tau_nc_smallp [][3]=
     {
        {0.6344, 1.2378, 3.2496},
        {1.9129, 1.3857, 3.5322},
        {2.7648, 1.4502, 3.4186},
        {3.4336, 1.4835, 3.19},
        {4.0999, 1.5533, 3.59},
        {4.5388, 1.5344, 2.9807}
     };

   double tau_c_smallp [][3]=
     {
        {2.1659, 1.4412, 3.8269},
        {2.92, 1.5012, 3.9796},
        {3.4699, 1.4856, 3.164},
        {3.9673, 1.4777, 2.6315},
        {4.5509, 1.5338, 2.9545},
        {5.1399, 1.6036, 3.4445}
     };

   double tau_ct_smallp [][3]=
     {
        {3.2512, 1.6047, 4.9588},
        {3.6646, 1.5419, 3.6448},
        {4.0983, 1.5173, 2.9898},
        {4.5844, 1.5338, 2.8796},
        {5.0722, 1.5634, 2.9472},
        {5.53, 1.5914, 3.0392}
     };

   double tau_ctt_smallp [][3]=
     {
        {4.0003, 1.658, 4.8288},
        {4.3534, 1.6016, 3.7947},
        {4.7343, 1.5768, 3.2396},
        {5.214, 1.6077, 3.3449},
        {5.6481, 1.6274, 3.3455},
        {5.9296, 1.5929, 2.8223}
     };



   double tau_nc_largep [][4]=
     {
        {0.4797, 9.3557, -0.6999, 3.3066},
        {1.5578, 8.558, -2.083, -3.3549},
        {2.2268, 6.8093, -3.2362, -5.4448},
        {2.7654, 6.4502, -3.0811, -4.4946},
        {3.2684, 6.8051, -2.6778, -3.4972},
        {3.7268, 7.167, -2.3648, -2.8288}
     };

   double tau_c_largep [][4]=
     {
        {1.7339, 9.3202, -1.2745, -1.0368},
        {2.1945, 6.4695, -2.9198, -4.2377},
        {2.5893, 4.5168, -3.6529, -5.0074},
        {3.0387, 4.5452, -3.3666, -4.1921},
        {3.5049, 5.2098, -2.9158, -3.3468},
        {3.9489, 5.8933, -2.5359, -2.721}
     };

   double tau_ct_largep [][4]=
     {
        {2.5261, 6.1654, -3.7956, -6.0285},
        {2.85, 5.272, -3.6622, -5.1695},
        {3.221, 5.255, -3.2685, -4.1501},
        {3.652, 5.9758, -2.7483, -3.2081},
        {4.0712, 6.6428, -2.3464, -2.546},
        {4.4735, 7.1757, -2.0681, -2.1196}
     };

   double tau_ctt_largep [][4]=
     {
        {3.0778, 4.9529, -4.1477, -5.9359},
        {3.4713, 5.967, -3.2507, -4.2286},
        {3.8637, 6.7852, -2.6286, -3.1381},
        {4.2736, 7.6199, -2.1534, -2.4026},
        {4.6679, 8.2618, -1.822, -1.9147},
        {5.0009, 8.3735, -1.6994, -1.6928}
     };


   vector maxstat,minstat,starstat;
   matrix tau_smallps, tau_largeps;

   switch(trend)
     {
      case TREND_NONE:
         if(!maxstat.Assign(tau_max_nc) ||
            !minstat.Assign(tau_min_nc) ||
            !starstat.Assign(tau_star_nc)||
            !tau_smallps.Assign(tau_nc_smallp)||
            !tau_largeps.Assign(tau_nc_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_CONST_ONLY:
         if(!maxstat.Assign(tau_max_c) ||
            !minstat.Assign(tau_min_c) ||
            !starstat.Assign(tau_star_c)||
            !tau_smallps.Assign(tau_c_smallp)||
            !tau_largeps.Assign(tau_c_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ct) ||
            !minstat.Assign(tau_min_ct) ||
            !starstat.Assign(tau_star_ct)||
            !tau_smallps.Assign(tau_ct_smallp)||
            !tau_largeps.Assign(tau_ct_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      case TREND_QUAD_LINEAR_CONST:
         if(!maxstat.Assign(tau_max_ctt) ||
            !minstat.Assign(tau_min_ctt) ||
            !starstat.Assign(tau_star_ctt)||
            !tau_smallps.Assign(tau_ctt_smallp)||
            !tau_largeps.Assign(tau_ctt_largep))
           {
            Print("assignment error :", GetLastError());
            return double("inf");
           }
         else
            break;
      default:
         Print(__FUNCTION__," Error invalid input for trend argument");
         return double("nan");
     }

   if(teststat>maxstat[nseries-1])
      return 1.0;
   else
      if(teststat<minstat[nseries-1])
         return 0.0;


   vector tau_coef;

   if(teststat<=starstat[nseries-1])
      tau_coef = small_scaling*(tau_smallps.Row(nseries-1));
   else
      tau_coef = large_scaling*(tau_largeps.Row(nseries-1));


   double rv,tau[];

   ArrayResize(tau,int(tau_coef.Size()));

   for(ulong i=0; i<tau_coef.Size(); i++)
      tau[i]=tau_coef[tau_coef.Size()-1-i];

   rv=polyval(tau,teststat);

   return CNormalDistr::NormalCDF(rv);
  }

Die kritischen Werte werden mit „mackinnoncrit()“ berechnet. Deren Ergebnisse können über die CAdf-Methode „CriticalValues()“ abgerufen werden.

//+------------------------------------------------------------------+
//|Computes critical values                                          |
//+------------------------------------------------------------------+
vector mackinnoncrit(ulong nseries = 1,ENUM_TREND trend = TREND_CONST_ONLY, ulong num_obs=ULONG_MAX)
  {
   matrix tau_nc_2010 [] = {{
           {-2.56574, -2.2358, -3.627, 0},  // N [] = 1
           {-1.94100, -0.2686, -3.365, 31.223},
           {-1.61682, 0.2656, -2.714, 25.364}
        }
     };

   matrix tau_c_2010 [] =
     {
        {  {-3.43035, -6.5393, -16.786, -79.433},  // N [] = 1, 1%
           {-2.86154, -2.8903, -4.234, -40.040},   // 5 %
           {-2.56677, -1.5384, -2.809, 0}
        },        // 10 %
        {  {-3.89644, -10.9519, -33.527, 0},       // N [] = 2
           {-3.33613, -6.1101, -6.823, 0},
           {-3.04445, -4.2412, -2.720, 0}
        },
        {  {-4.29374, -14.4354, -33.195, 47.433},  // N [] = 3
           {-3.74066, -8.5632, -10.852, 27.982},
           {-3.45218, -6.2143, -3.718, 0}
        },
        {  {-4.64332, -18.1031, -37.972, 0},       // N [] = 4
           {-4.09600, -11.2349, -11.175, 0},
           {-3.81020, -8.3931, -4.137, 0}
        },
        {  {-4.95756, -21.8883, -45.142, 0},       // N [] = 5
           {-4.41519, -14.0405, -12.575, 0},
           {-4.13157, -10.7417, -3.784, 0}
        },
        {  {-5.24568, -25.6688, -57.737, 88.639},  // N [] = 6
           {-4.70693, -16.9178, -17.492, 60.007},
           {-4.42501, -13.1875, -5.104, 27.877}
        },
        {  {-5.51233, -29.5760, -69.398, 164.295},  // N [] = 7
           {-4.97684, -19.9021, -22.045, 110.761},
           {-4.69648, -15.7315, -5.104, 27.877}
        },
        {  {-5.76202, -33.5258, -82.189, 256.289},  // N [] = 8
           {-5.22924, -23.0023, -24.646, 144.479},
           {-4.95007, -18.3959, -7.344, 94.872}
        },
        {  {-5.99742, -37.6572, -87.365, 248.316},  // N [] = 9
           {-5.46697, -26.2057, -26.627, 176.382},
           {-5.18897, -21.1377, -9.484, 172.704}
        },
        {  {-6.22103, -41.7154, -102.680, 389.33},  // N [] = 10
           {-5.69244, -29.4521, -30.994, 251.016},
           {-5.41533, -24.0006, -7.514, 163.049}
        },
        {  {-6.43377, -46.0084, -106.809, 352.752},  // N [] = 11
           {-5.90714, -32.8336, -30.275, 249.994},
           {-5.63086, -26.9693, -4.083, 151.427}
        },
        {  {-6.63790, -50.2095, -124.156, 579.622},  // N [] = 12
           {-6.11279, -36.2681, -32.505, 314.802},
           {-5.83724, -29.9864, -2.686, 184.116}
        }
     };

   matrix tau_ct_2010 [] =
     {
        {  {-3.95877, -9.0531, -28.428, -134.155},   // N [] = 1
           {-3.41049, -4.3904, -9.036, -45.374},
           {-3.12705, -2.5856, -3.925, -22.380}
        },
        {  {-4.32762, -15.4387, -35.679, 0},         // N [] = 2
           {-3.78057, -9.5106, -12.074, 0},
           {-3.49631, -7.0815, -7.538, 21.892}
        },
        {  {-4.66305, -18.7688, -49.793, 104.244},   // N [] = 3
           {-4.11890, -11.8922, -19.031, 77.332},
           {-3.83511, -9.0723, -8.504, 35.403}
        },
        {  {-4.96940, -22.4694, -52.599, 51.314},    // N [] = 4
           {-4.42871, -14.5876, -18.228, 39.647},
           {-4.14633, -11.2500, -9.873, 54.109}
        },
        {  {-5.25276, -26.2183, -59.631, 50.646},    // N [] = 5
           {-4.71537, -17.3569, -22.660, 91.359},
           {-4.43422, -13.6078, -10.238, 76.781}
        },
        {  {-5.51727, -29.9760, -75.222, 202.253},   // N [] = 6
           {-4.98228, -20.3050, -25.224, 132.03},
           {-4.70233, -16.1253, -9.836, 94.272}
        },
        {  {-5.76537, -33.9165, -84.312, 245.394},   // N [] = 7
           {-5.23299, -23.3328, -28.955, 182.342},
           {-4.95405, -18.7352, -10.168, 120.575}
        },
        {  {-6.00003, -37.8892, -96.428, 335.92},    // N [] = 8
           {-5.46971, -26.4771, -31.034, 220.165},
           {-5.19183, -21.4328, -10.726, 157.955}
        },
        {  {-6.22288, -41.9496, -109.881, 466.068},  // N [] = 9
           {-5.69447, -29.7152, -33.784, 273.002},
           {-5.41738, -24.2882, -8.584, 169.891}
        },
        {  {-6.43551, -46.1151, -120.814, 566.823},  // N [] = 10
           {-5.90887, -33.0251, -37.208, 346.189},
           {-5.63255, -27.2042, -6.792, 177.666}
        },
        {  {-6.63894, -50.4287, -128.997, 642.781},  // N [] = 11
           {-6.11404, -36.4610, -36.246, 348.554},
           {-5.83850, -30.1995, -5.163, 210.338}
        },
        {  {-6.83488, -54.7119, -139.800, 736.376},  // N [] = 12
           {-6.31127, -39.9676, -37.021, 406.051},
           {-6.03650, -33.2381, -6.606, 317.776}
        }
     };

   matrix tau_ctt_2010 [] =
     {
        {  {-4.37113, -11.5882, -35.819, -334.047},  // N [] = 1
           {-3.83239, -5.9057, -12.490, -118.284},
           {-3.55326, -3.6596, -5.293, -63.559}
        },
        {  {-4.69276, -20.2284, -64.919, 88.884},    // N [] =2
           {-4.15387, -13.3114, -28.402, 72.741},
           {-3.87346, -10.4637, -17.408, 66.313}
        },
        {  {-4.99071, -23.5873, -76.924, 184.782},   // N [] = 3
           {-4.45311, -15.7732, -32.316, 122.705},
           {-4.17280, -12.4909, -17.912, 83.285}
        },
        {  {-5.26780, -27.2836, -78.971, 137.871},   // N [] = 4
           {-4.73244, -18.4833, -31.875, 111.817},
           {-4.45268, -14.7199, -17.969, 101.92}
        },
        {  {-5.52826, -30.9051, -92.490, 248.096},   // N [] = 5
           {-4.99491, -21.2360, -37.685, 194.208},
           {-4.71587, -17.0820, -18.631, 136.672}
        },
        {  {-5.77379, -34.7010, -105.937, 393.991},  // N [] = 6
           {-5.24217, -24.2177, -39.153, 232.528},
           {-4.96397, -19.6064, -18.858, 174.919}
        },
        {  {-6.00609, -38.7383, -108.605, 365.208},  // N [] = 7
           {-5.47664, -27.3005, -39.498, 246.918},
           {-5.19921, -22.2617, -17.910, 208.494}
        },
        {  {-6.22758, -42.7154, -119.622, 421.395},  // N [] = 8
           {-5.69983, -30.4365, -44.300, 345.48},
           {-5.42320, -24.9686, -19.688, 274.462}
        },
        {  {-6.43933, -46.7581, -136.691, 651.38},   // N [] = 9
           {-5.91298, -33.7584, -42.686, 346.629},
           {-5.63704, -27.8965, -13.880, 236.975}
        },
        {  {-6.64235, -50.9783, -145.462, 752.228},  // N [] = 10
           {-6.11753, -37.056, -48.719, 473.905},
           {-5.84215, -30.8119, -14.938, 316.006}
        },
        {  {-6.83743, -55.2861, -152.651, 792.577},  // N [] = 11
           {-6.31396, -40.5507, -46.771, 487.185},
           {-6.03921, -33.8950, -9.122, 285.164}
        },
        {  {-7.02582, -59.6037, -166.368, 989.879},  // N [] = 12
           {-6.50353, -44.0797, -47.242, 543.889},
           {-6.22941, -36.9673, -10.868, 418.414}
        }
     };

   vector ret_vector = {0,0,0};

   switch(trend)
     {
      case TREND_CONST_ONLY:
         process(tau_c_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_NONE:
         process(tau_nc_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_LINEAR_CONST:
         process(tau_ct_2010,ret_vector,num_obs,nseries);
         break;
      case TREND_QUAD_LINEAR_CONST:
         process(tau_ctt_2010,ret_vector,num_obs,nseries);
         break;
      default:
         Print("Invalid input for trend argument");
         return ret_vector;
     }

   return ret_vector;
  }

Prüfung und Validierung

Um zu überprüfen, ob unsere Implementierung korrekt funktioniert, führen wir zunächst einen ADF-Test in Python mit einer Zufallsreihe durch. Anschließend werden wir den ADF-Test für dieselbe Serie in Metatrader 5 durchführen und die Ergebnisse vergleichen.

Der Code für den ADF-Test in Python ist unten aufgeführt.

import numpy as np
from statsmodels.tsa.stattools import adfuller

#initialize array with 100 elements
x = np.array([0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
              0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
              0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
              0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
              0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
              0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
              0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
              0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
              0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
              0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
              0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
              0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
              0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
              0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
              0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
              0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
              0.20684364,0.29630613,0.65178447,0.86559185])
   
#perform ADF test on array 
result = adfuller(x)

#print ADF statistic and p-value
print(f"ADF statistic: {result[0]}, p-value:{result[1]}")

#print critical values
print(f"Critical values:{result[4]}")
   

Als Nächstes führen wir die MQL5-Version des ADF-Tests mit demselben Array aus. Der Programmcode des Skripts ist unten dargestellt.

//+------------------------------------------------------------------+
//|                                                     ADF_test.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<ADF.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---series
   double rand_array[] =
     {
      0.97841555,0.31931195,0.68205832,0.56256707,0.05741117,0.30310286,
      0.13354023,0.61382247,0.20699517,0.61969826,0.55718307,0.90422809,
      0.24220947,0.08719106,0.26714434,0.39439596,0.93919107,0.07756139,
      0.53188798,0.5074042,0.40468052,0.41235659,0.79233157,0.58948591,
      0.22049794,0.68278894,0.09500558,0.40421058,0.9971231,0.29665678,
      0.08254796,0.8089725,0.61434576,0.97610604,0.84084868,0.8034953,
      0.765576,0.25014613,0.16268394,0.34259495,0.40085009,0.8416158,
      0.6321962,0.45165205,0.12209775,0.40556958,0.96253644,0.30619429,
      0.70573114,0.51574979,0.90168104,0.80757639,0.94321618,0.58849563,
      0.38905617,0.04574506,0.63134219,0.89198262,0.24102367,0.45749333,
      0.76804682,0.50868223,0.91132151,0.7372344,0.32551467,0.27799709,
      0.04059095,0.86024797,0.74600612,0.01264258,0.89364963,0.99373472,
      0.36177673,0.47173929,0.15124127,0.77354455,0.45131917,0.27258213,
      0.69618127,0.35105122,0.1261404,0.21705172,0.88979093,0.97598448,
      0.03787156,0.54034132,0.58336702,0.61701685,0.11673483,0.99940389,
      0.99371688,0.04428256,0.00239077,0.34609507,0.57588045,0.20222325,
      0.20684364,0.29630613,0.65178447,0.86559185
     };

//---variables that will be used to store test results
   CAdf adf;
//--- Do ADF test
   if(adf.Adfuller(rand_array))
      Print("ADF test statistic: ", adf.AdfStatistic(), " P-value:", adf.Pvalue(),"\nCritical values \n",adf.CriticalValues());
   else
      Print("ADF test failed");
  }
//+------------------------------------------------------------------+

Wenn wir zunächst das Python-Skript ausführen, erhalten wir:

LD      0       18:30:22.912    Test_adfuller (NFLX_us,Daily)   ADF statistic: -8.495443215534635, p-value:1.2796318143567197e-13
GJ      0       18:30:22.913    Test_adfuller (NFLX_us,Daily)   Critical values:{'1%': -3.4989097606014496, '5%': -2.891516256916761, '10%': -2.5827604414827157}

Und dann als nächstes das MetaTrader 5 Skript. Wir können sehen, die Ergebnisse sind gleich.

DO      0       18:30:48.460    ADF_test (NFLX_us,D1)   ADF test statistic: -8.495443215534634 P-value:1.2796318143567197e-13
ND      0       18:30:48.460    ADF_test (NFLX_us,D1)   Critical values 
OL      0       18:30:48.460    ADF_test (NFLX_us,D1)   [-3.49890976060145,-2.891516256916761,-2.582760441482716]

Kointegration

Korrelation und Kointegration sind statistische Konzepte, die zur Messung von Beziehungen zwischen Variablen, insbesondere im Zusammenhang mit Zeitreihendaten, verwendet werden. Beide messen zwar Beziehungen, dienen aber unterschiedlichen Zwecken und werden in verschiedenen Szenarien eingesetzt. Die Korrelation ist das statistische Maß für die Stärke und Richtung der linearen Beziehung zwischen zwei Variablen.

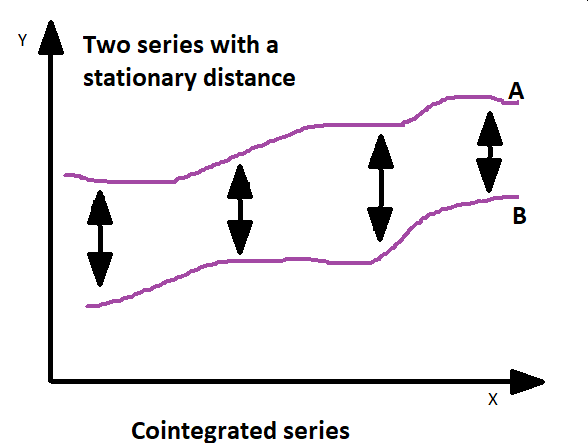
Die Kointegration hingegen befasst sich mit der Beziehung zwischen nicht-stationären Zeitreihenvariablen, die ein langfristiges Gleichgewicht oder eine stetige Beziehung aufweisen. Einfacher ausgedrückt: Es wird ermittelt, ob es eine Kombination von zwei oder mehr nicht-stationären Variablen gibt, die bei gemeinsamer Betrachtung eine stabile, langfristige Beziehung aufweisen. Die Kointegration ist nützlich, um Paare von Variablen zu ermitteln, die sich trotz kurzfristiger Schwankungen im Laufe der Zeit gemeinsam bewegen. Dies bedeutet, dass die Variablen langfristig miteinander verbunden sind, was es ermöglicht, diese Beziehung für Handelsstrategien oder Modellierung zu nutzen.

Die Kointegration wird in der Regel mit statistischen Tests wie dem Engle-Granger-Test oder dem Johansen-Test bewertet. Mit diesen Tests wird geprüft, ob eine lineare Kombination von nicht-stationären Variablen eine stationäre Reihe ergibt, die auf eine langfristige Beziehung hinweist. Der Engle-Granger-Test ist ein zweistufiges Verfahren zur Prüfung auf Kointegration zwischen zwei Variablen in einem Zeitreihenumfeld. Sie beinhaltet die Schätzung eines Regressionsmodells und die anschließende Prüfung der Residuen, um festzustellen, ob eine Kointegration vorliegt. Wenn sich die Residuen des Regressionsmodells als stationär erweisen, deutet dies auf eine Kointegration zwischen den beiden Variablen hin. In diesem Fall bedeutet dies, dass eine lineare Kombination der Variablen stationär ist, obwohl die Variablen einzeln nicht stationär sind.

Der Engle-Granger-Test ist insofern begrenzt, als er nicht mehrere Sequenzen gleichzeitig verarbeiten kann. Diese Einschränkung wird durch den Johansen-Test behoben. Dabei handelt es sich im Wesentlichen um eine Erweiterung des Engle-Granger-Ansatzes zur Prüfung auf Kointegration zwischen mehreren Reihen in einem vektorautoregressiven Modell. In diesem Artikel werden wir den Johansen-Test nicht untersuchen, da wir uns auf zwei Reihen beschränken.

CointegrationTest.mqh enthält die Klasse CCoint. Es implementiert den erweiterten Engle-Granger-Test mit Hilfe der Klasse CAdf. Der Test wird durch den Aufruf der Methode „Aeg()“ von CCoint durchgeführt. Es sind zwei Eingabefelder erforderlich, die die zu prüfenden Reihen enthalten. Die optionalen Eingabeparameter „trend“, „max_lag“ und „autolag“ entsprechen den Parametern der Methode „Adfuller()“ in CAdf. Auch hier sollten die Standardwerte für die meisten Tests ausreichend sein. Wie im nächsten Abschnitt gezeigt wird.  Die Ergebnisse des Kointegrationstests werden durch den Aufruf von drei Methoden von CCoint erzielt. Die erste „CointStatistic“ liefert die ADF-Statistik aus dem internen ADF-Test. „CriticalValues()“ gibt einen Vektor mit den kritischen Werten des Tests zurück. Der p-Wert kann durch Aufruf von „P-Wert()“ ermittelt werden.

//+------------------------------------------------------------------+
//|                                            CointegrationTest.mqh |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include<ADF.mqh>

//+------------------------------------------------------------------+
//|Class CCoint                                                      |
//|    implements cointegration test of two series                   |
//+------------------------------------------------------------------+
class CCoint
{
 private:
  double m_coint_stat;       //ADF test statistic
  double m_coint_pvalue;     //cointegration p-value
  vector m_coint_critvalues; //Cointegration critical values
  CAdf   *m_adf;             //CAdf object pointer
 public:
  CCoint(void);
  ~CCoint(void);
  
  bool Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC);
  
  double CointStatistic(void){ return m_coint_stat; }
  double Pvalue(void)        { return m_coint_pvalue;}
  vector CriticalValues(void){ return m_coint_critvalues;}
};
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CCoint::CCoint(void)
{
 m_adf = new CAdf();
 
 m_coint_critvalues = vector::Zeros(3);
 
 m_coint_stat=m_coint_pvalue=EMPTY_VALUE;
}
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CCoint::~CCoint(void)
{
 if(CheckPointer(m_adf)==POINTER_DYNAMIC)
     delete m_adf;
}
//+------------------------------------------------------------------+
//| Test for cointegration                                           |
//+------------------------------------------------------------------+
bool CCoint::Aeg(double &in_one[],double &in_two[],ENUM_TREND trend = TREND_CONST_ONLY,ulong max_lag=0,ENUM_INFO_CRIT autolag=INFO_AIC)
  {
//---  
   if(CheckPointer(m_adf)==POINTER_INVALID)
    {
     Print("Critical Internal error: Invalid CAdf pointer");
     return false;
    }
//---    
   if(in_one.Size()<1 || in_two.Size()<1 || in_one.Size()!=in_two.Size())
     {
      Print(__FUNCTION__," Invalid input for one or both arrays");
      return false;
     }

   vector y1,temp;
   matrix y2;

   if(!y1.Assign(in_one) || !temp.Assign(in_two) || !y2.Resize(temp.Size(),1) || !y2.Col(temp,0))
     {
      Print(__FUNCTION__," Assignment error: ", GetLastError());
      return false;
     }


   ulong obs,kvars=1;
   obs = y2.Rows();
   kvars++;
   matrix xx;

   if(trend==TREND_NONE)
     {
      if(!xx.Copy(y2))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }
     }
   else
    if(!addtrend(y2,xx,trend,false))
        {
         Print(__FUNCTION__," Assignment error: ", GetLastError());
         return false;
        }

   OLS ols;

   if(!ols.Fit(y1,xx))
      return false;

   if(ols.Rsqe()< 1 - 100*SQRTEPS)
     {
      double resid[];

      vector resd = ols.Residuals();

      ArrayResize(resid,int(resd.Size()));

      for(uint i = 0; i<resid.Size(); i++)
         resid[i]=resd[i];

      if(!m_adf.Adfuller(resid,max_lag,TREND_NONE,autolag))
         return false;

      m_coint_stat = m_adf.AdfStatistic();
     }
   else
     {
      Print("They are (almost) perfectly collinear.\nCointegration test is not reliable in this case");
      m_coint_stat=double("nan");
     }

   if(trend==TREND_NONE)
      m_coint_critvalues.Fill(double("nan"));
   else
      m_coint_critvalues = mackinnoncrit(kvars,trend,obs-1);

   m_coint_pvalue = mackinnonp(m_coint_stat,trend,kvars);

   return true;
  }    

Testsymbole für Kointegration

Für die letzte Demonstration werden wir ein MQL5-Skript erstellen, das CCoint verwendet, um eine Liste von Symbolen auf Kointegration zu testen. Die Nutzer geben eine Liste von Symbolen ein, die durch Kommas getrennt sind. Legen Sie das Startdatum und die Dauer der zu untersuchenden Schlusskurse fest. Mit „ConfidenceLevel“ kann der Nutzer das gewünschte Signifikanzniveau auswählen. Dies bestimmt den kritischen Wert, der für das Endergebnis mit der ADF-Statistik verglichen wird.

//+------------------------------------------------------------------+
//|                                    SymbolCointegrationTester.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <CointegrationTest.mqh>
//+------------------------------------------------------------------+
//| enumeration maps to confidence levels of 99%,95%, and 90%        |
//+------------------------------------------------------------------+
enum ENUM_CONFIDENCE_LEVEL
  {
   CONF_99=0,//99%
   CONF_95,//95%
   CONF_90 //90%
  };
//--- input parameters
input string   Symbols = "FB_us,GOOG_us,MSFT_us,NFLX_us,NVDA_us,AAPL_us,TSLA_us";//Comma separated list of symbols to test
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input datetime StartDate=D'2022.01.01 00:00:01';
input int Size = 250;//History length
input ENUM_CONFIDENCE_LEVEL ConfidenceLevel=CONF_90;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---Check Size input value
   if(Size<100)
     {
      Print("Invalid input for Size");
      return;
     }
//---array for symbols
   string symbols[];
//---process list of symbols from user input
   int num_symbols = StringSplit(Symbols,StringGetCharacter(",",0),symbols);
//---incase list contains ending comma
   if(symbols[num_symbols-1]=="")
      num_symbols--;

//---in case there are less than two symbols specified
   if(num_symbols<2)
     {
      Print("Invalid input. Please list at least two symbols");
      return;
     }
//---output matrix of indices
   matrix sym_combos;
//---fill sym_combos with index values of symbols array
   PairedCombinations(symbols,sym_combos,num_symbols);
//---price arrays for pair of symbols
   double symA_prices [], symB_prices[];
//---output vectors holding results of cointegration test
   vector stats, critvals;
//---symbol pairs and result output
   string symA,symB,result;
//---CCoint object
   CCoint coint;
//---loop through all paired combinations from list
   for(ulong i=0; i<sym_combos.Rows(); i++)
     {
      //--- get symbol pair for current combination
      symA = symbols[int(sym_combos[i][0])];
      symB = symbols[int(sym_combos[i][1])];
      //--- get prices for the pair of symbols
      if(CopyClose(symA,TimeFrame,StartDate,Size,symA_prices)<Size||
         CopyClose(symB,TimeFrame,StartDate,Size,symB_prices)<Size)
        {
         Print("Failed to copy close prices ", ::GetLastError());
         return;
        }
      //--- test the pair for cointegreation
      if(!coint.Aeg(symA_prices,symB_prices))
        {
         Print("Cointegration test failed ", ::GetLastError());
         return;
        }
      //---
      vector critvals = coint.CriticalValues();
      //--- prepare results output for a test
      if(coint.CointStatistic()<critvals[ConfidenceLevel])
         result="likely cointegrated.";
      else
         result="likely not cointegrated.";
      //--- output the result from cointegration test
      Print(symA," and ",symB, " are ", result);
     }
  }
//+------------------------------------------------------------------+
//| Combinations: generates paired combinations                      |
//+------------------------------------------------------------------+
bool PairedCombinations(string &in[], matrix &out,int count = 0)
  {
//---check input array
   if(in.Size()<1)
     {
      Print(__FUNCTION__," input array is empty");
      return false;
     }
//---set value for upto equal to the number of elements that should be
//---considered in the input array
   int upto = (count>1 && count<ArraySize(in))?count:ArraySize(in);
//--- calculate the number of rows equivalent to number of combinations
   ulong rows = ulong(MathFactorial(upto)/(MathFactorial(2)*MathFactorial(upto-2)));
//---resize output matrix accordingly
   out.Resize(rows,2);
//---fill output matrix with indexes of input array
   for(uint i=0,z=0; i<in.Size(); i++)
     {
      for(uint k = i+1; k<in.Size(); k++,z++)
        {
         out[z][0]=i;
         out[z][1]=k;
        }
     }
//---return
   return true;
  }
//+------------------------------------------------------------------+

In unserem Beispiel werden wir die Symbole Google, Facebook, Microsoft, NetFlix, Nvidia, Apple und Tesla testen. Die Ergebnisse der Ausführung des Skripts sind unten dargestellt.

HN      0       18:37:31.239    SymbolCointegrationTester (NFLX_us,D1)  FB_us and GOOG_us are likely not cointegrated.
PQ      0       18:37:31.280    SymbolCointegrationTester (NFLX_us,D1)  FB_us and MSFT_us are likely not cointegrated.
IE      0       18:37:31.322    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NFLX_us are likely not cointegrated.
MG      0       18:37:31.365    SymbolCointegrationTester (NFLX_us,D1)  FB_us and NVDA_us are likely not cointegrated.
PH      0       18:37:31.411    SymbolCointegrationTester (NFLX_us,D1)  FB_us and AAPL_us are likely not cointegrated.
NL      0       18:37:31.453    SymbolCointegrationTester (NFLX_us,D1)  FB_us and TSLA_us are likely not cointegrated.
EO      0       18:37:31.496    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and MSFT_us are likely not cointegrated.
ES      0       18:37:31.540    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NFLX_us are likely not cointegrated.
FE      0       18:37:31.582    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and NVDA_us are likely not cointegrated.
CF      0       18:37:31.623    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and AAPL_us are likely not cointegrated.
EJ      0       18:37:31.665    SymbolCointegrationTester (NFLX_us,D1)  GOOG_us and TSLA_us are likely not cointegrated.
HM      0       18:37:31.705    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NFLX_us are likely not cointegrated.
RN      0       18:37:31.744    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and NVDA_us are likely not cointegrated.
LP      0       18:37:31.785    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and AAPL_us are likely not cointegrated.
OD      0       18:37:31.825    SymbolCointegrationTester (NFLX_us,D1)  MSFT_us and TSLA_us are likely not cointegrated.
IG      0       18:37:31.866    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and NVDA_us are likely not cointegrated.
QI      0       18:37:31.906    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and AAPL_us are likely not cointegrated.
FP      0       18:37:31.946    SymbolCointegrationTester (NFLX_us,D1)  NFLX_us and TSLA_us are likely cointegrated.
EO      0       18:37:31.987    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and AAPL_us are likely not cointegrated.
RS      0       18:37:32.026    SymbolCointegrationTester (NFLX_us,D1)  NVDA_us and TSLA_us are likely not cointegrated.
DE      0       18:37:32.072    SymbolCointegrationTester (NFLX_us,D1)  AAPL_us and TSLA_us are likely not cointegrated.

Sie zeigen, dass NetFlix und Tesla bei einem Konfidenzniveau von 90 % wahrscheinlich kointegriert sind.

Es folgt der Code für die Durchführung desselben Tests in Python, zusammen mit den Ergebnissen.

"""
 Script demonstrates use of coint() from statsmodels
 to test symbols for cointegration
"""
# imports 
from statsmodels.tsa.stattools import coint
from itertools import combinations
from datetime import datetime
import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import pytz

#initialize connection to mt5
if not mt5.initialize():
    print("initialize() failed ")
    mt5.shutdown()
 
#set up timezone infomation   
tz=pytz.timezone("Etc/UTC")

#use time zone to set correct date for history data extraction
startdate = datetime(2022,1,1,hour=0,minute=0,second=1,tzinfo=tz)

#list the symbols 
Symbols = ["FB_us","GOOG_us","MSFT_us","NFLX_us","NVDA_us","AAPL_us","TSLA_us"]

#set length of data history
num_bars = 250

#set up the shape of the data structure to store prices 
data = np.zeros((num_bars,len(Symbols)))
prices = pd.DataFrame(data,columns=Symbols)

#fill prices dataframe with close prices
for symbol in Symbols:
    prices[symbol]=[rate[4]  for rate in mt5.copy_rates_from(symbol,mt5.TIMEFRAME_D1,startdate,num_bars)]
    
#we donot need mt5 from here 
mt5.shutdown()

#generate pairs from Symbols list 
pairs = list(combinations(prices.columns,2))

#set our desired significance level, 0.01->99%, 0.05->95%, 0.1->90%
confidence_level = 0.1

#do the test for cointegration on each pair and print results
for pair in pairs:
    df=prices[list(pair)]
    adf_stat,pvalue,critvalues=coint(df.values[:,0],df.values[:,1])
    if pvalue < confidence_level:
        print(pair[0]," and ",pair[1], " are likely cointegrated")
    else:
        print(pair[0]," and ",pair[1], " are likely not cointegrated")   

Python-Ergebnisse

MR      0       18:35:17.835    SymbolCointegration (NFLX_us,Daily)     FB_us  and  GOOG_us  are likely not cointegrated
GE      0       18:35:17.851    SymbolCointegration (NFLX_us,Daily)     FB_us  and  MSFT_us  are likely not cointegrated
DI      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NFLX_us  are likely not cointegrated
CJ      0       18:35:17.867    SymbolCointegration (NFLX_us,Daily)     FB_us  and  NVDA_us  are likely not cointegrated
MO      0       18:35:17.882    SymbolCointegration (NFLX_us,Daily)     FB_us  and  AAPL_us  are likely not cointegrated
JQ      0       18:35:17.898    SymbolCointegration (NFLX_us,Daily)     FB_us  and  TSLA_us  are likely not cointegrated
CD      0       18:35:17.914    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  MSFT_us  are likely not cointegrated
MF      0       18:35:17.930    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NFLX_us  are likely not cointegrated
QK      0       18:35:17.946    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  NVDA_us  are likely not cointegrated
HM      0       18:35:17.962    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  AAPL_us  are likely not cointegrated
OO      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     GOOG_us  and  TSLA_us  are likely not cointegrated
MS      0       18:35:17.978    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NFLX_us  are likely not cointegrated
PD      0       18:35:17.994    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  NVDA_us  are likely not cointegrated
MF      0       18:35:18.010    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  AAPL_us  are likely not cointegrated
RJ      0       18:35:18.042    SymbolCointegration (NFLX_us,Daily)     MSFT_us  and  TSLA_us  are likely not cointegrated
RM      0       18:35:18.058    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  NVDA_us  are likely not cointegrated
GP      0       18:35:18.074    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  AAPL_us  are likely not cointegrated
LN      0       18:35:18.089    SymbolCointegration (NFLX_us,Daily)     NFLX_us  and  TSLA_us  are likely cointegrated
EF      0       18:35:18.105    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  AAPL_us  are likely not cointegrated
QI      0       18:35:18.121    SymbolCointegration (NFLX_us,Daily)     NVDA_us  and  TSLA_us  are likely not cointegrated
OJ      0       18:35:18.137    SymbolCointegration (NFLX_us,Daily)     AAPL_us  and  TSLA_us  are likely not cointegrated

Schlussfolgerung

Bisher haben wir uns die Implementierung des Augmented Dickey-Fuller-Tests in MQL5 angesehen und ihn zur Durchführung des Engle-Granger-Tests auf Kointegration verwendet. Der ADF-Test ist ein wichtiges Instrument für diejenigen, die an der Erforschung von Handelsstrategien von Währungspaaren oder statistischer Arbitrage interessiert sind.  Der gesamte in diesem Artikel beschriebene Code ist in der Zip-Datei enthalten. In der nachstehenden Tabelle ist der gesamte Inhalt dieser Datei aufgeführt.

Datei	Beschreibung
Mql5\include\OLS.mqh	Enthält die Definition der OLS-Klasse, die die Regression der gewöhnlichen kleinsten Quadrate implementiert
Mql5\include\ADF.mqh	Enthält die Definition von verschiedenen Funktionen und die CAdf-Klasse, die den ADF-Test implementiert
Mql5\include\CointegrationTest.mqh	Definiert die Klasse CCoint, die einen Kointegrationstest unter Verwendung der Augmented Engle-Granger-Technik implementiert
Mql5\scripts\ADF_test.mq5	Dies ist das MQL5-Skript, das zum Testen der MQL5-Implementierung des ADF-Tests verwendet wird
Mql5\scripts\SymbolCointegrationTester.mq5	Skript zum Testen von Symbolen in MetaTrader 5 auf Kointegration
Mql5\scripts\Test_adfuller.py	Ist ein Python-Skript, das die statsmodels-Implementierung des ADF-Tests verwendet, um unsere MQL5-Implementierung zu validieren
Mql5\scripts\SymbolCointegration.py	Python-Version von SymbolCointegrationTester