文章 "群体优化算法：螺旋动态优化 (SDO) 算法"
再次感谢您提供了另一种算法！
最好能突出重点。
我想征求社区的意见。
其他令人惊叹的算法还在等待轮到它们，对比表变得太大，不方便查看和分析，我想把最弱的算法从表中剔除，但另一方面，我也不想忽略它们。
另外，也许我还可以做一些其他的可视化工作。
总之，我很高兴听到您的意见和建议。
我希望我的文章能成为交易者的思想源泉和灵感之源，能帮助他们用全新的眼光看待普通事物，也能帮助他们在寻找复杂的相互关系时选择合适的工具，帮助他们实现目标并取得新的令人印象深刻的成功。
是的，条形图（直方图）是显示比较内容的好方法，这没有问题。
我的意思是，除了一般的直方图之外，也许还值得为每项测试（共有 9 项测试）分别提供直方图。彩色表格很好，可以让您清楚地识别每个算法的具体情况，但它无法让您了解不同学科之间的差异程度。
而且，虽然我只引用了诚实的算法（即使有些算法不诚实，它们也会被重新修改），但仍有一些算法可以利用测试功能中的可重复性作为 "武器"。
我最近就遇到了这样一种算法，作者使用了在 Rastrigin 函数上搜索最小值的方法，但可以绝对肯定的是，最小值球位于[0,0]（函数定义区域的正中心），这样的算法会带来想象中的 "酷感"。
这就是为什么我正在研究修改测试方法的原因，以消除多维空间中二维函数的重复，同时保留测试过程可视化的可能性--乍看起来，这是一个非常困难的问题。
安德烈，你从哪里得到这个的？
这是你心中的疑问。
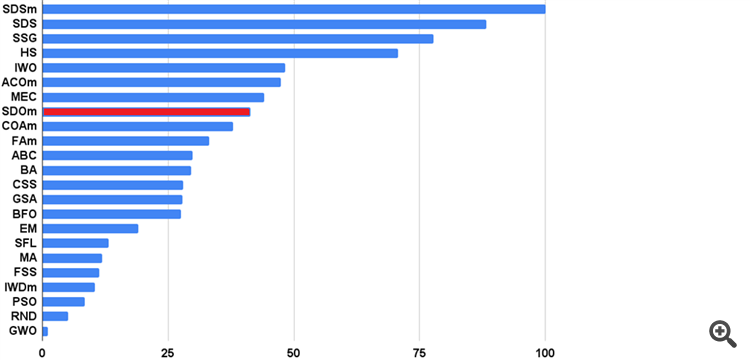
新文章 群体优化算法：螺旋动态优化 (SDO) 算法已发布：
文章介绍了一种基于自然界螺旋轨迹构造模式（如软体动物贝壳）的优化算法 - 螺旋动力学优化算法（Spiral Dynamics Optimization，SDO）。我对作者提出的算法进行了彻底的修改和完善，本文将探讨这些修改的必要性。
螺旋动力学优化（Spiral Dynamics Optimization，SDO）是由 Tamura 和 Yasuda 于 2011 年提出的最简单的物理算法之一，它是利用自然界中的对数螺旋现象而开发的。算法简单，控制参数少。此外，该算法还具有计算速度快、局部搜索能力强、前期多样化和后期强化等特点。
自然界中有许多螺旋，如星系、极光、动物角、龙卷风、贝壳、蜗牛、氨虫、变色龙尾巴或海马。在人类诞生之初创造的古代艺术中也能看到螺旋。多年来，一些研究人员努力了解螺旋序列和复杂性，并开发出螺旋方程和算法。自然界中经常出现的螺旋现象是在星系和热带气旋中观察到的对数螺旋。离散对数螺旋生成过程作为元启发式算法中的高效搜索行为来实现，这为螺旋动力学优化算法的开发提供了灵感。
可见螺旋序列图案在自然界中可以找到很多代表，例如植物、树木、波浪和许多其他形状。自然界中的视觉模式可以用混沌理论、分形、螺旋和其他数学概念来建模。在一些自然形态中，螺旋和分形密切相关。例如，斐波那契螺旋是基于黄金分割率和斐波那契数字的对数螺旋的变体。由于它是对数曲线，因此在每个尺度上看起来都是一样的，也可以被视为分形。
作者：Andrey Dik